🏆 第 313 场力扣周赛

两周没打，感觉又回来了
第二次拿到周赛奖品！

6192. 公因子的数目

给你两个正整数 a 和 b ，返回 a 和 b 的 公 因子的数目。
如果 x 可以同时整除 a 和 b ，则认为 x 是 a 和 b 的一个 公因子 。

示例 1：
输入：a = 12, b = 6 输出：4 解释：12 和 6 的公因子是 1、2、3、6 。
示例 2：
输入：a = 25, b = 30 输出：2 解释：25 和 30 的公因子是 1、5 。

提示：

• 1 <= a, b <= 1000

思路：
暴力：

class Solution {
    public int commonFactors(int a, int b) {
        int c = 0;
        for (int i = 1; i <= Math.min(a, b); i++)
            if (a % i == 0 && b % i == 0)
                c++;
        return c;
    }
}

6193. 沙漏的最大总和

给你一个大小为 m x n 的整数矩阵 grid 。
按以下形式将矩阵的一部分定义为一个 沙漏 ：
返回沙漏中元素的 最大 总和。
注意：沙漏无法旋转且必须整个包含在矩阵中。

示例 1：
输入：grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]] 输出：30 解释：上图中的单元格表示元素总和最大的沙漏：6 + 2 + 1 + 2 + 9 + 2 + 8 = 30 。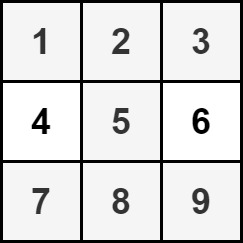

示例 2：
输入：grid = [[1,2,3],[4,5,6],[7,8,9]] 输出：35 解释：上图中的单元格表示元素总和最大的沙漏：1 + 2 + 3 + 5 + 7 + 8 + 9 = 35 。

提示：

• m == grid.length
• n == grid[i].length
• 3 <= m, n <= 150
• 0 <= grid[i][j] <= 106

思路：
暴力计算

class Solution {
    public int maxSum(int[][] g) {
        int max = 0;
        int n = g.length, m = g[0].length;
        for (int i = 1; i < n - 1; i++) {
            for (int j = 1; j < m - 1; j++) {
                int s = 0;
                for (int r = j - 1; r <= j + 1; r++)
                    s += g[i - 1][r] + g[i + 1][r];
                s += g[i][j];
                max = Math.max(max, s);
            }
        }
        return max;
    }
}

6194. 最小 XOR

给你两个正整数 num1 和 num2 ，找出满足下述条件的整数 x ：

• x 的置位数和 num2 相同，且
• x XOR num1 的值 最小

注意 XOR 是按位异或运算。
返回整数_ _x 。题目保证，对于生成的测试用例， x 是 唯一确定 的。
整数的 置位数 是其二进制表示中 1 的数目。

示例 1：
输入：num1 = 3, num2 = 5 输出：3 解释： num1 和 num2 的二进制表示分别是 0011 和 0101 。 整数 3 的置位数与 num2 相同，且 3 XOR 3 = 0 是最小的。
示例 2：
输入：num1 = 1, num2 = 12 输出：3 解释： num1 和 num2 的二进制表示分别是 0001 和 1100 。 整数 3 的置位数与 num2 相同，且 3 XOR 1 = 2 是最小的。

提示：

• 1 <= num1, num2 <= 109

思路：贪心

class Solution {
    public int minimizeXor(int num1, int num2) {
        int c1 = Integer.bitCount(num1), c2 = Integer.bitCount(num2);
        if (c1 == c2) return num1;
        else if (c1 > c2) {
            int x = num1;
            int t = c1 - c2;
            int i = 0;
            while (t > 0) {
                if ((x >> i & 1) == 1) {
                    x ^= 1 << i;
                    t--;
                }
                i++;
            }
            return x;
        } else {
            int x = num1;
            int t = c2 - c1;
            int i = 0;
            while (t > 0) {
                if ((x >> i & 1) == 0) {
                    x ^= 1 << i;
                    t--;
                }
                i++;
            }
            return x;
        }
    }
}

6195. 对字母串可执行的最大删除数

给你一个仅由小写英文字母组成的字符串 s 。在一步操作中，你可以：

• 删除 整个字符串 s ，或者
• 对于满足 1 <= i <= s.length / 2 的任意 i ，如果 s 中的 前 i 个字母和接下来的 i 个字母 相等 ，删除 前 i 个字母。

例如，如果 s = “ababc” ，那么在一步操作中，你可以删除 s 的前两个字母得到 “abc” ，因为 s 的前两个字母和接下来的两个字母都等于 “ab” 。
返回删除 s 所需的最大操作数。

示例 1：
输入：s = “abcabcdabc” 输出：2 解释： - 删除前 3 个字母（”abc”），因为它们和接下来 3 个字母相等。现在，s = “abcdabc”。 - 删除全部字母。 一共用了 2 步操作，所以返回 2 。可以证明 2 是所需的最大操作数。 注意，在第二步操作中无法再次删除 “abc” ，因为 “abc” 的下一次出现并不是位于接下来的 3 个字母。
示例 2：
输入：s = “aaabaab” 输出：4 解释： - 删除第一个字母（”a”），因为它和接下来的字母相等。现在，s = “aabaab”。 - 删除前 3 个字母（”aab”），因为它们和接下来 3 个字母相等。现在，s = “aab”。 - 删除第一个字母（”a”），因为它和接下来的字母相等。现在，s = “ab”。 - 删除全部字母。 一共用了 4 步操作，所以返回 4 。可以证明 4 是所需的最大操作数。
示例 3：
输入：s = “aaaaa” 输出：5 解释：在每一步操作中，都可以仅删除 s 的第一个字母。

提示：

• 1 <= s.length <= 4000
• s 仅由小写英文字母组成

思路：哈希 + DP

class Solution {
    int N = 4010;
    long[] h = new long[N], p = new long[N];
    long P = 13331;
    public int deleteString(String s) {
        char[] a = s.toCharArray();
        int n = a.length;
        p[0] = 1;
        for (int i = 1; i <= n; i++) {
            p[i] = p[i - 1] * P;
            h[i] = h[i - 1] * P + a[i - 1];
        }
        int[] f = new int[n + 1];
        f[n] = 1;
        for (int i = n - 1; i >= 1; i--) {
            f[i] = 1;
            for (int j = i + 1; j <= n; j++) {
                if (j - i > n + 1 - j) break;
                if (get(i, j - 1) == get(j, j + j - 1 - i))
                    f[i] = Math.max(f[i], f[j] + 1);
            }
        }
        return f[1];
    }
    long get(int l, int r) {
        return h[r] - h[l - 1] * p[r - l + 1];
    }
}