周赛 - 🏆 第 270 场力扣周赛 - 《学习笔记》

t4不会，听说是欧拉回路，得补一下知识点！
t3wrong了一次，因为建图的边没开够空间！

5942. 找出 3 位偶数

给你一个整数数组 digits ，其中每个元素是一个数字（0 - 9）。数组中可能存在重复元素。
你需要找出所有满足下述条件且 互不相同 的整数：

该整数由 digits 中的三个元素按任意顺序 依次连接 组成。
该整数不含 前导零
该整数是一个偶数

例如，给定的 digits 是 [1, 2, 3] ，整数 132 和 312 满足上面列出的全部条件。
将找出的所有互不相同的整数按 递增顺序 排列，并以数组形式返回。

示例 1：
输入：digits = [2,1,3,0] 输出：[102,120,130,132,210,230,302,310,312,320] 解释： 所有满足题目条件的整数都在输出数组中列出。注意，答案数组中不含有奇数或带 前导零 的整数。
示例 2：
输入：digits = [2,2,8,8,2] 输出：[222,228,282,288,822,828,882] 解释： 同样的数字（0 - 9）在构造整数时可以重复多次，重复次数最多与其在 digits 中出现的次数一样。在这个例子中，数字 8 在构造 288、828 和 882 时都重复了两次。
示例 3：
输入：digits = [3,7,5] 输出：[] 解释： 使用给定的 digits 无法构造偶数。
示例 4：
输入：digits = [0,2,0,0] 输出：[200] 解释： 唯一一个不含 前导零 且满足全部条件的整数是 200 。
示例 5：
输入：digits = [0,0,0] 输出：[] 解释： 构造的所有整数都会有 前导零 。因此，不存在满足题目条件的整数。

提示：

3 <= digits.length <= 100
0 <= digits[i] <= 9

思路：
暴力三重循环 + Set去重

class Solution {
    public int[] findEvenNumbers(int[] d) {
        Set<Integer> set = new HashSet<>();
        int n = d.length;
        for (int i = 0; i < n; i++) {
            if (d[i] == 0) continue;
            for (int j = 0; j < n; j++) {
                if (j == i) continue;
                for (int k = 0; k < n; k++) {
                    if (k == i || k == j || d[k] % 2 != 0)
                        continue;
                    set.add(d[i] * 100 + d[j] * 10 + d[k]);
                }
            }
        }
        int[] res = new int[set.size()];
        int idx = 0;
        for (int x : set)
            res[idx++] = x;
        Arrays.sort(res);
        return res;
    }
}

5943. 删除链表的中间节点

给你一个链表的头节点 head 。删除链表的 中间节点 ，并返回修改后的链表的头节点 head 。
长度为 n 链表的中间节点是从头数起第 ⌊n / 2⌋ 个节点（下标从 0 开始），其中 ⌊x⌋ 表示小于或等于 x 的最大整数。

对于 n = 1、2、3、4 和 5 的情况，中间节点的下标分别是 0、1、1、2 和 2 。

示例 1：

输入：head = [1,3,4,7,1,2,6] 输出：[1,3,4,1,2,6] 解释： 上图表示给出的链表。节点的下标分别标注在每个节点的下方。由于 n = 7 ，值为 7 的节点 3 是中间节点，用红色标注。返回结果为移除节点后的新链表。
示例 2：

输入：head = [1,2,3,4] 输出：[1,2,4] 解释： 上图表示给出的链表。对于 n = 4 ，值为 3 的节点 2 是中间节点，用红色标注。
示例 3：

输入：head = [2,1] 输出：[2] 解释： 上图表示给出的链表。对于 n = 2 ，值为 1 的节点 1 是中间节点，用红色标注。值为 2 的节点 0 是移除节点 1 后剩下的唯一一个节点。

提示：

链表中节点的数目在范围 [1, 105] 内
1 <= Node.val <= 105

思路：快慢指针

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode deleteMiddle(ListNode head) {
        if (head == null || head.next == null)
            return null;
        ListNode fast = head, slow = head, pre = null;
        do {
            pre = slow;
            fast = fast.next.next;
            slow = slow.next;
        } while (fast != null && fast.next != null);
        pre.next = pre.next == null ? null : pre.next.next;
        return head;
    }
}

5944. 从二叉树一个节点到另一个节点每一步的方向

给你一棵 二叉树 的根节点 root ，这棵二叉树总共有 n 个节点。每个节点的值为 1 到 n 中的一个整数，且互不相同。给你一个整数 startValue ，表示起点节点 s 的值，和另一个不同的整数 destValue ，表示终点节点 t 的值。
请找到从节点 s 到节点 t 的 最短路径 ，并以字符串的形式返回每一步的方向。每一步用大写字母 ‘L’ ，’R’ 和 ‘U’ 分别表示一种方向：

‘L’ 表示从一个节点前往它的 左孩子 节点。
‘R’ 表示从一个节点前往它的 右孩子 节点。
‘U’ 表示从一个节点前往它的父节点。

请你返回从 s 到 t 最短路径 每一步的方向。

示例 1：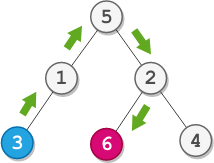

输入：root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6 输出：“UURL” 解释：最短路径为：3 → 1 → 5 → 2 → 6 。
示例 2：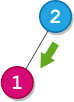

输入：root = [2,1], startValue = 2, destValue = 1 输出：“L” 解释：最短路径为：2 → 1 。

提示：

树中节点数目为 n 。
2 <= n <= 105
1 <= Node.val <= n
树中所有节点的值 互不相同 。
1 <= startValue, destValue <= n
startValue != destValue

思路：
方法一：
建图 + bfs + 倒推路径
方法二：
利用最近公共祖先的性质，起点到终点一定经过其最近公共祖先。
找到从根节点分别到起点和终点的路径，去除其公共前缀，将到起点的剩余部分全换成’U’，再连上到终点的剩余部分即可！。

// 方法一：
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int N = 100010;
    int[] h = new int[N], e = new int[2 * N], ne = new int[2 * N];
    char[] w = new char[2 * N];
    int idx;
    int[] pre = new int[N];
    char[] cp = new char[N];
    int S, E;
    StringBuilder sb= new StringBuilder();
    public String getDirections(TreeNode root, int S, int E) {
        this.S = S;
        this.E = E;
        Arrays.fill(h, -1);
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        while (!q.isEmpty()) {
            TreeNode cur = q.poll();
            // n++;
            if (cur.left != null) {
                q.offer(cur.left);
                add(cur.val, cur.left.val, 'L');
                add(cur.left.val, cur.val, 'U');
            }
            if (cur.right != null) {
                q.offer(cur.right);
                add(cur.val, cur.right.val, 'R');
                add(cur.right.val, cur.val, 'U');
            }
        }
        Queue<Integer> q2 = new LinkedList<>();
        q2.offer(S);
        boolean[] st = new boolean[N];
        label: while (!q2.isEmpty()) {
            int cur = q2.poll();
            st[cur] = true;
            for (int i = h[cur]; i != -1; i = ne[i]) {
                int j = e[i];
                if (st[j]) continue;
                q2.offer(j);
                pre[j] = cur;
                cp[j] = w[i];
                if (j == E)
                    break label;
            }
        }
        // System.out.println(Arrays.toString(pre));
        dfs(E);
        return sb.reverse().toString();
    }
    void dfs(int cur) {
        if (cur == S) {
            return;
        }
        sb.append(cp[cur]);
        dfs(pre[cur]);
    }
    void add(int a, int b, char c) {
        e[idx] = b;
        w[idx] = c;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}

// 方法二
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    StringBuilder sbs = new StringBuilder();
    StringBuilder sbe = new StringBuilder();
    public String getDirections(TreeNode root, int startValue, int destValue) {
        dfs(root, startValue, true);
        dfs(root, destValue, false);
        System.out.println(sbs);
        System.out.println(sbe);
        int j = -1;
        for (int i = 0; i < Math.min(sbs.length(), sbe.length()); i++) {
            if (sbs.charAt(i) != sbe.charAt(i)) {
                j = i;
                break;
            }
        }
        if (j == -1)
            j = Math.min(sbs.length(), sbe.length());
        sbs = new StringBuilder(sbs.substring(j, sbs.length()));
        String s = sbe.substring(j, sbe.length());
        for (int i = 0; i < sbs.length(); i++)
            sbs.setCharAt(i, 'U');
        sbs.append(s);
        return sbs.toString();
    }
    boolean dfs(TreeNode root , int x, boolean flag) {
        StringBuilder sb = flag ? sbs : sbe;
        if (root == null) return false;
        if (root.val == x) return true;
        sb.append('L');
        if (dfs(root.left, x, flag))
            return true;
        sb.deleteCharAt(sb.length() - 1);
        sb.append('R');
        if (dfs(root.right, x, flag))
            return true;
        sb.deleteCharAt(sb.length() - 1);
        return false;
    }
}

5932. 合法重新排列数对

给你一个下标从 0 开始的二维整数数组 pairs ，其中 pairs[i] = [starti, endi] 。如果 pairs 的一个重新排列，满足对每一个下标 i （ 1 <= i < pairs.length ）都有 endi-1 == starti ，那么我们就认为这个重新排列是 pairs 的一个 合法重新排列 。
请你返回 任意一个 pairs 的合法重新排列。
注意：数据保证至少存在一个 pairs 的合法重新排列。

示例 1：
输入：pairs = [[5,1],[4,5],[11,9],[9,4]] 输出：[[11,9],[9,4],[4,5],[5,1]] 解释： 输出的是一个合法重新排列，因为每一个 endi-1 都等于 starti 。 end0 = 9 == 9 = start1 end1 = 4 == 4 = start2 end2 = 5 == 5 = start3
示例 2：
输入：pairs = [[1,3],[3,2],[2,1]] 输出：[[1,3],[3,2],[2,1]] 解释： 输出的是一个合法重新排列，因为每一个 endi-1 都等于 starti 。 end0 = 3 == 3 = start1 end1 = 2 == 2 = start2 重新排列后的数组 [[2,1],[1,3],[3,2]] 和 [[3,2],[2,1],[1,3]] 都是合法的。
示例 3：
输入：pairs = [[1,2],[1,3],[2,1]] 输出：[[1,2],[2,1],[1,3]] 解释： 输出的是一个合法重新排列，因为每一个 endi-1 都等于 starti 。 end0 = 2 == 2 = start1 end1 = 1 == 1 = start2

提示：

1 <= pairs.length <= 105
pairs[i].length == 2
0 <= starti, endi <= 109
starti != endi
pairs 中不存在一模一样的数对。
至少存在一个合法的pairs 重新排列。

思路：
欧拉通路，本题给定了条件，一定存在欧拉通路。
如果没有给定，如何判断呢？
如果是无向图，欧拉通路需满足奇度节点的个数为0或2，其余均为偶度节点
如果是无向图，欧拉通路需满足，所有点的入度等于出度，或者有且只有一点出度比入度大1，有且只有一点入度比出度大1，其余节点入度与出度均相等。
另一个问题是如何求解欧拉通路，即如何求出一笔画的路线呢？
用递归，从起点出发，一条道走到黑再向回倒退，一旦能向前走则继续一条道走到黑，直至遍历完所有的边

class Solution {
    Map<Integer, Queue<Integer>> map = new HashMap<>();
    List<int[]> t = new ArrayList<>();
    public int[][] validArrangement(int[][] pairs) {
        for (int[] p : pairs) {
            int a = p[0], b = p[1];
            map.computeIfAbsent(a, key -> new LinkedList<>()).offer(b);
        }
        Map<Integer, Integer> in = new HashMap<>();
        Map<Integer, Integer> out = new HashMap<>();
        for (Integer key : map.keySet()) {
            Queue<Integer> list = map.get(key);
            out.merge(key, list.size(), Integer::sum);
            for (int x : list) {
                in.merge(x, 1, Integer::sum);
            }
        }
        int start = -1;
        for (int key : out.keySet()) {
            int din = in.getOrDefault(key, 0);
            int dout = out.get(key);
            if (din + 1 == dout) {
                start = key;
                break;
            }
        }
        if (start == -1) {
            start = pairs[0][0];
        }
        dfs(start);
        int[][] res = new int[t.size()][2];
        for (int i = 0, j = t.size() - 1; j >= 0; i++, j--) {
            res[i] = t.get(j);
        }
        return res;
    }
    //欧拉通路的精髓
    void dfs(int u) {
        Queue<Integer> q = map.get(u);
        if (q == null) return;
        while (!q.isEmpty()) {
            int v = q.poll();
            dfs(v);
            t.add(new int[]{u, v});
        }
    }
}