96. 不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：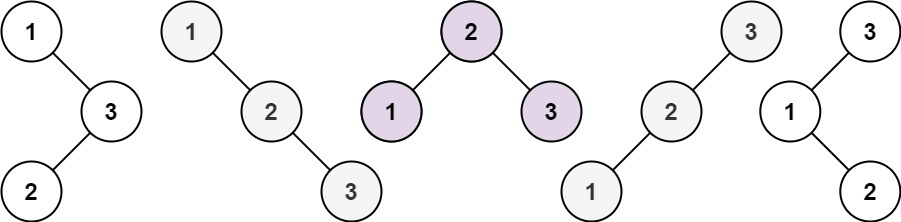
二叉搜索树 - 图1
输入：n = 3
输出：5

示例 2：
输入：n = 1
输出：1


提示：

  • 1 <= n <= 19

思路：
线性DP

  1. class Solution {
  2.     public int numTrees(int n) {
  3.         int[] f = new int[n + 1];
  4.         f[0] = f[1] = 1;
  6.         for (int i = 2; i <= n; i++) {
  7.             for (int j = 1; j <= i; j++) {
  8.                 f[i] += f[j - 1] * f[i - j];
  9.             }
  10.         }
  11.         return f[n];
  12.     }
  13. }

108. 将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：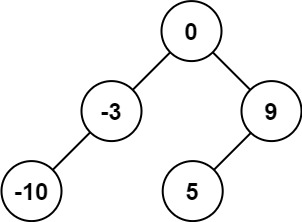
二叉搜索树 - 图2输入：nums = [-10,-3,0,5,9]输出：[0,-3,9,-10,null,5]解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案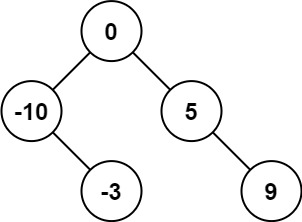：二叉搜索树 - 图3
示例 2：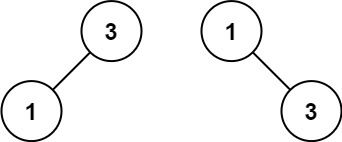
二叉搜索树 - 图4
输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。


提示：

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 按 严格递增 顺序排列

思路：递归自上而下建立整棵树即可！

  1. /**
  2.  * Definition for a binary tree node.
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode() {}
  8.  *     TreeNode(int val) { this.val = val; }
  9.  *     TreeNode(int val, TreeNode left, TreeNode right) {
  10.  *         this.val = val;
  11.  *         this.left = left;
  12.  *         this.right = right;
  13.  *     }
  14.  * }
  15.  */
  16. class Solution {
  17.     public TreeNode sortedArrayToBST(int[] nums) {
  18.         int n = nums.length;
  19.         if (n == 0)
  20.             return null;
  21.         TreeNode root = new TreeNode(nums[n / 2]);
  22.         root.left = dfs(nums, 0, n / 2 - 1);
  23.         root.right = dfs(nums, n / 2 + 1, n - 1);
  24.         return root;
  25.     }
  27.     TreeNode dfs(int[] nums, int l, int r) {
  28.         if (l > r)
  29.             return null;
  30.         int mid = l + r >> 1;
  31.         TreeNode cur = new TreeNode(nums[mid]);
  32.         cur.left = dfs(nums, l, mid - 1);
  33.         cur.right = dfs(nums, mid + 1, r);
  34.         return cur;
  35.     }
  36. }

109. 有序链表转换二叉搜索树

给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。
本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
给定的有序链表： [-10, -3, 0, 5, 9],
一个可能的答案是：[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树：
0
/ \
-3 9
/ /
-10 5

思路：

  1. 遍历一遍链表得到长度
  2. 用108的方法建一棵空树
  3. 中序遍历填充每个节点

巧妙选择遍历方案避免链表不能随机访问的缺点！

  1. /**
  2.  * Definition for singly-linked list.
  3.  * public class ListNode {
  4.  *     int val;
  5.  *     ListNode next;
  6.  *     ListNode() {}
  7.  *     ListNode(int val) { this.val = val; }
  8.  *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
  9.  * }
  10.  */
  11. /**
  12.  * Definition for a binary tree node.
  13.  * public class TreeNode {
  14.  *     int val;
  15.  *     TreeNode left;
  16.  *     TreeNode right;
  17.  *     TreeNode() {}
  18.  *     TreeNode(int val) { this.val = val; }
  19.  *     TreeNode(int val, TreeNode left, TreeNode right) {
  20.  *         this.val = val;
  21.  *         this.left = left;
  22.  *         this.right = right;
  23.  *     }
  24.  * }
  25.  */
  26. class Solution {
  27.     ListNode gg;
  28.     public TreeNode sortedListToBST(ListNode head) {
  29.         ListNode cur = head;
  30.         gg = head;
  31.         int len = 0;
  32.         while (cur != null) {
  33.             cur = cur.next;
  34.             len++;
  35.         }
  36.         // System.out.println(len);
  37.         TreeNode root = dfs1(0, len - 1);
  38.         dfs2(root);
  39.         return root;
  40.     }
  41.     TreeNode dfs1(int l, int r) {
  42.         if (l > r)
  43.             return null;
  44.         int mid = l + r >> 1;
  45.         TreeNode cur = new TreeNode();
  46.         cur.left = dfs1(l, mid - 1);
  47.         cur.right = dfs1(mid + 1, r);
  48.         return cur;
  49.     }
  50.     void dfs2(TreeNode root) {
  51.         if (root == null)
  52.             return;
  53.         dfs2(root.left);
  54.         root.val = gg.val;
  55.         gg = gg.next;
  56.         dfs2(root.right);
  57.     }
  58. }

95. 不同的二叉搜索树 II

难度中等1024收藏分享切换为英文接收动态反馈
给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例 1：
二叉搜索树 - 图5
输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

示例 2：
输入：n = 1
输出：[[1]]


提示：

  • 1 <= n <= 8

思路：
在96的基础上，不问个数，而是要求输出每一种情况的根节点构成的链表
也用到了108的类似转换方法
我当时的问题：怎么递归保存所有的结果？
是我太年轻了，还是得再暴力一点才能做出来
对于每个根节点来说，生成它的左右子树的所有情况并做拼接

  1. /**
  2.  * Definition for a binary tree node.
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode() {}
  8.  *     TreeNode(int val) { this.val = val; }
  9.  *     TreeNode(int val, TreeNode left, TreeNode right) {
  10.  *         this.val = val;
  11.  *         this.left = left;
  12.  *         this.right = right;
  13.  *     }
  14.  * }
  15.  */
  16. class Solution {
  17.     public List<TreeNode> generateTrees(int n) {
  18.         return dfs(1, n);
  19.     }
  20.     List<TreeNode> dfs(int l, int r) {
  21.         if (l > r) {
  22.             List<TreeNode> res = new ArrayList<>();
  23.             res.add(null);
  24.             return res;
  25.         }
  26.         List<TreeNode> res = new ArrayList<>();
  27.         for (int i = l; i <= r; i++) {
  28.             List<TreeNode> ll = dfs(l, i - 1);
  29.             List<TreeNode> rr = dfs(i + 1, r);
  30.             for (TreeNode lo : ll) {
  31.                 for (TreeNode ro : rr) {
  32.                     TreeNode root = new TreeNode(i, lo, ro);
  33.                     res.add(root);
  34.                 }
  35.             }
  36.         }
  37.         return res;
  38.     }
  39. }

剑指 Offer 36. 二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

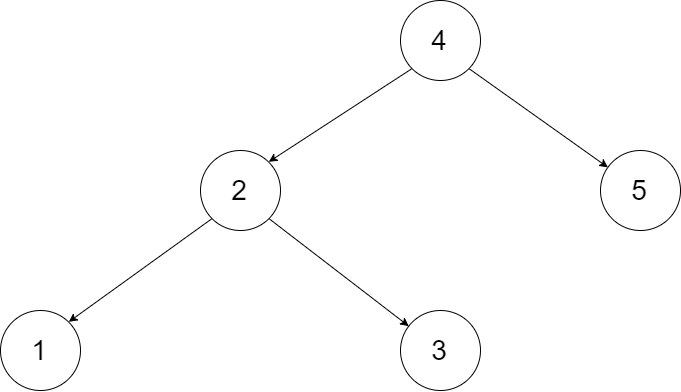
二叉搜索树 - 图6

我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
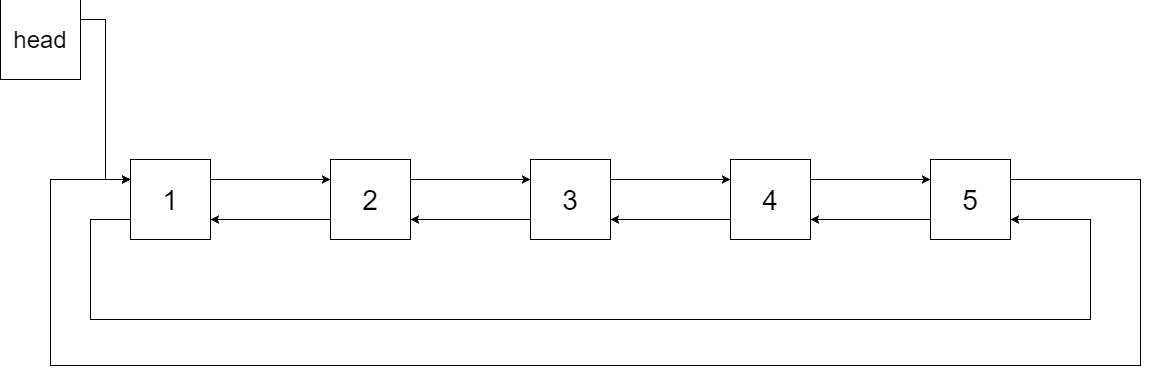
image.png


特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

思路：
先序遍历，不要被二叉搜索树的中序遍历给干扰！
递归得到当前根节点左右子树的双向链表，再将根节点合并到双向链表中！

  1. /*
  2. // Definition for a Node.
  3. class Node {
  4.     public int val;
  5.     public Node left;
  6.     public Node right;
  8.     public Node() {}
  10.     public Node(int _val) {
  11.         val = _val;
  12.     }
  14.     public Node(int _val,Node _left,Node _right) {
  15.         val = _val;
  16.         left = _left;
  17.         right = _right;
  18.     }
  19. };
  20. */
  21. class Solution {
  22.     public Node treeToDoublyList(Node root) {
  23.         if (root == null)
  24.             return null;
  25.         Pair p = dfs(root);
  26.         p.left.left = p.right;
  27.         p.right.right = p.left;
  28.         return p.left;
  29.     }
  30.     Pair dfs(Node root) {
  31.         if (root.left == null && root.right == null)
  32.             return new Pair(root, root);
  33.         else if (root.left != null && root.right != null) {
  34.             Pair p = dfs(root.left);
  35.             Pair q = dfs(root.right);
  36.             p.right.right = root;
  37.             root.left = p.right;
  38.             q.left.left = root;
  39.             root.right = q.left;
  40.             return new Pair(p.left, q.right);
  41.         } else if (root.left != null) {
  42.             Pair p = dfs(root.left);
  43.             p.right.right = root;
  44.             root.left = p.right;
  45.             return new Pair(p.left, root);
  46.         } else {
  47.             Pair q = dfs(root.right);
  48.             q.left.left = root;
  49.             root.right = q.left;
  50.             return new Pair(root, q.right);
  51.         }
  52.     }
  53. }
  54. class Pair {
  55.     Node left, right;
  56.     Pair(Node left, Node right) {
  57.         this.left = left;
  58.         this.right = right;
  59.     }
  60. }

98. 验证二叉搜索树（判断一棵树是否为二叉搜索树）

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：

  • 节点的左子树只包含 小于 当前节点的数。
  • 节点的右子树只包含 大于 当前节点的数。

  • 所有左子树和右子树自身必须也是二叉搜索树。


    示例 1：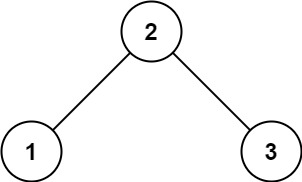
    二叉搜索树 - 图8
    输入：root = [2,1,3]
    输出：true

示例 2：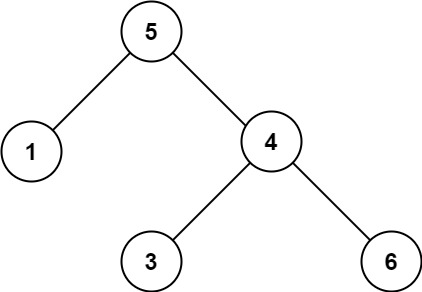
二叉搜索树 - 图9
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。


提示：

  • 树中节点数目范围在[1, 104] 内
  • -231 <= Node.val <= 231 - 1
  1. /**
  2.  * Definition for a binary tree node.
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode() {}
  8.  *     TreeNode(int val) { this.val = val; }
  9.  *     TreeNode(int val, TreeNode left, TreeNode right) {
  10.  *         this.val = val;
  11.  *         this.left = left;
  12.  *         this.right = right;
  13.  *     }
  14.  * }
  15.  */
  16. class Solution {
  17.     long min = Long.MIN_VALUE;
  18.     public boolean isValidBST(TreeNode root) {
  19.         return dfs(root);
  20.     }
  21.     boolean dfs(TreeNode root) {
  22.         if (root == null)
  23.             return true;
  24.         if (!dfs(root.left))
  25.             return false;
  27.         if (root.val <= min)
  28.             return false;
  29.         min = root.val;
  30.         return dfs(root.right);
  31.     }
  32. }

173. 二叉搜索树迭代器

实现一个二叉搜索树迭代器类BSTIterator ，表示一个按中序遍历二叉搜索树（BST）的迭代器：

  • BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字，且该数字小于 BST 中的任何元素。
  • boolean hasNext() 如果向指针右侧遍历存在数字，则返回 true ；否则返回 false 。
  • int next()将指针向右移动，然后返回指针处的数字。

注意，指针初始化为一个不存在于 BST 中的数字，所以对 next() 的首次调用将返回 BST 中的最小元素。
你可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 的中序遍历中至少存在一个下一个数字。

示例：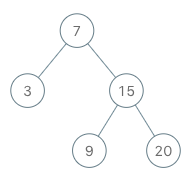
二叉搜索树 - 图10
输入
[“BSTIterator”, “next”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]

解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // 返回 3
bSTIterator.next(); // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 20
bSTIterator.hasNext(); // 返回 False


提示：

  • 树中节点的数目在范围 [1, 105] 内
  • 0 <= Node.val <= 106

  • 最多调用 105 次 hasNext 和 next 操作


    进阶：

  • 你可以设计一个满足下述条件的解决方案吗？next() 和 hasNext() 操作均摊时间复杂度为 O(1) ，并使用 O(h) 内存。其中 h 是树的高度。

思路：
使用自定义栈进行中序遍历

  1. /**
  2.  * Definition for a binary tree node.
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode() {}
  8.  *     TreeNode(int val) { this.val = val; }
  9.  *     TreeNode(int val, TreeNode left, TreeNode right) {
  10.  *         this.val = val;
  11.  *         this.left = left;
  12.  *         this.right = right;
  13.  *     }
  14.  * }
  15.  */
  16. class BSTIterator {
  18.     Deque<TreeNode> stack = new LinkedList<>(); 
  19.     public BSTIterator(TreeNode root) {
  20.         while (root != null) {
  21.             stack.push(root);
  22.             root = root.left;
  23.         }
  24.     }
  26.     public int next() {
  27.         TreeNode cur = stack.pop();
  28.         int x = cur.val;
  29.         if (cur.right != null) {
  30.             cur = cur.right;
  31.             while (cur != null) {
  32.                 stack.push(cur);
  33.                 cur = cur.left;
  34.             }
  35.         }
  36.         return x;
  37.     }
  39.     public boolean hasNext() {
  40.         return !stack.isEmpty();
  41.     }
  42. }
  44. /**
  45.  * Your BSTIterator object will be instantiated and called as such:
  46.  * BSTIterator obj = new BSTIterator(root);
  47.  * int param_1 = obj.next();
  48.  * boolean param_2 = obj.hasNext();
  49.  */

剑指 Offer II 053. 二叉搜索树中的中序后继

给定一棵二叉搜索树和其中的一个节点 p ，找到该节点在树中的中序后继。如果节点没有中序后继，请返回 null 。
节点 p 的后继是值比 p.val 大的节点中键值最小的节点，即按中序遍历的顺序节点 p 的下一个节点。

示例 1：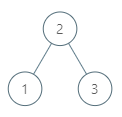
image.png
输入：root = [2,1,3], p = 1 输出：2 解释：这里 1 的中序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。
示例 2：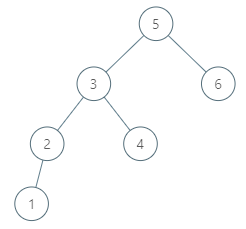
image.png
输入：root = [5,3,6,2,4,null,null,1], p = 6 输出：null 解释：因为给出的节点没有中序后继，所以答案就返回 null 了。

提示：

  • 树中节点的数目在范围 [1, 104] 内。
  • -105 <= Node.val <= 105
  • 树中各节点的值均保证唯一。

思路：
因为是二叉搜索树，所以给定节点的中序后继就是第一个比它节点存的值大的节点。
只需扫描目标节点所在的分支（指一条完整的从根节点到叶节点的路径，其中包括目标节点，如果存在的话）即可找到第一个比他大的节点。

  1. /**
  2.  * Definition for a binary tree node.
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode(int x) { val = x; }
  8.  * }
  9.  */
  10. class Solution {
  11.     public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
  12.         TreeNode ans = null, cur = root;
  13.         while (cur != null) {
  14.             if (cur.val > p.val) {
  15.                 ans = cur;
  16.                 cur = cur.left;
  17.             } else {
  18.                 cur = cur.right;
  19.             }
  20.         }
  21.         return ans;
  22.     }
  23. }

示例：
文稿 2021年12月7日.pdf

普通二叉树的中序后继

思路：
利用中序遍历，记录目标节点是否已经被访问到，若目标节点已经被访问到，则接下来遍历的第一个节点就是其后继

  1. /**
  2.  * Definition for a binary tree node.
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode(int x) { val = x; }
  8.  * }
  9.  */
  10. class Solution {
  11.     TreeNode ans;
  12.     boolean flag;
  13.     public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
  14.         dfs(root, p);
  15.         return ans;
  16.     }
  17.     void dfs(TreeNode root, TreeNode p) {
  18.         if (root == null) return;
  19.         dfs(root.left, p);
  21.         if (flag && ans == null)
  22.             ans = root;
  23.         if (root == p)
  24.             flag = true;
  26.         dfs(root.right, p);
  27.     }
  28. }