刷题记录 - 接雨水 - 《学习笔记》

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：
接雨水 - 图1
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：
输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

思路：

单调栈：考虑每一个可行高度（由每个元素的高度决定）和宽度

维护一个单调递减栈，遍历到当前元素时如果大于栈顶元素说明这两者之间构成了一个凹槽，可以用来蓄水

双指针：考虑每一个位置能存水的最大高度

最大高度取决于左右两边最大高度的最小值。
左右分别维护一个最大值，根据当前左右最大值判断左指针移动还是右指针移动（木桶效应）。

//单调栈
class Solution {
    public int trap(int[] height) {
        Deque<Integer> q = new ArrayDeque<>();
        int ans = 0;
        for (int i = 0; i < height.length; i++) {
            int last = 0;
            while (!q.isEmpty() && height[q.peekLast()] <= height[i]) {
                int j = q.pollLast();
                ans += (height[j] - last) * (i - j - 1);
                last = height[j];
            }
            //如果此时栈中还有元素说明左边高度此时大于右边高度，需要用右边元素来更新
            if (!q.isEmpty())
                ans += (height[i] - last) * (i - q.peekLast() - 1);
            q.offer(i);
        }
        return ans;
    }
}

//双指针
class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int lmax = height[0], rmax = height[n - 1];
        int l = 0, r = n - 1;
        int ans = 0;
        while (l <= r) {
            lmax = Math.max(lmax, height[l]);
            rmax = Math.max(rmax, height[r]);
            if (lmax < rmax) {
                ans += Math.max(0, lmax - height[l]);
                l++;
            } else {
                ans += Math.max(0, rmax - height[r]);
                r--;
            }
        }
        return ans;
    }
}

407. 接雨水 II

给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例 1: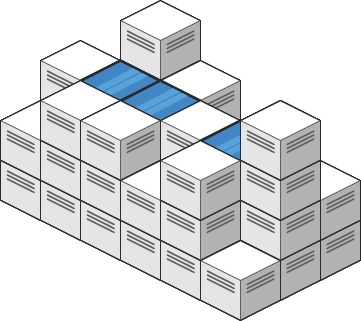
接雨水 - 图2
输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
输出: 4
解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。

示例 2: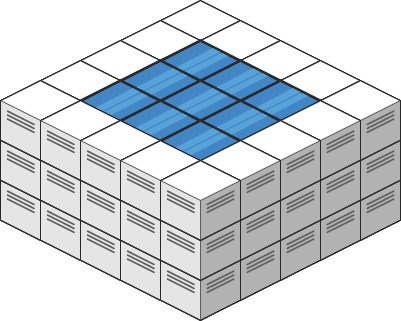
接雨水 - 图3
输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
输出: 10

提示:

m == heightMap.length
n == heightMap[i].length
1 <= m, n <= 200
0 <= heightMap[i][j] <= 2 * 104

思路：
类似于二维的接雨水的双指针做法。
一个位置能存的最大高度等价于在这个位置倒水，直至水流出边界的最大高度
从流出倒推！类似于Dijkstra但不相同。

如果能流出一定是从当前外围一圈的最低高度处流出。

class Solution {
    public int trapRainWater(int[][] h) {
        if (h.length == 0 || h[0].length == 0)
            return 0;
        int n = h.length, m = h[0].length;
        PriorityQueue<Node> q = new PriorityQueue<>((o1, o2) -> o1.val - o2.val);
        boolean[][] st = new boolean[n][m];
        for (int i = 0; i < n; i++) {
            st[i][0] = st[i][m - 1] = true;
            q.offer(new Node(i, 0, h[i][0]));
            q.offer(new Node(i, m - 1, h[i][m - 1]));
        }
        for (int j = 1; j + 1 < m; j++) {
            st[0][j] = st[n - 1][j] = true;
            q.offer(new Node(0, j, h[0][j]));
            q.offer(new Node(n - 1, j, h[n - 1][j]));
        }
        int res = 0;
        int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};
        while (!q.isEmpty()) {
            Node p = q.poll();
            int x = p.x, y = p.y, val = p.val;
            res += val - h[x][y];
            for (int i = 0; i < 4; i++) {
                int a = x + dx[i], b = y + dy[i];
                if (a >= 0 && a < n && b >= 0 && b < m && !st[a][b]) {
                    st[a][b] = true;
                    q.offer(new Node(a, b, Math.max(h[a][b], val)));
                }
            }
        }
        return res;
    }
}
class Node {
    int x, y, val;
    Node (int x, int y, int val) {
        this.x = x;
        this.y = y;
        this.val = val;
    }
}

方法二：并查集
从低向高依次处理每个位置，假设当前正在处理的位置为cur，考虑其四周，若已经被处理过，将cur并入。
考虑cur是否为边界，若是，将其合并到0所在集合，并计算此连通块能存的水量。

class Solution {
    int n, m;
    int[] fa;
    int[] size;
    int[] sum;
    int ans;
    public int trapRainWater(int[][] heightMap) {
        //填块法(并查集)
        n = heightMap.length;
        m = heightMap[0].length;
        fa = new int[n * m + 1];
        size = new int[n * m + 1];
        sum = new int[n * m + 1];
        int[][] a = new int[n * m + 1][3];
        a[0] = new int[]{0, 0, 0};
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                int idx = getIdx(i, j);
                a[idx] = new int[]{heightMap[i][j], i, j};
            }
        }
        Arrays.sort(a, (o1, o2) -> (o1[0] == o2[0] ? getIdx(o1[1], o1[2]) - getIdx(o2[1], o2[2]) : o1[0] - o2[0]));
        int[] dy = {0, 1, 0, -1}, dx = {-1, 0, 1, 0};
        // for (int i = 0; i <= n * m; i++)
        //     System.out.println(Arrays.toString(a[i]));
        for (int i = 1; i <= n * m; i++) {
            int idx = getIdx(a[i][1], a[i][2]);
            fa[idx] = idx;
            size[idx] = 1;
            sum[idx] = a[i][0];
            for (int j = 0; j < 4; j++) {
                int x = a[i][1] + dx[j], y = a[i][2] + dy[j];
                if (x >= 0 && x < n && y >= 0 && y < m && size[getIdx(x, y)] > 0)
                    merge(idx, getIdx(x, y), a[i][0]);
            }
            if (a[i][1] == 0 || a[i][1] == n - 1 || a[i][2] == 0 || a[i][2] == m - 1)
                merge(0, idx, a[i][0]);
        }
        return ans;
    }
    int find(int x) {
        return x == fa[x] ? x : (fa[x] = find(fa[x]));
    }
    void merge(int x, int y, int h) {
        int px = find(x), py = find(y);
        if (px == py) return;
        if (px > py) {
            int t = px;
            px = py;
            py = t;
        }
        fa[py] = px;
        size[px] += size[py];
        sum[px] += sum[py];
        if (px == 0)
            ans += (h * size[py] - sum[py]);
    }
    int getIdx(int i, int j) {
        return i * m + j + 1;
    }
}

关键在在于处理cur时，将其并入四周连通块的集合并查集做法