记忆化搜索 = 深度优先搜索的实现 + 动态规划的思想

1. 步骤

总共可以归纳为以下四步：

  1）合法性剪枝   2）偏序关系剪枝   3）记忆化剪枝   4）递归计算结果并返回 ”

1）合法性剪枝

  • 因为在递归计算的时候，我们必须保证传入参数的合法性，所以这一步是必要的，比如坐标为负数之类的判断；

2）偏序关系剪枝

  • 偏序关系其实就是代表了状态转移的方向，例如【例题2】中，只允许值大的往值小的方向走，这就是一种偏序关系；如果不满足偏序关系的就不能继续往下搜索了；

3）记忆化剪枝

  • 记忆化剪枝就是去对应的哈希数组判断这个状态是否曾经已经计算过，如果计算过则直接返回，时间复杂度 ；

4）递归计算结果并返回

  • 这一步就是深度优先搜索的递归过程，也是递归子问题取最优解的过程，需要具体问题具体分析.

2. 优点

1、忽略边界判断

  • 状态转移的时候完全不需要进行边界判断，只需要在递归调用的出口进行统一判断即可，这样使得代码更加简洁清晰；

2、编码方便

  • 相比动态规划而言，不用去关心子问题的枚举顺序问题，也不用管数组下标越界问题，只要按照深度优先搜索的思路，把代码框架写好，再加入记忆化部分的代码即可，实现方便，手到擒来；

    3. 应用

  1. 没法直接DP，只能记忆化搜索
  2. 路径问题（一维或二维）
  3. 双序列问题

    例题

    不能直接DP

    329. 矩阵中的最长递增路径

    image.png
    给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。
    对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：
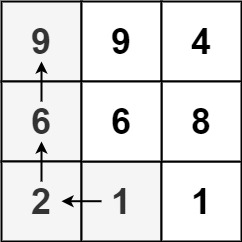
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]] 输出：4 解释：最长递增路径为 [1, 2, 6, 9]。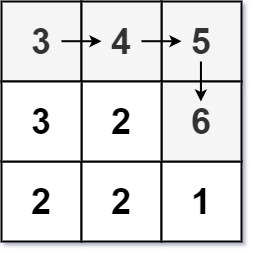
image.png
示例 2：
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]] 输出：4 解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3：
输入：matrix = [[1]] 输出：1

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 200
  • 0 <= matrix[i][j] <= 231 - 1

思路：
DP无法确定求解顺序，故采用记忆化搜索
当然本题用拓扑排序也能做

  1. class Solution {
  2.     int n, m;
  3.     int ans = 0;
  4.     int[][] f;
  5.     public int longestIncreasingPath(int[][] matrix) {
  6.         n = matrix.length;
  7.         m = matrix[0].length;
  8.         f = new int[n][m];
  9.         for (int i = 0; i < n; i++)
  10.             Arrays.fill(f[i], -1);
  11.         for (int i = 0; i < n; i++) {
  12.             for (int j = 0; j < m; j++) {
  13.                 ans = Math.max(ans, dfs(i, j, matrix));
  14.             }
  15.         }
  16.         return ans;
  17.     }
  19.     int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};
  20.     int dfs(int x, int y, int[][] matrix) {
  21.         if (f[x][y] != -1)
  22.             return f[x][y];
  23.         int cnt = 1;
  24.         for (int i = 0; i < 4; i++) {
  25.             int a = x + dx[i], b = y + dy[i];
  26.             if (a < 0 || a >= n || b < 0 || b >= m || matrix[a][b] <= matrix[x][y])
  27.                 continue;
  28.             cnt = Math.max(cnt, dfs(a, b, matrix) + 1);
  29.         }
  31.         return f[x][y] = cnt;
  32.     }
  33. }

Fibonacci 数列


记忆化搜索 - 图3

路径问题

576. 出界的路径数

image.png
给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。你 最多 可以移动 maxMove 次球。
给你五个整数 m、n、maxMove、startRow 以及 startColumn ，找出并返回可以将球移出边界的路径数量。因为答案可能非常大，返回对 109 + 7 取余 后的结果。

示例 1：
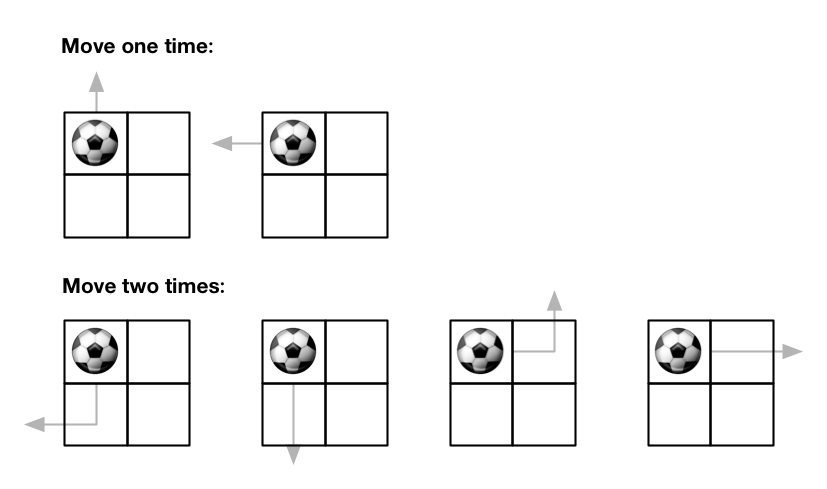
输入：m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0 输出：6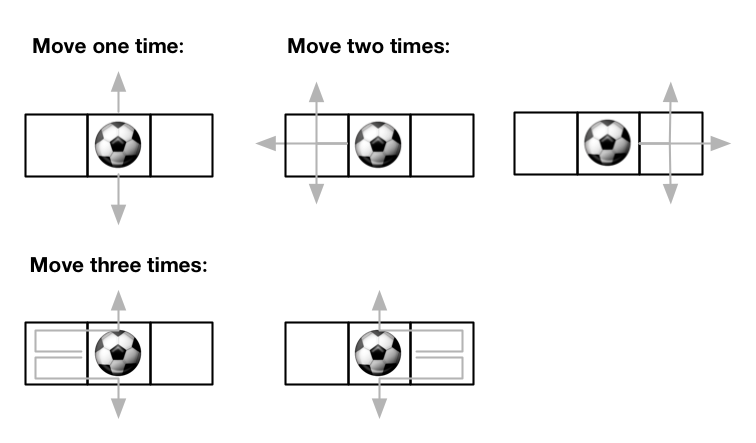
image.png
示例 2：
输入：m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1 输出：12

提示：

  • 1 <= m, n <= 50
  • 0 <= maxMove <= 50
  • 0 <= startRow < m
  • 0 <= startColumn < n

思路：
可以用记忆化搜索，也可以用DP
将整个过程想象成一棵树：
记忆化搜索相当于自上而下
DP相当于自下而上

  1. //记忆化搜索
  2. class Solution {
  3.     final int MOD = (int)(1e9+7);
  4.     int n, m;
  5.     int[][][] f;
  6.     public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
  7.         this.n = m;
  8.         this.m = n;
  9.         f = new int[m][n][maxMove + 1];
  10.         for (int i = 0; i < m; i++)
  11.             for (int j = 0; j < n; j++)
  12.                 Arrays.fill(f[i][j], -1);
  13.         return dp(startRow, startColumn, maxMove);
  14.     }
  15.     int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};
  16.     int dp(int x, int y, int cnt) {
  17.         if (cnt <= 0) {
  18.             return x < 0 || x >= n || y < 0 || y >= m ? 1 : 0;
  19.         }
  20.         if (x < 0 || x >= n || y < 0 || y >= m)
  21.             return 1;
  22.         if (f[x][y][cnt] != -1)
  23.             return f[x][y][cnt];
  25.         long sum = 0;
  26.         for (int i = 0; i < 4; i++) {
  27.             int a = x + dx[i], b = y + dy[i];
  28.             sum = sum + dp(a, b, cnt - 1);
  29.         }
  30.         return f[x][y][cnt] = (int)(sum % MOD);
  31.     }
  32. }
  1. //DP
  2. class Solution {
  3.     static int MOD = 1000000007;
  4.     public int findPaths(int m, int n, int maxMove, int startx, int starty) {
  5.         int[][] f = new int[maxMove + 1][n * m];
  7.         int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};
  8.         for (int i = 1; i <= maxMove; i++) {
  9.             for (int j = 0; j < m * n; j++) {
  10.                 int x = j / n, y = j % n;
  12.                 long res = 0;
  13.                 for (int k = 0; k < 4; k++) {
  14.                     int a = x + dx[k], b = y + dy[k];
  15.                     if (a < 0 || a >= m || b < 0 || b >= n) {
  16.                         res += 1;
  17.                     } else {
  18.                         res += f[i - 1][a * n + b];
  19.                     }
  20.                 }
  21.                 f[i][j] = (int)(res % MOD);
  23.             }
  24.         }
  25.         return f[maxMove][startx * n + starty];
  26.     }
  27. }