
本来没准备打,29的时候突然开了,思路不清就会卡。
6108. 解密消息
给你字符串 key 和 message ,分别表示一个加密密钥和一段加密消息。解密 message 的步骤如下:
- 使用 key 中 26 个英文小写字母第一次出现的顺序作为替换表中的字母 顺序 。
- 将替换表与普通英文字母表对齐,形成对照表。
- 按照对照表 替换 message 中的每个字母。
- 空格 ‘ ‘ 保持不变。
- 例如,key = “hap_py bo_y”(实际的加密密钥会包含字母表中每个字母 至少一次),据此,可以得到部分对照表(’h’ -> ‘a’、’a’ -> ‘b’、’p’ -> ‘c’、’y’ -> ‘d’、’b’ -> ‘e’、’o’ -> ‘f’)。
返回解密后的消息。
示例 1:
输入:key = “the quick brown fox jumps over the lazy dog”, message = “vkbs bs t suepuv” 输出:“this is a secret” 解释:对照表如上图所示。 提取 “the quick brown f_ox jumps over the lazy dog“ 中每个字母的首次出现可以得到替换表。
示例 2:
输入:key = “eljuxhpwnyrdgtqkviszcfmabo”, message = “zwx hnfx lqantp mnoeius ycgk vcnjrdb” 输出:“the five boxing wizards jump quickly” 解释:对照表如上图所示。 提取 “eljuxhpwnyrdgtqkviszcfmabo_” 中每个字母的首次出现可以得到替换表。
提示:
- 26 <= key.length <= 2000
- key 由小写英文字母及 ‘ ‘ 组成
- key 包含英文字母表中每个字符(’a’ 到 ‘z’)至少一次
- 1 <= message.length <= 2000
- message 由小写英文字母和 ‘ ‘ 组成
思路:
找到映射后进行转换
// 赛时代码class Solution {public String decodeMessage(String key, String message) {StringBuilder sb = new StringBuilder();char[] map = new char[26];boolean[] used = new boolean[26];for (int i = 0, j = 0; i < key.length(); i++) {char c = key.charAt(i);if (c >= 'a' && c <= 'z') {if (used[c - 'a']) continue;map[c - 'a'] = (char)(j + 'a');used[c - 'a'] = true;j++;}}for (int i = 0; i < message.length(); i++) {char c = message.charAt(i);if (c >= 'a' && c <= 'z')sb.append(map[message.charAt(i) - 'a']);elsesb.append(c);}return sb.toString();}}
class Solution {public String decodeMessage(String key, String m) {Map<Character, Character> map = new HashMap<>();for (char c : key.replace(" ", "").toCharArray()) {map.putIfAbsent(c, (char)('a' + map.size()));}StringBuilder sb = new StringBuilder();for (int i = 0; i < m.length(); i++)sb.append(map.getOrDefault(m.charAt(i), ' '));return sb.toString();}}
6111. 螺旋矩阵 IV
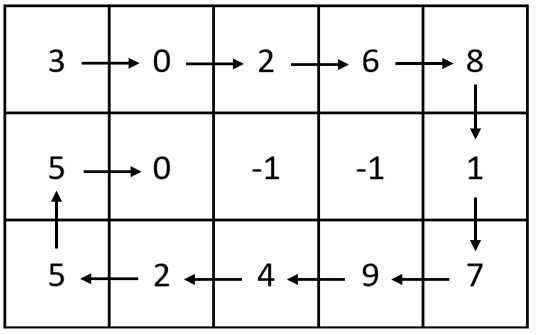

给你两个整数:m 和 n ,表示矩阵的维数。
另给你一个整数链表的头节点 head 。
请你生成一个大小为 m x n 的螺旋矩阵,矩阵包含链表中的所有整数。链表中的整数从矩阵 左上角 开始、顺时针 按 螺旋 顺序填充。如果还存在剩余的空格,则用 -1 填充。
返回生成的矩阵。
示例 1:
输入:m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0] 输出:[[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]] 解释:上图展示了链表中的整数在矩阵中是如何排布的。 注意,矩阵中剩下的空格用 -1 填充。
示例 2:
输入:m = 1, n = 4, head = [0,1,2] 输出:[[0,1,2,-1]] 解释:上图展示了链表中的整数在矩阵中是如何从左到右排布的。 注意,矩阵中剩下的空格用 -1 填充。
提示:
- 1 <= m, n <= 105
- 1 <= m * n <= 105
- 链表中节点数目在范围 [1, m * n] 内
- 0 <= Node.val <= 1000
思路
恶心的模拟
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/class Solution {public int[][] spiralMatrix(int n, int m, ListNode p) {int[][] g = new int[n][m];for (int i = 0; i < n; i++)Arrays.fill(g[i], -1);int[] dx = {0, 1, 0, -1}, dy = {1, 0, -1, 0};for (int x = 0, y = 0, id = 0; p != null; ) {g[x][y] = p.val;p = p.next;int a = x + dx[id], b = y + dy[id];if (a < 0 || a >= n || b < 0 || b >= m || g[a][b] != -1) {id++;id %= 4;a = x + dx[id];b = y + dy[id];}x = a;y = b;}return g;}}
6109. 知道秘密的人数
在第 1 天,有一个人发现了一个秘密。
给你一个整数 delay ,表示每个人会在发现秘密后的 delay 天之后,每天 给一个新的人 分享 秘密。同时给你一个整数 forget ,表示每个人在发现秘密 forget 天之后会 忘记 这个秘密。一个人 不能 在忘记秘密那一天及之后的日子里分享秘密。
给你一个整数 n ,请你返回在第 n 天结束时,知道秘密的人数。由于答案可能会很大,请你将结果对 109 + 7 取余 后返回。
示例 1:
输入:n = 6, delay = 2, forget = 4 输出:5 解释: 第 1 天:假设第一个人叫 A 。(一个人知道秘密) 第 2 天:A 是唯一一个知道秘密的人。(一个人知道秘密) 第 3 天:A 把秘密分享给 B 。(两个人知道秘密) 第 4 天:A 把秘密分享给一个新的人 C 。(三个人知道秘密) 第 5 天:A 忘记了秘密,B 把秘密分享给一个新的人 D 。(三个人知道秘密) 第 6 天:B 把秘密分享给 E,C 把秘密分享给 F 。(五个人知道秘密)
示例 2:
输入:n = 4, delay = 1, forget = 3 输出:6 解释: 第 1 天:第一个知道秘密的人为 A 。(一个人知道秘密) 第 2 天:A 把秘密分享给 B 。(两个人知道秘密) 第 3 天:A 和 B 把秘密分享给 2 个新的人 C 和 D 。(四个人知道秘密) 第 4 天:A 忘记了秘密,B、C、D 分别分享给 3 个新的人。(六个人知道秘密)
提示:
- 2 <= n <= 1000
- 1 <= delay < forget <= n
思路:
这应该是最难的一题了
可以用O(n2)的DP,然后能用前缀和优化为O(n)
class Solution {public int peopleAwareOfSecret(int n, int d, int ft) {// f表示当前有多少人知道秘密// g表示当前有多少人能共享秘密int MOD = (int)(1e9 + 7);int[] f = new int[2 * n + 1];int[] g = new int[2 * n + 1];for (int i = 1; i < 1 + ft; i++) f[i]++;for (int i = d + 1; i < 1 + ft; i++) g[i]++;for (int i = 0; i <= n; i++) {int x = g[i];for (int j = i + d; j < i + ft; j++)g[j] = (g[j] + x) % MOD;for (int j = i; j < i + ft; j++)f[j] = (f[j] + x) % MOD;}return f[n];}}
class Solution {public int peopleAwareOfSecret(int n, int d, int ft) {// f表示当前有多少人知道秘密int MOD = (int)(1e9 + 7);int[] f = new int[2 * n + 1];f[1] = 1;for (int i = 2; i <= n; i++) {int l = Math.max(0, i - ft), r = Math.max(0, i - d);int x = (f[r] - f[l]) % MOD;f[i] = (f[i - 1] + x) % MOD;}int l = Math.max(0, n - ft);return ((f[n] - f[l]) % MOD + MOD) % MOD;}}
6110. 网格图中递增路径的数目
给你一个 m x n 的整数网格图 grid ,你可以从一个格子移动到 4 个方向相邻的任意一个格子。
请你返回在网格图中从 任意 格子出发,达到 任意 格子,且路径中的数字是 严格递增 的路径数目。由于答案可能会很大,请将结果对 109 + 7 取余 后返回。
如果两条路径中访问过的格子不是完全相同的,那么它们视为两条不同的路径。
示例 1: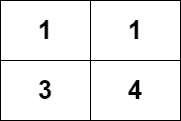
输入:grid = [[1,1],[3,4]] 输出:8 解释:严格递增路径包括: - 长度为 1 的路径:[1],[1],[3],[4] 。 - 长度为 2 的路径:[1 -> 3],[1 -> 4],[3 -> 4] 。 - 长度为 3 的路径:[1 -> 3 -> 4] 。 路径数目为 4 + 3 + 1 = 8 。
示例 2:
输入:grid = [[1],[2]] 输出:3 解释:严格递增路径包括: - 长度为 1 的路径:[1],[2] 。 - 长度为 2 的路径:[1 -> 2] 。 路径数目为 2 + 1 = 3 。
提示:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 1000
- 1 <= m * n <= 105
- 1 <= grid[i][j] <= 105
思路:
记忆化搜索
时间复杂度:O(nm)
空间复杂度:O(nm)
class Solution {int N = 1010, MOD = (int)(1e9 + 7);int[][] f = new int[N][N];int n, m;int[][] g;public int countPaths(int[][] g) {this.g = g;n = g.length;m = g[0].length;for (int i = 0; i < n; i++)Arrays.fill(f[i], -1);int res = 0;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {res = (res + dfs(i, j)) % MOD;}}return res;}int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};int dfs(int x, int y) {if (f[x][y] != -1)return f[x][y];long res = 1;for (int i = 0; i < 4; i++) {int a = x + dx[i], b = y + dy[i];if (a >= 0 && a < n && b >= 0 && b < m && g[a][b] > g[x][y]) {res = (res + dfs(a, b)) % MOD;}}return f[x][y] = (int)(res);}}

