【1】算法学习笔记(1) : 并查集

1. 功能

  1. Union: 合并两个集合
  2. Find: 查询两个元素是否在同一集合

    特别注意每个集合本身的含义是什么！

2. 基本原理

并查集的重要思想在于，用集合中的一个元素代表集合。
每个集合用一棵树来表示，树根的编号就是整个集合的编号，每个节点存储它的父节点。根节点的父节点是它自己。

3. 问题

  1. 初始化

    1. int[] p = new int[N];
    2. void init()
    3. {
    4.  for (int i = 0; i < N; ++i)
    5.      p[i] = i;
    6. }

  2. 如何判断一个节点是不是树根？

p[x] == x 说明该节点是树根

  1. 如何求x所在的集合编号？

    1. int find(int x) {
    2.   if (x == p[x])
    3.      return x;
    4.  return find(p[x]);
    5. }

  2. 如何查询两个元素是否在同一集合？

    1. boolean isConnected(int x, int y) {
    2.   return find(x) == find(y);   
    3. }

  3. 如何合并两个集合？

px是x的集合编号，py是y的集合编号
p[px] = py 或者 p[py] = px 

  1. void merge(int x, int x)
  2. {
  3.     p[find(x)] = find(y);
  4.     //或者
  5.     //p[find(y)] = find(x);
  6. }

  1. 元素脱离集合

    1. void isolate(int x) {
    2.  p[x] = x;   
    3. }

    4. 优化

  2. 路径压缩

采用递归的思想 p[x] = find(p[x]) 

  1. int find(int x) {
  2.      return x == p[x] ? x : (p[x] = find(p[x]))   
  3. }
  1. 按秩合并

根据树的高度，低的向高的上合并。不常用

  1. //使用rank数组记录以每个元素为根节点的子树最大深度(不一定就是树的深度，因为有路径压缩的存在)，初始化每个元素自成一树，rank[i] = 1
  2. int[] p = new int[N];
  3. int[] rank = new int[N];
  4. void init() {
  5.     for (int i = 0; i < N; i++) {
  6.         p[i] = i;
  7.         rank[i] = 1;
  8.     }
  9. }
  11. void merge(int x, int y) {
  12.     //先找到两个根节点
  13.     int px = find(x), py = find(y);
  14.     if (p[px] == p[py])
  15.         return;
  16.     else if (rank[px] <= rank[py]) {
  17.          p[px] = py;
  18.         rank[py] = rank[py] == rank[px] ? rank[py] + 1 : rank[py];
  19.     } else {
  20.          p[py] = px;   
  21.     }
  22. }

例如，合并7和8，右边的树一定优于左边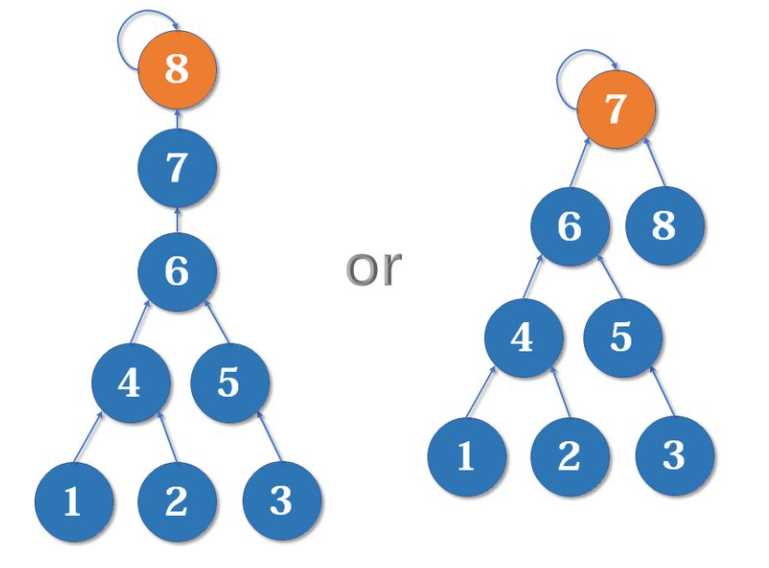
image.png

5. 用类包装好并查集

类封装并查集

6. 带邻域的并查集

1. 集合大小

绑定到根节点

2. 到根节点的距离/偏移量

每个子节点到其父节点的距离

或者 是偏移量：“模意义下的距离”

7. 扩展并查集

一般的并查集每个集合内是一个个元素，而扩展域并查集每个集合内是一个个条件

8. 例题

1. 经典并查集

836. 合并集合
一共有 n 个数，编号是 1∼n，最开始每个数各自在一个集合中。
现在要进行 m 个操作，操作共有两种：

  1. M a b，将编号为 a 和 b 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
  2. Q a b，询问编号为 a 和 b 的两个数是否在同一个集合中；

输入格式
第一行输入整数 n 和 m。
接下来 m 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。
输出格式
对于每个询问指令 Q a b，都要输出一个结果，如果 a 和 b 在同一集合内，则输出 Yes，否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤105
输入样例：

  1. 4 5
  2. M 1 2
  3. M 3 4
  4. Q 1 2
  5. Q 1 3
  6. Q 3 4

输出样例：

  1. Yes
  2. No
  3. Yes
  1. import java.util.*;
  2. import java.io.*;
  4. public class Main {
  5.     public static void main(String[] sss) throws IOException{
  6.         BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
  7.         BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
  9.         String[] str = br.readLine().split(" ");
  10.         int n = Integer.parseInt(str[0]);
  11.         int m = Integer.parseInt(str[1]);
  12.         int[] a = new int[n + 1];
  14.         for (int i = 1; i <= n; i++) a[i] = i;
  16.         while (m -- > 0) {
  17.             str = br.readLine().split(" ");
  18.             int x, y;
  19.             x = Integer.parseInt(str[1]);
  20.             y = Integer.parseInt(str[2]);
  21.             switch (str[0]) {
  22.                 case "M" :
  23.                     a[find(a, x)] = find(a, y);
  24.                     break;
  25.                 case "Q":
  26.                     if (find(a, x) == find(a, y)) {
  27.                         bw.write("Yes\n");
  28.                     } else {
  29.                         bw.write("No\n");
  30.                     }
  31.             }
  33.         }
  35.         br.close();
  36.         bw.close();
  37.     }
  39.     static int find(int[] a, int x) {
  41.         int cur = x;
  42.         while (cur != a[cur]) {
  43.             cur = a[cur];
  44.         }
  46.         while (x != cur) {
  47.             int nx = a[x];
  48.             a[x] = cur;
  49.             x = nx;
  50.         }
  51.         return cur;
  52.     }
  54.     static int find(int[] a, int x) {
  55.          return a[x] == x ? x : (a[x] = find(a[x]));   
  56.     }
  57. }

2. 带邻域的并查集

Acwing 238. 银河英雄传说
并查集 UnionFind - 图2

带权并查集

  1. import java.util.*;
  3. public class Main {
  4.     static final int N = 30010;
  5.     //fa为并查集数组，size只对每个并查集根节点有效，表示该集合元素个数
  6.     //d为距离数组，表示该点到其父节点之间排了多少个元素
  7.     static int[] fa = new int[N], size = new int[N], d = new int[N];
  8.     static {
  9.         for (int i = 0; i < N; i++) {
  10.             fa[i] = i;
  11.             size[i] = 1;
  12.         }
  13.     }
  14.     public static void main(String[] args) {
  15.         Scanner sc = new Scanner(System.in);
  16.         int t = sc.nextInt();
  17.         while (t-- > 0) {
  18.             String op = sc.next();
  19.             int a = sc.nextInt(), b = sc.nextInt();
  20.             int pa = find(a), pb = find(b);
  21.             if (op.equals("M")) {
  22.                 fa[pa] = pb;
  23.                 d[pa] = size[pb];
  24.                 size[pb] += size[pa];
  25.             } else {
  26.                 if (pa != pb)
  27.                     System.out.println(-1);
  28.                 else
  29.                     //有点类似与前缀和的思想，因为在调用query前调用了find，所以query查询的结果一定是该点到根节点的距离
  30.                     System.out.println(Math.max(0, Math.abs(query(a) - query(b)) - 1));
  31.             }
  32.         }
  33.     }
  34.     //find变形
  35.     //在路径压缩压缩的同时由于该点的父节点发生了变化(变成了根节点)，所以要更新该点到其父节点的距离
  36.     static int find(int x) {
  37.         if (fa[x] != x) {
  38.             int root = find(fa[x]);
  39.             d[x] += d[fa[x]];
  40.             fa[x] = root;
  41.         }
  42.         return fa[x];
  43.     }
  44.     static int query(int x) {
  45.         return d[x];
  46.     }
  47. }

3. 扩展并查集

小 A 和小 B 在玩一个游戏。
首先，小 A 写了一个由 0 和 1 组成的序列 S，长度为 N。
然后，小 B 向小 A 提出了 M 个问题。
在每个问题中，小 B 指定两个数 l 和 r，小 A 回答 S[l∼r] 中有奇数个 1 还是偶数个 1。
机智的小 B 发现小 A 有可能在撒谎。

例如，小 A 曾经回答过 S[1∼3] 中有奇数个 1，S[4∼6] 中有偶数个 1，现在又回答 S[1∼6] 中有偶数个 1，显然这是自相矛盾的。

请你帮助小 B 检查这 M 个答案，并指出在至少多少个回答之后可以确定小 A 一定在撒谎。

即求出一个最小的 k，使得 01 序列 S 满足第 1∼k 个回答，但不满足第 1∼k+1 个回答。

输入格式
第一行包含一个整数 N，表示 01 序列长度。
第二行包含一个整数 M，表示问题数量。
接下来 M 行，每行包含一组问答：两个整数 l 和 r，以及回答 even 或 odd，用以描述 S[l∼r] 中有偶数个 1 还是奇数个 1。

输出格式
输出一个整数 k，表示 01 序列满足第 1∼k 个回答，但不满足第 1∼k+1 个回答，如果 01 序列满足所有回答，则输出问题总数量。

数据范围
N≤109,M≤10000
输入样例：
10
5
1 2 even
3 4 odd
5 6 even
1 6 even
7 10 odd
输出样例：
3

方法1：带邻域的并查集
每个集合的含义是集合中的元素两两之间有关系，至于是什么关系，体现在每个元素的邻域中，即其到集合根节点的距离/偏移量。

  1. import java.util.*;
  3. public class Main {
  4.     static final int N = 20010;
  5.     static int idx = 0;
  6.     static int[] fa = new int[N], d = new int[N];
  7.     static Map<Integer, Integer> map = new HashMap<>();
  8.     static {
  9.         for (int i = 0; i < N; i++)
  10.             fa[i] = i;
  11.     }
  13.     static int get(int x) {
  14.         if (!map.containsKey(x)) {
  15.             map.put(x, idx);
  16.             return idx++;
  17.         }
  18.         return map.get(x);
  19.     }
  20.     public static void main(String[] args) {
  21.         Scanner sc = new Scanner(System.in);
  23.         int n = sc.nextInt(), m = sc.nextInt();
  24.         int res = m;
  26.         for (int i = 0; i < m; i++) {
  27.             int a = sc.nextInt() - 1, b = sc.nextInt();
  28.             String op = sc.next();
  29.             a = get(a);
  30.             b = get(b);
  32.             int t = 0;
  33.             if (op.equals("odd"))
  34.                 t = 1;
  36.             int pa = find(a), pb = find(b);
  38.             if (pa == pb) {
  39.                 if ((d[a] ^ d[b]) != t) {
  40.                     res = i;
  41.                     break;
  42.                 }
  43.             } else {
  44.                 fa[pa] = pb;
  45.                 d[pa] = d[a] ^ d[b] ^ t;
  46.             }
  47.         }
  49.         System.out.println(res);
  50.     }
  52.     static int find(int x) {
  53.         if (x != fa[x]) {
  54.             int root = find(fa[x]);
  55.             d[x] ^= d[fa[x]];
  56.             fa[x] = root;
  57.         }
  58.         return fa[x];
  59.     }
  60. }

本题离散化无需保序，因为转化为前缀和之后只涉及到两个独立点的关系，即 s[r] 与 s[l - 1]

方法2：扩展域并查集

  1. import java.util.*;
  3. public class Main {
  4.     static final int N = 40010;
  5.     static int idx;
  6.     static int[] fa = new int[N];
  7.     static Map<Integer, Integer> map = new HashMap<>();
  8.     static {
  9.         for (int i = 0; i < N; i++) {
  10.             fa[i] = i;
  11.         }
  12.     }
  13.     static int get(int x) {
  14.         if (!map.containsKey(x)) {
  15.             map.put(x, idx);
  16.             return idx++;
  17.         }
  18.         return map.get(x);
  19.     }
  20.     public static void main(String[] args) {
  21.         Scanner sc = new Scanner(System.in);
  22.         int n = sc.nextInt(), m = sc.nextInt();
  23.         n = N / 2;
  24.         int res = m;
  26.         for (int i = 0; i < m; i++) {
  27.             int a = sc.nextInt() - 1, b = sc.nextInt();
  28.             String op = sc.next();
  29.             a = get(a);
  30.             b = get(b);
  32.             int pa = find(a), pb = find(b), pa2 = find(a + n), pb2 = find(b + n);
  33.             if (op.equals("even")) {
  34.                 if (pa == pb2) {
  35.                     res = i;
  36.                     break;
  37.                 }
  38.                 fa[pa] = pb;
  39.                 fa[pa2] = pb2;
  40.             } else {
  41.                 if (pa == pb) {
  42.                     res = i;
  43.                     break;
  44.                 }
  45.                 fa[pa] = pb2;
  46.                 fa[pa2] = pb;
  47.             }
  48.         }
  49.         System.out.println(res);
  50.     }
  52.     static int find(int x) {
  53.         return x == fa[x] ? x : (fa[x] = find(fa[x]));
  54.     }
  55. }