1.2 难点释疑

一、首先，要回答为什么一定要采用二进制，而不是我们日常生活中熟悉的十进制。

由于一位二进制数只有1和0两个数值,可以用一个开关电路输出的高电平和低电平表示,所以用于表示1位二进制数值的单元电路结构非常简单,而且对电源电压的稳定度要求也比较低。因为只要能够正确区分出1和0两个不同状态,允许高,低电平在一定范围内波动,也就是说有一个允许的“噪声容限”。例如,在采用5V电源电压系列的CMOS电路中,以4.4V表示1,以0.5V表示0。若噪声容限为电源电压的30% ,那么只要由于电源电压的波动,电路参数的变化以及外界的干扰导致输出电压的变化不超过1.5V ,电路都能正常工作。

如果采用十进制,就要求每个单元电路能够给出十个不同电压等级的输出信号,以代表0~9十个数值。不难想象,组成这样一个单元电路是很困难的。至今尚未见有人设计出可以实际使用的十进制单元电路。而且,即使有这样的单元电路,在工作过程中无论对电源电压稳定度的要求,还是对电路参数精度和稳定性的要求都是比较高的。例如,同样也采用5V的电源电压,则需要将输出电压划分为10个等级,用来表示0~9。这时每个电压等级之间相差将不到0.5V。如果由于电源电压波动、电路参数变化以及外界干扰使输出电平的变化接近0.5V ,则输出电压所表示的数值就可能发生错误。
鉴于以上原因，目前在几乎所有的数字电路（包括各种数字计算机）中，都采用二进制而不采用十进制。
虽然在有些数字电路的应用中有时也会提及“十进制”运算，其实只不过是用4 位二进制数当中的十个状态表示十进制数的十个状态而已，本质上仍然是在用二进制数进行运算。

二、为什么二进制算术运算要采用补码运算？

如果两个正数相加，则比较简单，用第四章中所讲的加法器电路就可以完成了。但如果是两个数相减（也就是两个不同符号的数相加）情况就不同了。首先必须比较两个数绝对值的大小，以确定哪一个作为被减数、哪一个作为减数。然后，让绝对值大的一个数减去绝对值小的一个数。这不仅需要用到比较电路和减法运算电路，而且运算过程也较复杂，影响运算速度。
我们在第二章中已经详细说明了，两个二进制数之间的减法运箕可以用它们的补码相加实现。虽然这需要先求取两个数的补码，但产生补码的电路很简单，而且求取补码和两个数相加的操作可以合并为一步完成。
图1-2-1是一个采用补码运算的加法运算电路原理图。这个电路是在加法器的基础上附加了一组异或门也而形成的。它既可以完成加法运算M+N ，又可以完成减法运算M-N 。

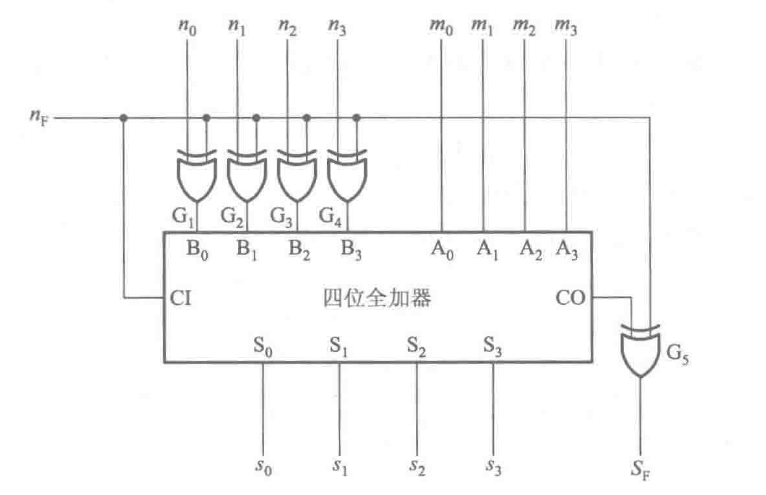
当两个数正数相加时，情况比较简单。因为在正常工作情况下、和数不允许超出1111 ，不会有进位输出，所以CO=0 。同时， N 为正数，它的符号位 。因此，最后的进位输出信号 ，表示S为正数。
当M为正数、N为负数时，，经过反相后，得到的反码，并加到加法器的输入端上。同时，加到加法器的进位输入端，实现“加1”运算。这样就实现了M-N 的运算。在M 的绝对值大千N 的绝对值时，，表示和数为正；在M 的绝对值小于N 的绝对值时，，表示和数为负。
可见，用补码相加进行减法运算不仅运算电路结构简单，而且运算可以一步完成。

1.3 习题类型与解题方法

1.3.1.不同数制间的转换

1）. 将任意进制数转换为等值的十进制数

解题方法和步骤：
利用公式
即可将任何进制的数转换为等值的十进制数。上式中的N为以十进制数表示的计数进位的基数，为第位的系数，它可以是0 ~ N中的任何一个整数。若整数部分有n位，小数部分有m位，则t 将包含从n-1到0的所有正整数和从－1到－m的所有负整数。
对于整数部分为n位、小数部分为m位的二进制数(N=2) ，则得到等值的十进制数为

其中每一位的系数，可能是1或0。

对于整数部分为n位、小数部分为m位的八进制数(N=8) ，则得到等值的十进制数为

其中每一位的系数，可能是0~7当中的某个数值。

对于整数部分为n位、小数部分为m位的十六进制数(N=16) ，则得到等值的十进制数为

式中每一位的系数，的取值可能是0~15当中的某一数值。

2）. 将十进制数转换为等值的二进制数

解题方法和步骤：
若十进制数包含整数和小数，则整数部分和小数部分需按不同方法分别进行转换。
(1) 整数部分的转换 (倒取)
将十进制数除以2，所得余数即二进制数的;
将上面得到的商再除以2，所得余数即二进制数的;
将上面得到的商再除以2，所得余数即二进制数的;
依此类推，直到所得商等于0为止，就得到了等值的二进制数。
(2) 小数部分的转换（顺取）
将十进制数的小数乘以2，所得乘积的整数部分即;
将上面得到的乘积的小数部分再乘以2，所得乘积的整数部分即;
将上面得到的乘积的小数部分再乘以2，所得乘积的整数部分即;
依此类推，直到求出要求的位数为止，就得到了等值的二进制数。

3）. 二进制与八进制和十六进制间的互相转换

解题方法和步骤：
在将二进制数转换为八进制数时，首先将二进制数的整数部分从最低位向高位每3位划分为一组，同时将二进制数的小数部分从最高位向低位每3位划分为一组，然后将每一组代之以等值的八进制数，就得到了所求的转换结果。
在将二进制数转换为十六进制数时，首先将二进制数的整数部分从最低位向高位每4位划分为一组，同时将二进制数的小数部分从最高位向低位每4位划分为一组，然后将每一组代之以等值的十六进制数，就得到了所求的转换结果。
相反地，在将八进制数转换为二进制数时，只需将八进制数的每一位代之以等值的3位二进制数并按原来的顺序排列起来就行了。
同理，在将十六进制数转换为二进制数时，只需将十六进制数的每一位代之以等值的4位二进制数并按原来的顺序排列起来就行了。

4）. 将十进制数转换为等值的八进制和十六进制数

转换方法和步骤：
(1) 首先将十进制数转换为等值的二进制数。
(2) 再将得到的二进制数转换为等值的八进制和十六进制数。

1.3.2.原码、反码、补码之间的转换

在数字电路中是用加在二进制数绝对值前面的符号位表示正、负数的。习惯上用符号位的0表示正数，用符号位的1表示负数。用这种表示方法得到的数码叫做原码。同时还规定，正数的反码和补码与原码相同，所以正数不存在需要转换的问题。

1）. 从负数的原码求反码和补码

解题方法和步骤：
(1) 保持符号位的1不变，将数字部分的每一位求反(1改为0,0改为1) ，就得到了反码。
(2) 在反码的末位上加1，即得到补码。

2）. 从负数的补码求原码

因为＂补码的补码等于原码”，所以将补码再求补，得到的就是原码。

1.3.3.二进制数的补码运算

在数字计算机中，为了简化运算器的电路结构，是用补码相加完成两数相减（不同符号两个数的代数和）运算的。
解题方法和步骤：
(1) 将两个带符号的加数写成补码形式。
(2) 将这两个补码按二进制加法相加，即得补码形式的和。
两数的符号位和来自数值部分的进位相加，所得结果就是和的符号位。这里需要注意两点。
第一，补码相加的和仍为补码，当符号位为1时，和为负数，这时的数值部分不是这个数的绝对值。
第二，将两数写成补码时，数值部分所取的位数必须足以表示和的最大绝对值，否则计算结果将出现错误。