公钥算法和对称钥算法区别

对称加密的优点

速度快，处理量大，适用于对应用数据的直接加密。
加密密钥长度相对较短,如40比特～256比特。
可构造各种加密体制，如产生伪随机数，HASH函数等。

对称加密的缺点

密钥在双方都要一致、保密，传递较难。
大型网络中密钥量大，难以管理，一般需要TTP（KDC）。
密钥需要经常更换
数字签名的问题：传统加密算法无法实现抗抵赖的需求。

公钥加密的优点

只有秘密钥保密，公开钥公开。
密钥生命周期相对较长。
许多公钥方案可以产生数字签名机制。
在大型网络上，所需的密钥相对较少。

公钥加密的缺点

速度慢，处理量少，适用于密钥交换。
密钥长度相对较长。
安全性没有得到理论证明。

公钥算法的思想

公钥密码体制的起源

1976年，Standford Uni. Diffie博士和其导师Hellman 在IEEE Trans. on IT 上发表划时代的文献：
W.Diffie and M.E.Hellman, New Directrions in Cryptography, IEEE Transaction on Information Theory, V.IT-22.No.6, Nov 1976, PP.644-654
这一体制的出现为解决计算机信息网中的安全提供了新的理论和技术基础，被公认为现代够公钥密码学诞生的标志。
1978年，MIT三位数学家R.L.Rivest，A.Shamir和L.Adleman 发明了一种用数论构造双钥体制的方法，称作MIT体制，后来被广泛称之为RSA体制。
信息安全（四）——公私钥密码体制 - 图1

公钥密码体制的基本原理

公钥算法基于数学函数而不是基于替换和置换

使用两个独立的密钥
公钥密码学的提出是为了解决两个问题：
密钥的分配
数字签名

基本思想和要求

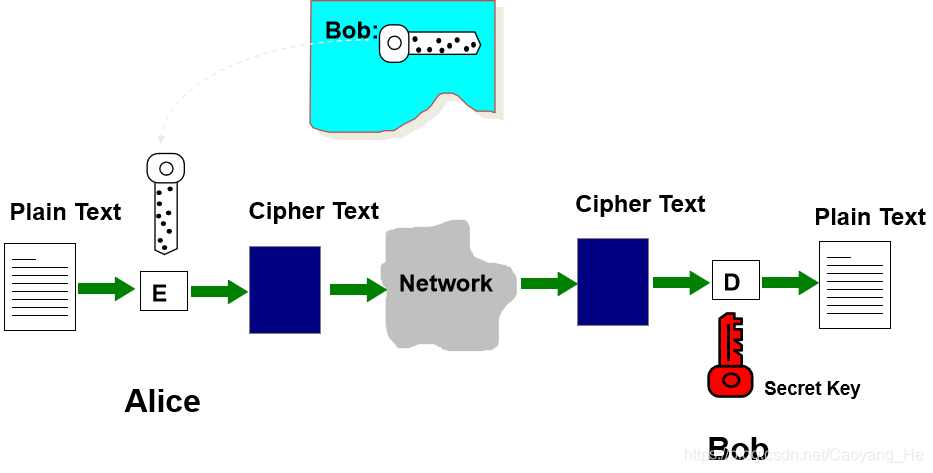
用户拥有自己的密钥对(K,K)，即（公开密钥，私有密钥）
公钥K公开，私钥K保密 A->B：Y=EKUb(X)
B：DK(Y)= DK(EK(X))=X
信息安全（四）——公私钥密码体制 - 图2

公钥体制的主要特点

  • 加密和解密能力分开
  • 多个用户加密的消息只能由一个用户解读，（用于公共网络中实现保密通信）
  • 只能由一个用户加密消息而使多个用户可以解读（可用于认证系统中对消息进行数字签字）。
  • 无需事先分配密钥
  • 密钥持有量大大减少
  • 提供了对称密码技术无法或很难提供的服务：如与哈希函数联合运用可生成数字签名，可证明的安全伪随机数发生器的构造，零知识证明等

基本思想和要求

  • 涉及到各方：发送方、接收方、攻击者
  • 涉及到数据：公钥、私钥、明文、密文

  • 公钥算法的条件：

    • 产生一对密钥是计算可行的
    • 已知公钥和明文，产生密文是计算可行的
    • 接收方利用私钥来解密密文是计算可行的
    • 对于攻击者，利用公钥来推断私钥是计算不可行的
    • 已知公钥和密文，恢复明文是计算不可行的
    • (可选)加密和解密的顺序可交换

如何设计一个公钥算法

  • 公钥和私钥必须相关，而且从公钥到私钥不可推断
    必须要找到一个难题，从一个方向走是容易的，从另一个方向走是困难的
    如何把这个难题跟加解密结合起来
  • 一个实用的公开密钥方案的发展依赖于找到一个陷阱门单向函数。

陷门单向函数

  • 单向陷门函数是满足下列条件的函数f：
    (1)给定x，计算y=fk(x)是容易的；
    (2)给定y，计算x使x=fk-1(y)是不可行的。
    (3)存在k，已知k时,对给定的任何y，若相应的x存在，则计算x使fk-1(y)是容易的。

非对称密钥加密的原理

  • 使用数学上的理论；
  • 数学上某些复杂的计算问题：正向计算容易，反向计算困难。计算机不可能在有效的时间内算出反向结果（从而不可能破解密码）。

  • 例如：

    • 计算两个大数的乘积，非常容易。
    • 分解一个很大的数（如200多位）非常困难，假如这个大数只含有两个非常大的素数（各100多位）作为因子。
    • 背包问题
    • 大整数分解问题（The Integer Factorization Problem, RSA体制）
    • 二次剩余问题
    • 模n的平方根问题
    • 离散对数问题：
    • 有限域的乘法群上的离散对数问题（The Discrete Logarithm Problem, ELGamal体制）
    • 定义在有限域的椭圆曲线上的离散对数问题（The Elliptic Curve Discrete Logarithm Problem，类比的ELGamal体制）

公钥密钥的应用范围

加密/解密
数字签名(身份鉴别)
密钥交换
信息安全（四）——公私钥密码体制 - 图3

Diffie-Hellman密钥协商协议

Diffie-Hellman密钥交换算法

允许两个用户可以安全地交换一个秘密信息，用于后续的通讯过程

算法的安全性依赖于计算离散对数的难度

Diffie-Hellman算法

  1. 双方选择素数p以及p的一个原根a
  2. 用户A选择一个随机数X < p，计算Y=a mod p
  3. 用户B选择一个随机数X < p，计算Y=a mod p
  4. 每一方保密X值，而将Y值交换给对方
  5. 用户A计算出 K=YX mod p
  6. 用户B计算出 K=YX mod p
  7. 双方获得一个共享密钥(amod p)
    注：素数p以及p的原根a可由一方选择后发给对方

Diffie-Hellman算法例：

密钥交换基于素数q = 97和97的一个原根，在这里是a = 5。A和B分别选择秘密密钥X = 36和X = 58。每人计算其公开密钥如下：
Y = 536 = 50 mod 97
Y = 558 = 44 mod 97
在他们交换了公开密钥以后，每人计算共享的秘密密钥如下：
A : K = (Y)X mod 97 = 4436 = 75 mod 97
B : K = (Y)X mod 97 = 5058 = 75 mod 97
从{50，44}出发，攻击者要计算出75很不容易

RSA算法的数学原理

RSA密码体制的建立：

产生密钥对

1、选择两个大素数p,q, p ≠q （p、q 私有，选定）
2、计算n=pq(n<2 ) （n 公开，计算出）
3、选择整数e，使得gcd(e,Φ(n))=1 （e公开，选定的）
4、计算d ≡ e mod Φ(n) (d保密，计算得出的）

公钥: KU={e,n}, 私钥: KR={d,n}

使用

加密: 明文M 解密: M = C mod n

RSA的正确性：

加密：C = Me mod n (M 解密：M = Cd mod n

RSA的实例：

选p = 7，q = 17，则
n = pq = 119，φ(n) = (p-1)(q-1) = 6×16 = 96
取e = 5，它小于96，并且与96互为素数
则d = 77 ( ∵5×77 = 385 = 4×96＋1≡1 mod 96 )
公钥（5，119），私钥（77，119）
加密M = 19
则C = Me mod n = 195 mod 119 = 66 mod 119
解密C = 66
M = Cd mod n = 6677mod 119 = 19 mod 119

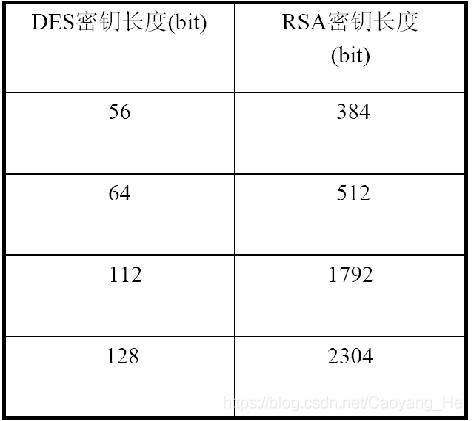
DES和RSA性能比较(同等强度)：

信息安全（四）——公私钥密码体制 - 图4

基础：IFP(Integer Factorization Problem)

加/解密、密钥交换、数字签名

使用最广泛

ElGamal

ElGamal加密算法：

ElGamal加密算法是在密码协议中有着大量应用的一类公钥密码算法，由ElGamal[1984,1985]提出，是除了RSA密码之外最有代表性的公开密钥密码。
是一种基于有限域GF(P)上的离散对数问题的公钥密码体制
既可用于加密，又可用于签名。
选择：一个素数p，p的一个原根(本原元)r，一个整数a(0≦a≦p-2)，令s = r mod P，公开{p, r, s}，保密a。
对于明文信息x，加密：秘密选择随机数k(0≦k≦p-2)，计算(y1，y2)作为密文，其中：y = r mod p， y2 = x s mod p
解密: y(y) mod P
即：( xs ) ( ( r ) )^ -1^ ≡ xr r ^- ak^ ≡ x mod p

ElGamal加密算法是非确定性的，因为每次加密都要选择一个随机数，相同的明文随着加密前随机数k的不同产生不同的密文

基础: DLP(Discrete Logarithm Problem)

加/解密、密钥交换、数字签名

一些数学基础

数论简介：

数论是密码学特别是公钥密码学的基本工具。研究“离散数字集合”的相关问题。

素数和互素数

称整数p(p>1)是素数，如果p的因子只有±1，±p。
若满足下面2个条件，则称c是两个整数a、b的最大公因子，表示为c=gcd(a, b)。
① c是a的因子也是b的因子，即c是a、b的公因子。
② a和b的任一公因子，也是c的因子。
如果gcd(a,b)=1，则称a和b互素。

模运算：

设n是一正整数，a是整数，如果用n除a，得商为q，余数为r，用a mod n表示余数r。
如果(a mod n)=(b mod n)，则称两整数a和b模n同余，记为a≡b mod n。
称与a模n同余的数的全体为a的同余类，记为[a]，称a为这个同余类的表示元素。
注意： 如果a≡0(mod n)，则n|a。

同余有以下性质：
① 若n|(a-b)，则a≡b mod n。
② (a mod n)≡(b mod n)，则a≡b mod n。
③ a≡b mod n,则b≡a mod n。
④ a≡b mod n,b≡c mod n,则a≡c mod n。

求余数运算（简称求余运算）a mod n将整数a映射到集合{0,1, …,n-1}，称求余运算在这个集合上的算术运算为模运算
模运算有以下性质：
[(a mod n)+(b mod n)] mod n = (a+b) mod n
[(a mod n)- (b mod n)] mod n = (a-b) mod n
[(a mod n)×(b mod n)] mod n = (a×b) mod n

费马(Fermat)定理：
p素数，a是整数且不能被p整除，则：ap-1 ≡ 1 mod p
例：a = 7，p = 19，则a = 7 ≡ 1 mod p

欧拉(Euler)函数Φ(n)：
Φ(n)表示小于n且与n互素的正整数个数。例：Φ(6) = 2
p是素数，Φ(p) = p－1 。例：Φ(7) = 6
若n的因子分解为n=∏Piai, ai>0,Pi互不相同,则Φ(n) = ΦPiaiΦ(1－1/Pi)
若gcd(m,n) = 1，则Φ(mn) = Φ(m)Φ(n)，特别地,若pφq，且都是素数，φ(pq)=(p-1)(q-1)。如： φ(21) = 12 = φ(3)× φ(7) = 2×6

Euler定理：
若a与n为互素的正整数,则a ≡ 1 mod n
例：a＝3，n＝10，φ(10)＝4，3＝81 ≡ 1 mod 10
Euler定理的等价形式：
a ≡ a mod n
推论: 若n=pq, p≠q都是素数, k是任意整数,则
mkφ(n) + 1＝mk(p-1)(q-1)+1 ≡ m mod n, 对任意0≤m≤n

原根(Primitive root)
Euler定理表明：对两个互素的整数a，n
a ≡ 1 mod n
定义：存在最小正整数m≤φ(n) (m|φ(n))，使得a ≡ 1 mod n，若对某个a，m=φ(n)，则称a是n的一个原根

离散对数

若a是素数p的一个原根,则对任意整数b，b≠0 mod p，存在唯一的整数i， 1≤i≤(p-1)，使得：b ≡ a mod p，i称为b以(a mod p)的指数(离散对数)，记作ind(b)。
两个性质：
ind(xy) = [ind(x)+ind(y)] mod φ(p)
ind(xr) = [r x ind(x)] mod φ(p)
离散对数的计算：y ≡ g mod p，
已知g，x，p，计算y是容易的
已知y，g，p，计算x是困难的