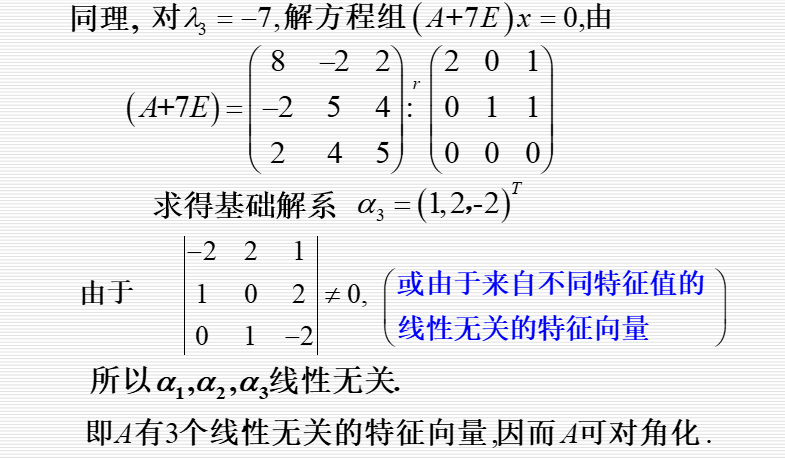
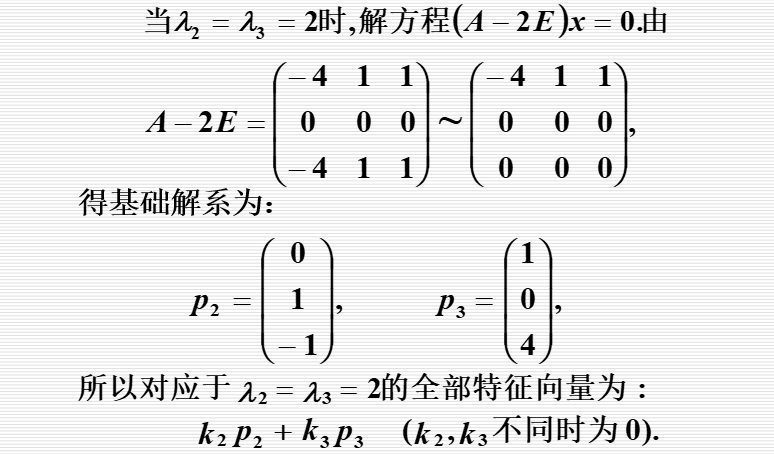
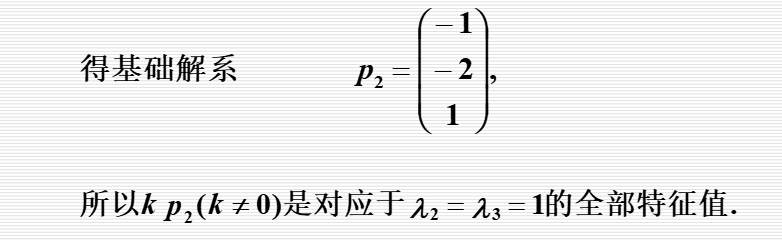方阵的特征值与特征向量

一、特征值与特征向量的概念

定义1
设A是n阶矩阵,如果数λ和n维非零列向量x使关系式 成立,那末,这样的数λ称为方阵A的特征值,非零向_量x称为A的对应于特征值λ的特征向量.

说明
1. 特征向量𝑥≠0,特征值问题是对方阵而言的.
2. 阶方阵的特征值,就是使齐次线性方程组 有非零解的 值 , 即满足方程的λ都是矩阵的特征值；方程组的非零解即为对应于的的特征向量。
3. 
称以λ为未知数的一元n次方程为A的特征方程
记,它是λ的n次多项式,称其为方阵A的特征多项式k+
n阶方阵的特征根在复数域内有n个，其中，重**根的个数按重数计算。**

求方阵的特征值与特征向量的步骤

方阵的特征值与特征向量的性质

性质1 若 是矩阵A的特征值， 是A的对应于的特征向量，则 (1)是的特征值(k≠0是任意常数). (2) 是 的特征值(m是任意常数). (3) 当A可逆时,是 的特征值.

性质2 设n阶方阵 的特征值为,则

性质3 方阵与其转置矩阵的特征值相同. 证明： 故和 的特征值相同.

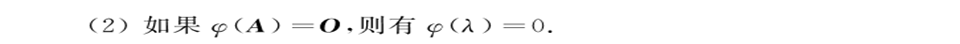
相似矩阵

二、相似矩阵与相似变换的性质
相似变换是一种等价关系，具有：

相似矩阵的性质

相似变换的用处