矩阵的初等变换

定义：下列三种变换称为矩阵的初等行变换
1.对调两行，记作
2.以非零常数 k 乘某一行的所有元素，记作
3.某一行加上另一行的 k 倍，记作

初等变换

• 初等行变换
• 初等列变换

把定义中的“行”换成“列”，就得到矩阵的初等列变换的定义．
矩阵的初等行变换与初等列变换统称为初等变换．

矩阵之间的等价关系

行等价，记作

有限次初等行变换,列变换

列等价，记作

结论：对原线性方程组施行的变换可以转化为对增广矩阵的变换.

**_矩阵之间的等价关系_**<br />**行阶梯形矩阵：**<br />1.**可画出一条阶梯线，线的下方全为零；**<br />2.**每个台阶只有一行；**<br />3.**阶梯线的竖线后面是非零行的第一个非零元素.**<br />**行最简形矩阵：**<br />4.**非零行的第一个非零元为1;**<br />5.**这些非零元所在的列的其它元素都为零.**<br />**标准形矩阵：**<br />6.**左上角是一个单位矩阵，其它元素全为零.**<br />![](https://cdn.nlark.com/yuque/__latex/075bc78862a3cc12d79cafcabdb154e8.svg#card=math&code=%5Cbegin%7Bequation%7D%0A%5Cboldsymbol%7BF%7D%3D%5Cleft%28%5Cbegin%7Barray%7D%7Bcc%7D%0AE_%7Br%7D%20%26%20%5Cboldsymbol%7BO%7D%20%5C%5C%0A%5Cboldsymbol%7BO%7D%20%26%20%5Cboldsymbol%7BO%7D%0A%5Cend%7Barray%7D%5Cright%29_%7Bm%20%5Ctimes%20n%7D%0A%5Cend%7Bequation%7D&id=hDrrw)

结论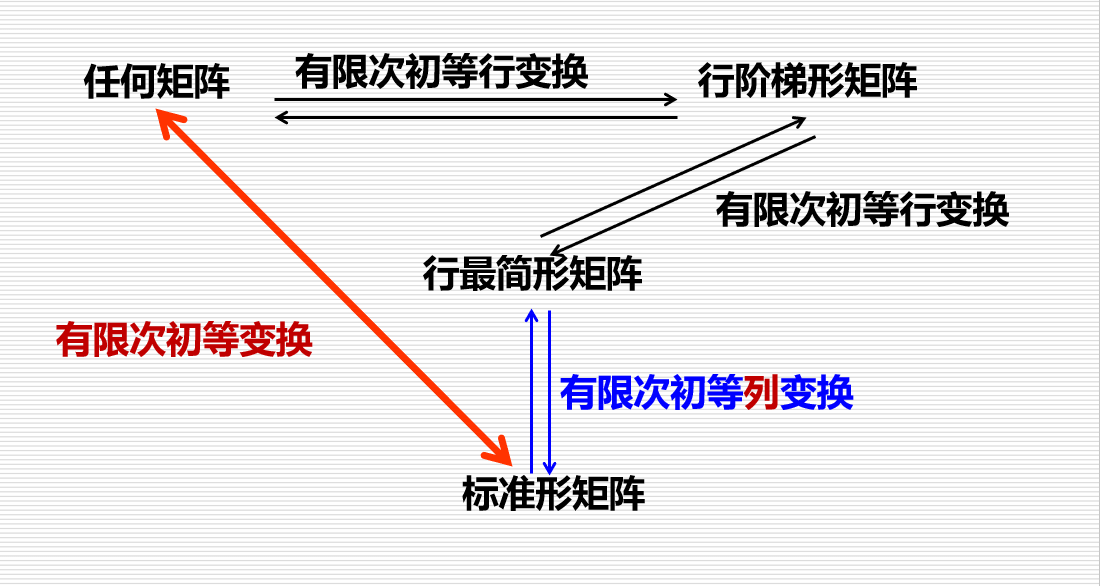

初等变换与矩阵乘法的关系
定义：由单位矩阵 E 经过一次初等变换得到的矩阵称为初等矩阵.

三种初等变换对应着三种初等矩阵.
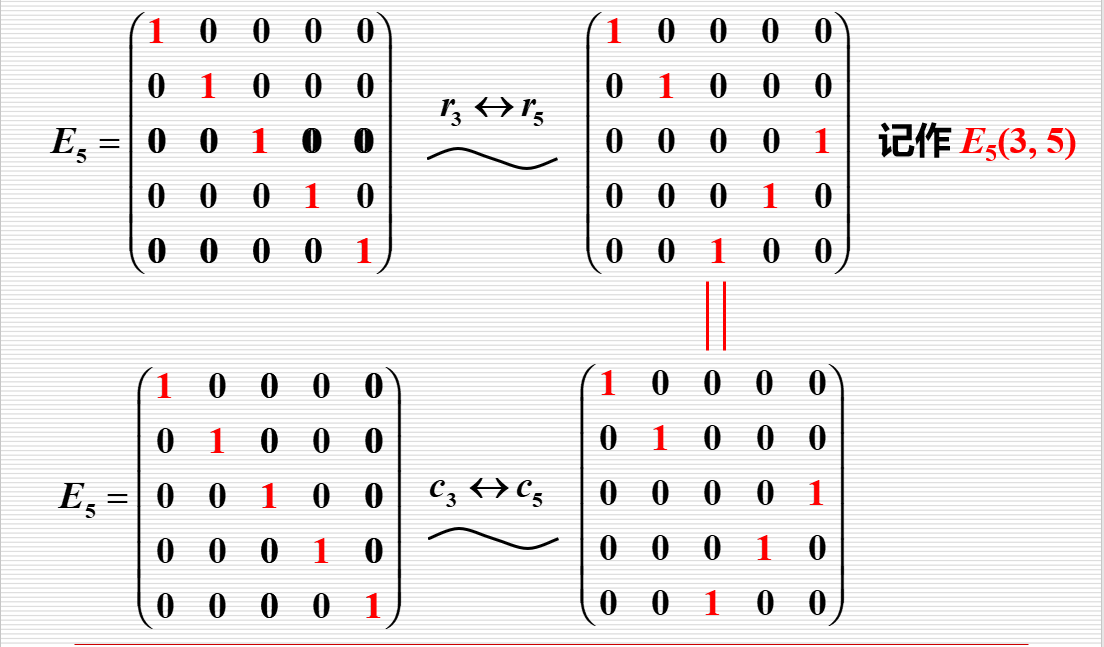
(1)对调单位阵的两行（列）；
(2)以常数k≠0乘单位阵的某一行（列）；
(3)以k乘单位阵单位阵的某一行（列）加到另一行（列）

(1) 对调单位阵的第行（列)， 记作

(2)以常数k≠0乘单位阵第i行（列)，记作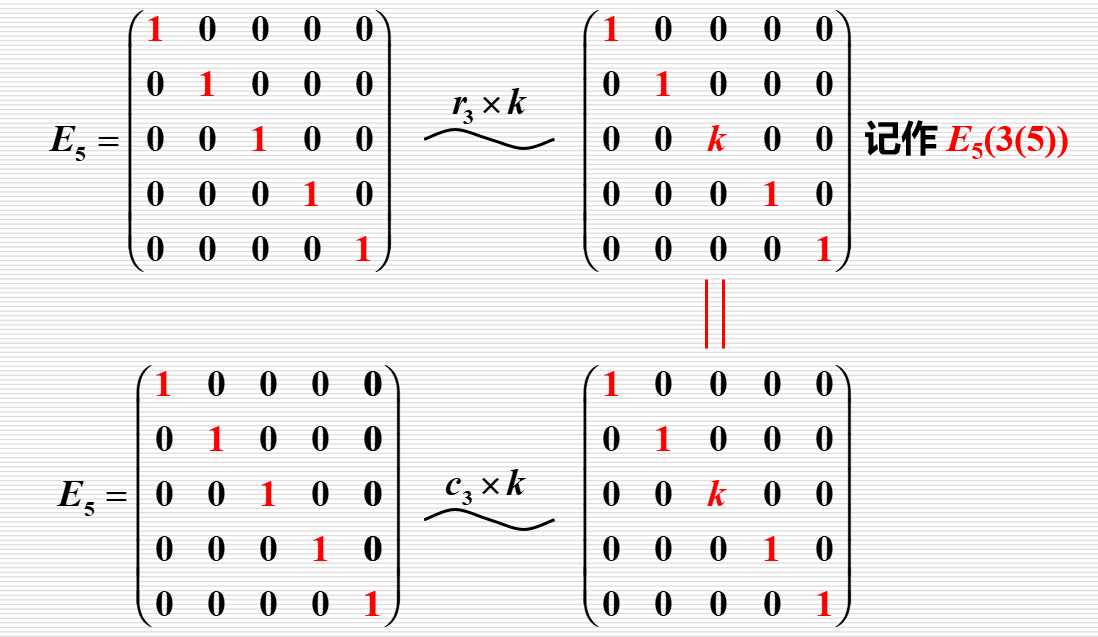

(3)以k乘单位阵第j 行加到第i行,记作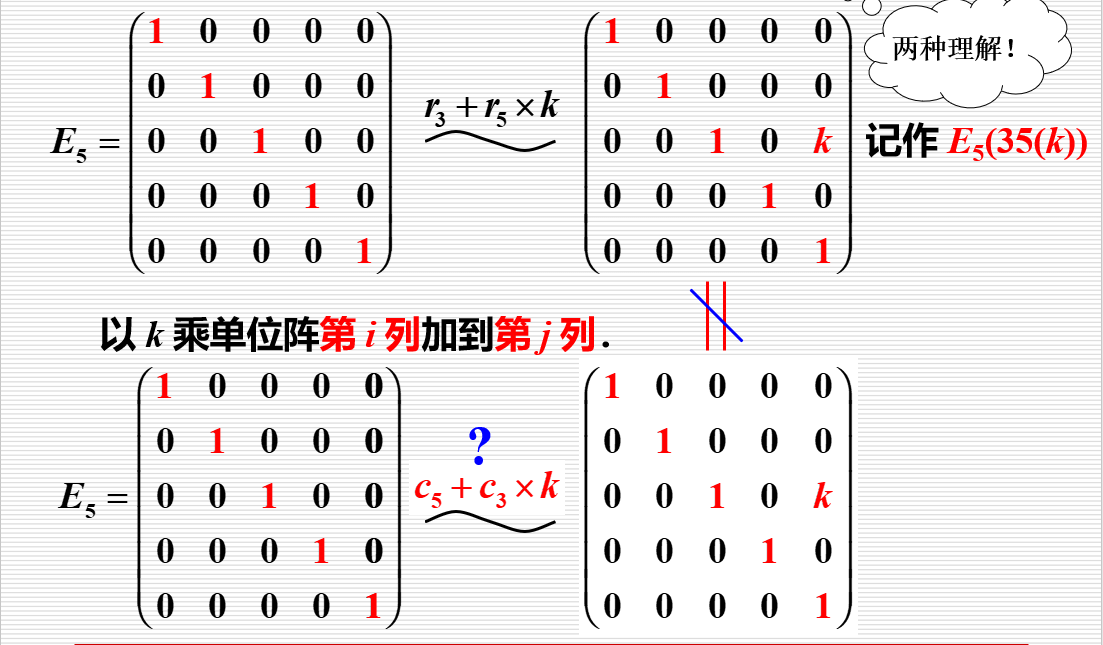

矩阵初等变换的实质

性质1（口诀：左行右列）. 设A是一个 m×n矩阵，

  - **对 _A _施行一次初等行变换，相当于在 _A _的左边乘以相应的 _m _阶初等矩阵；**
  - **对 _A _施行一次初等列变换，相当于在 _A _的右边乘以相应的 _n _阶初等矩阵.**

性质2 方阵A可逆的充要条件是存在有限个初等矩阵，使 ．

这表明，可逆矩阵的标准形矩阵是单位阵. 其实，可逆矩阵的行最简形矩阵也是单位阵．
推论1 方阵A 可逆的充要条件是
推论2 方阵A 与 B 等价的充要条件是存在 m 阶可逆矩阵 P 及 n 阶可逆矩阵 Q ，使 .

初等变换的应用

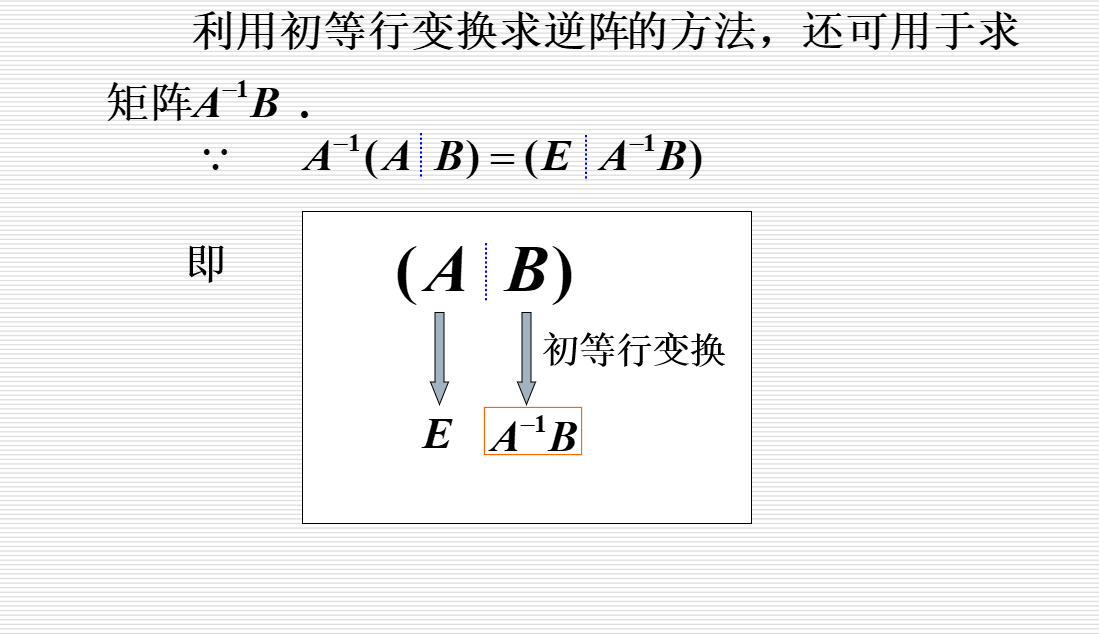
矩阵的秩

矩阵的秩的概念

定义：在 矩阵 A 中，任取 行 列，位于这些行列交叉处的 个元素，不改变它们在 A中所处的位置次序而得的 阶行列式，称为矩阵 A 的 阶式．

显然，m×n矩阵 A 的 k阶子式共有个．

概念辨析：k 阶子式、矩阵的子块、余子式、代数余子式

定义:设矩阵 A 中有一个不等于零的 r 阶子式D，且所有r +1 阶子式（如果存在的话）全等于零，那么D 称为矩阵A的最高阶非零子式，数 r称为矩阵A的秩，记作 ．

规定：零矩阵的秩等于零．

• 根据行列式按行（列）展开法则可知，矩阵 A 中任何一个 r +2 阶子式（如果存在的话）都可以用 r +1 阶子式来表示．
• 如果矩阵 A 中所有 r +1 阶子式都等于零，那么所有 r +2阶子式也都等于零 ．
• 事实上，所有高于 r +1 阶的子式（如果存在的话）也都等于零 ．
• 因此矩阵 A的秩就是 A中非零子式的最高阶数．

矩阵 A的秩就是 A中非零子式的最高阶数．
若矩阵 A中有某个 s阶子式不等于零，则 R(A) ≥ s ；
若矩阵 A中所有 t阶子式等于零，则 R(A) < t．

若A 为 n 阶矩阵，则 A 的 n阶子式只有一个，即|A| ．
当|A|≠0 时， R(A) = n ;
可逆矩阵（非奇异矩阵）又称为满秩矩阵．
当|A| = 0 时， R(A) < n ;
不可逆矩阵（奇异矩阵）又称为降秩矩阵．

若A 为 m×n矩阵，则 0≤R(A)≤min(m, n) ．

矩阵的秩

定理：若 ，则
1.证明 A经过一次初等行变换变为 B，则 R(A)≤R(B) ．
2.B也可经由一次初等行变换变为 A，则 R(B)≤R(A)，于是 R(A) = R(B) ．
3.经过一次初等行变换的矩阵的秩不变，经过有限次初等行变换的矩阵的秩仍然不变．
4.设 A经过初等列变换变为 B，则 经过初等行变换变为 ，从而 ．
又 因此 ．

例题

矩阵的秩的性质
①若A 为 m×n矩阵，则 0≤R(A)≤min(m, n) ．且 R(A)=0的充要条件是A=0
②R(A_T) = _R(A) ．
③若 A ~ B，则 R(A) = R(B)．
④若 P、Q可逆，则 R(PAQ) = R(B)．
⑤max{R(A), R(B)}≤R(A, B)≤R(A)＋R(B)．
特别地，当 B = b为非零列向量时，有R(A)≤R(A, b)≤R(A)＋1．
⑥R(A＋B)≤R(A)＋R(B) ．
⑦R(AB)≤min{R(A), R(B)} ．
⑧若 Am×nBn×l= O，则 R(A)＋R(B)≤n ．

线性方程组的解

线性方程组的表达式
1.一般形式

2.增广矩阵的形式

3.向量方程的形式

4.向量组线性组合的形式

方程组可简化为 ．

线性方程组的解的判定
设有 n个未知数 m个方程的线性方程组

线性方程组的解的判定定理
定理4：n元线性方程组
①无解的充分必要条件是 R(A) < R(A, b)；
②有唯一解的充分必要条件是 R(A) = R(A, b) = n ；
③有无限多解的充分必要条件是 R(A) = R(A, b) < n ．

分析：只需证明条件的充分性，即
R(A) < R(A, b)无解；
R(A) = R(A, b) = n唯一解；
R(A) = R(A, b) < n无穷多解．
那么
无解R(A) < R(A, b) ；
唯一解R(A) = R(A, b) = n；
无穷多解R(A) = R(A, b) < n ．

**_线性方程组的解的定理_**

定理6：n元齐次线性方程组 AX = 0 有非零解的充分必要条件是 R(A) < n ．
定理5：线性方程组 AX = b有解的充分必要条件是R(A) = R(A, b) ．
定理7：矩阵方程 AX = B有解的充分必要条件是R(A) = R(A, B) ．
定理8：设 AB = C，则 R(C) ≤ min{R(A), R(B)} ．

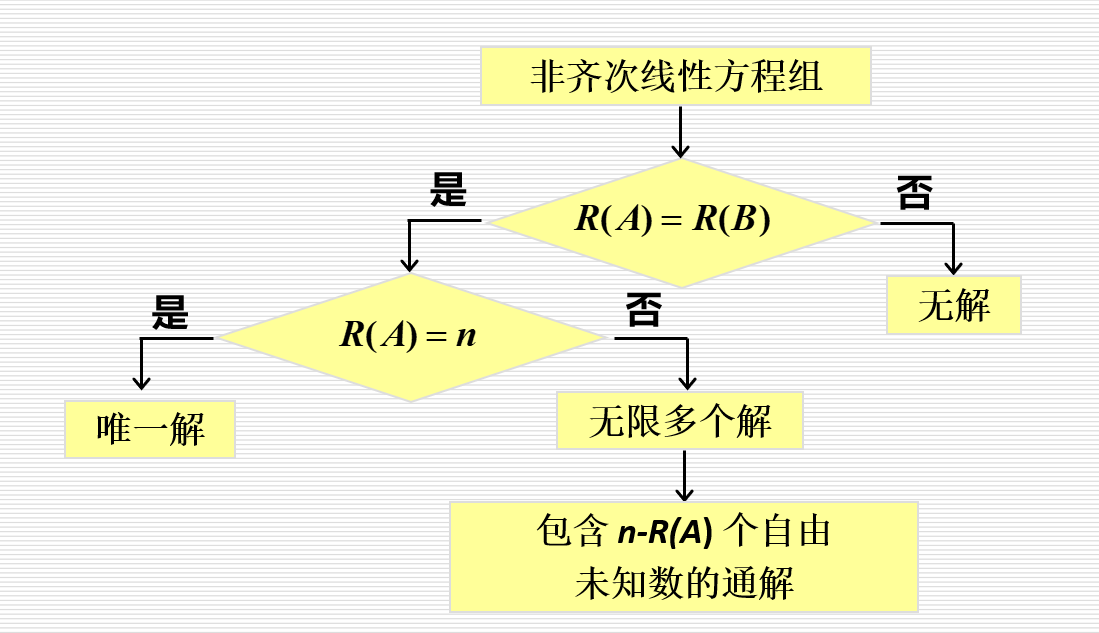
线性方程组的解的定理