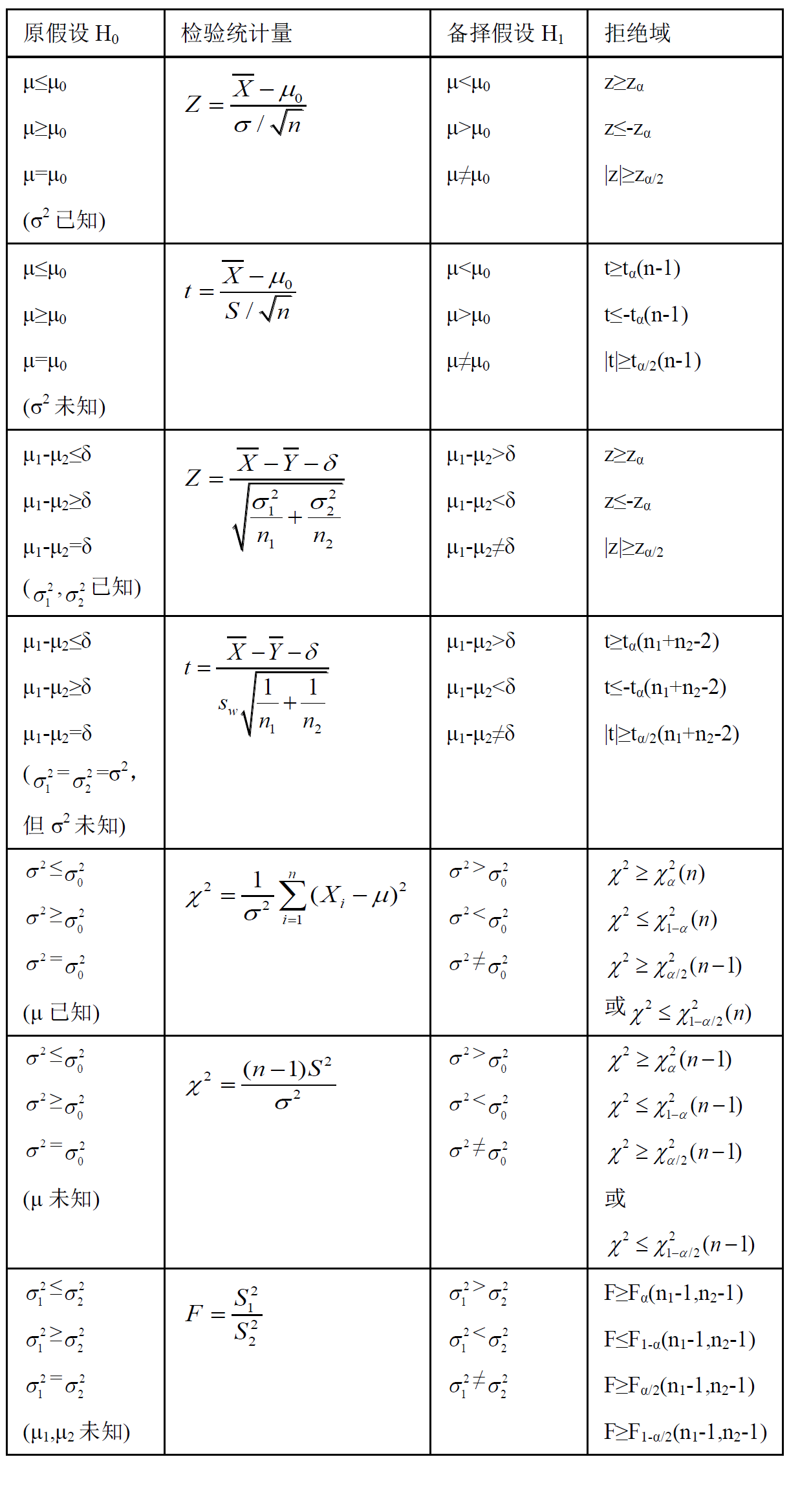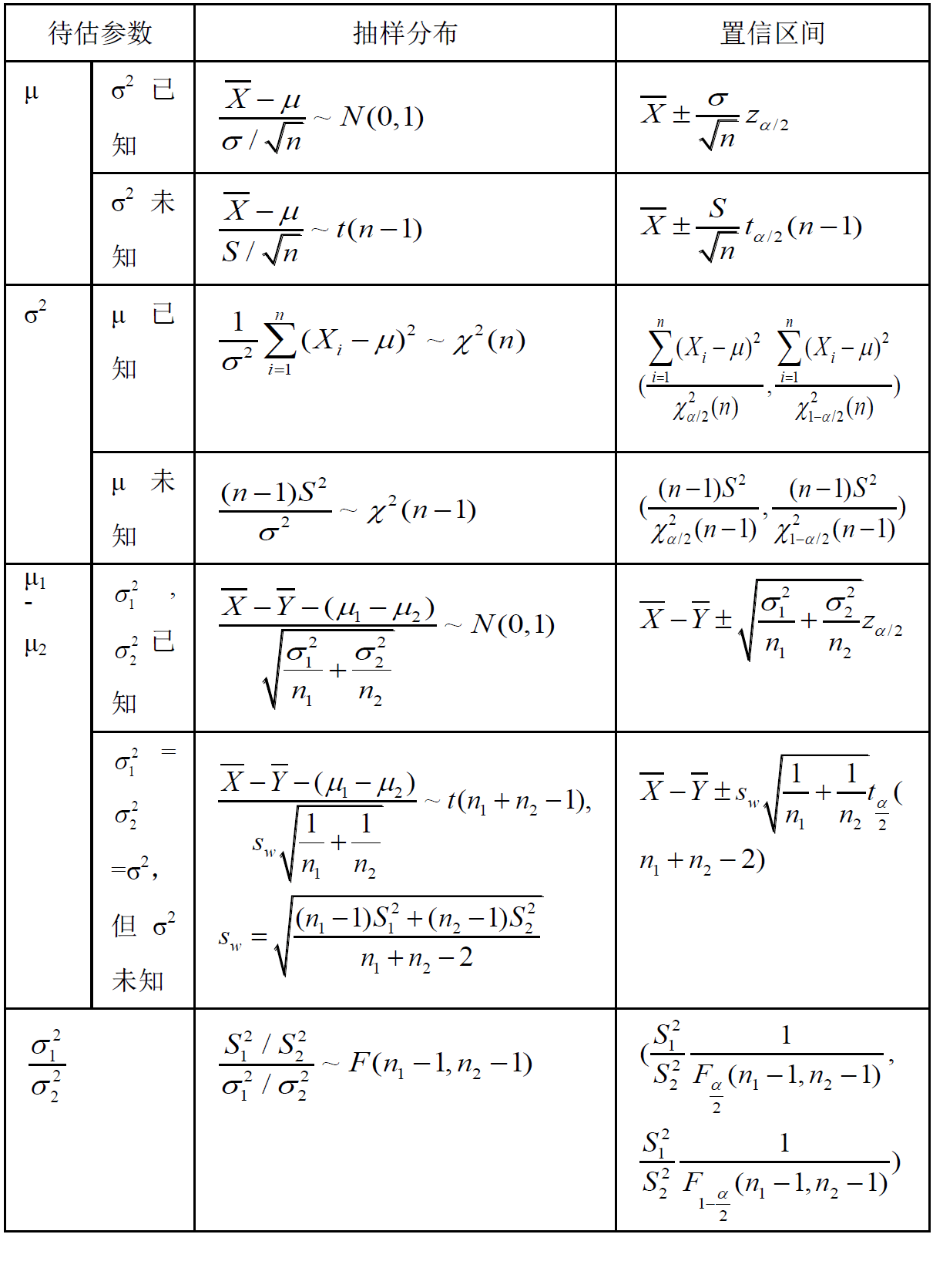1. 第1章 概率论的基本概念

研究和揭示随机现象统计规律性（随机现象有其偶然性的一面，也有其必然性的一面，这种必然性表现为大量观察或试验中随机事件发生的频率的稳定性，即一个随机事件发生的频率经常在某个定值附近摆动，而且，试验次数越多，一般摆动越少，这种规律性我们称之为统计规律性。）的一门学科

1.1 基本概念

随机试验：1.可以重复；2.总体明确；3.单个未知。
样本空间：随机试验E的所有基本结果组成的集合为E的样本空间。
样本点：样本空间的元素称为样本点或基本事件。
随机事件：随机事件是在随机试验中，可能出现也可能不出现，而在大量重复试验中具有某种规律性的事件叫做随机事件(简称事件)。随机事件通常用大写英文字母A、B、C等表示。含有多个样本点的随机事件称为复合事件。
事件发生：
基本事件：仅含一个样本点的随机事件称为基本事件
必然事件：
不可能事件：
差事件：
不相容事件：
对立事件：
逆事件：

1.2 频率和概率

在相同条件下，进行了次试验，在这次试验中，事件A发生的次数称为A发生的频数，比值称为A发生的频率，并记成。
对随机试验的每一事件都赋予一个实数，记为，称为时间的概率。集合函数满足下列条件：
①非负性：；
②规范性：；
③可列可加性：。

当时频率在一定意义下接近于概率。
加法公式%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20transform%3D%22translate(0%2C2945)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-23A7%22%20x%3D%220%22%20y%3D%22-900%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(0%2C-1801.5813263214177)%20scale(1%2C3.0243772550527903)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-23AA%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-23A8%22%20x%3D%220%22%20y%3D%22-2946%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(0%2C-4497.430802448416)%20scale(1%2C3.0243772550527903)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-23AA%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ4-23A9%22%20x%3D%220%22%20y%3D%22-4492%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(1056%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(-11%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(4668%2C2084)%22%3E%0A%3Ctext%20font-family%3D%22monospace%22%20stroke%3D%22none%22%20transform%3D%22scale(71.759)%20matrix(1%200%200%20-1%200%200)%22%3E%E8%8B%A5%3C%2Ftext%3E%0A%3Cg%20transform%3D%22translate(932%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%222137%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(2582%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%223786%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2026%22%20x%3D%224232%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%225571%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(6016%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(7291%2C0)%22%3E%0A%3Ctext%20font-family%3D%22monospace%22%20stroke%3D%22none%22%20transform%3D%22scale(71.759)%20matrix(1%200%200%20-1%200%200)%22%3E%E4%BA%92%3C%2Ftext%3E%0A%3Cg%20transform%3D%22translate(932%2C0)%22%3E%0A%3Ctext%20font-family%3D%22monospace%22%20stroke%3D%22none%22%20transform%3D%22scale(71.759)%20matrix(1%200%200%20-1%200%200)%22%3E%E4%B8%8D%3C%2Ftext%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(1865%2C0)%22%3E%0A%3Ctext%20font-family%3D%22monospace%22%20stroke%3D%22none%22%20transform%3D%22scale(71.759)%20matrix(1%200%200%20-1%200%200)%22%3E%E7%9B%B8%3C%2Ftext%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(2798%2C0)%22%3E%0A%3Ctext%20font-family%3D%22monospace%22%20stroke%3D%22none%22%20transform%3D%22scale(71.759)%20matrix(1%200%200%20-1%200%200)%22%3E%E5%AE%B9%3C%2Ftext%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%223731%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(4259%2C0)%22%3E%0A%3Ctext%20font-family%3D%22monospace%22%20stroke%3D%22none%22%20transform%3D%22scale(71.759)%20matrix(1%200%200%20-1%200%200)%22%3E%E5%88%99%3C%2Ftext%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2212484%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(13402%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-222A%22%20x%3D%221816%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(2705%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-222A%22%20x%3D%224132%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2026%22%20x%3D%225022%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-222A%22%20x%3D%226416%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(7306%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%228581%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%2222651%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2223707%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(24625%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221593%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2226831%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2227832%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(28750%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221593%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2230956%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2026%22%20x%3D%2231956%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2233351%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2234352%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(35270%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221664%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(5956%2C621)%22%3E%0A%3Ctext%20font-family%3D%22monospace%22%20stroke%3D%22none%22%20transform%3D%22scale(71.759)%20matrix(1%200%200%20-1%200%200)%22%3E%E5%B9%BF%3C%2Ftext%3E%0A%3Cg%20transform%3D%22translate(932%2C0)%22%3E%0A%3Ctext%20font-family%3D%22monospace%22%20stroke%3D%22none%22%20transform%3D%22scale(71.759)%20matrix(1%200%200%20-1%200%200)%22%3E%E4%B9%89%3C%2Ftext%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(1865%2C0)%22%3E%0A%3Ctext%20font-family%3D%22monospace%22%20stroke%3D%22none%22%20transform%3D%22scale(71.759)%20matrix(1%200%200%20-1%200%200)%22%3E%E7%9A%84%3C%2Ftext%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%222798%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%223077%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%223828%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%224218%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-222A%22%20x%3D%225190%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%226080%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%226840%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%227507%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%228563%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%229315%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%229704%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2210455%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2211066%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2212067%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2212819%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%2213208%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2213968%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%2214579%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2215580%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2216331%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%2216721%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%2217471%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2218231%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%2218898%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2219955%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2220706%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%2221096%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2221846%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2222458%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2223458%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2224210%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(24599%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%2235%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(139%2C281)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-AF%22%20x%3D%22-70%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(355.5131578947368%2C0)%20scale(0.07894736842105263%2C1)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-AF%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-AF%22%20x%3D%22320%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%2225559%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2226318%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%2226986%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2228042%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2228794%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%2229183%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2229943%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2230554%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2231555%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2232306%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(32696%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%2235%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(83%2C248)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-AF%22%20x%3D%22-70%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(353.7804709141274%2C0)%20scale(0.1038781163434903%2C1)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-AF%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-AF%22%20x%3D%22329%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%2233609%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2234359%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(6084%2C-770)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%22751%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%221141%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-222A%22%20x%3D%222113%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%223003%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-222A%22%20x%3D%223985%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-43%22%20x%3D%224874%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%225635%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%226302%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%227358%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%228110%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%228499%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%229250%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%229862%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2210862%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2211614%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%2212003%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2212763%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2213375%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2214375%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2215127%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-43%22%20x%3D%2215516%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2216277%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%2216889%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2217889%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2218641%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%2219030%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%2219781%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2220540%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%2221152%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2222153%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2222904%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%2223294%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-43%22%20x%3D%2224044%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2224805%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%2225416%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2226417%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2227169%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%2227558%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-43%22%20x%3D%2228318%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2229078%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2229690%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2230691%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2231442%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%2231832%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-42%22%20x%3D%2232582%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-43%22%20x%3D%2233342%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2234102%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(0%2C-2015)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(918%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ1-22C3%22%20x%3D%220%22%20y%3D%22-1%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%221178%22%20y%3D%22675%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(833%2C-286)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%22345%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221124%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(2638%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%223733%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%225318%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(6374%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ1-2211%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%221494%22%20y%3D%22675%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1056%2C-287)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%22345%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221124%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%228846%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(9764%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%221484%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%2211860%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(12861%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ1-2211%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1056%2C-287)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2264%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%221279%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-3C%22%20x%3D%221624%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6A%22%20x%3D%222403%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2264%22%20x%3D%222815%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%223594%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2217150%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(18068%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(1484%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6A%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%222626%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2221307%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(22307%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ1-2211%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1056%2C-287)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2264%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%221279%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-3C%22%20x%3D%221624%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6A%22%20x%3D%222403%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-3C%22%20x%3D%222815%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6B%22%20x%3D%223594%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2264%22%20x%3D%224115%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%224894%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2227516%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(28434%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(1484%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6A%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(2626%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6B%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%223845%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2232891%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2026%22%20x%3D%2233892%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%2235287%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2236288%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%2236677%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%2237456%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(37956%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C362)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%22600%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221379%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%2239775%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(40693%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(389%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(1593%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2026%22%20x%3D%222964%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(4304%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-41%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%221061%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%225579%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bc%7D%0A%5Ctext%20%7B%20%E8%8B%A5%20%7D%20A%7B1%7D%2C%20A%7B2%7D%2C%20%5Cldots%2C%20A%7Bn%7D%20%5Ctext%20%7B%20%E4%BA%92%E4%B8%8D%E7%9B%B8%E5%AE%B9%2C%20%E5%88%99%20%7D%20P%5Cleft%28A%7B1%7D%20%5Ccup%20A%7B2%7D%20%5Ccup%20%5Cldots%20%5Ccup%20A%7Bn%7D%5Cright%29%3DP%5Cleft%28A%7B1%7D%5Cright%29%2BP%5Cleft%28A%7B2%7D%5Cright%29%2B%5Cldots%2BP%5Cleft%28A%7Bn%7D%5Cright%29%20%5C%5C%0A%5Ctext%20%7B%20%E5%B9%BF%E4%B9%89%E7%9A%84%2C%20%7D%20P%28A%20%5Ccup%20B%29%3DP%28A%29%2BP%28B%29-P%28A%20B%29%3DP%28A%29%2BP%28%5Cbar%7BA%7D%20B%29%3DP%28B%29%2BP%28%5Cbar%7BB%7D%20A%29%20%5C%5C%0AP%28A%20%5Ccup%20B%20%5Ccup%20C%29%3DP%28A%29%2BP%28B%29%2BP%28C%29-P%28A%20B%29-P%28A%20C%29-P%28B%20C%29%2BP%28A%20B%20C%29%20%5C%5C%0AP%5Cleft%28%5Cbigcup%7Bi%3D1%7D%5E%7Bn%7D%20A%7Bi%7D%5Cright%29%3D%5Csum%7Bi%3D1%7D%5E%7Bn%7D%20P%5Cleft%28A%7Bi%7D%5Cright%29-%5Csum%7B1%20%5Cleq%20i%3Cj%20%5Cleq%20n%7D%20P%5Cleft%28A%7Bi%7D%20A%7Bj%7D%5Cright%29%2B%5Csum%7B1%20%5Cleq%20i%3Cj%3Ck%20%5Cleq%20n%7D%20P%5Cleft%28A%7Bi%7D%20A%7Bj%7D%20A%7Bk%7D%5Cright%29%2B%5Cldots%2B%28-1%29%5E%7Bn%2B1%7D%20P%5Cleft%28A%7B1%7D%20A%7B2%7D%20%5Cldots%20A_%7Bn%7D%5Cright%29%0A%5Cend%7Barray%7D%5Cright.&id=IwrP6)

减法公式

1.3 等可能概型（古典概型）

１. 样本空间包含有限个元素。
２. 每个基本事件发生的可能性相同。
具有以上两个特点的试验称为等可能概型，也叫古典概型。

1.4 条件概率

设 是两个事件，且，称为在事件A 发生的条件下事件B 发生的条件概率。
乘法公式
全概率公式
贝叶斯公式

1.5 独立性

设是两个事件，如果满足等式，则称事件相互独立，简称独立。
与相互独立

2. 第2章 随机变量及其分布

2.1 随机变量

设随机试验的样本空间为是定义在样本空间上的实值单值函数，称为随机变量。
随机变量的取值随随机试验的结果而定，在试验之前不能预知它取什么值，且它的取值有一定的概率。这些性质显示了随机变量与普通函数有着本质的差异。

2.2 离散型随机变量及其分布律

如果随机变量全部可能的取值是有限个或可列无限个，则称为离散型随机变量。

几个常见分布：

• [x] １. 0-1 分布

• [x] ２. 二项分布

• [x] ３. 泊松分布

４. 几何分布

• ５. 超几何分布

  2.3 随机变量的分布函数

  设是一个随机变量，是任意实数，函数称为的分布函数。分布函数具有以下性质：
  １. 是一个不减函数
  ２.
  ３.即是右连续的

  2.4 连续型随机变量及其概率密度

  如果对于随机变量的分布函数，存在非负函数，使得对于任意实数，均有则称为连续型随机变量，其中函数称为的概率密度函数，简称概率密度。

概率密度具有以下性质：
１.
２.
３.
４.若在点处连续，则有

几个常见分布：

• [x] １. 均匀分布

• [x] ２. 指数分布指数分布和几何分布具有“无记忆性”

• [x] ３. 正态分布记为特别地，当时，称服从标准正态分布。正态分布具有以下性质

• (1)

(2)
(3)
(4)

2.5 随机变量函数的分布

求随机变量函数的分布：
１. 离散型随机变量函数的分布
列举法：逐点求出Y 的值，概率不变，相同值合并
２. 连续型随机变量函数的分布
(1) 分布函数法
(2) 公式法
如果处处可导且恒有，则也是连续型随机变量，其概率密度为其中是的反函数。

3. 第3章 多维随机变量及其分布

3.1 二维随机变量

设随机试验的样本空间为和是定义在样本空间上的两个随机变量，由它们构成的一个向量，叫做二维随机向量或二维随机变量。
设是一个二维随机变量，是任意实数，函数称为二维随机变量的分布函数，或称为随机变量和的联合分布函数。
分布函数具有以下性质：
１. 是变量和的不减函数。
２. ，且。
３. 关于右连续，关于也右连续。
４.对于任意的 ， 有。

如果二维随机变量全部可能取到的值是有限个或可列无限个，则称为离散型二维随机变量。是的分布律
如果对于二维随机变量的分布函数，存在非负函数，使得对于任意实数，均有则称为连续型二维随机变量，其中函数称为的概率密度，或称为随机变量和的联合概率密度。

概率密度具有以下性质：
１.
２.
３.
４.若在点处连续，则有

3.2 边缘分布

• 边缘分布函数：
• 边缘分布律：

• [x] 边缘概率密度：

  3.3 条件分布

  条件分布率
  条件概率密度

  3.4 相互独立的随机变量

  和相互独立(连续型)(离散型)

  3.5 二维随机变量函数的分布

  １. 离散型二维随机变量，列举法
  ２. 连续型二维随机变量
  (1) 分布函数法
  (2) 公式法

• [x] ①

• X，Y对称

当和相互独立时，有卷积公式

②

4. 第4章 随机变量的数字特征

4.1 数学期望

离散型
连续型

性质：

• 1.
• 2.
• 3.

• [x] 4.

  4.2 方差

• [x]

性质：

• 1
• 2
• 3
• 4

常见分布的数字特征：
离散型：

• [x] 1.0-1 分布

• [x] 2.二项分布

• [x] 3.泊松分布

4.几何分布

5.超几何分布

连续型：

• [x] 1.均匀分布

• [x] 2.指数分布

• [x] 3.正态分布

4.3 协方差及相关系数

协方差
性质：
1
2

• 相关系数

性质：
1
2

独立一定不相关，不相关不一定独立。
对于二维正态分布，独立与不相关等价。

4.4 矩、协方差矩阵

5. 第5章 大数定律和中心极限定理

5.1 大数定律

１. 切比雪夫(Chebyshev)大数定律

设随机变量相互独立，期望和方差都存在，且它们的方差有公共上界，则对于任意实数，有

• 切比雪夫不等式

  ２. 伯努力大数定律

  设随机变量相互独立且都服从参数为的分布，则对于任意实数，有

３. 辛钦大数定律

设随机变量相互独立,服从统一分布，且具有共同的数学期望，则对于任意实数，有

5.2 中心极限定理

１. 列维-林德伯格定理（独立同分布的中心极限定理）设随机变量相互独立，服从同一分布，且具有共同的期望和方差，则

• ，即

２. 李雅普诺夫(Liapunov)定理设随机变量相互独立，他们具有数学期望和方差：

记，若存在正数，使得当时，，则

３. 棣莫弗-拉普拉斯(De Moivre-Laplace)定理（二项分布以正态分布为极限）

6. 第6章 数理统计的基本概念

6.1 随机样本

随机试验全部可能的观察值称为总体。
每一个可能观察值称为个体。
一个总体对应于一个随机变量，一般不区分总体与相应随机变量，笼统称为总体。
被抽取的部分个体叫做总体的一个样本。
来自总体的个相互独立且与总体同分布的随机变量称为简单随机变量。

6.2 抽样分布

设是来自总体的一个样本，是一个连续函数，若中不含未知参数，则称是一个统计量。
常用的统计量：
样本均值
样本方差
样本阶原点矩
样本阶中心矩
经验分布函数，表示值小于的随机变量的个数。

来自正态总体的几个常用抽样分布：
１.分布
设是来自总体的样本，则称统计量服从自由度为的分布，记为
现，由定义，即，再由分布的可加性知，。

２. 分布
设，且相互独立，则称随机变量服从自由度为的分布，记为。
当足够大时，分布近似于分布。分布的上分位点记为，由其概率密度的对称性知

３. 分布
设，且相互独立，则称随机变量服从自由度为的分布，记为。
分布的性质：
(1).若,则。
(2).若，则。
分布的上α 分位点记为，，

正态总体样本均值与样本方差的抽样分布：

• 首选，不论服从什么分布，总有
• １.
• ２.，且与相互独立
• ３.

４.，若，则，

第7章 参数估计

7.1 点估计

设总体的分布函数的形式为已知，但它的一个或多个参数未知，借助于总体的一个样本来估计未知参数的值称为参数的点估计。

１. 矩估计法
用样本原点矩来估计总体的原点矩，用样本的中心矩来估计总体的中心矩。

２. 最大似然估计法
(1) 写出似然函数
(2) 求出使达到最大值的.
是个乘积的形式，而且与在同一处取极值，因此的最大似然估计量（对数似然方程）求得。
(3) 用作为的估计量。

7.2 估计量的评价标准

１. 无偏性
２. 有效性
３. 相合性

7.3 区间估计

设总体的分布函数含有一个未知参数，对于给定值，若由来自的样本确定的两个统计量
和，，对于任意满足，则称随机区间是的置信水平为的置信区间。
置信水平为的置信区间不是唯一的。区间越小表示估计的精度越高。

7.4 正态总体期望与方差的区间估计

第8章 假设检验

拒绝域：当检验统计量落入其中时，则否定原假设。

小概率事件原理：小概率事件在一次试验中实际上不会发生，若在一次试验中发生了，就认为不合理，小概率的值常根据实际问题的要求，规定一个可以接受的充分小的数，当一个事件的概率不大于时，就认为它是小概率事件。称为显著性水平。

统计推断有两类错误，弃真和存伪，只对犯第一类错误的概率加以控制，而不考虑第二类错误的检验称为显著性检验。就是允许犯第一类错误的概率的最大允许值。

假设检验的基本步骤；
１. 根据实际问题的要求，提出原假设和备择假设；
２. 给定显著性水平和样本容量；
３. 确定检验统计量以及拒绝域的形式；
４. 按求出拒绝域；
５. 取样，根据样本观察值做出决策，是接受还是拒绝。

8.2 正态总体样本均值与样本方差的假设检验