集合论也称集论，是研究集合（由一堆抽象物件构成的整体）的数学理论，包含了集合、元素和成员关系等最基本的数学概念。
集合论是数学史上最富创造性的伟大成果之一，是现代数学的一个重要分支，在数学中占有一个独特的地位，其基本概念已渗透到数学的所有领域。
集合论由德国数学家康托尔于19世纪末创立。十七世纪，数学中出现了一门新的分支：微积分。在之后的一二百年中这一崭新学科获得了飞速发展并结出了丰硕的成果，其推进速度之快使人来不及检查和巩固它的理论基础。十九世纪初，许多迫切问题得到解决后，出现了一场重建数学基础的运动。在这场运动中，康托尔开始探讨了前人从未碰过的实数点集，这便是集合论研究的开端。1873年12月7日，康托尔在给戴德金的信中最早提出了集合论的思想，这一天也被称为集合论的诞生日。1874年康托尔正式提出了“集合”的概念，他对集合所下的定义是：把若干确定的有区别的事物（不论是具体的或抽象的）合并起来，看作一个整体，就称为一个集合，其中各事物称为该集合的元素。
在大多数现代数学的公式化中，集合论提供了要如何描述数学物件的语言。集合论和逻辑与集合论和逻辑与一阶逻辑共同构成了数学的公理化基础，以未定义的“集合”与“集合成员”等术语来形式化地建构数学物件。按现代数学观点，数学各分支的研究对象或者本身是带有某种特定结构的集合如群、环、拓扑空间，或者是可以通过集合来定义的（如自然数、实数、函数）。从这个意义上说，集合论可以说是整个现代数学的基础。
本篇主要介绍集合的基本知识及关系与函数这两种特殊集合的基本概念和基本特征。

第3章 集合

• 集合简称集，是数学中的一个基本概念，也是集合论的主要研究对象。集合的概念由德国数学家康托尔首先提出：把若干确定的有区别的事物合并起来，看作一个整体，就称为一个集合，其中各事物称为该集合的元素。

• 本章主要介绍集合的基本知识，包括集合的概念与表示方法、集合之间的关系与集合的运算、序偶与笛卡尔积、集合的包含排斥原理及集合的划分与覆盖，最后通过一个实例介绍了运用集合的基本知识提高通信过程中纠错效率的方法。

  3.1 集合的概念和表示法

  3.1.1 集合的概念

• （1）集合的概念

  • 集合是具有某种特定性质的对象汇集成的一个整体。作为数学上的基本概念，如同几何中的点、线、面等概念一样，集合是一个很难用其他概念精确定义的原始概念。那么，集合的定义是什么呢？集合论的创始人德国数学家康托尔于1874年最先给出了集合的经典定义：
  • 定义3.1 集合 由人们直观上或思想上能够明确区分的一些对象所构成的一个整体叫做集合。其中，集合是总体，而集合中含有的对象或客体称为集合中的元素或成员，是组成总体的个体。

    1. 集合中元素所表示的事物可以是具体的，也可以是抽象的。如学生、课桌、电路等具体事物，及概念、观念、数据类型等抽象描述。
    2. 集合的元素可以是任意的。例如：一个学生、一张课桌、一个字母、一双鞋子、离散数学等元素可以组成一个集合。尽管这样的集合可能没人关心，但将这些元素集中在一起，也符合集合的概念，也是可以接受的。
    3. 集合中的元素具有互异性。如“计算机学院的全体学生”这个集合中，计算机学院的每个学生，都只能是该集合中的一个元素，不容许在集合中重复出现。
    4. 集合的元素必须是确定和可区分的。例如“计算机学院的中年教师”这种客体就不易表示一个集合，这是因为“中年”是一个界定不清的概念，什么年龄段的教师才能算中年？没有一个明确的划分或界定，不同情况有不同的界定方法。那么，这样的元素就不能构成集合。

    • 一般情况下，集合的名称用大写英文字母A、B、C、……等表示，而小写英文字母a、b、c、……等常用来表示集合的元素。
    • 元素和集合之间是隶属关系，即“属于”或“不属于”的关系。若元素a属于集合A，则用a∈A表示，亦称a是A的元素；若元素a不属于集合A，则用a∉A表示，亦称a不是A的元素。
    • 由于元素和集合之间是“属于”或“不属于”的关系，因此，集合与命题之间有很紧密的联系。元素“属于”或“不属于”某集合可以看做是一个命题，若元素a确实属于集合A，则命题“a∈A”的真值为“真”，相应的，命题“a∉A”的真值为“假”；若元素a不属于集合A，则命题“a∈A”的真值为“假”，相应的，命题“a∉A”的真值为“真”。
    • 因此，在处理集合之间的关系时，也可以借用命题的相关理论和方法进行分析和处理。

• （2）集合的基数

  • 集合的基数表示集合中元素的个数。
  • 定义3.2 集合的基数 一个集合中的元素个数称为集合的基数。集合A的基数用或表示。
• （3）集合的分类
  • 按集合中元素个数是否有限来进行分类，可将集合分为有限集和无限集两种。
  • 如果组成一个集合的元素个数是有限的，则称该集合为有限集合，简称有限集，否则称为无限集合，简称无限集。
  • 例如，英语字母组成的集合就是有限集，实数组成的集合就是无限集。

3.1.2集合的表示

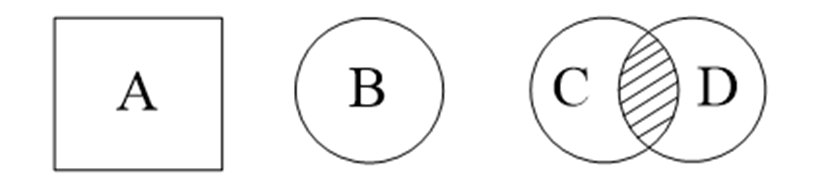
表示一个集合的主要方法有枚举法、描述法、图形法等3种： （1）枚举法 将集合的元素全部列出在花括号内，元素之间用逗号隔开，这种表示集合的方法称为枚举法。例如： A = {1，2，3，4，5} B= {3，2，1，4，5} C= {a，b，c，d} D= {a，c，d，d，b，a，c} 用枚举法表示集合时，如果集合的元素个数过多（甚至无限多个），那么，在能明显描述元素的规律时，也可以用省略号来代替所有未列出的元素。 （2）描述法 集合的描述法是通过刻画集合中元素所具备的某种特性来表示集合，通常用符号P(x)表示不同对象x所具有的性质或属性P，又称为属性表示法。集合的描述法可表示为： A= {x| P(x)} 上式表示集合A是由满足特性P的全体成员x组成。 （3）图形法 图形法是利用平面上的点所对应元素的封闭区域对集合进行图解标示。通常情况下可以省略封闭区域内的点，而仅用平面上的方形或圆形来表示集合，该方法又称为文氏图法。文氏图表示集合的方法如图3.1所示。

3.1.3特殊集合