ALU

74LS181 ALU 功能介绍_logic923的博客-CSDN博客_74ls181 74LS181**工作环境**

win10家庭版
QuartusII13.0

功能介绍
简介
74LS181 ALU是主要进行算术和逻辑运算的电路，可以作为处理器进行运算的核心部件。它对两个4位操作数进行逻辑或者算术运算等。74LS181在QuartusII中是一个老式74元件库中，它可以与74LS182级连为先行进位加法器。

引脚介绍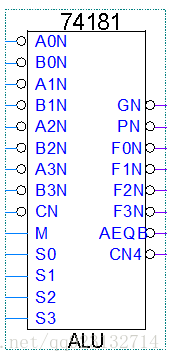
模型机用的芯片 - 图1
74ls181芯片总共有22个引脚。

数据引脚

8个数据输入端，A0m、A1n、A2n、A3n，B0n、B1n、B2n、B3n，（其中A3和B3是高位）。
4个二进制输出端F0、F1、F2、F3，以四位二进制形式输出运算的结果。
CN端处理进入芯片前进位值，CN4记录运算后的进位。
GN先行进位产生端。PN先行进位传递函数。

控制引脚

4个控制端，S0、S1、S2、S3，控制两个四位输入数据的运算，例如加、减、与、或。
M控制芯片的运算方式，包括算术运算和逻辑运算。

功能表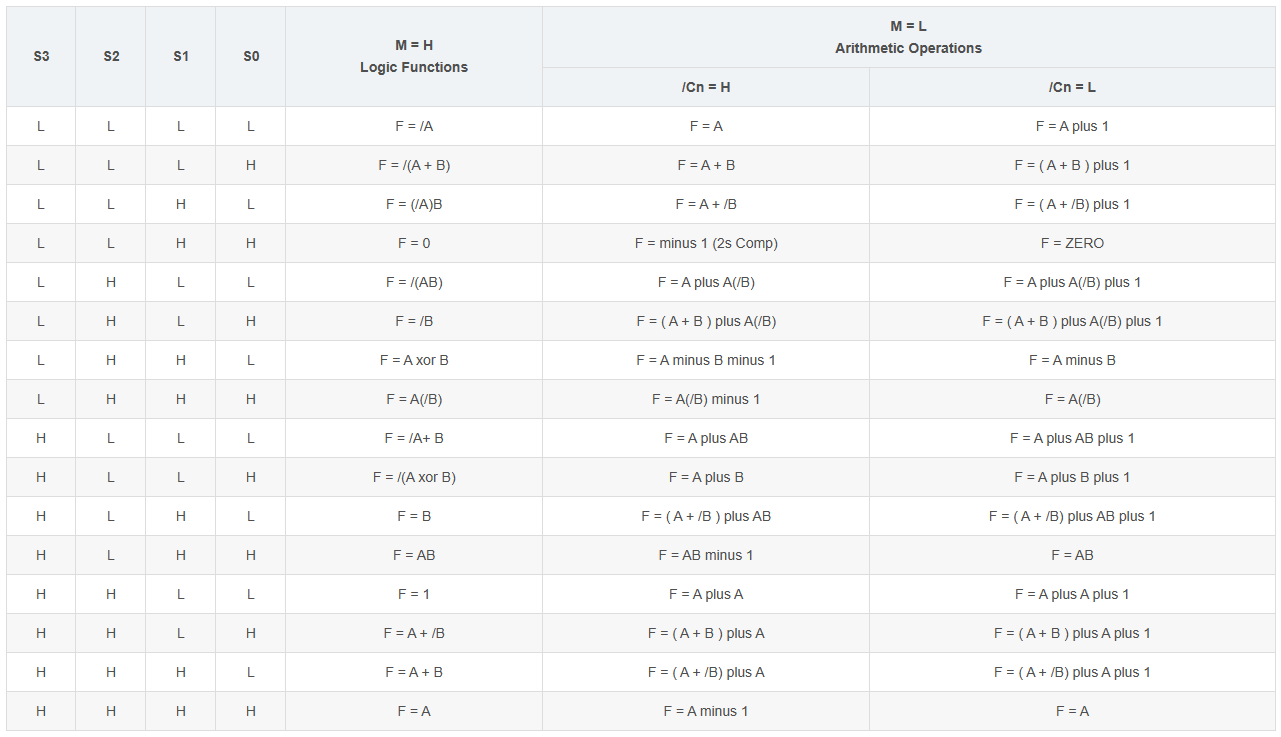

注：+ 是或的意思 /是非 plus是加 xor是异或

AR/IR

74LS273 八D型触发器功能介绍_logic923的博客-CSDN博客_8d触发器 74LS273**工作环境**
win10家庭版
QuartusII13.0

功能介绍
简介

触发器是一个具有记忆功能的，具有两个稳定状态的信息存储器件，是构成多种时序电路的最基本逻辑单元，也是数字逻辑电路中一种重要的单元电路。百度百科-D触发器

引脚介绍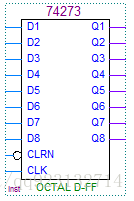
模型机用的芯片 - 图3
74LS273芯片总共有18个引脚。

数据引脚

8个数据输入端，D1、D2、D3、D4、D5、D6、D7、D8，（其中D8是高位）。
8个输出端Q1、Q2、Q3、Q4、Q5、Q6、Q7、Q8，以8位二进制形式输出运算的结果。

控制引脚

CLRN清零端
CLK时钟

功能表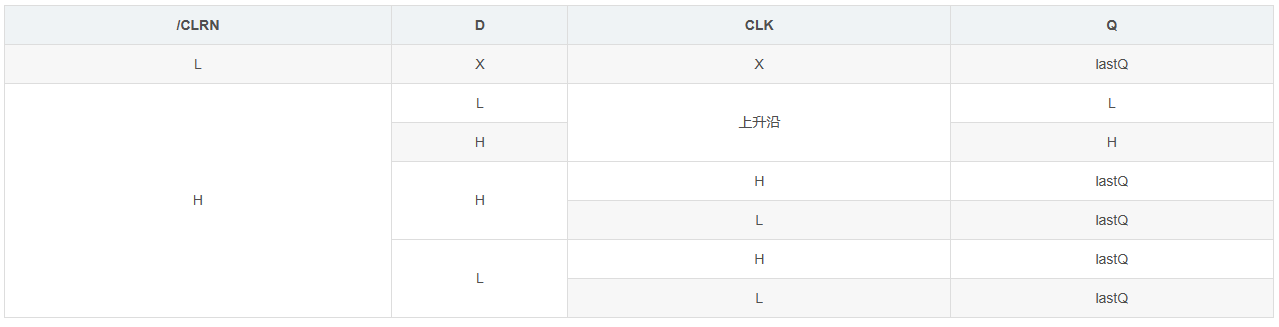

74LS194计数器及其应用 74LS194

74LS194功能特征

根据上面的描述，需要重点考虑的是置位、左移、右移、保持功能（异步清零不受时钟控制），一个时刻只能执行一个功能，需要一个4选1的选择器，确定执行什么功能。其电路图下图1所示（具体的功能可自行分析）：
图1:74LS194电路图（未包含异步清零），摘自维库

其中，S1和S0是控制端，对应的功能描述如下图2所示：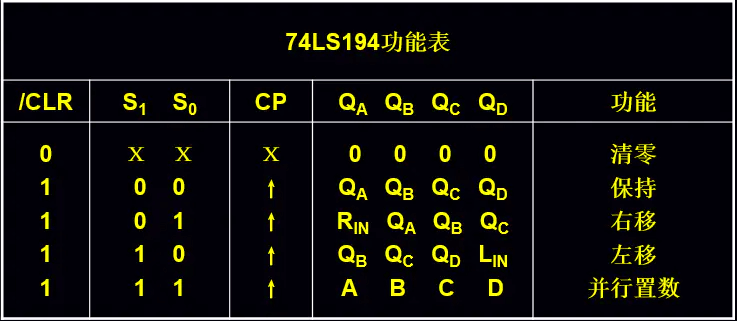
图2：74LS194功能描述

对应的逻辑符号如下图3所示：
图3:74LS194逻辑符号

74LS194应用

用194可以做很多事情，如典型的环形移位器、扭环形移位器，其逻辑图如下图4所示：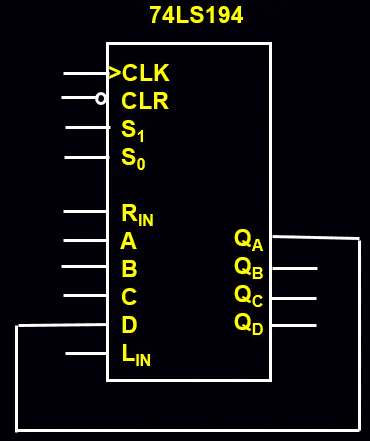
图4：环形移位器

如果把图4中的QA的输出变为非，则为扭环形移位器。
当然，也可以利用194完成串行数据到并行数据的转换（这种转换的本质是：输入数据一位一位读取，而输出数据则一次读取），如下图5所示：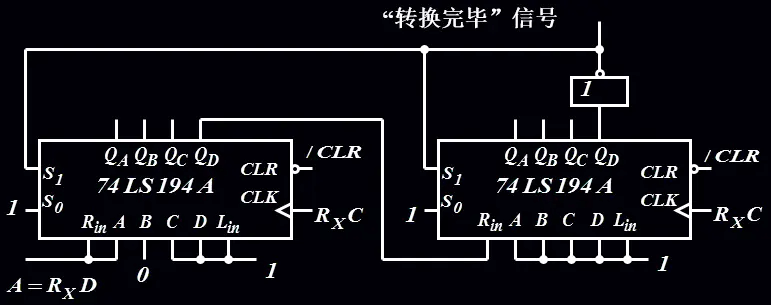
图5：串行数据到并行数据的转换

分析图5，由于S0值始终为1，S1S0有两种取值，一种为11，一种为01，当为11时，做置位操作，当为01时，做右移操作，具体分析如下（假设RxD的数据为A7A6A5A4A3AA2A1，A7先输入）：

step1：初始时，同时清零，此时右边的194的QD为0，经过一个非门后，取值为1，导致S1S0为11，做置位操作，置位为：A70111111;
step2：当时钟脉冲来临时，由于右边的194的QD为1，此时S1S0取值为01，实现右移，其状态迁移序列为：

A70111111 —> A6A7011111 —> A5A6A701111 —> A4A5A6A70111 —> A3A4A5A6A7011 —> A2A3A4A5A6A701 —> A1A2A3A4A5A6A70
step3：当时钟脉冲再来是，由于右边的194的QD为0，S1S0取值为11，进行置位，回到Step2，进入状态迁移循环。

小结
74LS194是相对较为灵活的一个电子器件，既可完成左移，又可完成右移，功能相对较为完善，广泛应用于电路设计中。

PC

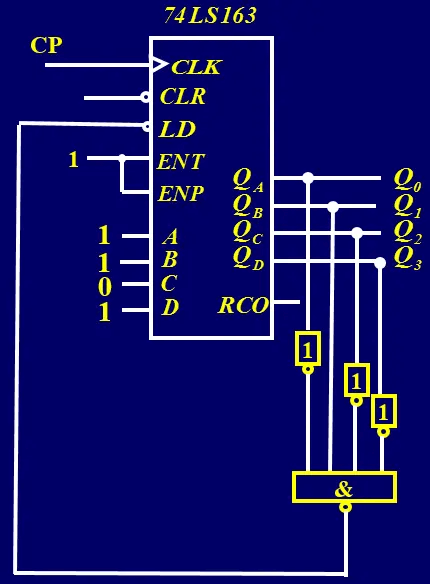
74LS163计数器及其应用 74LS163计数器

74LS163计数器

74LS163计数器有5个控制端、4个数据输入端和5个输出端，其逻辑功能和对应的逻辑符号如下图1和图2所示：

图1：74LS163功能表

图2：74LS163的逻辑符号
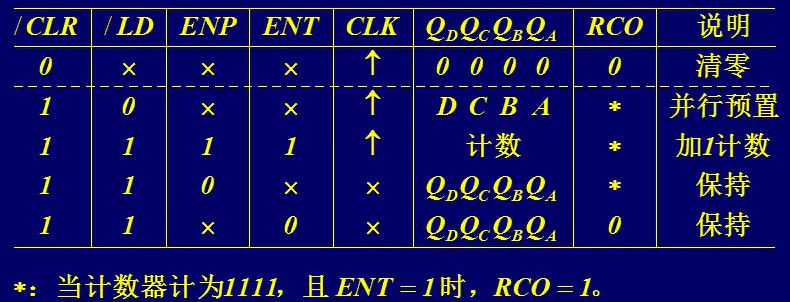
RCO表示进位，其语义为：当从0000~1111计满一轮，并且ENT为1时，RCO为1，其它时候均为0.
由图1，74LS163具有置位、保持、加1计数等功能，在这些功能的基础上，可以完成相对复杂的电路。

例1：以74LS163为基础设计一个6分频电路

首先，需要明白什么叫分频，图3展示了分频的效果：

图3：74LS163的波形图
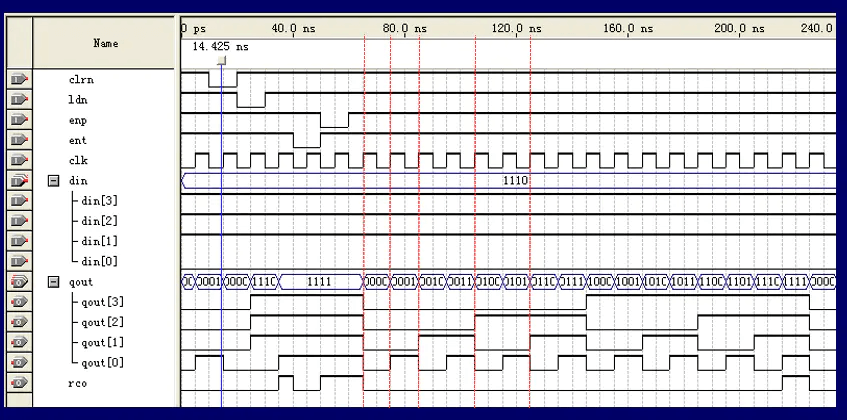
分频通常以CP（时钟脉冲）为基础，从图3中可以看出：qout[0]的周期为CP的2倍，qout[1]的周期为CP的4倍，qout[2]位8倍，qout[3]为16倍，显然，其频率分别为CP的1/2, 1/4, 1/8, 1/16，即所谓的2-分频，4-分频，8-分频，16-分频。
再进一步分析，对于qout[0]，其变化为：当一个时钟脉冲来临时，qout[0]变化一次；对于qout[1]，每两个时钟脉冲，qout[1]值变化一次；对于qout[2]，每四个时钟脉冲，qout[2]值变化一次；对于qout[3]，每8个时钟脉冲，qout[3]值变化一次。依次类推，如果要做6分频，显然应该是每3个时钟脉冲，值变化一次，如何用74LS163来做6-分频呢？
显然，这个问题变为：如何使74LS163中的某一位每3个时钟脉冲跳变一次。显然，只有QD和QC这两位的变化可能满足（QB每两个脉冲跳变一次，QA每个脉冲跳变一次），如果选择QC，显然可以找出一个序列：
0000 —-> 0001 —-> 0010 —-> 1101 —-> 1110 —->1111 —->0000 —-> …
对于QC，先是3个0，然后是3个1，开始循环，正好是6分频。仔细观察，发现这个循环对于QD也是6分频。
针对上面分析得到的状态迁移序列，如何用74LS163来实现呢？对于前半部0000 —-> 0001 —-> 0010，执行的是正常的计数功能，对于后半部1101 —-> 1110 —->1111（ —->0000），执行的也是正常的计数功能，只有0010 —-> 1101是一个跳跃，即当计数器状态为0010时，下一个状态需要用到163计数器的并行置数功能，因此，需要对163的计数器的输出进行判断，当输出为0010时，用1101对电路进行置数（确保下一时刻电路状态为1101）。
在此分析的基础上，其电路图如图4所示：

图4:6-分频电路

例2:2421码的模8电路

假设要求模8的状态序列如下图5所示：

图5:2421码模8状态迁移图
在图5中，模8的状态迁移序列为:

0001 —-> 0010 —-> 0011 —-> 0100 —-> 1011 —-> 1100 —-> 1101 —-> 1110 —-> 0001 —-> …
即：初始状态为0001，当状态为1110时，一轮计满并迁移到状态0001。

这个状态迁移序列中，需要注意的地方包括：

初始状态为0001，即初始时需要置位
序列前半部分 0001 —-> 0010 —-> 0011 —-> 0100和序列后半部分1011 —-> 1100 —-> 1101 —-> 1110执行的是正常的计数功能
0100 —-> 1011有状态跳跃，在到达状态0100时，需要置数；1110 —-> 0001，即记录一轮满时，需要置数

从上面的分析中得知，这个电路中存在两次置数，一次为初始状态的置数，另一个则为0100 —-> 1011状态迁移时的置数，并且两次需要置的数值是不一样的，其它情况正常计数。因此，置数的时候需要作二选一，即从两个数中选择一个置数，需要一个二选一的选择器；另外，还要确定置数的时机，显然，当状态为1110时，需要置数为0001，当状态为0100时，需要置数为1011。
由上分析可知，其对应的电路图如图6所示：
图6:2421码模8计数器

小结

上面两个例子都是相对较难的例子，需要综合前面学习的组合电路，要求对组合电路和时序电路的基本功能非常熟悉。其基本思路相对而言，比较明晰，把需要跳转的状态找出来，然后需要置位的状态进行相应的设置即可。