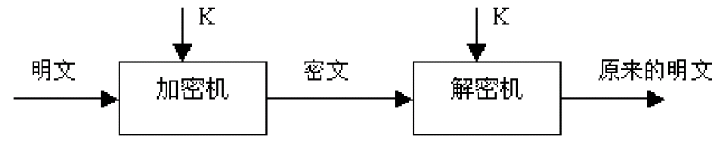
单密钥系统的加密密钥和解密密钥相同,或实质上等同,即从一个易于得出另一个,如下图所示。
对称密码算法(symmetric cipher):
- DES(Data Encryption Standard)
- Triple DES
- IDEA
- AES
- RC5
- CAST-128
- 。。。。。。
分组密码算法(Block Cipher)
特点
- 明文被分为固定长度的块,即分组,分组一般为64比特,或者128比特
- 对每个分组用相同的算法和密钥加/解密
- 密文分组和明文分组同样长
分组密码原理
分组密码是将明文消息编码表示后的数字(简称明文数字)序列,划分成长度为n的组(可看成长度为n的矢量),每组分别在密钥的控制下变换成等长的输出数字(简称密文数字)序列。

分组密码的一般设计原理
- 加密函数:V×K→V,n是n维矢量空间,K为密钥空间。
- 在相同的密钥k的控制下,加密函数可看成是函数E(ο,K): V→V,这实质上是对字长为n的数字序列的置换。
- 分组加密器本质上就是一个巨大的替换器,在密钥的控制下,能从一个足够大和足够好的置换子集中简单而迅速地选出一个置换,用来对当前输入的明文数字组进行加密变换。
- 采用了乘积加密器的思想,即轮流使用替代和置换
- Shannon提出的设计密码系统的两种基本方法:扩散和混淆。Shannon认为,在理想密码系统中,密文的所有统计特性都应与使用的密钥独立。
扩散
要求明文的统计特征消散在密文中。即让明文的每个比特影响到密文的许多比特的取值。尽可能使明文和密文的统计关系变复杂。
混淆
使密文与密钥之间的统计关系尽量复杂,以阻止攻击者发现密钥。
- 扩散和混淆的目的都是为了挫败推测出密钥的尝试,从而抗击统计分析。
- 迭代密码是实现混淆和扩散原则的一种有效的方法。
- 迭代密码是实现混淆和扩散原则的一种有效的方法。合理选择的轮函数经过若干次迭代后能够提供必要的混淆和扩散。
- 分组密码由加密算法、解密算法和密钥扩展算法三部分组成。解密算法是加密算法的逆,由加密算法惟一确定,因而我们主要讨论加密算法和密钥扩展算法。
分组密码的一般结构—Feistel网络结构
- Feistel网络是由Horst Feistel在设计Lucifer分组密码时基于扩散和扰乱的思想所发明的,并因被DES采用而流行。
- 现在正在使用的几乎所有重要的对称分组密码都使用这种结构,如FEAL、Blowfish等。
Feistel密码结构的设计动机
- 分组密码对n比特的明文分组进行操作,产生出一个n比特的密文分组,共有2n个不同的明文分组,每一种都必须产生一个唯一的密文分组,这种变换称为可逆的或非奇异的。
- | 可逆映射 | | | | 不可逆映射 | | —- | —- | —- | —- | —- | | 00 | 11 | | 00 | 11 | | 01 | 10 | | 01 | 10 | | 10 | 00 | | 10 | 01 | | 11 | 01 | | 11 | 01 |
- n = 4时的一个普通代换密码的结构

Feistel网络结构原理
一个分组长度为n (偶数)比特的L轮Feistel网络的加密过程如下:
- 给定明文P,将P分成左边和右边长度相等的两半并分别记为L 和R,从而P = LR,进行L轮完全类似的迭代运算后,再将左边和右边长度相等的两半合并产生密文分组。
- 每一轮i从以前一轮得到的L和R为输入,另外的总输入还有从总的密钥K生成的子密钥K。
其中L和R的计算规则如下:
- L = R; R = L ⊕F(R,K)
- 在第L轮迭代运算后,将L和R再进行交换,输出C = RL
- 其中F是轮函数,K是由种子密钥K生成的子密钥

- 一般结构
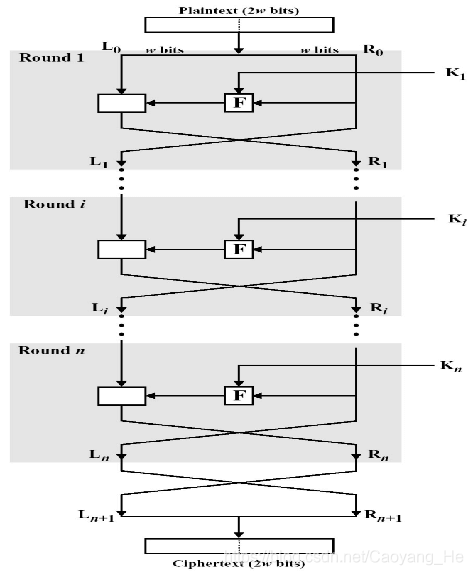
Feistel网络的安全性和软、硬件实现速度取决于下列参数:
- 分组长度:分组长度越大则安全性越高(其他条件相同时),但加、解密速度也越慢。64比特的分组目前也可用,但最好采用128比特。
- 密钥长度:密钥长度越大则安全性越高(其他条件相同时),但加、解密速度也越慢。64比特密钥现在已不安全,128比特是一个折中的选择。
- 循环次数:Feistel网络结构的一个特点是循环次数越多则安全性越高,通常选择16次。
Feistel网络的安全性和软、硬件实现速度取决于下列参数:
- 子密钥算法:子密钥算法越复杂则安全性越高。
- 轮函数:轮函数越复杂则安全性越高。
- 快速的软件实现:有时候客观条件不允许用硬件实现,算法被镶嵌在应用程序中。此时算法的执行速度是关键。
- 算法简洁:通常希望算法越复杂越好,但采用容易分析的却很有好处。若算法能被简洁地解释清楚,就能容易通过分析算法而知道算法抗各种攻击的能力,也有助于设计高强度的算法。
Feistel网络解密过程
- Feistel网络解密过程与其加密过程实质是相同的。
- 以密文分组作为算法的输入,但以相反的次序使用子密钥,即- 第一轮使用K,第二轮使用K,直至第L轮使用K,这意味着可以用同样的算法来进行加、解密。
- 先将密文分组C = RL,分成左边和右边长度相等的两半,分别记为L和R,根据下列规则计算 L R
L = R ,R = L ⊕ F (R ,K) 1≤i≤L - 最后输出的分组是RL
数据加密标准(DES)
数据加密标准(Data Encryption Standard,DES)是至 今为止使用最为广泛的加密算法。
1974年8月27日, NBS开始第二次征集,IBM提交了算法LUCIFER,该算法由IBM的工程师在1971~1972年研制。
1975年3月17日, NBS公开了全部细节1976年,NBS指派了两个小组进行评价。
1976年11月23日,采纳为联邦标准,批准用于非军事场合的各种政府机构。
1977年1月15日,“数据加密标准”FIPS PUB 46发布
规定每隔5年由美国国家保密局(National Security Agency)重新评估它是否继续作为联邦加密标准。
最近的一次评估是在1994年1月,当时决定1998年12月以后,DES不再作为联邦加密标准。新的美国联邦加密标准被称为高级加密标准AES ( Advanced Encryption Standard )。
DES对推动密码理论的发展和应用起到了重大的作用,学习 和研究它,对于掌握分组密码的基本理论、设计思想和实际应用仍然有着重要的参考价值。
DES加密的主要步骤和操作
DES背景
数据加密标准(Data Encryption Standard,DES)是至 今为止使用最为广泛的加密算法。
1974年8月27日, NBS开始第二次征集,IBM提交了算法LUCIFER,该算法由IBM的工程师在1971~1972年研制。
1975年3月17日, NBS公开了全部细节1976年,NBS指派了两个小组进行评价。
1976年11月23日,采纳为联邦标准,批准用于非军事场合的各种政府机构。
1977年1月15日,“数据加密标准”FIPS PUB 46发布
规定每隔5年由美国国家保密局(National Security Agency)重新评估它是否继续作为联邦加密标准。
最近的一次评估是在1994年1月,当时决定1998年12月以后,DES不再作为联邦加密标准。新的美国联邦加密标准被称为高级加密标准AES ( Advanced Encryption Standard )。
DES对推动密码理论的发展和应用起到了重大的作用,学习 和研究它,对于掌握分组密码的基本理论、设计思想和实际应用仍然有着重要的参考价值。
DES的变形
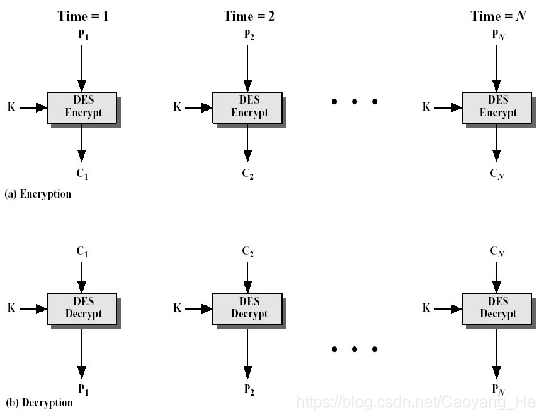
双重DES
最简单的多次加密形式有两个加密阶段和两个密钥,给定一个明文P和两个加密密钥K1和K2,有:
C = E(E(/P)) ←→ P = D(D(/C))
对于DES来说,密钥长度56×2=112

双密钥的三重DES
一个用于对付中途攻击的明显方法是用3个密钥进行三个阶段的加密,这样要求一个56×3=168bit的密钥,这个密钥有点过大。
作为一种替代方案,Tuchman提出使用两个密钥的三重加密方法。这个加密函数采用一个加密-解密-加密序列:
C=E(D(E(/P))) ←→ P=D(E( D(/C)))。

具体细节
https://blog.csdn.net/Caoyang_He/article/details/88868493
AES加密的主要步骤和操作
AES背景
1997年4月15日,美国国家标准技术研究(NIST)发起征集高级加密标准(Advanced Encryption Standard)AES的活动,活动目的是确定一个非保密的、可以公开技术细节的、全球免费使用的分组密码算法,作为新的数据加密标准。
1997年9月12日,美国联邦登记处公布了正式征集AES候选算法的通告。基本要求是:比三重DES快、至少与三重DES一样安全、数据分组长度为128比特、密钥长度为128/192/256比特。
1998年8月12日,在首届AES会议上指定了15个候选算法。
1999年3月22日第二次AES会议上,将候选名单减少为5个,这5个算法是RC6,Rijndael,SERPENT,Twofish和MARS。
2000年4月13日,第三次AES会议上,对这5个候选算法的各种分析结果进行了讨论。
2000年10月2日,NIST宣布了获胜者—Rijndael算法,2001年11月出版了最终标准FIPS PUB197
AES的总体描述
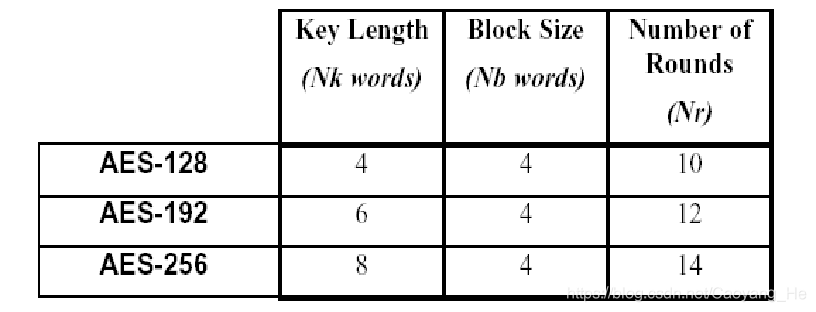
AES具有128bit的分组长度,三种可选的密钥长度,即128bit、192bit和256bit。AES是一个迭代型密码;轮数Nr依赖于密钥长度。密钥为128bit、192bit、256 bit时,轮数分别为:10、12、14。算法执行过程如下:
- 给定一个明文x,将State初始化为x,并进行AddRoundKey操作,将RoundKey和State异或。
- 对前Nr-1轮中的每一轮,用S盒对进行一次代换操作,称为SubBytes;对State做一置换ShiftRows;再对State做一次操作MixColumns;然后进行AddRoundKey操作。
- 依次进行SubBytes、 ShiftRows和AddRoundKey操作。
- 将State定义为密文。
AES的参数
具体细节
https://blog.csdn.net/Caoyang_He/article/details/88868493
分组密码的工作模式
含义
分组密码在加密时明文分组的长度是固定的,而实用中待加密消息的数据量是不定的,数据格式可能是多种多样的。为了能在各种应用场合安全地使用分组密码,通常 对不同的使用目的运用不同的工作模式。
一个分组密 码的工作模式就是以该分组密码为基础构造的一个密码系统。
目前已提出许多种分组密码的工作模式,如电码本(ECB)、密码分组链接(CBC)、密码反馈(CFB)、输 出反馈(OFB)、级连(CM)、计数器、分组链接(BC)、扩散密码分组链接(PCBC)、明文反馈(PFB) 、非 线性函数输出反馈(OFBNLF)等模式。
PS:提出分组密码的工作模式就是为了让同一个分组的明文加密后的密文不同,从而避免统计攻击
ECB(Electronic Codebook)模式
ECB(Electronic Codebook)模式是最简单的运行模式,它一次对一个64比特长的明文分组加密,而且每次的加密密钥都相同
概念图
优点
- 实现简单
- 不同明文分组的加密可并行实施,尤其是硬件实现时速度很快
缺点
不同的明文分组之间的加密独立进行,造成相同明文分组对应相同密文分组,因而不能隐蔽明文分组的统计规律和结构规律,不能抵抗替换攻击。
典型应用
- 用于随机数的加密保护;
- 用于单分组明文的加密。
实例
例: 假设银行A和银行B之间的资金转帐系统所使用报文模式如下

敌手C通过截收从A到B的加密消息,只要将第5至第12分组替换为自己的姓名和帐号相对应的密文,即可将别人的存款存入自己的帐号。
密码分组链接(CBC-Cipher Block Chaining)模式
每次加密使用同一密钥,加密算法的输入是当前明文前一次密文组的异或。因此加密算法的输入与明文分组之间 不再有固定的关系,所以重复的明文分组不会在密文中暴露。
概念图
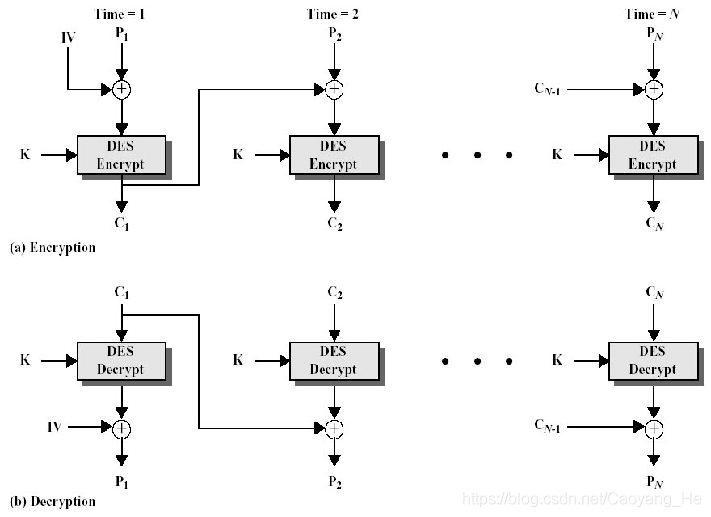
特点
- 明文块的统计特性得到了隐蔽。
由于在密文CBC模式中,各密文块不仅与当前明文块有关,而且还与以前的明文块及初始化向量有关,从而使明文的统计规律在密文中得到了较好的隐蔽。 - 具有有限的(两步)错误传播特性。
一个密文块的错误将导致两个密文块不能正确脱密。 - 具有自同步功能
密文出现丢块和错块不影响后续密文块的脱密。若从第t块起密文块正确,则第t+1个明文块就能正确求出。 - 明文分组中一位出错,将影响该分组的密文及其以后的所有密文分组
典型应用
- 数据加密;
- 完整性认证和身份认证;
完整性认证的含义
完整性认证是一个“用户”检验它收到的文件是否遭到第三方有意或无意的篡改。
实例
例:电脑彩票的防伪技术
方法:
- 选择一个分组密码算法和一个认证密钥,存于售票机内
- 将电脑彩票上的重要信息,如彩票期号、彩票号码、彩票股量、售票单位代号等重要信息按某个约定的规则作为彩票资料明文
- 对彩票资料明文扩展一个校验码分组后,利用认证密钥和分组密码算法对之加密,并将得到的最后一个分组密文作为认证码打印于彩票上面;
认证过程:
执行3),并将计算出的认证码与彩票上的认证码比较,二者一致时判定该彩票是真彩票,否则判定该彩票是假彩票。
CFB(Cipher Feedback)模式:
若待加密消息需按字符、字节或比特处理时,可采用CFB模式。并称待加密消息按 j 比特处理的CFB模式为 j 比特CFB模式。
适用范围
适用于每次处理 j比特明文块的特定需求的加密情形,能灵活适应数据各格式的需要。
概念图
加密

解密

优点
- 这是将分组密码当作序列密码(数据以位或者字节形式到达)使用的一种方式,
- 加密、解密都需要用到分组加密器;
- 明文发生错误,错误会传播;
- 如果密文发生传输错误,只会影响它出现在移位寄存器期间解密的8个字节的数据得不到正确解密,8个字节一过,后面明文可以得到正确的解密结果。
缺点
比较浪费,因为每轮加解密中都丢弃了大部分结果,通常只保留了的S为为1个字节。
OFB (Output Feedback)模式
OFB 模式在结构上类似于CFB。不同之处
- OFB模式将加密算法的输出反馈到移位寄存器,而CFB模式是将密文单元反馈到移位寄存器。
- OFB针对明文和密文分组运算,而CFB仅对S位的子集运算
概念图
加密

解密

优点
- 传输过程中的比特错误不会被传播。
例如C1中出现一比特错误,在解密结果中 只有P1受影响,以后各明文单元则不受影响 。而在CFB中, C1也作为移位寄存器的输入,因此它的一比特错误会影响解 密结果中各明文单元的值。
解密中密文的1比特也只影响明文的1个错误 - 分组密码转化为流模式;
- 可以及时加密传送小于分组的数据;
缺点
难于检测密文是否被篡改。
适用于传输语音图像
计数器模式CTR(Counter)
对一系列输入数据块(称为计数)进行加密,产生一系列的输出块,输出块与明文异或得到密文。
应用于ATM网络安全及IPSec中
密码算法产生一个16 字节的伪随机码块流,伪随机码块与输入的明文进行异或运算后产生密文输出。密文与同样的伪随机码进行异或运算后可以重产生明文。
概念图
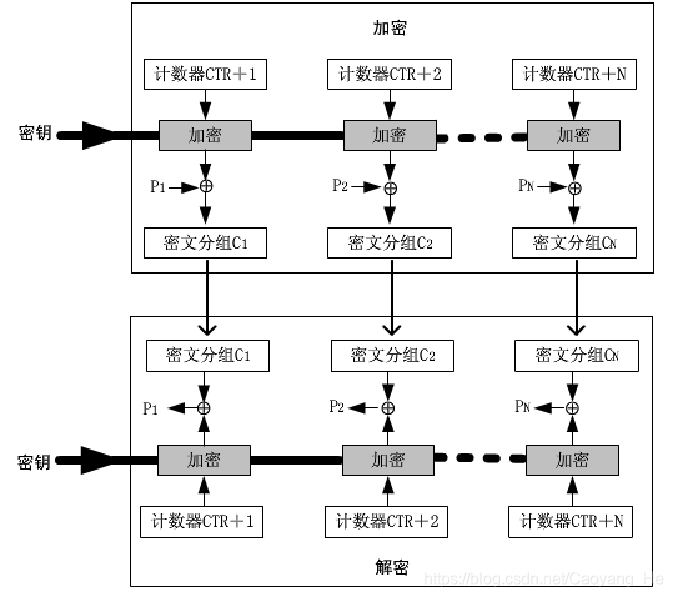
CTR的特点
- 使用与明文分组规模相同的计数器长度
- 处理效率高(并行计算)
- 预处理可以极大提高吞吐量:算法和加密盒的输出不依靠明文和密文的输入
- 可以随机对任意一个密文分组进行解密处理,对该密文分组的处理与其他密文无关(第i块解密不依赖第i-1块)
- 实现的简单性,只是异或,且无解密算法
- 适用于实时性和速度要求较高的场合
总结
| 模式 | 描述 | 典型应用 |
|---|---|---|
| 电码本(CBC) | 用相同的密钥分别对明文分组独立加密 | 单个数据的安全传输(如一个加密密钥) |
| 密文分组链接(CBC) | 加密算法的输入是上一个密文组和下一个明文组的异或 | 面向分组的通用传播 认证 |
| 密文反馈(CFB) | 一次处理s位,上一块密文作为加密算法的输入,产生的伪随机数输出与明文异或作为下一个单元的密文 | 面向数据流的通用传播 认证 |
| 输出反馈(OFB) | 与CFB类似,只是加密算法的输入是上一次加密的输出,且使用整个分组 | 噪声信道上的数据流传输(如卫星通信) |
| 计数器(CTR) | 每个明文分组都与一个经过加密的计数器相异或。对每个后续分组计数器递增 | 面向分组的通用传播 用于高速需求 |
流密码
每次可加密一个比特或一个字节
适合比如远程终端输入加密类的应用
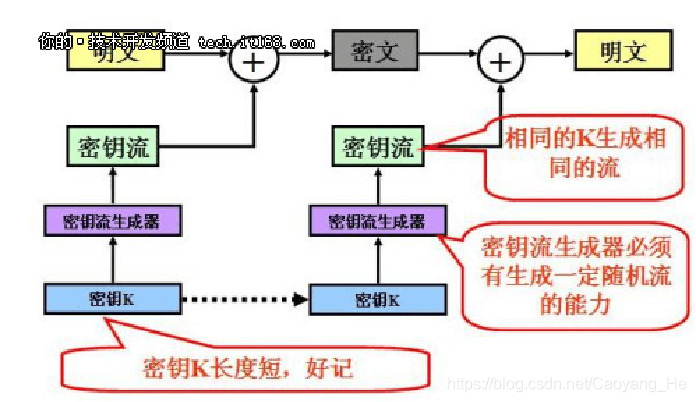
RC4
简介
RC4由RSA三人组中的头号人物Ronald Rivest在1987年设计的密钥长度可变的流加密算法簇。
和DES算法一样,是一种对称加密算法。
算法的速度可以达到DES加密的10倍左右,且具有很高级别的非线性 。
可变密钥长度,可变范围为1-256字节(8-2048比特)
以随机置换为基础。密钥长度是可变的,RC4起初是用于保护商业机密的。但是在1994年9月,它的算法被发布在互联网上,也就不再有什么商业机密了
用途广泛,常用于SSL/TLS,IEEE 802.11无线语句网标准的一部分WEP(Wired Equivalent Privacy)协议和新Wifi受保护访问协议(WPA)中。
相关概念
- 密钥流:RC4算法的关键是根据明文和密钥生成相应的密钥流,密钥流的长度和明文的长度是对应的,也就是说明文的长度是500字节,那么密钥流也是500字节。当然,加密生成的密文也是500字节,因为密文第i字节=明文第i字节^密钥流第i字节;
- 状态向量S:长度为256,S[0],S[1]…..S[255]。每个单元都是一个字节,算法运行的任何时候,S都包括0-255的8比特数的排列组合,只不过值的位置发生了变换;
- 临时向量T:长度也为256,每个单元也是一个字节。如果密钥的长度是256字节,就直接把密钥的值赋给T,否则,轮转地将密钥的每个字节赋给T;
- 密钥K:长度为1-256字节,注意密钥的长度keylen与明文长度、密钥流的长度没有必然关系,通常密钥的长度趣味16字节(128比特)。
概念图
伪代码
第一部分:初始化算法(KSA)
- 初始化S和T
for i=0 to 255 do
S[i]=i;
T[i]=K[ i mod keylen ]; - 初始排列S
j=0;
for i=0 to 255 do
j= ( j+S[i]+T[i])mod256;
swap(S[i],S[j]);
第二部分:伪随机子密钥流生成算法
- 产生密钥流
i,j=0;
for r=0 to len do //r为明文长度,r字节
i=(i+1) mod 256;
j=(j+S[i])mod 256;
swap(S[i],S[j]);
t=(S[i]+S[j])mod 256;
k[r]=S[t];

