密码学的基本概念
密码学(Cryptology):
研究信息系统安全保密的科学。
密码编码学(Cryptography):
研究对信息进行编码,实现对信息的隐蔽。
密码分析学(Cryptanalytics) :
研究加密消息的破译或消息的伪造。
消息被称为明文(Plaintext)。
用某种方法伪装消息以隐藏它的内容的过程称为加密(Encrtption),被加密的消息称为密文(Ciphertext),而把密文转变为明文的过程称为解密(Decryption)。
密码算法:
用于加密和解密的数学函数。
密码员对明文进行加密操作时所采用的一组规则称作加密算法(Encryption Algorithm)。\所传送消息的预定对象称为接收者(Receiver)。接收者对密文解密所采用的一组规则称为*解密算法(Decryption Algorithm)。
加密过程
密码学的目的:Alice和Bob两个人在不安全的信道上进行通信,而破译者Oscar不能理解他们通信的内容。
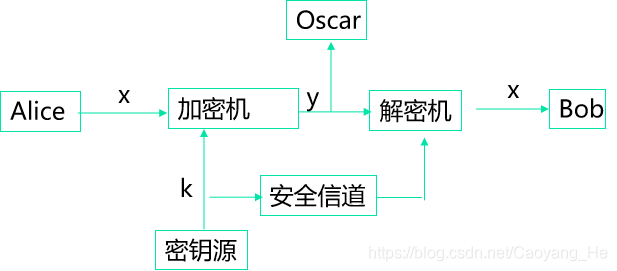
加密和解密算法的操作通常都是在一组密钥的控制下进行的,分别称为加密密钥(Encryption Key) 和解密密钥(Decryption Key)。
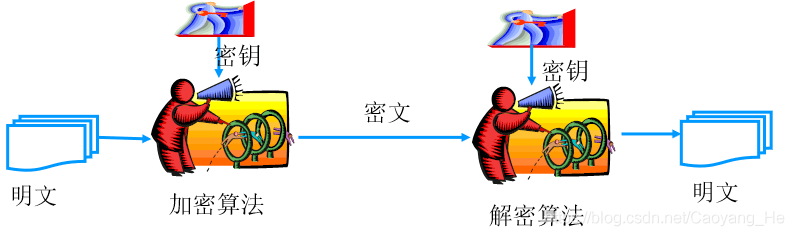
密码体制
一个五元组(P,C,K,E,D)满足条件:
- P是可能明文的有限集;(明文空间)
- C是可能密文的有限集;(密文空间)
- K是一切可能密钥构成的有限集;(密钥空间)
- 任意k∈K,有一个加密算法ek∈E和相应的解密算法dk∈D,使得ek : P→C和dk : C→P分别为加密解密函数,满足dk(ek(x))=x,其中 x ∈P。
加密算法基本原理
代替:明文中的元素映射成另一个元素
置换 :重新排列
要求:不允许信息丢失,即算法可逆
基于密钥的算法,按照密钥的特点分类:
对称密码算法(symmetric cipher):加密密钥和解密密钥相同,或实质上等同,即从一个易于推出另一个。又称秘密密钥算法或单密钥算法。
非对称密钥算法(asymmetric cipher):加密密钥和解密密钥不相同,从一个很难推出另一个。又称公开密钥算法(public-key cipher) 。
密码分析破解类型:
- 唯密文攻击
密码分析者仅知道有限数量用同一个密钥加密的密文 - 已知明文攻击
密码分析者除了拥有有限数量的密文外,还有数量限定的一些已知“明文—密文”对 - 选择明文攻击
密码分析者除了拥有有限数量的密文外,还有机会使用注入了未知密钥的加密机,通过自由选择明文来获取所希望的“明文—密文”对。 - 选择密文攻击
密码分析者除了拥有有限数量的密文外,还有机会使用注入了未知密钥的解密机,通过自由选择密文来获取所希望的“密文—明文”对。 - 选择文本攻击
密码的安全性
无条件安全(Unconditionally secure)
无论破译者有多少密文,他也无法解出对应的明文,即使他解出了,他也无法验证结果的正确性。(除一次一密钥,都不是无条件安全)
计算上安全(Computationally secure)
破译的代价超出信息本身的价值
破译的时间超出了信息的有效期
现代密码学基本原则
设计加密系统时,总假定密码算法是可以公开的,需要保密的是密钥。“一切秘密在于密钥之中,而加密算法可以公开” 即Kerckhoff原则。
密码学的起源和发展三个阶段:
1949年之前:密码学是一门艺术
古典密码(classical cryptography)
隐写术(steganography):不同于加密。
如果把一封信锁在保险柜中,把保险柜藏在纽约的某个地方…,然后告诉你去看这封信。这并不是安全,而是隐藏。
1949~1975年:密码学成为科学
计算机使得基于复杂计算的密码成为可能
1949年Shannon的“The Communication Theory of Secret Systems”
1967年David Kahn的《The Codebreakers》
1971-73年IBM Watson实验室的Horst Feistel等的几篇技术报告
Smith,J.L.,The Design of Lucifer, A Cryptographic Device for Data Communication, 1971
Smith,J.L.,…,An Expremental Application of Cryptogrphy to a remotely Accessed Data System, Aug.1972
Feistel,H.,Cryptography and Computer Privacy, May 1973
数据的安全基于密钥而不是算法的保密
1976年以后:密码学的新方向——公钥密码学
1976年Diffie & Hellman的“New Directions in Cryptography”提出了不对称密钥密码
1977年Rivest,Shamir & Adleman提出了RSA公钥算法
90年代逐步出现椭圆曲线等其他公钥算法
公钥密码使得发送端和接收端无密钥传输的保密通信成为可能!
1977年DES正式成为标准80年代出现“过渡性”的“post DES”算法,如IDEA,RCx,CAST等
90年代对称密钥密码进一步成熟 Rijndael,RC6, MARS,Twofish,Serpent等出现
2001年Rijndael成为DES的替代者
经典密码体制
代替密码(substitution cipher)
就是明文中的每一个字符被替换成密文中的另一个字符。接收者对密文做反向替换就可以恢复出明文。
简单代替密码(simple substitution cipher):
又称单字母密码(monoalphabetic cipher),明文的一个字符用相应的一个密文字符代替。
多字母密码(ployalphabetic cipher):
明文中的字符映射到密文空间的字符还依赖于它在上下文的位置。
恺撒密码(Caesar Cipher):
已知的最早(也是最简单的方式)的简单替代密码是朱里斯.恺撒所用的密码。恺撒密码是把字母表中的每个字母用该字母后面第3个字母进行代替。例如:
明文:meet me after the toga party
密文:PHHW PH DIWHU WKH WRJD SDUWS
既然字母表是循环的,因此Z后面的字母是A。能够通过列出所以可能性定义如下所示的变换:

移位密码(Shift cipher)
对每个明文字母p,恺撒加密可转化为移位密码,其中加密算法:
C = E(p) = (p+k) mod (26),其中k在1~25之间取值。
解密算法是:p = D(C) = (C-k) mod (26)
如果已知密文是恺撒密码,则使用强行攻击密码分析容易取得结果
直接对所有25个可能的密钥进行尝试。
模运算
a+b mod n = (a mod n+b mod n) mod n
a-b mod n = (a mod n-b mod n) mod n
a×b mod n = (a mod n×b mod n) mod n
仿射密码算法:
P = C = Z
K = (a,b) ∈K = Z×Z
加密
y = e(x) = (ax+b) mod 26
要求唯一解的充要条件:gcd(a,26)=1
解密
d (y) = (y – b) / a mod 26 = (y – b) a mod 26
仿射密码算法例:
K = (7,3),则有7 mod 26 = 15
因此对任一明文x有:e (x) = 7x + 3
解密:
d (y) = 15 * (y – 3) mod 26 = 15y – 19 mod 26
= 15 _ (7x + 3) – 19 = 105_x + 45 – 19
= 105x = x mod 26
仿射密码算法讨论:
首先,a = 1时,即是移位密码 (shift)
其次,如果K随意选择,可能会有问题
比如取K = (8,5) ,即y=8x+5 mod 26
明文a和n,记x = 0 (a),x = 13 (n),则y= 5,y = 5 (F)
不同的明文被加密成相同的密文,这样在解密时就有歧义
那么,如何避免这种歧义的出现?
合理选取密钥
要求a和26互素,即gcd (a, 26) = 1
如果k = (a,b)中a和26不互素则会有歧义,若a和26有公因子gcd (a, 26)=d>1,则对明文x=0和x =26/d的就相同密文
因为ax+b≡b mod 26,而ax+b=a×26/d+b=a/d×26+b≡b mod 26
即x1和x2被加密成相同的密文,所以解密时会混淆
这里,是否互素代表了什么性质呢?
互素才有“逆”
逆元,讨论在余数集合上进行
加法逆元:如果a + b≡0 mod n,互为加法逆元
则Zn中都有:0,0 1,n-1 2,n-2 … n/2,n/2
乘法逆元:如果a×b≡1 mod n,则a、b互为乘法逆元
如6×20≡1 mod 119
定义a的乘法逆元a,aa ≡ 1 mod n,显然可交换
由y = (ax + b) mod 26,
得x = d (y) = (y - b) / a = a (y - b) /aa = a (y - b)
即x = a(ax + b - b) = aax = x mod 26,x恢复了
乘法逆元如何构造?
3×9 ≡ 1 mod 26
5×?≡ 1 mod 26
并不是每个元素都有乘法逆元,概括为解方程 ax≡1 mod n
如何求乘法逆元:
一次同余方程ax ≡ b (mod m)这个方程有没有解,相当于问有没有那样一个整数x,使得对于某个整数y来说,有ax + my=b
推论:ax≡1 mod n有解 IFF (a, n) | 1,即a、n互素
欧几里德算法(求最大公约数):
基于定理:对于任何非负的整数a和非负的整数b:
gcd (a,b) = gcd (b,a mod b)
例如: gcd (55,22) = gcd (22,55 mod 22) = gcd (22,11) = 11
扩展欧几里德算法(求乘法逆元)例:
方式一
求7关于96的乘法逆元
| Q | X1 | X2 | X3 | Y1 | Y2 | Y3 |
|---|---|---|---|---|---|---|
| 1 | 0 | 96 | 0 | 1 | 7 | |
| 13 | 0 | 1 | 7 | 1-0*13=1 | 0–1*13= -13 | 96-7*13=5 |
| 1 | 1 | -13 | 5 | 0-1*1= -1 | 1- 1*(-13)= 14 | 7-1*5=2 |
| 2 | -1 | 14 | 2 | 1-2*0=1 | -13-2*14= -41 | 5-2*2=1 |
由于Y3=1,所以算法中止,故乘法逆元为-41 mod 96 = 55
即7×55 ≡1 mod 96
方式二
求22mod31的逆元
| i | r | q | x | y |
|---|---|---|---|---|
| -1 | 31 | 1 | 0 | |
| 0 | 22 | 0 | 1 | |
| 1 | 9 | 1 | 1 | -1 |
| 2 | 4 | 2 | -2 | 3 |
| 3 | 1 | 2 | 5 | -7 |
当r=1,则5x31+(-7)x 22 =1 mod 31
则逆元为(-7)+ 31 = 24
(PS:第一行为被除数,默认XY为 1 0 ,第二行为除数,默认XY为 0 1 个人觉得方式二好理解一些)

任意的单表代替密码算法:
设P=C=Z,K是由26个符号0,1,..,25的所有可能置换组成。任意π∈K,定义eπ(x)= π(x)=y 且d(y)=π(y)=x, π是π的逆置换。
注:
密钥空间K很大,|k|=26! ≈ 4×1026,破译者穷举搜索不行的(每微秒搜索加密一次需要6.4×1012年)。移位密码、乘数密码、仿射密码算法都是替换密码的特例。
任意的单表代替密码算法可由统计的方式破译
简单代替密码(simple substitution cipher):
又称单字母密码(monoalphabetic cipher),明文的一个字符用相应的一个密文字符代替。
多字母密码(ployalphabetic cipher):
明文中的字符映射到密文空间的字符还依赖于它在上下文的位置。
多字母代替密码:Playfair
Playfair:将明文中的双字母组合作为一个单元对待,并将这些单元转换为密文的双字母组合。
5×5变换矩阵: I与J视为同一字符
加密规则:按成对字母加密
相同对中的字母加分隔符(如x)
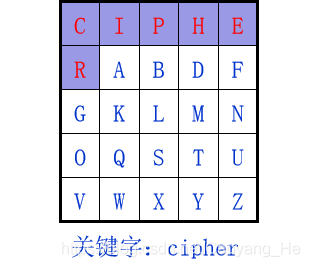
balloon ->ba lx lo on
同行取右边: he -> EC
同列取下边: dm -> MT
其他取交叉: kt > MQ,OD > TR
Hill密码:
基于矩阵的线性变换,由数学家Lester Hill于1929年研制
Z26上的线性变换
例:x=(x1,x2),y=(y1,y2)
 定义:y=11x+3x mod 26,y= 8x+7x mod 26
定义:y=11x+3x mod 26,y= 8x+7x mod 26
Vigenére密码:
是一种多表移位代替密码
设d为一固定的正整数,d个移位代换π=(π1,π2,…,πd) 由密钥序列K=(k1,k2,…,kd)给定,第i+td个明文字母由表i决定,即密钥ki决定
ek(xi+td) = (xi+td + ki) mod q = y,dk(yi+td) = (xi+td-ki) mod q = x
例子:q=26, x=polyalphabetic cipher, K=RADIO
明文 x= p o lya l phab e t i cc i pher
密钥 k= R ADIO RADIO RADIO RADIO
密文 y= GOOGO CPKTP NTLKQ ZPKMF
One-Time Pad一次一密:
Joseph Mauborgne提出使用与消息一样长且无重复的随机密钥来加密消息,密钥只对一个消息加解密,之后弃之不用;每条新消息都需要与其等长的新密钥,这就是一次一密,它是不可攻破的。
运算基于二进制数据而非字母
加密:ci = pi ⊕ ki, pi是明文第i个二进制位, ki是密钥第i个二进制位,ci是密文第i个二进制位, ⊕是异或运算
密文是通过对明文和密钥的逐位异或而成的,根据异或运算的性质,解密过程为pi = ci ⊕ ki,
给出任何长度与密文一样的明文,都存在着一个密钥产生这个明文。如果用穷举法搜索所有可能的密钥,会得到大量可读、清楚的明文,但是无法确定哪个才是真正所需的,因而这种密码不可破。
一次一密的两个限制
产生大规模随机密钥有实际困难
密钥的分配和保护无法保证
置换密码(permutation cipher)
又称换位密码(transposition cipher),明文的字母保持相同,但顺序被打乱了。
斯巴达密码棒
公元前405年,雅典和斯巴达之间的战争已进入尾声。斯巴达急需摸清波斯帝国的具体行动计划。斯巴达军队捕获了一名从波斯帝国回雅典送信的信使。可他身上除了一条布满希腊字母字样的普通腰带外,什么也没有。
斯巴达统帅把注意力集中到了那条腰带上,他反复琢磨那些乱码似的文字,却怎么也解不出来。最后当他无意中把腰带呈螺旋形缠绕在手中的剑鞘上时,原来腰带上那些杂乱无章的字母,竟组成了一段文字。它告诉雅典,波斯准备在斯巴达发起最后攻击时,突然对斯巴达军队进行袭击。
栅栏技术:
在这种密码中最简单的是栅栏技术,在该密码中以对角线顺序写下明文,并以行的顺序读出。
例如:以深度为2的栅栏密码加密消息“meet me after the toga party”,写出如下形式:
| m | e | m | a | t | r | h | t | g | p | r | y | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| e | t | e | f | e | t | e | o | a | a | t |
被加密的消息为:mematrhtgpryetefeteoaat
置换密码:
更为复杂的方式是以一个矩形逐行写出消息,再逐列读出该消息。
该方法以行的顺序排列。列的阶则成为该算法的密钥。密钥包含3方面信息::行宽、列高、读出顺序
例:
| key | 4 | 3 | 1 | 2 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| plaintext: | a | t | t | a | c | k | p |
| o | s | t | p | o | n | e | |
| d | u | n | t | i | l | t | |
| w | o | a | m | x | y | z |
ciphertext :TTNAAPTMTSUOAODWCOIXPETZ
完全保留字符的统计信息
使用多轮加密可提高安全性
Rotor Machines转轮密码机:
在现代密码系统出现之前,转轮密码机是最为广泛使用的多重加密器,尤其是在第二次世界大战中。
代表:German Enigma, Japanese Purple
转轮机使用了一组相互独立的旋转圆筒,可以通过电脉冲,每个圆筒有26个输入和26个输出,每个输入仅与一个输出相连,一个圆筒就定义了一个单表代换。
每按下一个键,圆筒旋转一个位置,内部连线相应改变,就定义了不同的单表代换密码,经过26个明文字母,圆筒回到初始状态,就得到一个周期为26的多表代换密码。
3个圆筒的转轮机就有263=17576个不同的代换字母表
Enigma的使用
发信人首先要调节三个转子的方向,而这个转子的初始方向就是密钥,是收发双方必须预先约定好的,然后依次键入明文,并把显示器上灯泡闪亮的字母依次记下来,最后把记录下的闪亮字母按照顺序用正常的电报方式发送出去。
收信方收到电文后,只要也使用一台恩尼格玛,按照原来的约定,把转子的方向调整到和发信方相同的初始方向上,然后依次键入收到的密文,显示器上自动闪亮的字母就是明文了。
加密的关键在于转子的初始方向。如果敌人收到了完整的密文,还是可以通过不断试验转动转子方向来找到这个密匙,特别是如果破译者同时使用许多台机器同时进行这项工作,那么所需要的时间就会大大缩短。对付这样暴力破译法(即一个一个尝试所有可能性的方法),可以通过增加转子的数量来对付,因为只要每增加一个转子,就能使试验的数量乘上26倍!
由于增加转子就会增加机器的体积和成本,恩尼格玛密码机的三个转子是可以拆卸下来并互相交换位置,这样一来初始方向的可能性一下就增加了六倍。假设三个转子的编号为1、2、3,那么它们可以被放成123-132-213-231-312-321这六种不同位置。
恩尼格玛还有一道保障安全的关卡,在键盘和第一个转子之间有块连接板。通过这块连接板可以用一根连线把某个字母和另一个字母连接起来,这样这个字母的信号在进入转子之前就会转变为另一个字母的信号。这种连线最多可以有六根,后期的恩尼格玛甚至达到十根连线,这样就可以使6对字母的信号两两互换,其他没有插上连线的字母则保持不变。当然连接板上的连线状况也是收发双方预先约定好的。
转子的初始方向、转子之间的相互位置以及连接板的连线状况组成了恩尼格玛三道牢不可破的保密防线,其中连接板是一个简单替换密码系统,而不停转动的转子,虽然数量不多,但却使整个系统变成了复式替换系统。
Enigma的破解
“暴力破译法”还原明文,需要试验多少种可能性:
三个转子不同的方向组成了26x26x26=17576种可能性;
三个转子间不同的相对位置为6种可能性;
连接板上两两交换6对字母的可能性则是异常庞大,有100391791500种;
于是一共有17576x6x100391791500,其结果大约为10,000,000,000,000,000!即一亿亿种可能性!

