矩阵及其运算
矩阵概念
定义:由个数
构成的
行
列的数表
称为维(型)是的矩阵(“matrix”),简称为
矩阵.
记为 或
,其中
为矩阵的第
行第
列元素.
i称为行标称为列标
**注:矩阵一般用大写字母A、B,… …表示_**
方阵
由n_2个数排成的_n×n矩阵
称为n阶方阵.记作A=(aij), i,j=1,2,…,n或
单位矩阵
如果n阶对角矩阵所有主对角线元素都是1,则称此矩阵为n阶单位矩阵.
单位矩阵在方阵运算中,起到类似数字“1”的作用.
对角矩阵
所有非主对角线元素全等于零的n阶矩阵称为对角矩阵.
记作或
零矩阵称为m×n零矩阵.
n阶零阵在方阵运算中,起到数字“0”的作用.
**_三角形矩阵_**<br />**如果**_**n**_**阶矩阵主对角线下方的元素都等于零,则称此矩阵为上三角矩阵.**<br />**如果**_**n**_**阶矩阵主对角线上方的元素都等于零,则称此矩阵为下三角矩阵.**
A为n阶上三角矩阵;B为n阶下三角矩阵.
矩阵的线性运算
同型矩阵和相等矩阵
定义 设有两个m×n矩阵 则称是同型矩阵。
若 则称矩阵A和B相等. 记作
矩阵相等必须满足:行列对应相等且元素对应相等.
矩阵加法
定义 设有两个m×n矩阵
称为矩阵A与B的和. 记作
注:只有同型的两个矩阵才能进行加法运算.
矩阵减法
设称为A的负矩阵.
矩阵的减法为
矩阵加法运算律
A、B、C和零矩阵O是同型矩阵.
数乘矩阵
定义 数k与矩阵A的乘积记作kA或 A k,规定为
-
运算规律:
其中A、B为m╳n矩阵;k、h为数.
**_矩阵乘法_**<br />**定义 1 × s矩阵与s × 1矩阵的乘积是一个1阶方阵,也就是一个数.**<br />**即**
注意:只有当第一个矩阵的列数等于第二个矩阵的 行数时,两个矩阵才能相乘.
注:一般地,矩阵的乘法不满足交换律,即AB≠BA,而且两个非零矩阵的乘积可能是0矩阵
注:与数的乘法不同,两个非零矩阵的乘积可能是零阵,反过来,如果两个矩阵的乘积是零阵,不能断定A或B一定是零阵.
矩阵转置的性质(假设运算都是可行的)

方阵的幂
设A是一个n阶方阵,k为正整数,称为A的k次幂.
A k 就是k个A连乘.显然只有方阵的幂才有意义.规定:
运算律
其中为正整数.
①因为矩阵乘法一般不满足交换律,所以对于两个,n阶方阵A与B,一般不等于
.即
②如果Ak=O,不一定有A=O. 例如取
n 阶方阵行列式
(1)定义 由n阶矩阵A的元素构成的行列式,称为矩阵A的行列式.记作.
矩阵A: 行列式
:
注 矩阵与行列式是两个不同的概念,n阶矩阵是个数,按一定方式排成的数表,而n阶行列式则是这些数按一定的运算法则所确定的一个数.
**_方阵行列式的性质_**<br />**_A_、_B_为_n_阶矩阵,****为数**<br /> 
n阶矩阵A、B,一般AB不等于BA,但总有
线性变换的系数矩阵
n个变量x_1,x_2,⋯,x_n 与n个变量y_1,y_2,⋯,y_n 之间的关系式
表示一个从变量 到变量
的线性变换,其中
为常数.
系数 构成矩阵
称矩阵A为线性变换的系数矩阵.则
线性变换与矩阵A之间存在着一一对应关系
逆矩阵
定义 对于n阶方阵A,如果有一个n阶方阵B,使得 ,则方阵A称为可逆矩阵,
简称A可 逆. 方阵B称为A的逆矩阵.记为.
定理:如果方阵A可逆,则A的逆矩阵是惟一的.
证 设B、C都是A的逆矩阵,则有.惟一性得证.
**_伴随矩阵_**<br />**A是n阶方阵**
元素 的代数余子式
位于第 j 行第 i列
是
的伴随矩阵
矩阵的伴随矩阵是
伴随矩阵的性质
定理:
证明:
因此
**_矩阵可逆的判定定理_**<br />**定理:方阵_A_可逆的充分必要条件是****且**<br /><br />**(此时,称矩阵_A_为非奇异矩阵)**<br />**若方阵_A_可逆,则**** **<br />** 定理 对于_n _阶方阵_A_、_B_,如果 ****那么_A_、_B_都是可逆矩阵,并且它们互为逆矩阵.**
逆矩阵性质
如果 n 阶方阵A、B可逆,那么与
也可逆,且
求逆矩阵
**_性线变换的逆变换_**
线性变换的系数矩阵是一个n 阶方阵 A,若记
则上述线性变换可记作
若可逆,则

矩阵方程
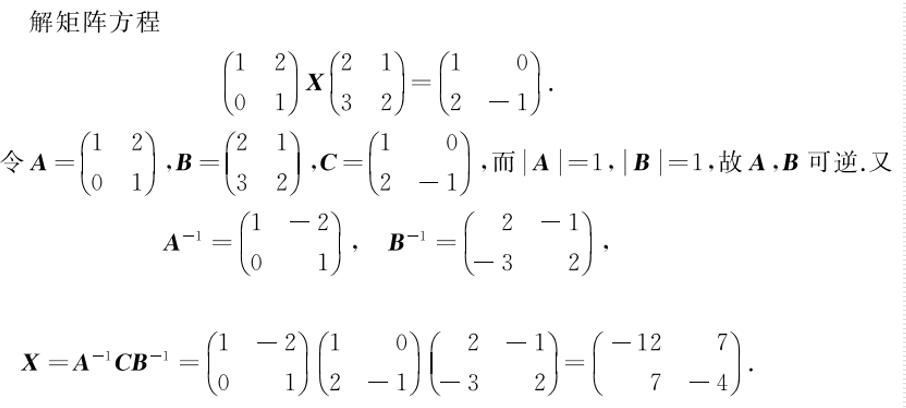
矩阵多项式与分块矩阵
矩阵多项式
定义 设为x 的多项式,A为n 阶矩阵,E为n阶单位阵,称
为关于A的矩阵多项式.
**_分块矩阵_**<br />**一、分块矩阵的概念**<br />**矩阵的分块就是将矩阵A用若干纵线和横线分成几个小矩阵,每一小矩阵称为A的子块,以子块为元素的形式上的矩阵,称为分块矩阵。**<br />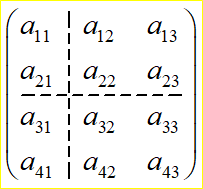
**_按行分块以及按列分块_**<br />**矩阵 **_**A **_**有**_** **_**行****列,若将第 ****行记作**<br />**若将第****列记作****则**
**_分块矩阵的运算_**<br />**1.分块矩阵相加、减**<br />**设A、B是两个用相同方法分块的同型矩阵**<br />(**1)分块矩阵的和、差:**<br />**且****,及对应的子块****与****有相同的行数和相同的列数;则**
2.数与分块矩阵相乘
设是一个实数,
3.分块矩阵相乘
设 A 为 矩阵,B 为
矩阵,若把 A 按行分块,把 B 按列块,则
特别地,分块对角阵乘法:其中Ai、Bi是同阶子方阵,则
**_分块矩阵的转置_**
若,则
分块矩阵不仅形式上进行转置,而且每一个子块也进行转置.
**_分块对角矩阵的性质_**
1.
2.
克莱姆法则
如果线性方程组(1)
简记为: 的系数行列式不等于零,即
那么线性方程组(1)有解并且解是唯一的,解可以表示成
其中是把系数行列式
中第
列的元素用方程组右端的常数项代替后,所得到的
阶行列式,即
证:由,而
,因此
可逆,从而
定理5也称为克莱姆法则,它是求解线性方程组的一种方法,但是具有一定的局限性
定理中包含着三个结论:
•方程组有解;(解的存在性)
•解是唯一的;(解的唯一性)
•解可以由公式(2)给出.
这三个结论是有联系的. 应该注意,该定理所讨论的只是系数行列式不为零的方程组,至于系数行列式等于零的情形,将在第三章的一般情形中一并讨论.
关于克莱姆法则的等价命题
设(1)
定理4 如果线性方程组(1)的系数行列式不等于零,则该线性方程组一定有解,而且解是唯一的 .
定理4′如果线性方程组无解或有解但解不唯一,则它的系数行列式必为零.
齐次线性方程组
线性方程组
常数项全为零的线性方程组称为齐次线性方程组,否则称为非齐次线性方程组.
齐次线性方程组总是有解的,因为(0,0,…, 0)就是一个解,称为零解. 因此,齐次线性方程组一定有零解,但不一定有非零解.
我们关心的问题是,齐次线性方程组除零解以外是否存在着非零解.
**_齐次线性方程组的相关定理_**<br />**定理5如果齐次线性方程组的系数行列式****则齐次线性方程组只有零解,没有非零解.**<br />**定理5′如果齐次线性方程组有非零解,则它的系数行列式必为零. **<br />**备注**<br />1.**这两个结论说明系数行列式等于零是齐次线性方程组有非零解的必要条件. **<br />2.**在第三章还将证明这个条件也是充分的. 即:**<br />**齐次线性方程组有非零解****系数行列式等于零**
思考题
当线性方程组的系数行列式为零时,能否用克拉默法则解方程组?为什么?此时方程组的解为何?
当线性方程组的系数行列式为零时,不能用克拉默法,则解方程组,因为此时方程组的解为无解或有无穷多解.

