内容概要:数据在计算机中的存储和运算、相关习题
数据的表示方法
r 进制数:基数 r,每个数码位可能出现 r 种字符,逢 r 进 1
r 进制数⟶十进制:各数码位与位权的乘积之和
十进制⟶r 进制:
- 整数部分:除基取余法,先取得的 “余” 是整数的低位
- 小数部分:乘基取整法,先取得的 “整” 是小数的高位
二进制⟶八进制:每 3 个二进制对应一个八进制位
二进制⟶十六进制:每 4 个二进制位对应一个十六进制位
注意 “补位”
真值和机器数
- 真值:现实中带正负号的数值
- 机器数:把正负号数字化的数
ASCII 码:通常用 8bit 表示一个字符,最高位都为 0。共 128 个字符,0-31、127 为控制 / 通信字符;32-126 为可印刷字符。所有大写字母、所有小写字母、所有数字的编码都连续。
汉字:区位码 94×94。国标码 = 区位码 + 2020H。机内码 = 国标码 + 8080H。
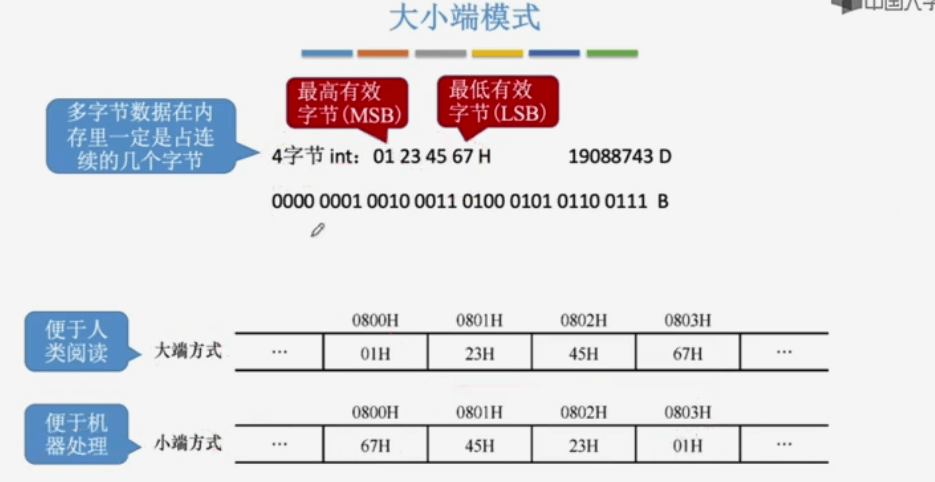
字符串:从低地址到高地址逐个字符存储,常采用‘\0’作为结尾标志。对于多字节的数据 (如汉字),可采取大 / 小端存储模式。大端模式:将数据的最高有效字节存放在低地址单元中。小端模式:将数据的最高有效字节存放在高地址单元中。
组成奇偶校验码的基本方法:在 n 位有效信息位上增加一个二进制校验位,构成一个 n+1 位奇偶校验码。
奇校验:使 n+1 位的奇偶校验码中 1 的个数为奇数。 偶校验:使 n+1 位的奇偶校验码中 1 的个数为偶数。
定点数的表示
定点数:小数点的位置固定
Eg:996.007 ——常规计数
浮点数:小数点的位置不固定
Eg:9.96007×102 ——科学计数法
无符号数:整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值。
通常只有无符号整数,而没有无符号小数
真值 0 有 + 0 和 - 0 两种形式
反码:正数的反码 = 原码,负数的反码 = 数值位取反
补码:正数的补码 = 原码,负数的补码 = 反码末位 + 1(要考虑进位)。将负数补码转回原码的方法相同:尾数取反,末位 + 1。
技巧:由 [x] 补 快速求 [-x] 补 的方法 符号位、数值位全部取反,末位 + 1
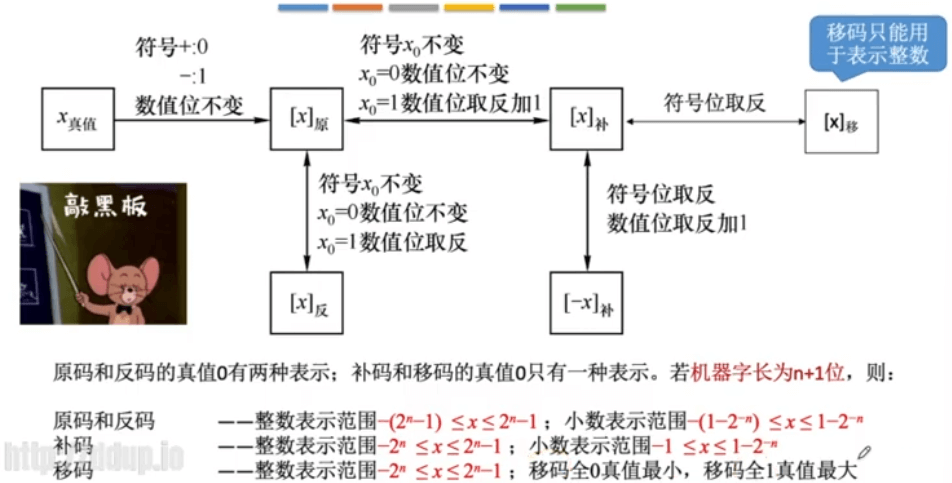
移码:补码的基础上将符号位取反。移码 = 真值 + 偏置值
注意: 移码只能用于表示整数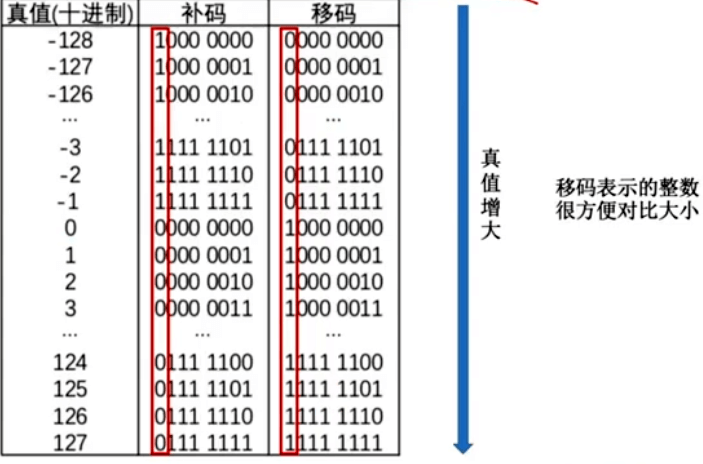
原码和反码的真值 0 有两种表示;补码和移码的真值 0 只有一种表示形式。
定点数移位运算
算术移位
- 左移 1 位相当于 × 基数;右移 1 位相当于 ÷ 基数
- 原码、反码:符号位不参与移位。左移、右移都补 0
- 补码:符号位不参与移位。左移补 0、右移补符号数负数补码最右边的 1 及其右边与原码相同,最右边的 1 的左边与反码相同
逻辑移位
- 左移右移都补 0,移出的位舍弃
循环移位
- 不带进位位:用移出的位补上空缺
- 带进位位:移出的位放到进位位,原进位位补上空缺
定点数加减运算和溢出判断
定点数加减运算一律用补码
补码减法
- 将减数 x 取负得 [-x] 补,转变为加法 [A-B] 补 =[A] 补 +[-B] 补,符号位参与运算
溢出判断(补码)
- 上溢:正数 + 正数 = 负数
- 下溢:负数 + 负数 = 正数
- 采用双符号位,正数符号为 00,负数符号为 11。运算后若双符号位 = 01,则发生上溢;若双符号位 = 10,则发生下溢;若两个符号位相同则未发生溢出
- 双符号位补码相加的结果, 不论溢出与否, 最高符号位始终指示正确的符号
定点数乘法运算
原码乘法
运算器实现原码一位乘法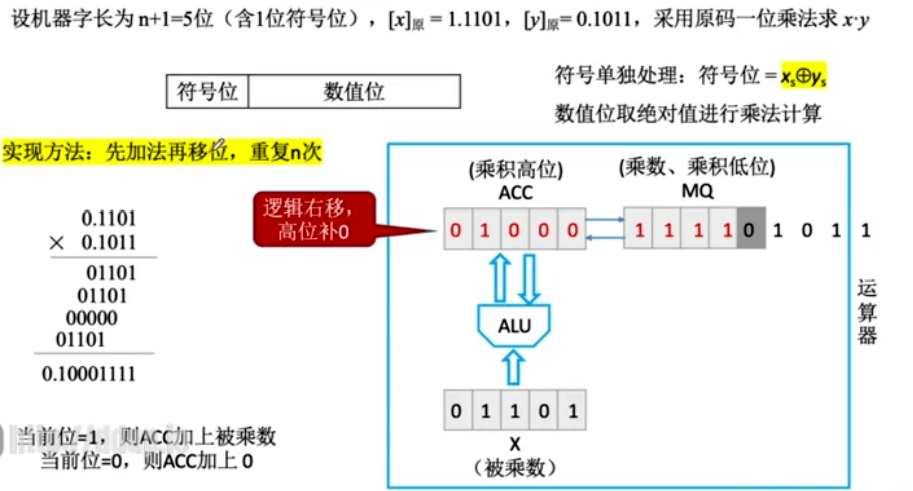
符号位通过异或确定;数值部分通过被乘数和乘数绝对值的 n 轮加法、移位完成。根据当前乘数中参与运算的位(MQ 最低位)确定 (ACC) 加什么。若当前运算位 =1,则(ACC)+[|x|] 原;若 =0,则 (ACC)+0。
手算模拟运算器实现原码一位乘法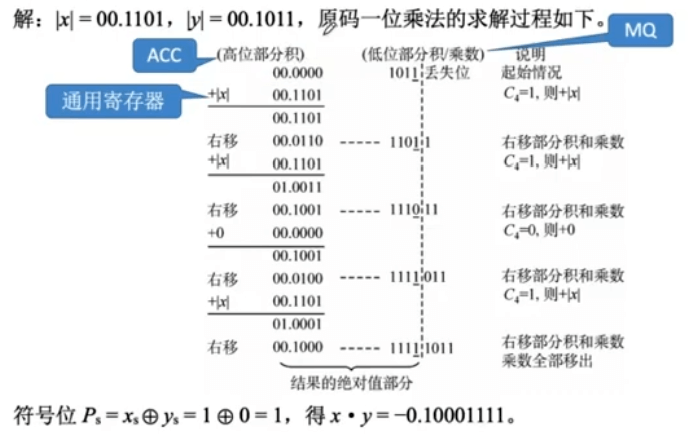
补码乘法
运算器实现补码一位乘法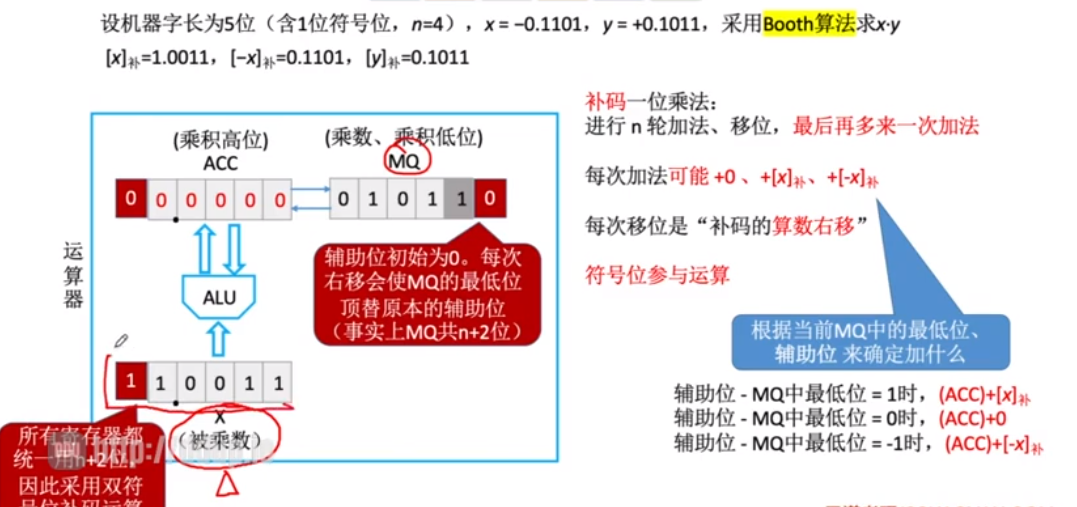
手算模拟运算器实现补码一位乘法
原码一位乘法与补码一位乘法对比⭐
定点数除法运算
原码除法
恢复余数法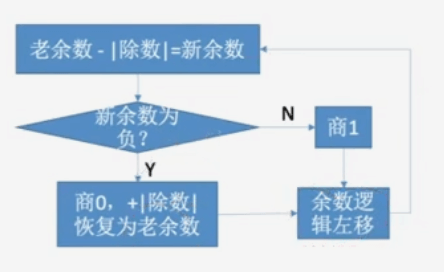
加减交替法(不恢复余数法)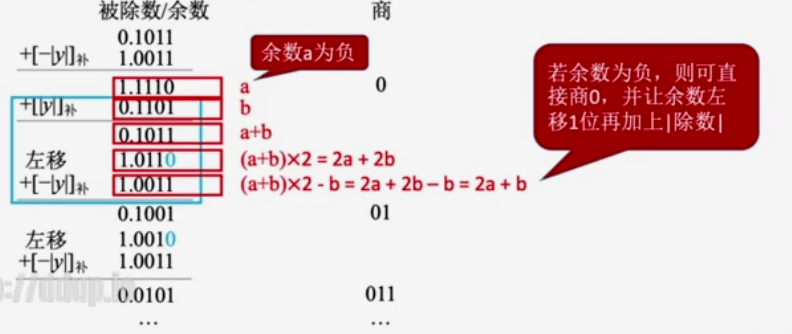
恢复余数法:减除数,若余数为负数,商 0,加除数**,逻辑左移,减除数,得新余数;若余数为正数,商 1,逻辑左移,减除数,得新余数⭐
不恢复余数法:减除数,若余数为负数,商 0,逻辑左移,加除数**,得新余数;若余数为正数,商1,逻辑左移,减除数,得新余数⭐补码除法
加减交替法
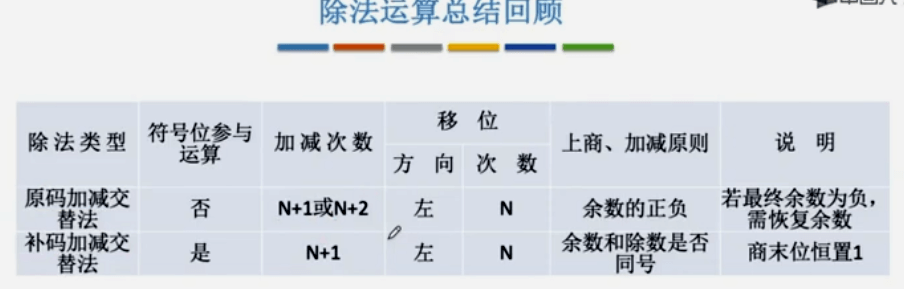
强制类型转换
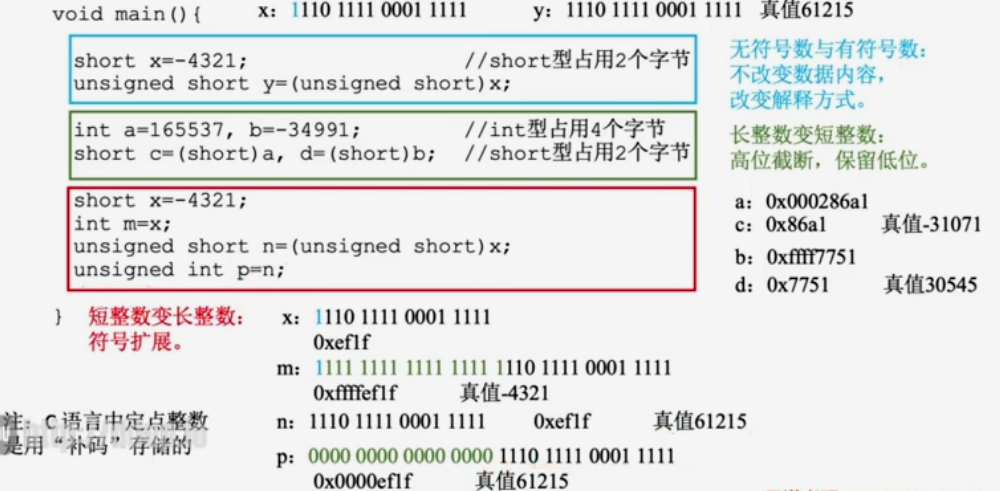
补码位扩展
边界对齐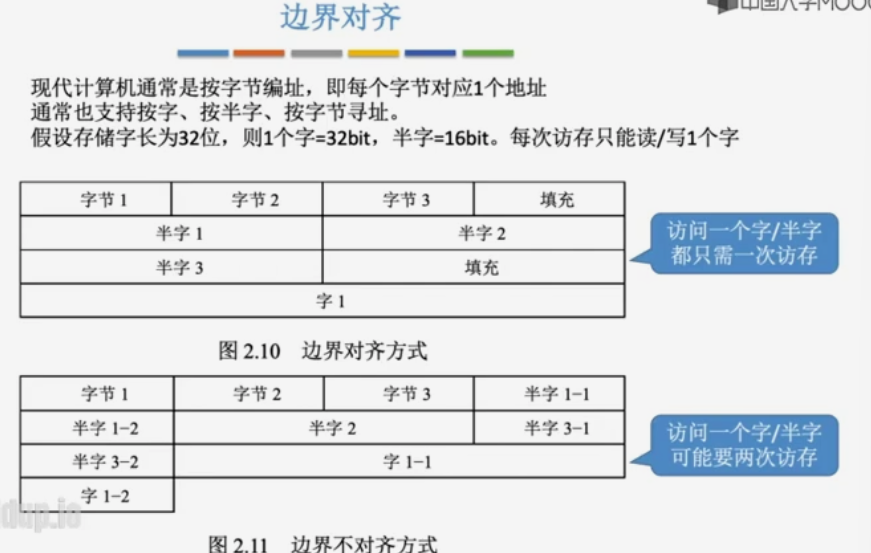
浮点数的表示
表示
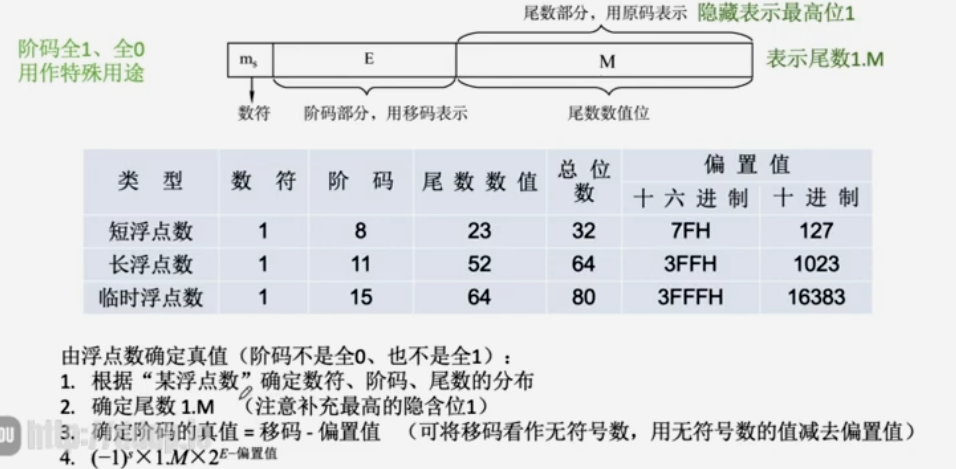
阶码 + 尾数
- 尾数给出具体数值,阶码指明小数点前移、后移多少位
- 阶码通常是用补码、移码表示的定点整数
- 尾数通常是用补码、原码表示的定点小数
规格化
- 尾数的最高数值位必须是一个有效值(类比十进制科学计数法,通常我们会让数值部分最高位为非 0)
- 左规:数值位最高位无效时,通过尾数算术左移、阶码减 1 的方法处理,直到尾数最高数值位有效时停止
- 右规:若采用双符号位表示尾数,则当运算后尾数 “假溢出” 时,可以通过尾数右移、阶码加 1 的方法处理
- 原码表示的尾数规格化:尾数的最高数值位必须是 1
- 补码表示的尾数规格化:尾数最高数值位必须和尾数符号位相反
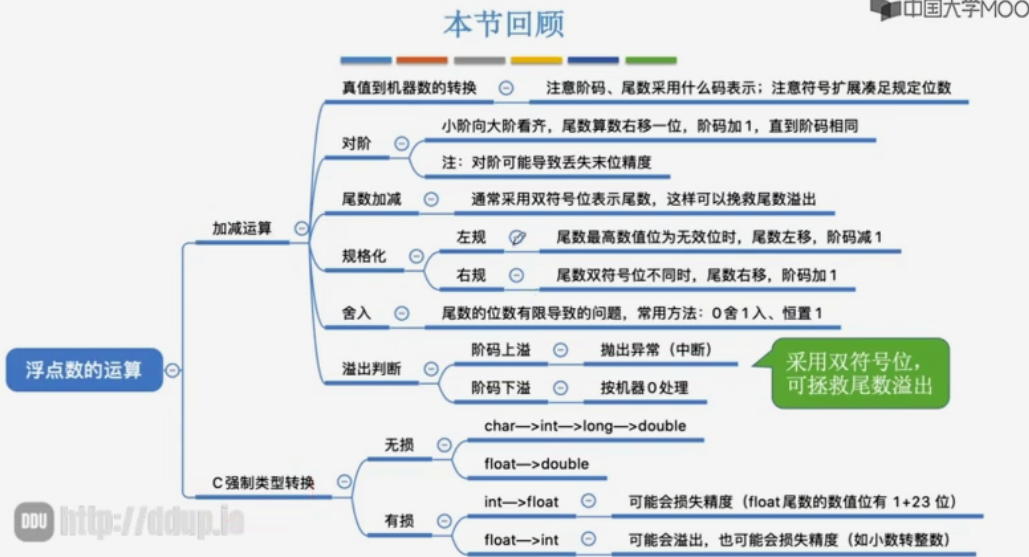
浮点数的运算
习题
- 已知 [X] 原,求 [X/2] 原和 [2X] 原 。
①[X] 原 = 0.0110000 ; ②[X] 原 =10011010
解析:
原码算术移位:符号位不变,数值部分左移或右移,移出的空位填 “0”。(左移一位相当于乘以 2,右移一位相当于除以 2)
① [X/2] 原=0.0011000 [2X] 原=0.1100000
② [X/2] 原= 10001101 [2X] 原= 10110100
- 设机器字长为 8 位,写出 + 0.375 和-0.6875 的二进制原码表示。
解析::先转二进制再加符号位得原码
(+0.375)10 = (+0.011)2 [+0.011] 原=0.011 = 0.0110000
(-0.6875)10 = (-0.1011)2 [-0.1011] 原=1.1011 = 1.1011000
- 已知 x,求 x 的补码 [x] 补。
①x=+0.1010110 ②x=-0.1010110 ③x=+1010110 ④x=-1010110
解析::先加符号位转成原码,然后转补码,正数不变,负数数值位取反加 1
①[x] 补 =0.1010110 ② [x] 补 =1.0101010 ③ [x] 补 =01010110 ④ [x] 补=10101010
- 已知 [x] 补,求 [2x] 补、[x/2] 补
(1) [x] 补=0.0101001, (2)[x] 补=11011010
解析:
补码算术移位:符号位不参与移位。左移补 0、右移补符号位
(1) [2x] 补 =0.1010010 [x/2] 补 = 0.0010100
(2) [2x] 补 =10110100 [x/2] 补 =11101101
- 已知 [x] 补,求 [-x] 补
(1) [x] 补=1.0011010 ,(2) [x] 补=10110010
解析::各位 (含符号位) 取反取反加 1
(1) [-x] 补=0.1100110
(2) [-x] 补=01001110
- 将下列 x 的原码表示转化为补码表示。
[x] 原=0.1010110 [x] 原=1.1010110 [x] 原=01010110 [x] 原=11010110
解析::正数不变,负数数值位取反加 1
[x] 补 =0.1010110 [x] 补 =1.0101010 [x] 补 =01010110 [x] 补 =10101010
- 一个 C 语言程序在一台 32 位机器上运行。程序中定义了三个变量 x、y、z,其中 x 和 z 是 int 型,y 为 short 型。 当 x=127,y=-9 时,执行赋值语句 z=x+y 后,x、y 和 z 的机器码分别是()
A.X=0000007FH,y=FFF9H,z=00000076H
B.X=0000007FH,y=FFF9H,z=FFFF0076H
C.X=0000007FH,y=FFF7H,z=FFFF0076H
D.X=0000007FH,y=FFF7H,z=00000076H
解析:
在 C 语言中,数据用补码存储。int 型占 4 字节,32 位;short 型占 2 字节,16 位。定点整数补码的位扩展是前面补符号数
[x] 补 =01111111=0000,0000,0000,0000,0000,0000,0111,1111=0000007FH
[y] 补 =10111=1111,1111,1111,0111=FFF7H
[z] 补 =[x+y] 补 =[x] 补 +[y] 补 =01111111+11110111=01110110=0000,0000,0000,0000,0000,0000,0111,0110 =00000076H
也可以直接 127+(-9)=118=01110110=0000,0000,0000,0000,0000,0000,0111,0110 =00000076H
所以答案为 D
8. 假定编译器规定,int 型占 32 位,short 型占 16 位, 若有下列 C 语言语句:
unsigned short x=65530;
unsigned int y=x;
得到 y 的机器数为()
A. 0000 7FFAH
B. 0000 FFFAH
C. FFFF 7FFAH
D. FFFF FFFAH
解析:
在 C 语言中,数据用补码存储。无符号数与有符号数之间转换:不改变数据内容,改变解释方式。短整数\longrightarrow⟶长整数:位扩展。无符号整数位扩展在前面补 0。
216=65536, 所以 16 个 1 为 65535
short [x] 补 =11111111,11111010
int [y] 补 =00000000,00000000,11111111,11111010=0000FFFAH
所以答案为 B
9. 假定有 4 个整数用 8 位补码分别表示 r1=FEH, r2=F2H,r3=90H,r4=F8H,若将运算结果存放在一个 8 位寄存器中,则下列运算会发生溢出的是 ()
A. r1×r2
B. r2×r3
C. r1×r4
D. r2×r4
解析:
用补码表示时 8 位寄存器所能表示的整数范围为 - 128 到 + 127
r1=FEH=1111,1110 r1 补 =1000,0010=-2
r2=F2H=1111,0010 r2 补 =1000,1110=-14
r3=90H=1001,0000 r3 补 =1111,0000=-112
r4=F8H=1111,1000 r4 补 =1000,1000=-8
则 r1×r2=28,r2×r3=1568,r1×r4=16,r2×r4=112,只有 r2×r3 结果溢出
所以答案为 B
10. 在 32 位计算机上,考虑以下 C 语言代码:
short si=-8196;
int i=si;
执行上述程序段后,i 的机器数表示为 ()
A. 0000 9FFCH
B. 0000 DFFCH
C. FFFF 9FFCH
D. FFFF DFFCH
解析:
在 C 语言中,数据用补码存储。int 型占 4 字节,32 位;short 型占 2 字节,16 位。短整数\longrightarrow⟶长整数:位扩展。定点整数补码的位扩展是前面补符号数 213=8192, 所以第 14 位为 1 是 8192
short [si] 原 = 110,0000,0000,0100
short [si] 补 = 101,1111,1111,1100=1101,1111,1111,1100
int[i] 补 =1111,1111,1111,1111,1101,1111,1111,1100=FFFF DFFCH
所以答案为 D
11. 某机器字长 8 位,采用补码形式(其中 1 位为符号位),则机器数能表示的范围是__。
A. -127~127
B. -128~128
C. -128~127
D. -127~128
解析:
最大正数:0111,1111 = 127。正数原码 = 补码
最小负数:1000,0000 = -128。符号位同时也可以看做数字位即表示 - 128,转换成补码为 1,0000,0000
验证:127(0111,1111)+1(0000,0001)=-128(1000 0000)
8 位二进制的补码取值范围是 - 128-127
所以答案为 C
12.8 位补码定点整数 1001 0101 扩展成 16 位后的值用 16 进制表示为
A.0095H
B.9500H
C.FF95H
D.95FFH
解析:
考查补码定点整数位扩展:前面补符号数
1111,1111,1001,0101 = FF95H
所以答案为 C
13. 考虑以下 C 语言代码:
short si=-8196;
unsigned short usi=si;
执行上述程序段后,usi 的值为多少()
A.8196
B.34572
C.57339
D.57340
解析:
在 C 语言中,数据用补码存储。short 型占 2 字节,16 位。无符号数与有符号数之间转换:不改变数据内容,改变解释方式。
213=8192,所以第 14 位为 1 代表 8192,即
short [si] 原 =110,0000,0000,0100
short [si] 补 =101,1111,1111,1100=1101,1111,1111,1100
unsigned short [usi] 补 =1101,1111,1111,1100
216=65536, 所以 16 个 1 为 65535,又 213=8192, 可得
[usi] 补 =65535-8192-2-1=57340
所以答案为 D
14.(统考 2015-13) 由 3 个 “1” 和 5 个 “0” 组成的 8 位二进制补码, 能表示的最小整数是()
A.-126
B.-125
C.-32
D.-3
解析:
-128=1000,0000,转换成补码为 1,0000,0000
-127=1111,1111,转换成补码为 1000,0001
-126=1111,1110,转换成补码为 1000,0010
……
由以上分析可得:只要 3 个 “1” 和 5 个 “0” 组成的补码最小,则转换成原码再转换成的十进制整数也最小,
补码:1000,0011,原码:1111,1101,转换成十进制即 - 125
所以答案为 B
15.(统考 2019-13) 考虑以下 C 语言代码:
unsigned short usi=65535;
short si=usi;
执行上述程序段后,si 的值为多少()
A.-1
B.-32767
C.-32768
D.-65535
解析:
在 C 语言中,数据用补码存储。short 型占 2 字节,16 位。无符号数与有符号数之间转换:不改变数据内容,改变解释方式。
216=65536
unsigned short [usi] 补 =1111,1111,1111,1111
short [si] 补 =1111,1111,1111,1111=-32767
[si] 原 =1000,0000,0000,0001=-1
所以答案为 A
16. 将十进制真值 (-127,-1,0,+1,+127) 列表表示成二进制数及原码、反码、补码、移码值
解析:
| 二进制数 | 原码 | 反码 | 补码 | 移码 | |
|---|---|---|---|---|---|
| -127 | -0111,1111 | 1111,1111 | 1000,0000 | 1000,0001 | 0000,0001 |
| -1 | -0000,0001 | 1000,0001 | 1111,1110 | 1111,1111 | 0111,1111 |
| 0000,0000 | 0000,0000 | 0000,0000 | 1000,0000 | ||
| 0 | 0000,0000 | ||||
| 1000,0000 | 1111,1111 | 0000,0000 | 1000,0000 | ||
| +1 | +0000,0001 | 0000,0001 | 0000,0001 | 0000,0001 | 1000,0001 |
| +127 | +0111,1111 | 0111,1111 | 0111,1111 | 0111,1111 | 1111,1111 |
0 在 [x] 原和 [x] 反中有两种表示
17. 已知x1 =-0.1110,x2=+0.1101,
求:[x1] 补,[-x1] 补, [x2] 补,[-x2] 补。
解析:
[x] 补\longleftrightarrow⟷[-x] 补:各位 (含符号位) 取反取反加 1
[x1] 补=1.0010
[-x1] 补=0.1110
[x2] 补=0.1101
[-x2] 补=1.0011
18.x=+0.1101,y=+0.0110, 求x-y
解析:
[x] 补 =0.1101
[y] 补 =0.0110
[-y] 补 =1.1010
[x-y] 补 =[x] 补 +[-y] 补 =0.1101+1.1010=0.0111
所以 x-y=+0.0111
算术运算验证:0.1101-0.0110=+0.0111
19.(1)x=+0.1100, y=+0.1000, 求x+y
(2)x=-0.1100, y=-0.1000, 求x+y
解析:
运算后若双符号位 = 01,则发生上溢;若双符号位 = 10,则发生下溢。双符号位补码相加的结果, 不论溢出与否, 最高符号位始终指示正确的符号。
(1)[x+y] 补 =00.1100+00.1000=01.0100
双符号位出现 “01”, 表示上溢, 即结果大于+1
(2)[x+y] 补 =11.0100+11.1000=10,1100
双符号位出现 “10”, 表示下溢, 即结果小于-1。
20. 某字长 8 位的计算机中,已知整型变量 x、y 的机器数分别为 [x] 补 =11110100,[y] 补 =10110000。若整型变量 z=2×x+y/2,则 z 的机器数为( )
A. 11000000
B. 00100100
C. 10101010
D. 溢出
解析:
补码:符号位不参与移位。左移补 0、右移补符号位
[2X] 补 =11101000
[y/2] 补 =11011000
[Z] 补 =[2X] 补 +[y/2] 补 =11101000+11011000=11000000
所以答案为 A
21. 若浮点数 x 的 IEEE754 标准存储格式为 (41360000)16,求其浮点数的十进制数值。
解析:
由浮点数确定真值:
- 确定数符 S、阶码 E、尾数 M 的分布
- (-1)s×1.M×2E-127
IEEE754 32 位标准:1+8+23
(41360000)16=(0100,0001,0011,0110,0000,0000,0000,0000)2
数符 s=0,阶码 E=(1000,0010)2=(130)10,尾数 M=011011
X=(-1)s×1.M×2E-127=(-1)0×1.0111011×2130-127=+(1.011011)×23=+1011.011=(11.375)10
22. 将 (20.59375)10 转换成 IEEE754 标准的 32 位浮点数的二进制存储格式。
解析:
由真值确定浮点数:
- 转换为二进制,移动小数点
- 确定数符 S、阶码 E、尾数 M 的分布
(20.59375)10=(10100.10011)2=(1.010010011)2×24
S=0,E=4+127=131=1000,0011,M=010010011
最后得到 32 位浮点数的二进制存储格式为:
0100,0001,1010,0100,1100,0000,0000,0000=(41A4C000)16
23. 将 5/32 及 - 4120 表示成 IEEE754 单精度浮点数格式,并用十六进制书写
解析:
由真值确定浮点数:
- 转换为二进制,移动小数点
- 确定数符 S、阶码 E、尾数 M 的分布
(1) (5/32)=(0.00101)2=(1.01)×2-3
S=0,E=-3+127=124=0111,1100,M=01
0011,1110,0010,0000,0000,0000,0000,0000=(3E200000)16
(2) (-4120)=(1000,0000,1100,0)=(1.000000011000)×212
S=1,E=12+127=139=10001011,M=000000011
1100,0101,1000,0000,1100,0000,0000,0000=C580C000H
24. 将十六进制的 IEEE754 单精度浮点数 42E48000 转换成十进制数。
解析:
由浮点数确定真值:
- 确定数符 S、阶码 E、尾数 M 的分布
- (-1)s×1.M×2E-127
42E48000=0100,0010,1110,0100,1000,0000,0000,0000
S=0,E=1000,0101=133,M=1100,1001
(-1)0×(1.11001001)×26=1110010.01=114.25
25. 设机器字长 16 位, 定点表示, 尾数 15 位, 数符 1 位, 问:
(1) 定点原码整数表示时, 最大正数是多少? 最小负数是多少?
(2) 定点原码小数表示时, 最大正数是多少? 最小负数是多少?
解析:
(1) 定点原码整数
最大正数:0111,1111,1111,1111=215-1=32767
最小负数:1111,1111,1111,1111=-(215-1)=-32767
(2) 定点原码小数
最大正数:+0.111,1111,1111,1111,=1-2-15
最小负数:-0.111,1111,1111,1111,=-(1-2-15)
26. 假设由 S,E,M 三个域组成的一个 32 位二进制字所表示的非规格化浮点数x, 真值表示为:
X=(-1)s×1.M×2E-128
其中数符 S 为 1 位,阶码 E 为 8 位,尾数 M 为 23 位。
请问:x 所表示的最大正数、最小正数、最大负数、最小负数是多少?
解析:
最大正数:0111,1111,1111,1111,1111,1111,1111,1111
最小正数:0000,0000,0000,0000,0000,0000,0000,0000
最大负数:1000,0000,0000,0000,0000,0000,0000,0000
最小负数:1111,1111,1111,1111,1111,1111,1111,1111
27.float 类型(即 IEEE754 单精度浮点数格式)能表示的最大正整数是()
A. 2126-2103
B. 2127-2104
C. 2127-2103
D. 2128-2104
解析:
0111,1111,0111,1111,1111,1111,1111,1111
E=254,e=254-127=127,M=111,1111,1111,1111,1111,1111=(1-2-23)10
(-1)0×(1.111……)×2127=[1+(1-2-23)]×2127=(2-2-23)×2127=2128-2104
所以答案为 D
28. 假定变量 i,f,d 数据类型分别为 int, float, double(int 用补码表示,float 和 double 用 IEEE754 单精度和双精度浮点数据格式表示),已知 i=785,f=1.5678e3,d=1.5e100, 若在 32 位机器中执行下列关系表达式,则结果为真的是() (I) i==(int)(float)i
(II) f==(float)(int)f
(III) f==(float)(double)f
(IV) (d+f)-d==f
A. 仅 I 和 II
B. 仅 I 和 III
C. 仅 II 和 III
D. 仅 III 和 IV
解析:
由于 (int)f=1,所以 II 错。IV 的计算过程是先将 f 转换成双精度,然后加法运算,故得到 (d+f)-d 双精度,而 f 为单精度,所以 IV 错
所以答案为 B
29.float 型数据通常用 IEEE 754 单精度浮点数格式表示。若编译器将 float 型变量 x 分配在一个 32 位浮点寄存器 FR1 中,且 x = -8.25,则 FR1 的内容是()
A. C104 0000H
B. C242 0000H
C. C184 0000H
D. C1C2 0000H
解析:
由真值确定浮点数:
- 转换为二进制,移动小数点
- 确定数符 S、阶码 E、尾数 M 的分布
(-8.25)10=(1000.01)2=(1.00001×23)
S=1,E=3+127=130=1000,0010,M=00001
1100,0001,0000,0100,0000,0000,0000,000=C104 0000H
所以答案为 A
30. 某数采用 IEEE 单精度浮点数格式表示为 C640 0000H, 则该数的值是 ( )
A. -1.5×213
B. -1.5×212
C. -0.5×213
D. -0.5×212
解析:
由浮点数确定真值:
- 确定数符 S、阶码 E、尾数 M 的分布
- (-1)s×1.M×2E-127
C640 0000=1100,0110,0100,0000,0000,0000,0000,0000
S=1,E=1000,1100=140,e=E-127=13,M=1
(-1)1×(1.1)×213=-1.5×213
所以答案为 A
31. 设x=2010×0.11011011,y=2100×(-0.10101100), 求 x+y。
解析:
浮点加减运算操作:
- 求阶差并对阶 (小阶向大阶)
- 尾数进行加或减运算
- 结果规格化
- 舍入处理
- 判溢出
注:
- 两数均以补码表示, 阶码采用双符号位, 尾数采用单符号位
- 补码算术右移:补符号数;补码算术左移:补 0
- 补码表示的尾数规格化:尾数最高数值位必须和尾数符号位相反
x:[Ex] 补 =00010,[Mx] 补 =0.11011011
y:[Ey] 补 =00100,[My] 补 =1.01010100
求阶差:△E = Ey - Ex = [ Ey ] 补 + [ - Ex ] 补 = 00100 + 11110 = 00010=+2
对阶后:[Ex] 补 =00100,[Mx] 补 =0.00110110(11),其中 (11) 表示[Mx] 补右移 2 位后移出的最低两位数
尾数加:[Mx] 补 + [My] 补 = 0.00110110(11) + 1.01010100 = 1.10001010(11)
规格化:左规 1.10001010(11) = 1.00010101(10),E=00011
0 舍 1 入:1.00010101 + 0.00000001 = 1.00010110
判溢出:阶码符号位为 00, 不溢出, 故得最终结果为
x+y=2011×(-0.11101010)
32. 在浮点数原码运算时, 判定结果为规格化数的条件是 。
A. 阶的符号位与尾数的符号位不同
B. 尾数的符号位与最高数值位相同
C. 尾数的符号位与最高数值位不同
D. 尾数的最高数值位为 1
解析:
原码表示的尾数规格化:尾数的最高数值位必须是 1
所以答案为 D
33. 若浮点数用补码表示,则判断运算结果是否为规格化数的方法是
A. 阶符与数符相同为规格化数
B. 阶符与数符相异为规格化数
C. 数符与尾数小数点后第一位数字相异为规格化数
D. 数符与尾数小数点后第一位数字相同为规格化数
解析:
补码表示的尾数规格化:尾数最高数值位必须和尾数符号位相反
所以答案为 C
34. 浮点数加减运算过程一般包括对阶、尾数运算、规格化、舍入和判溢出等步骤。设浮点数的阶码和尾数均采用补码表示,且位数分别为 5 位和 7 位(均含 2 位符号位)。若有两个数 X=27×29/32,Y=25×5/8,则用浮点加法计算 X+Y 的最终结果是()
A. 00111 1100010
B. 00111 0100010
C. 01000 0010001
D. 发生溢出
解析:
浮点加减运算操作:
- 求阶差并对阶 (小阶向大阶)
- 尾数进行加或减运算
- 结果规格化
- 舍入处理
- 判溢出
[Ex] 补 =00111,[Mx] 补 =00.11101
[Ey] 补 =00101,[My] 补 =00.10100
阶差 = 2,y 向 x 看齐,[E] 补 =00111,[My] 补 =00.00101(00)
[Mx] 补 + [My] 补 = 00.11101 + 00.00101(00) = 01.00010
发生尾数上溢,但是阶码 00111,已经达到最大,尾数无法移位调整,发生无法拯救的尾数上溢
所以答案为 D
选择题中简便方法:
在十进制中,X=27×29/32,Y=25×5/8=27×5/32
X+Y=27×(29/32+5/32),尾数大于 1,发生尾数上溢,阶码数值位只有 3 位,最大为 7,尾数无法移位调整,发生无法拯救的尾数上溢
所以答案为 D
35. 下列有关浮点数加减运算的叙述中,正确的是 ( )
Ⅰ. 对阶操作不会引起阶码的上溢或下溢
Ⅱ. 右规和尾数舍入都可能引起阶码的上溢
Ⅲ. 左规时可能引起阶码的下溢
Ⅳ. 尾数溢出时结果不一定溢出
A. 仅 Ⅱ、Ⅲ
B. 仅 Ⅰ、Ⅱ、Ⅳ
C. 仅 Ⅰ、Ⅲ、Ⅳ
D. Ⅰ、Ⅱ、Ⅲ、Ⅳ
解析:
对阶是较小的阶码对齐至较大的阶码,Ⅰ 正确。
右规和尾数舍入过程,阶码加 1 而可能上溢,Ⅱ 正确,
同理 Ⅲ 也正确。
尾数溢出时可能仅产生误差,结果不一定溢出,Ⅳ 正确。
所以答案为 D
计组