10-1 电流 电动势
恒定磁场(绪论)
•静止电荷——静电场
•运动电荷——电场、磁场
•稳恒电流产生的磁场不随时间变化——稳恒磁场
10.1.1 磁现象及其规律
磁性
天然磁石和人工磁铁吸收铁(Fe),钴( Co),镍(Ni)的性质。
磁体——具有磁性的物体
永久磁体——长期保持磁性的物体
磁极
条形磁铁两端磁性最强的部分
在水平面内自由转动的条形磁铁,在平衡时总是指向南北方向的,分别称为磁铁的两极(N、S)。
不存在磁单极
10.1.2电流的磁效应

小结:
•运动电荷会激发磁场;
•运动的电荷在电磁场中将受到磁场力的作用;
•一切磁现象起源于电荷的运动,磁场力就是运动电荷之间的一种相互作用力。
内容:
•描述磁场的基本物理量——磁感应强度
•电流磁场的基本方程——Biot-savart定律
•磁场性质的基本方程——高斯定理与安培环路定理
•磁场对电流与运动电荷的作用——Lorentz力、Ampere力
10.1.3 恒定电流
静电场中的导体处于静电平衡时,其内部的场强为零,内部没有电荷作定向的宏观运动。
如果把导体接在电源的两极上,则导体内任意两点之间将维持恒定的电势差,在导体内维持一个电场,导体内的电荷在电场力的作用下作宏观的定向运动,形成电流。
一、电流
1、形成电流的条件
•在导体内有可以自由移动的电荷(载流子)
在半导体中是电子或空穴
在金属中是电子
在电解质溶液中是离子
•在导体内要维持一个电场,或者说在导体两端要存在有电势差
2、电流的方向
正电荷移动的方向定义为电流的方向
电流的方向与自由电子移动的方向是相反的。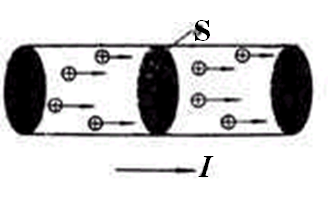
3、电流强度
单位时间内通过任一截面S的电量,叫做电流强度
是表示电流强弱的物理量,是标量,用 I 表示。
单位:库仑/秒=安培
国际单位制基本量
毫安(mA)、微安(mA)
二、电流密度
1、引入电流密度的必要性:
描述电流分布的物理量——电流密度。
2、定义:
电流密度矢量的**方向为空间某点处正电荷的运动方向, 它的大小**等于单位时间内该点附近垂直与电荷运动方向的单位截面上所通过的电量。
方向:该点正电荷运动方向
大小:单位时间内过该点且垂直于正电荷运动方向的单位面积的电荷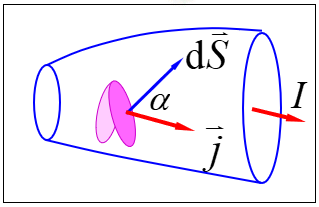
通过任意截面的电流
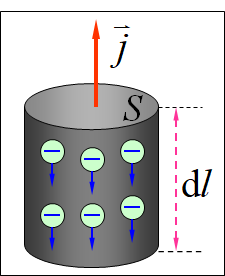
3、电流和电流密度与电子漂移速度的关系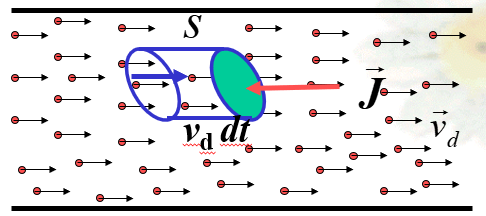
•n——导体中自由电子的数密度
•e——电子的电量
•——假定每个电子的漂移速度
在时间间隔内,长为
、横截面积为S 的圆柱体内的自由电子都要通过横截面积
,所以此圆柱体内的自由电子数为
,电量为
通过此导体的电流强度为

10.1.4 电源 电动势
一、电源
1、电源
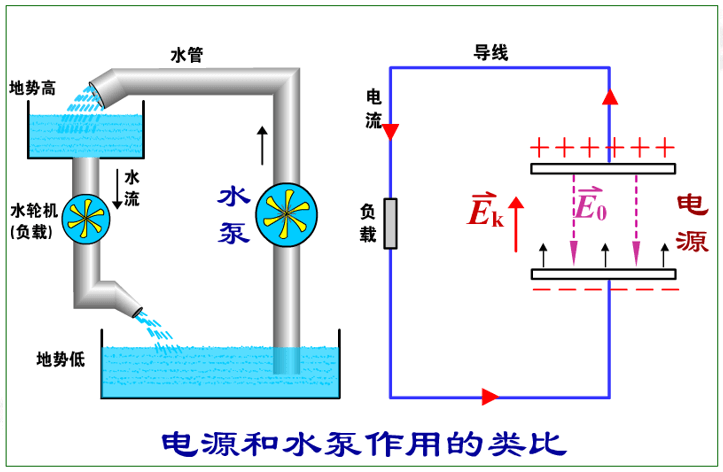
在导体中有稳恒电流流动就不能单靠静电力,必须有非静电力把正电荷从负极板搬到正极板才能在导体两端维持有稳恒的电势差。这种能够提供非静电力的装置叫作电源。电源的作用是把其它形式的能量转变为电能。
静电力欲使正电荷从高电位到低电位。
非静电力欲使正电荷从低电位到高电位。
2、电源的种类
电解电池、蓄电池——化学能→电能
光电池 ——光能 →电能
发电机 ——机械能→电能
电源内部电流从负极板到正极板叫内电路
电源外部电流从正极板到负极板叫外电路
二、电动势
1、引入
为了表述不同电源转化能量的能力,引入了电源电动势这一物理量。
2、定义
把单位正电荷绕闭合回路一周时,电源非静电力做的功定义为电源的电动势。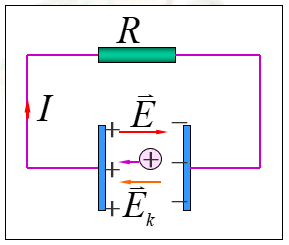
非静电力电场强度
3、计算
因为电源外部没有非静电力,所以可写为:
电源电动势的大小等于把单位正电荷从负极经电源内部移到正极时非静电力所作的功。
4、电源的表示法
电势高的地方为正极,电势低的地方为负极。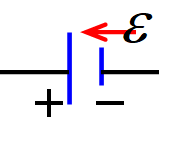
5、说明:
•电动势是标量,但有方向;其方向为电源内部电势升高的方向,即从负极经电源内部到正极的方向为电动势的方向。
•电动势的大小只取决于电源本身的性质,而与外电路无关。
•电动势的单位为伏特。
•电源内部也有电阻,称为内阻。
•电源两极之间的电势差称为路端电压,与电源的电动势是不同的。
10-2 磁场 磁感应强度 毕奥-萨伐尔定律
10.2.1 磁场
1、概念
在运动电荷(或电流)周围空间存在的一种特殊形式的物质。
2、磁场的特性
•磁场对磁体、运动电荷或载流导线有磁场力的作用;
•载流导线在磁场中运动时,磁场力要作功——磁场具有能量。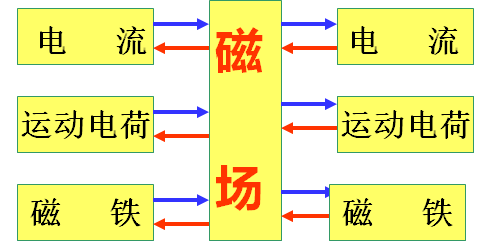
10.2.2 磁感应强度
1、引入
需要一个既具有大小又有方向的物理量来定量描述磁场。
2、实验:运动电荷在磁场中的受力情况

实验结果:带电粒子在磁场中运动所受的力与运动方向有关.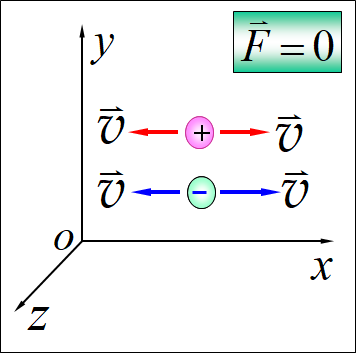
1、实验发现,带电粒子在磁场中沿某一特定方向运动时不受力,此方向与电荷无关.
2、带电粒子在磁场中沿其他方向运动时, 垂直于与特定直线所组成的平面.
3、当带电粒子在磁场中垂直于此特定直线运动时受力最大.
大小与
无关
3、磁感应强度的定义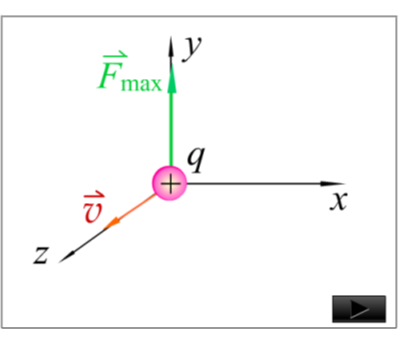
•磁场中任一点都存在一个特殊的方向和确定的比值
•反映了磁场在该点的方向特征和强弱特征
•定义矢量函数B,规定:的方向:当电荷沿此方向或其反方向运动时所受的磁场力为零。
正电荷垂直于特定直线运动时,受力与电荷速度的叉积
方向:的大小:
讨论:
1.由
划分磁场为: 均匀磁场:空间各处的
大小相等,方向相同 非均匀磁场:空间各处的
大小或者方向不同
2.与
的区别
:方向为的方向,是矢量,是空间的点函数
:方向与正电荷受到的静电力
方向相同,是矢量,是空间的点函数大小上:表达式各不相同
、
都遵从矢量的叠加原理
3.运动电荷在磁场中受力单位:特斯拉


10.2.3 磁通量
一、磁感应线
1.磁感应线
•用来描述磁场分布的曲线。
•磁感应线上任一点切线的方向——B的方向。
•B的大小可用磁感应线的疏密程度表示。
磁感应线密度:在与磁感应线**垂直**的单位面积上的穿过的磁感应线的数目。
2、几种典型的磁感应线
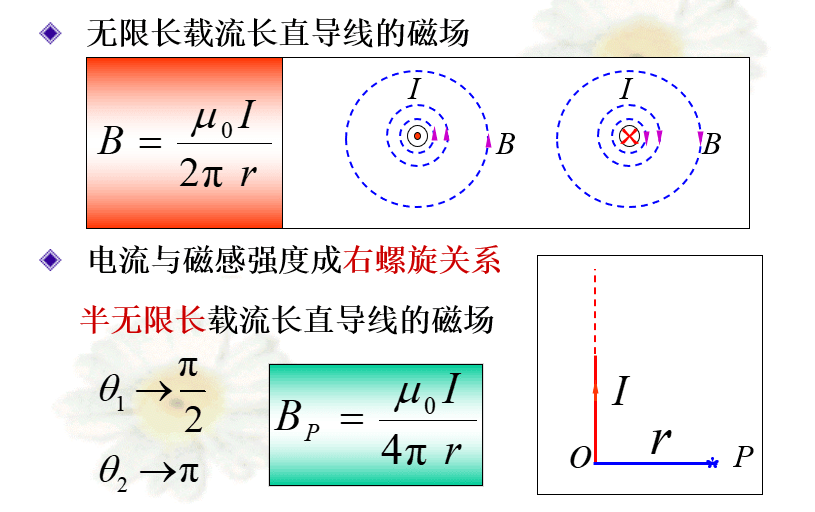
载流长直导线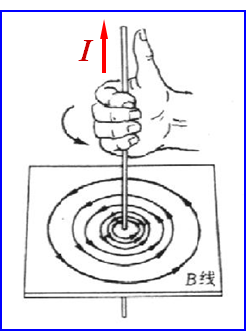
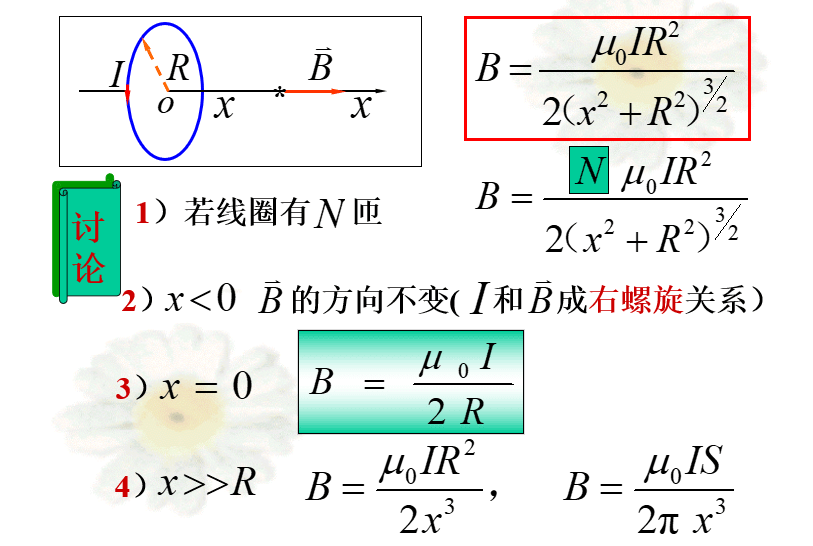
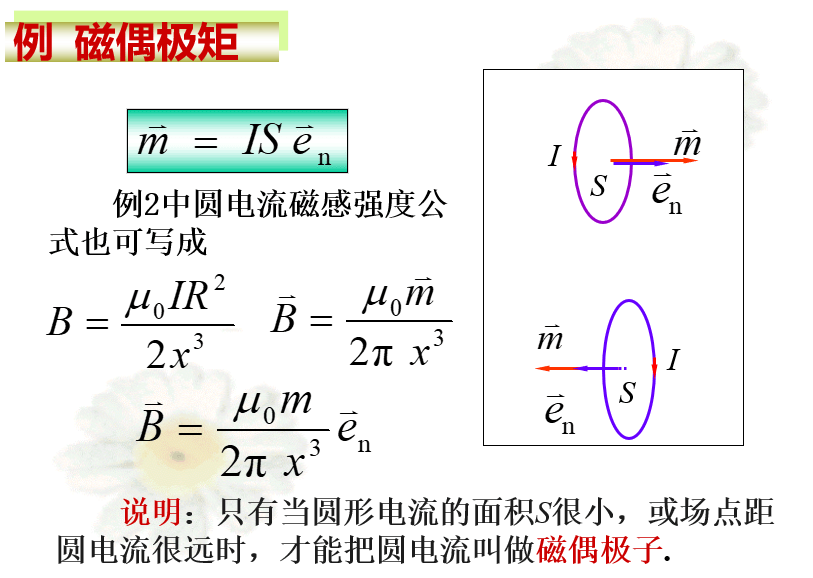
圆电流
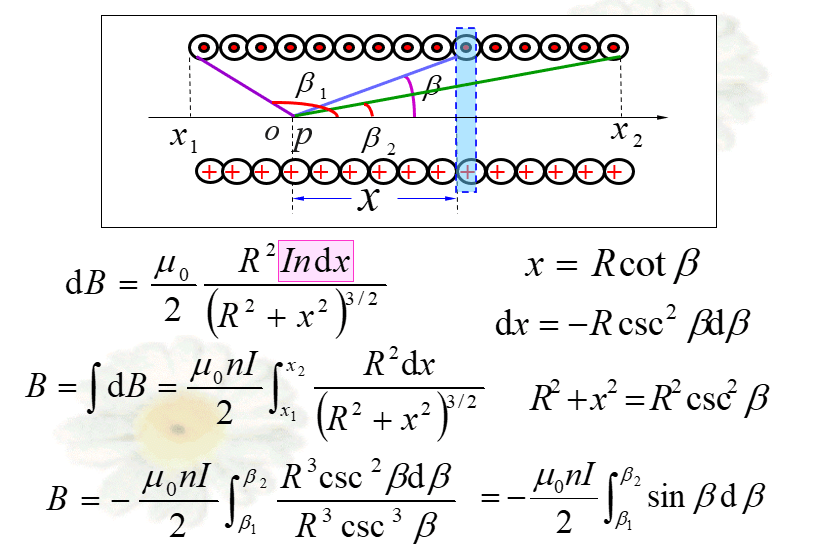
载流长螺线管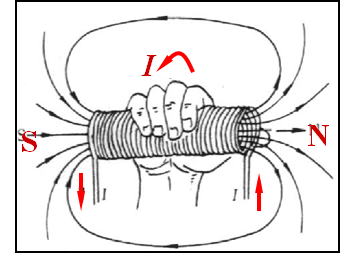
3、磁感应线特性
直线电流的磁感应线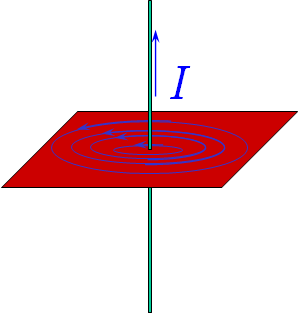
圆电流的磁感应线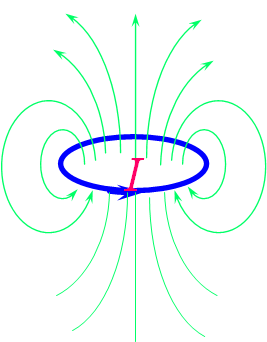
通电螺线管的感应线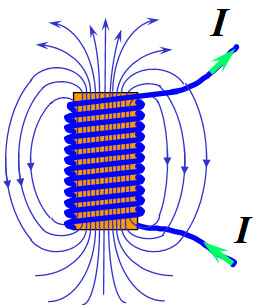
1)每一条磁感应线都是环绕电流的闭合曲线,都与闭合电路互相套合,因此磁场是涡旋场。磁感应线是无头无尾的闭合回线。
2)任意两条磁感应线在空间不相交。
3)磁感应线的环绕方向与电流方向之间可以分别用右手定则表示。
二、磁通量
1、磁通量定义:
通过磁场中某一曲面的磁感应线的数目,定义为磁通量,用表示。
2、计算
a.垂直
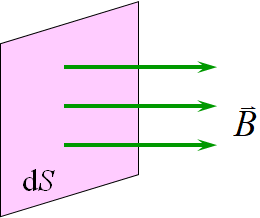
b.跟
成
角

c. 通过任一曲面的磁通量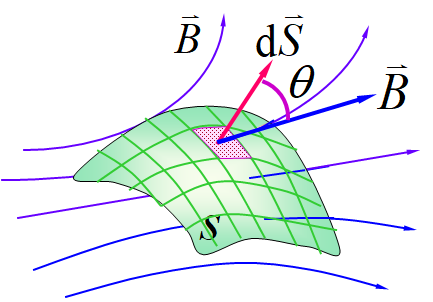
3、说明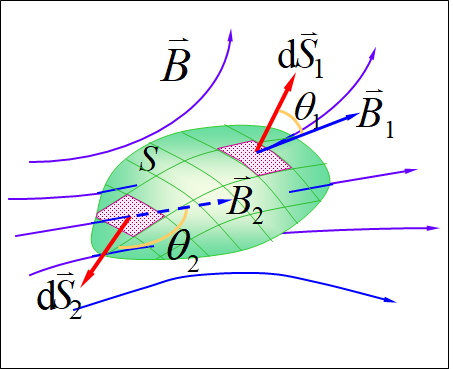
•规定n的方向垂直于曲面向外
磁感应线从曲面内穿出时,磁通量为正(θ<_π_/2, cos_θ_>0)
磁感应线从曲面出穿入时,磁通量为负(θ>π/2, cosθ<0)
•穿过曲面通量可直观地理解为穿过该面的磁感应线条数
•单位:韦伯(wb)
10.2.4 高斯定理
1、内容
通过任意闭合曲面的磁通量必等于零。
2、解释
磁感应线是闭合的,因此有多少条磁感应线进入闭合曲面,就一定有多少条磁感应线穿出该曲面。
3、说明
•磁场是有旋/无散场(非保守场); 电场是有源场,保守场
•磁极相对出现,不存在磁单极; 单独存在正负电荷
10.2.5 毕奥-萨伐尔定律
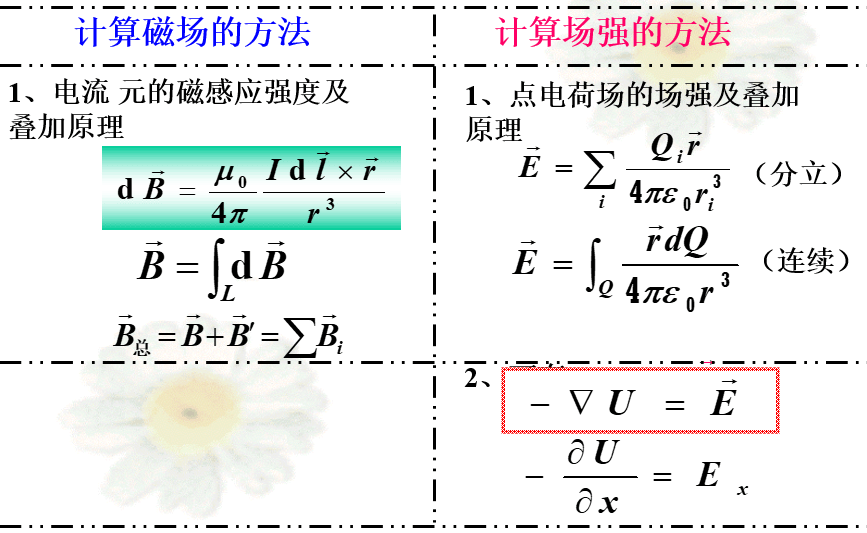
一、毕奥-萨伐尔定律
1、引入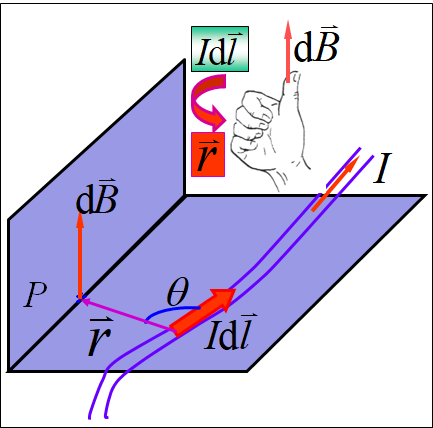
毕奥-萨伐尔根据电流磁作用的实验结果分析得出,电流元产生磁场的规律称为毕奥-萨伐尔定律。
2、内容
电流元I_d_l在空间P点产生的磁场B为:称为真空磁导率
3、 叠加原理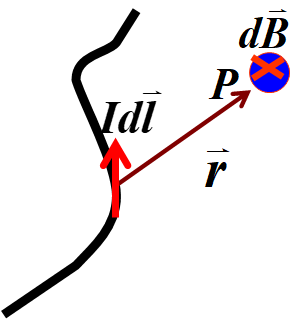
任一电流产生的磁场
4、说明
•该定律是在实验的基础上抽象出来的,不能由实验直接证明,但是由该定律出发得出的一些结果,却能很好地与实验符合。
•电流元I_d_l的方向即为电流的方向;
•dB的方向由I_d_l确定,即用右手螺旋法则确定;
•毕奥-萨伐尔定律是求解电流磁场的基本公式,利用该定律,原则上可以求解任何稳恒载流导线产生的磁感应强度。


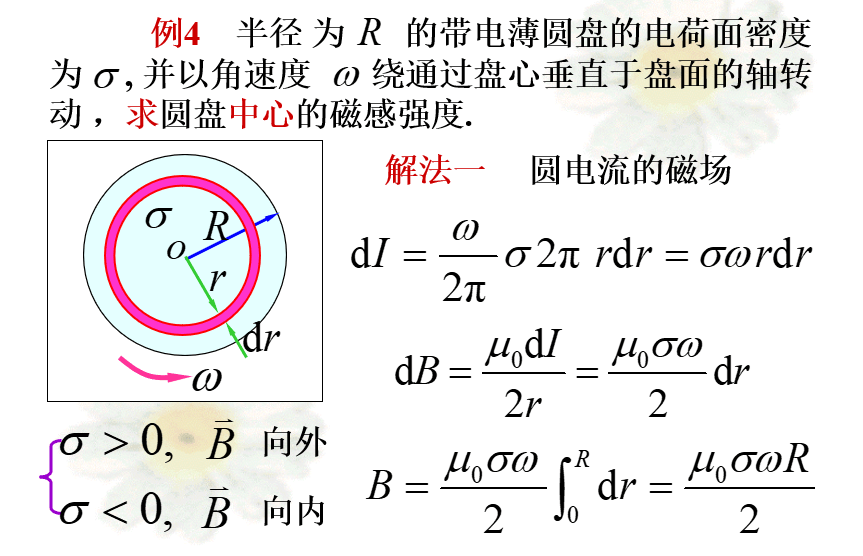
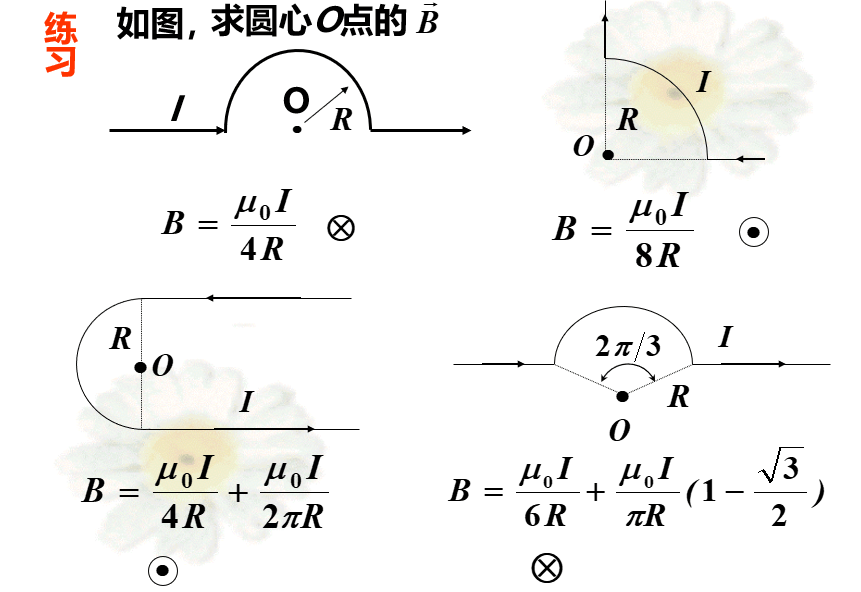
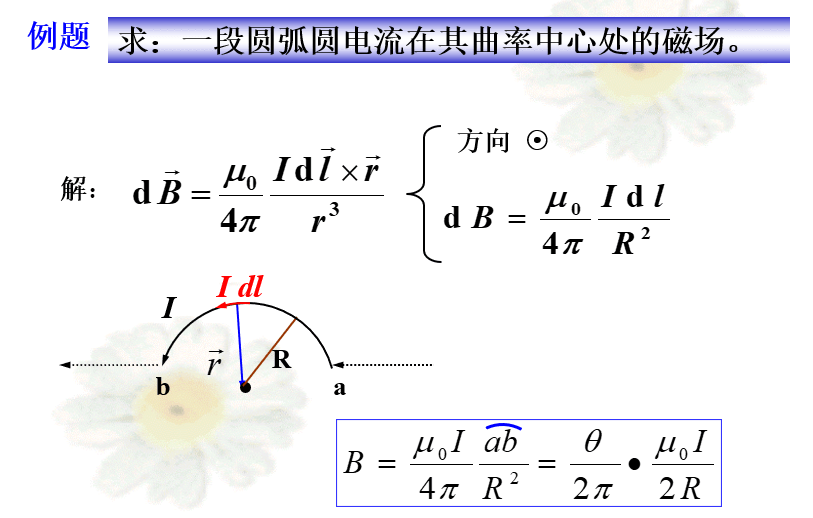
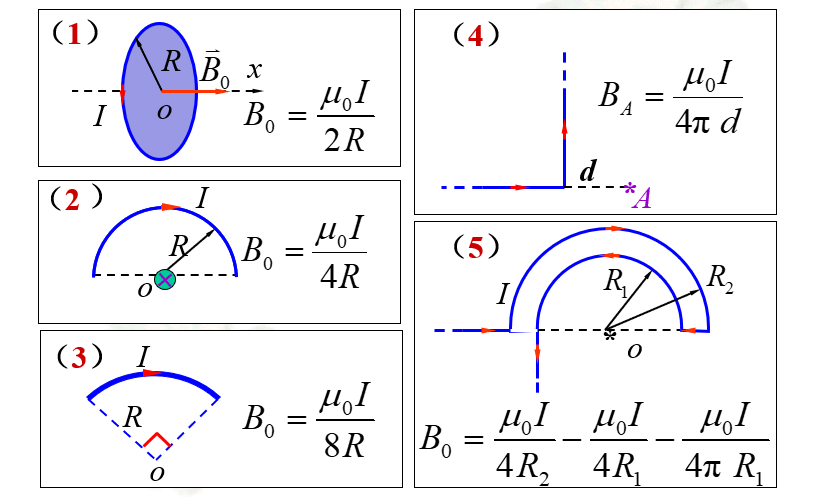
10.2.6 毕奥-萨伐尔定律应用举例
解题步骤
1.选取合适的电流元——根据已知电流的分布与待求场点的位置;
2.写出电流元产生的磁感应强度——根据毕奥-萨伐尔定律;
3.选取合适的坐标系——要根据电流的分布与磁场分布的特点来选取坐标系,其目的是要使数学运算简单;
4.计算磁感应强度的分布——叠加原理;
一般说来,需要将磁感应强度的矢量积分变为标量积分,并选取合适的积分变量,来统一积分变量。
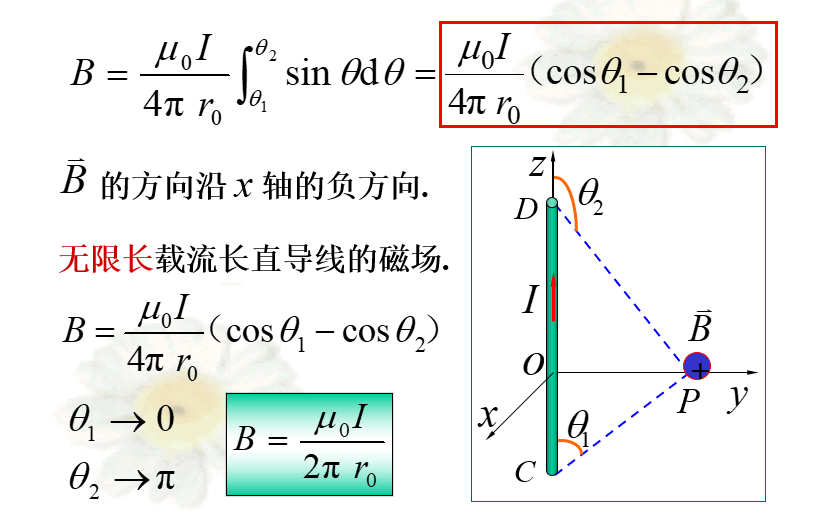

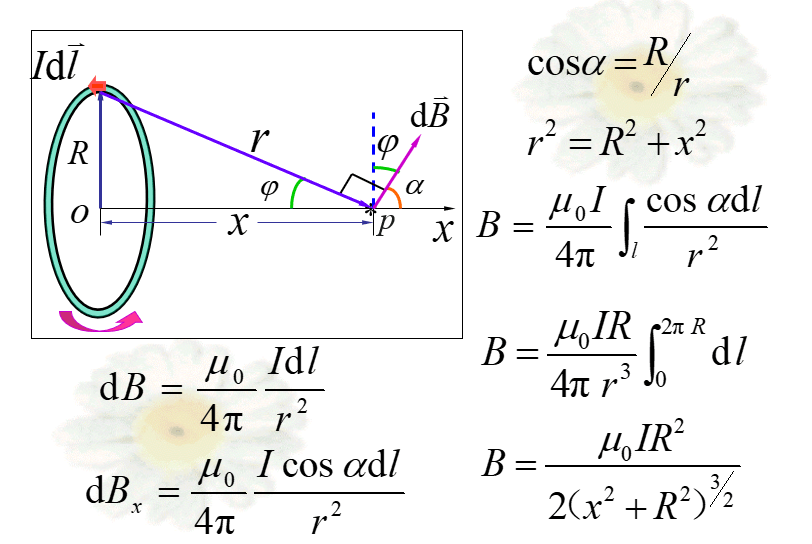



10.2.7 运动电荷的磁场
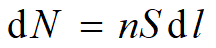

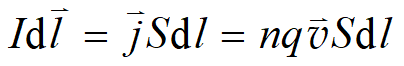
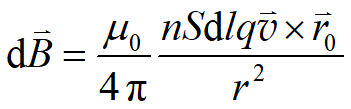

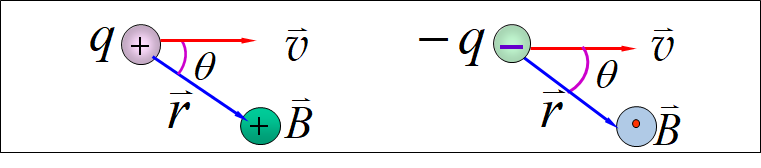
小 结
10-3 安培环路定理
安培 (Ampere, 1775-1836)
法国物理学家,电动力学的创始人。1805年担任法兰西学院的物理教授,1814年参加了法国科学会,1818年担任巴黎大学总督学,1827年被选为英国皇家学会会员。他还是柏林科学院和斯德哥尔摩科学院院士。
安培在电磁学方面的贡献卓著,发现了一系列的重要定律、定理,推动了电磁学的迅速发展。1827年他首先推导出了电动力学的基本公式,建立了电动力学的基本理论,成为电动力学的创始人。
10.3.1 安培环路定理
1、内容

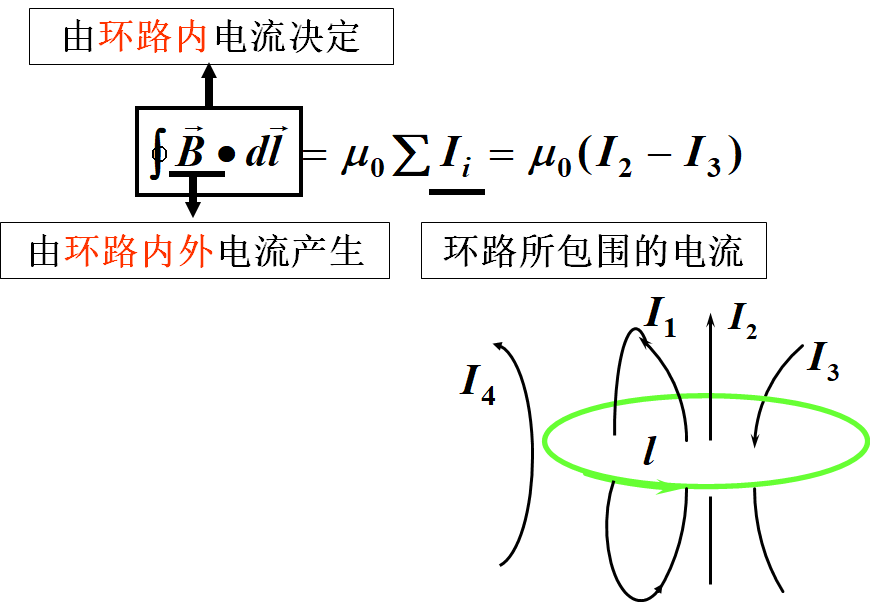
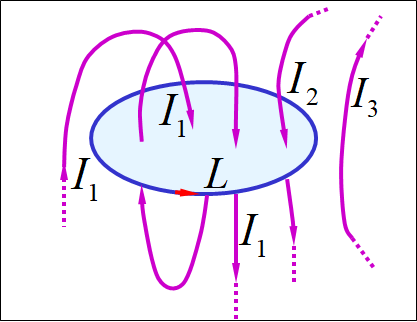
在真空稳恒电流的磁场中,磁感应强度B沿任何闭合回路L的线积分,等于穿过这回路的所有电流强度代数和的倍,数学表达式:
电流正负的规定––– 按右手螺旋法则。
2、证明
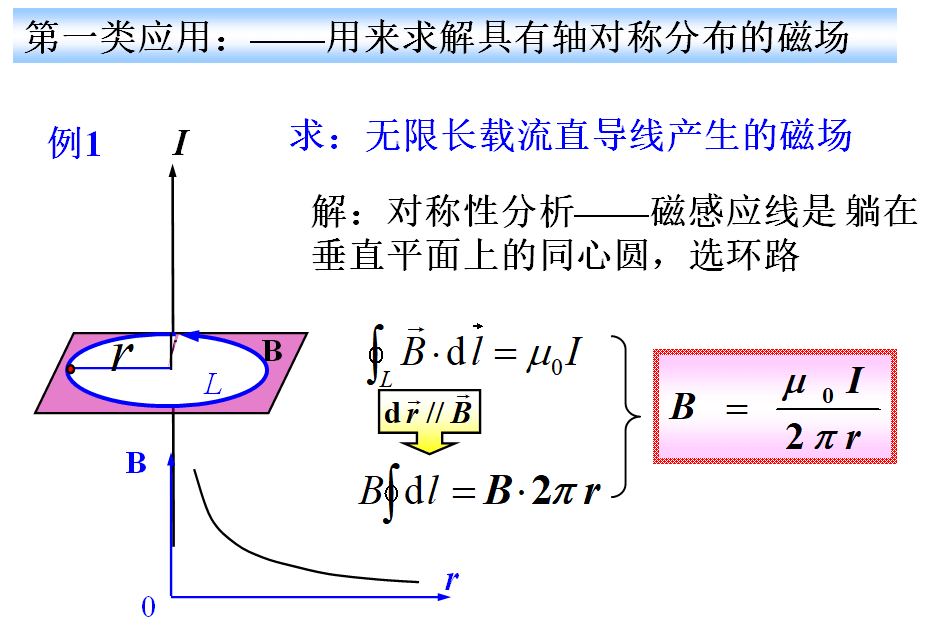
(1)在围绕单根载流导线的垂直平面内的圆形回路。
设闭合回路为圆形回路(
与
成右螺旋)

若回路绕向化为顺时针时,则
(2)在围绕单根载流导线的垂直平面内的任一回路。
(3)不围绕单根载流导线,在垂直平面内的任一回路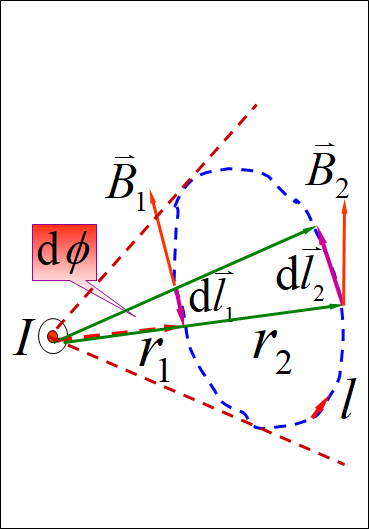
(4)围绕多根载流导线的任一回路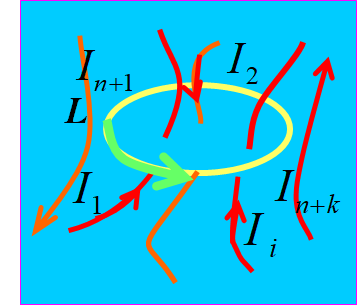
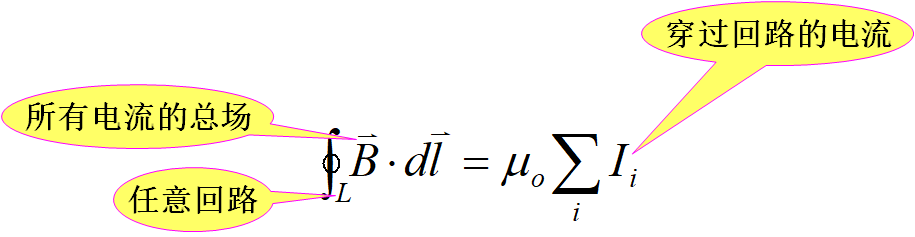
安培环路定理
即在真空的稳恒磁场中,磁感应强度沿任一闭合路径的积分的值,等于
乘以该闭合路径所包围的各电流的代数和.
注意
电流正负的规定 :
与
成右螺旋时,
为正;反之为负.
3、说明
•符号规定:电流方向与L的环绕方向服从右手关系的 I为正,否则为负。
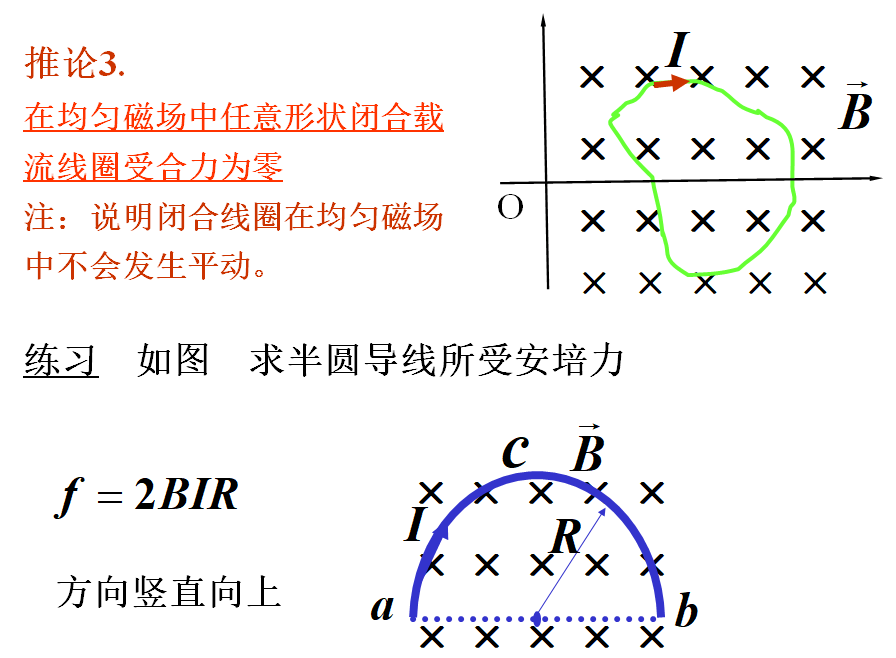
•安培环路定律对于任一形状的闭合回路均成立。
•B的环流与电流分布有关,但路径上B仍是闭合路径内外电流的合贡献。
•物理意义:磁场是非保守场,不能引入势能。
10.3.2 安培环路定理的应用
1.分析磁场的对称性:根据电流的分布来分析;
2.过场点选取合适的闭合积分路径;
3.选好积分回路的取向,确定回路内电流的正负;
4.由安培环路定理求出B。
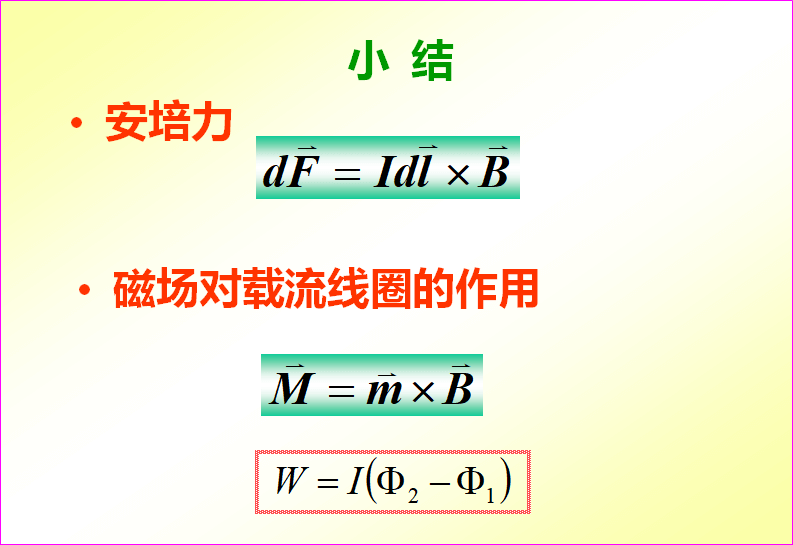
10-4磁场对载流导线的作用
10.4.1 安培力
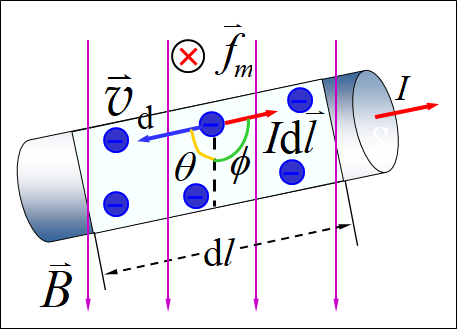
电子在磁场中受力——洛仑兹力
电流元在磁场中所受的力等于
个电子所受的力
由于自由电子与晶格之间的相互作用,使导线在宏观上看起来受到了磁场的作用力 .
安培定律 磁场对电流元的作用力:
意义 磁场对电流元作用的力 ,在数值上等于电流元的大小 、电流元所在处的磁感强度
大小以及电流元和磁感应强度之间的夹角
的正弦之乘积 ,
垂直于
和
所组成的平面, 且
与
同向 .

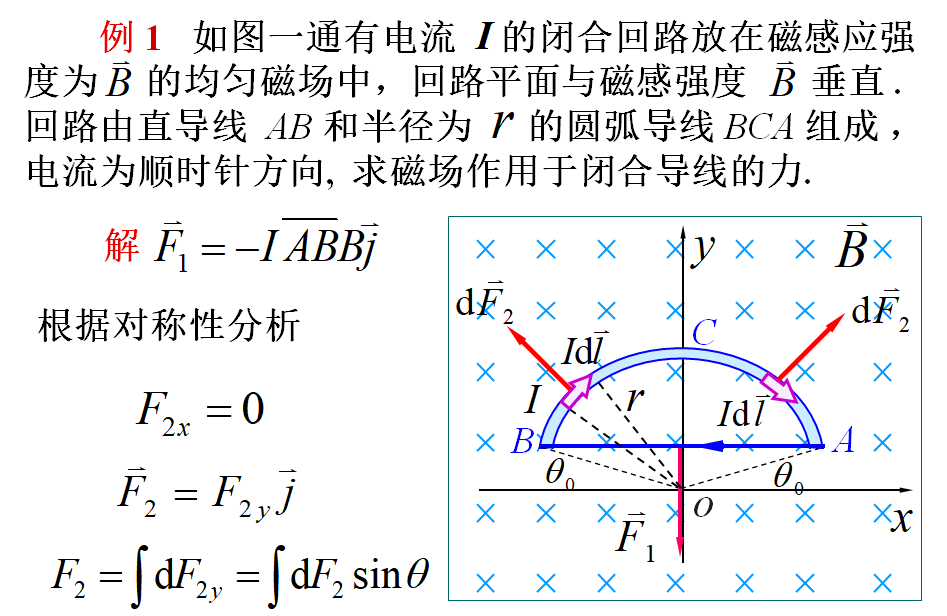
有限长载流导线所受的安培力
10.4.2、电流的单位 平行电流间的相互作用
1、平行载流直导线间的相互作用
问题:两平行长直载流导线,相距为 d
求:每单位长度线段所受的作用力。
电流 在电流
处所产生的磁场为:
导线2上长度受力为
电流 在电流
处所产生的磁场为:
2、电流强度的单位:
在其空中有两根平行的长直线,它们之间相距1m,两导线上电流流向相同,大小相等,调节它们的电流,使得两导线每单位长度上的吸引力为,我们就规定这个电流为1A。
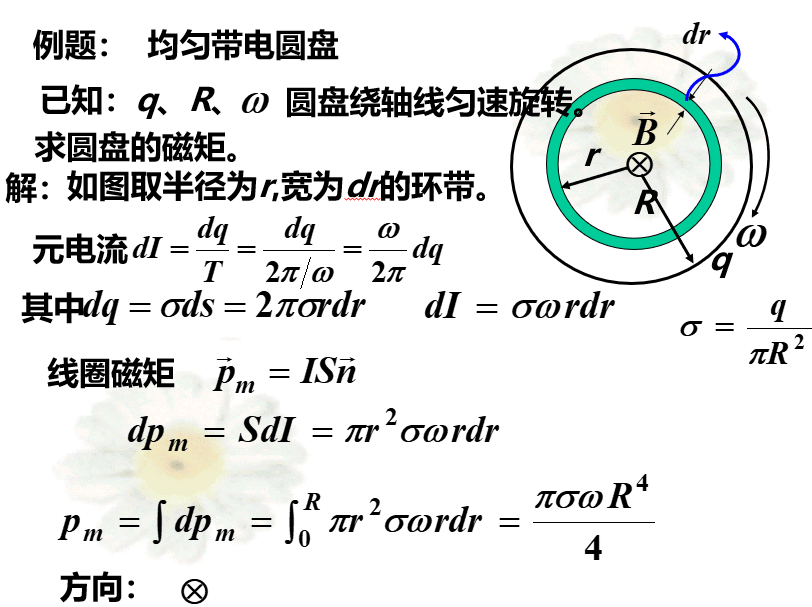
10.4.3 磁场作用于载流线圈的磁力矩
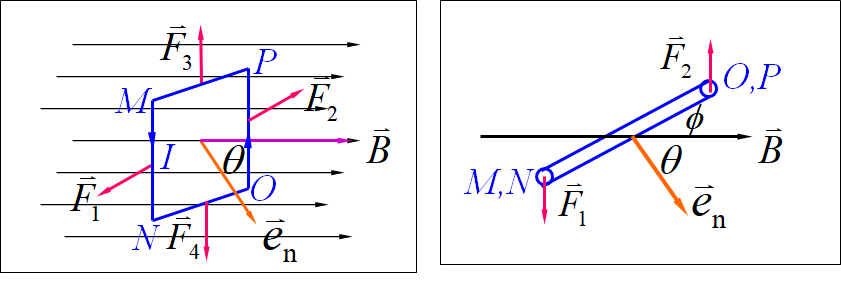
•受力情况
两者大小相等,方向相反,且在同一直线上,故对于线圈来说,它们合力矩为零。与
形成一个力偶
10.4.4 磁力的功
1. 载流导线在磁场中运动时磁力所做的功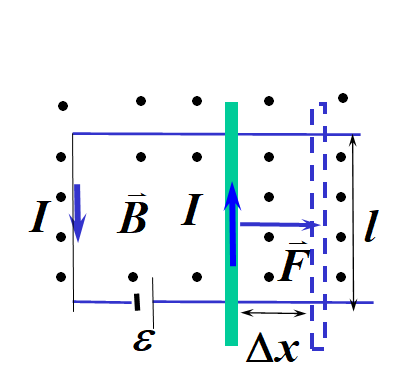
2.载流线圈在磁场中转动时磁力矩所做的功

磁力矩总是力图使转向B,磁力矩做负功。
当 不随时间变化,




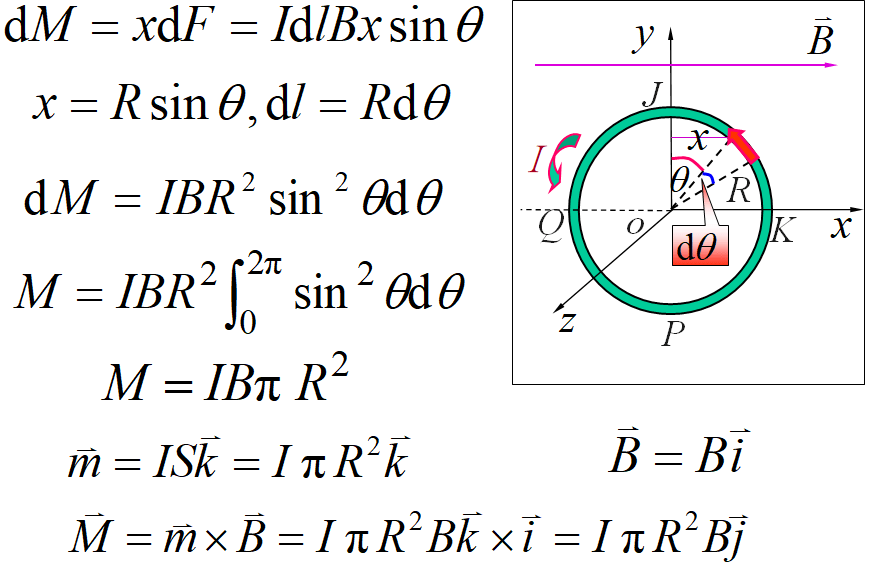

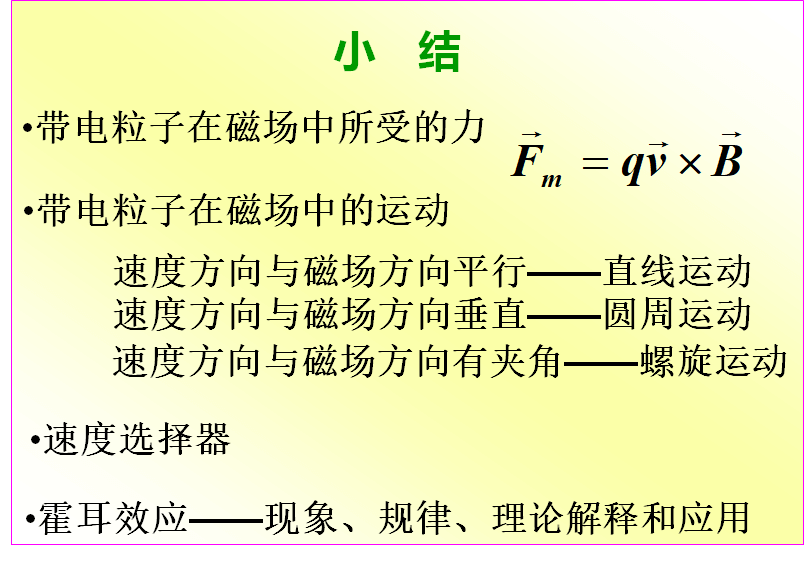
10-5 带电粒子在电场和磁场中的运动
10.5.1带电粒子在电场和磁场中所受的力
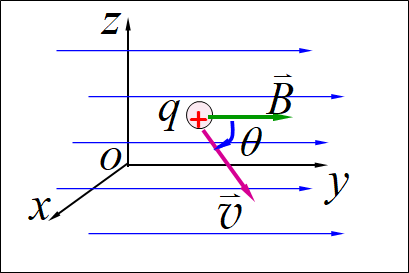
电场力:
磁场力(洛伦兹力)
大小:
方向:与及
有关
运动电荷在电场和磁场中受的力:
洛仑兹(Hendrik Antoon Lorentz, 1853-1928)
荷兰物理学家、数学家,因研究磁场对辐射现象的影响取得重要成果,与塞曼共获1902年诺贝尔物理学奖金。 1895年,洛仑兹根据物质电结构的假说,创立了经典电子论。洛仑兹的电磁场理论研究成果,在现代物理中占有重要地位。洛仑兹力是洛仑兹在研究电子在磁场中所受的力的实验中确立起来的。 洛仑兹还预言了正常的塞曼效益,即磁场中的光源所发出的各谱线,受磁场的影响而分裂成多条的现象中的某种特殊现象。 洛仑兹的理论是从经典物理到相对论物理的重要桥梁,他的理论构成了相对论的重要基础。洛仑兹对统计物理学也有贡献。
10.5.2 带电粒子在磁场中的运动
1、速度方向与磁场方向平行或反平行
2、速度方向与磁场方向垂直
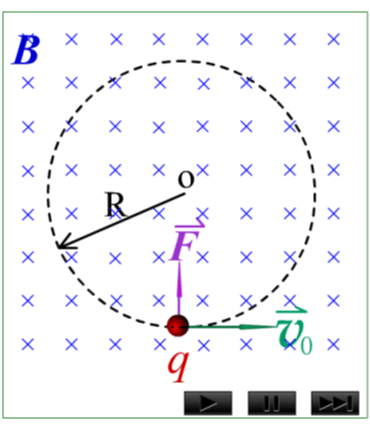
洛仑兹力的大小:
方向:垂直与速度和磁场的方向
结论:带电粒子作匀速圆周运动。
回旋半径:
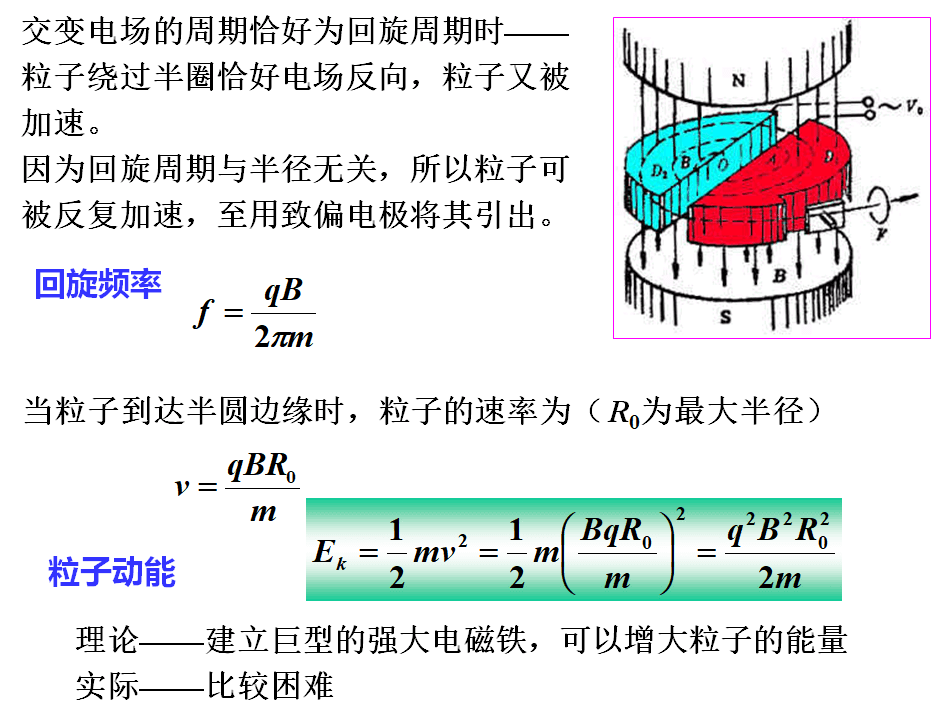
回旋周期:
回旋频率:
3、速度方向与磁场方向有夹角
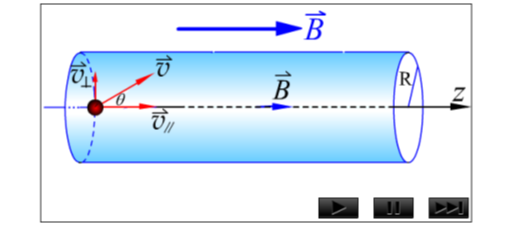
把速度分解成平行于磁场的分量与垂直于磁场的分量
平行于磁场的方向: , 匀速直线运动
垂直于磁场的方向: , 匀速圆周运动
粒子作螺旋线向前运动,轨迹是螺旋线。
回旋半径:
回旋周期:
螺距——粒子回转一周所前进的距离:
10.5.3 带电粒子在电场和磁场中的运动举例
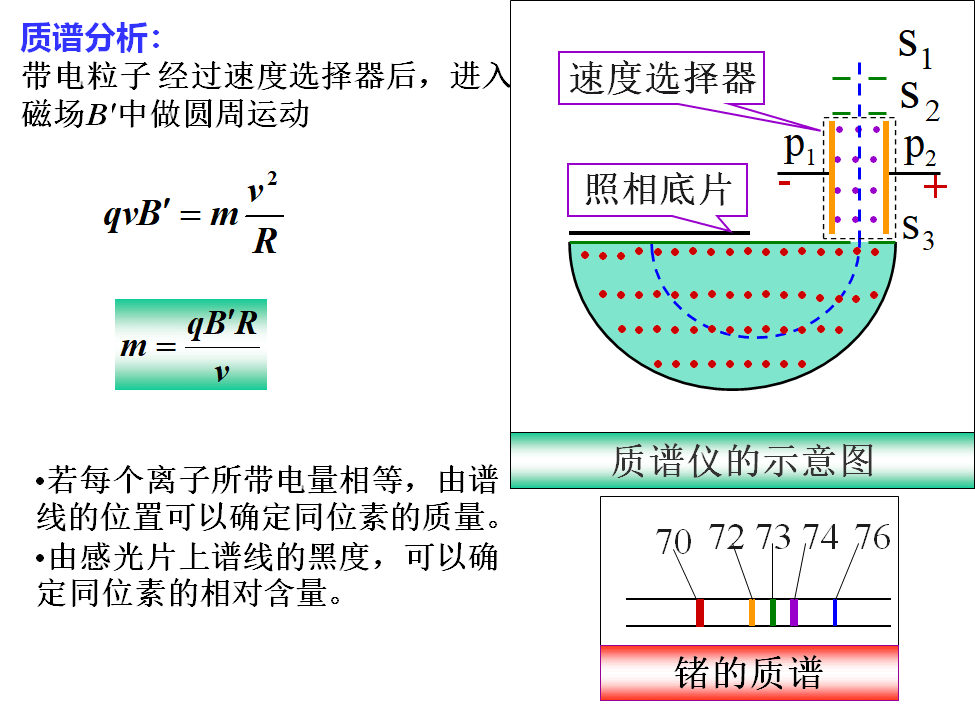
1、质谱仪 •引言:是用物理方法分析同位素的仪器,由英国物理学家与化学家阿斯顿于1919年创造,当年发现了氯与汞的同位素,以后几年又发现了许多同位素,为此,阿斯顿于1922年获诺贝尔化学奖。 •原理图
速度选择器 从离子源出来的离子经过
加速进入电场和磁场空间,若粒子带正电荷+q,则电荷所受的力有: 洛仑兹力:
电场力 :
若粒子能进入下面的磁场







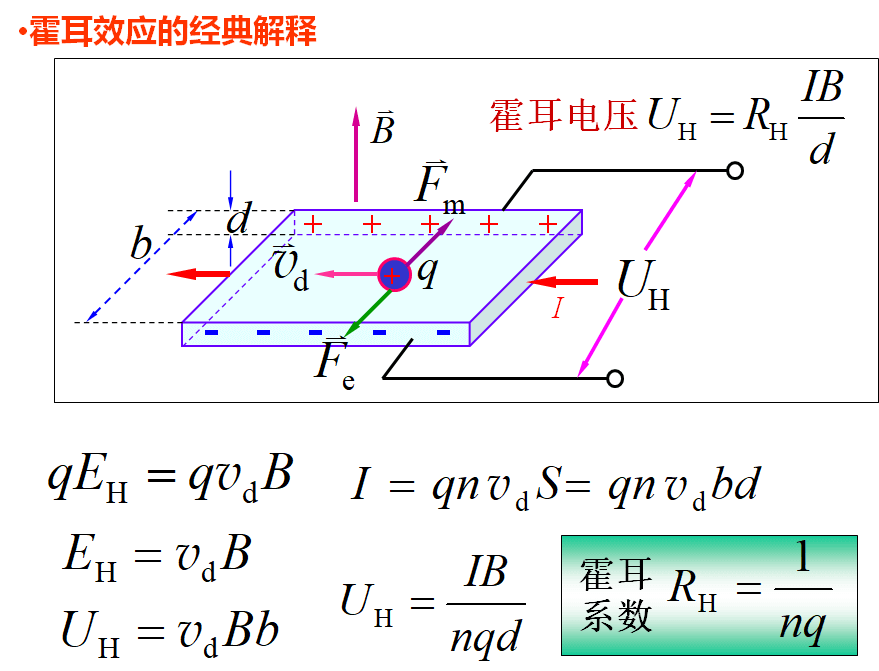
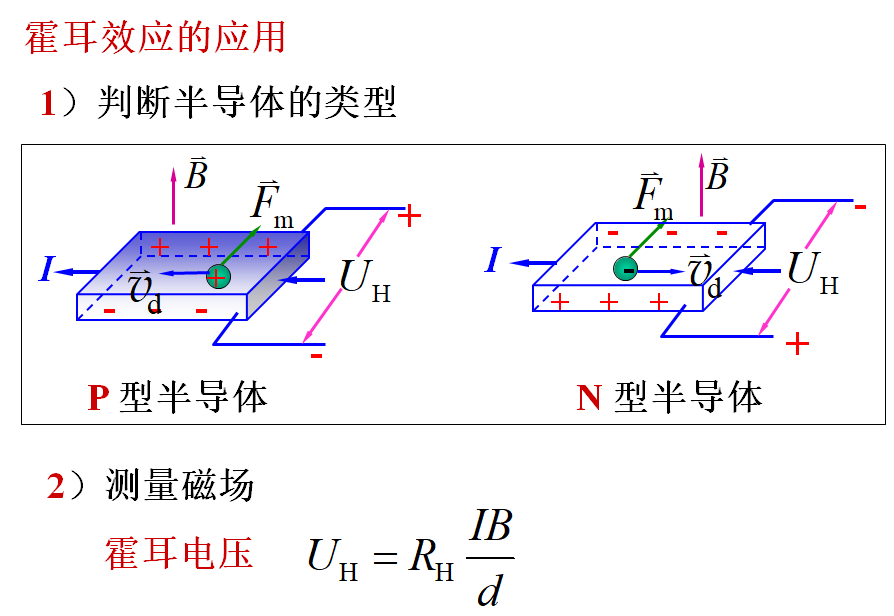
10-6 磁介质
磁场中的磁介质
讨论磁场和磁介质的相互作用:
•磁介质的三种类型:
顺磁质、抗磁质、铁磁质
•磁介质对磁场的影响
•磁场强度、磁化强度及其规律
•铁磁质的特性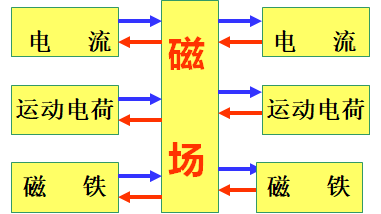
10.6.1 磁介质
1、什么是磁介质
能够磁化的物质称作磁介质。
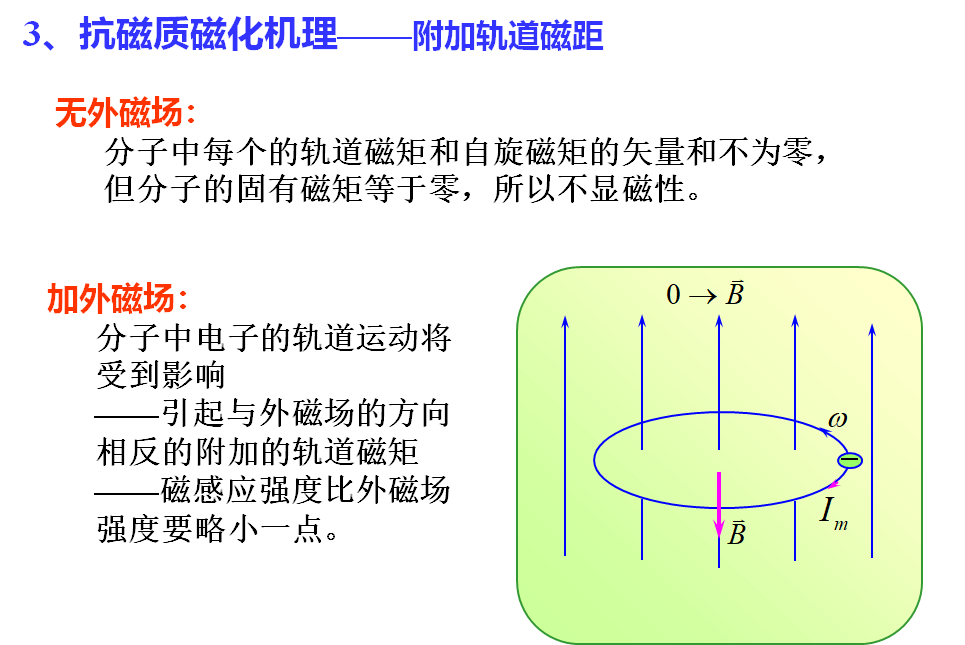
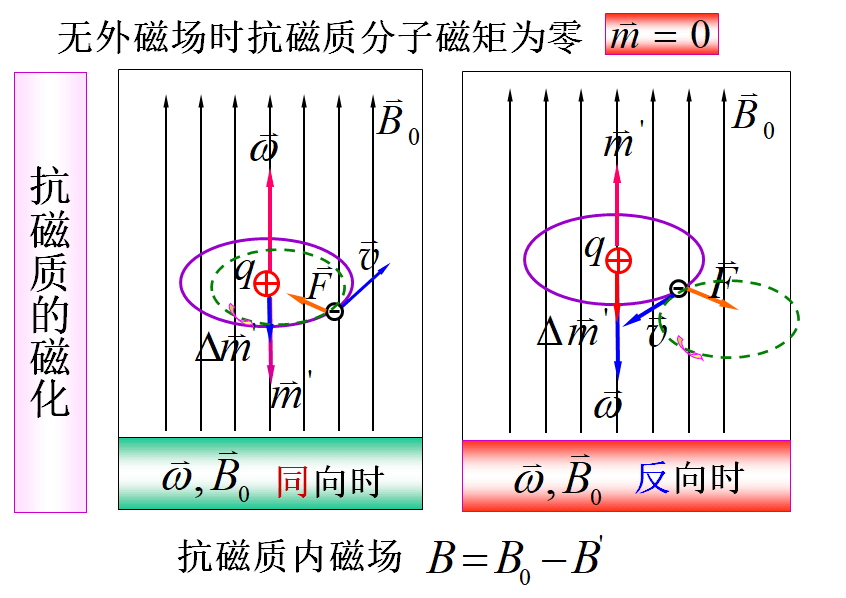
2、磁介质的磁化
3、磁介质的分类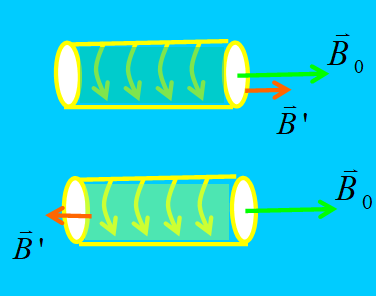
标准——与
方向
顺磁质与
同向,
,
如氧、铝、钨、铂、铬等
抗磁质与
反向,
,
如氮、水、铜、银、金、铋等。
铁磁质与
同向,
,
如铁、钴、镍等。
顺磁质和抗磁质又称为弱磁质。
10.6.2 磁介质的磁化*
10.6.3 磁化强度*
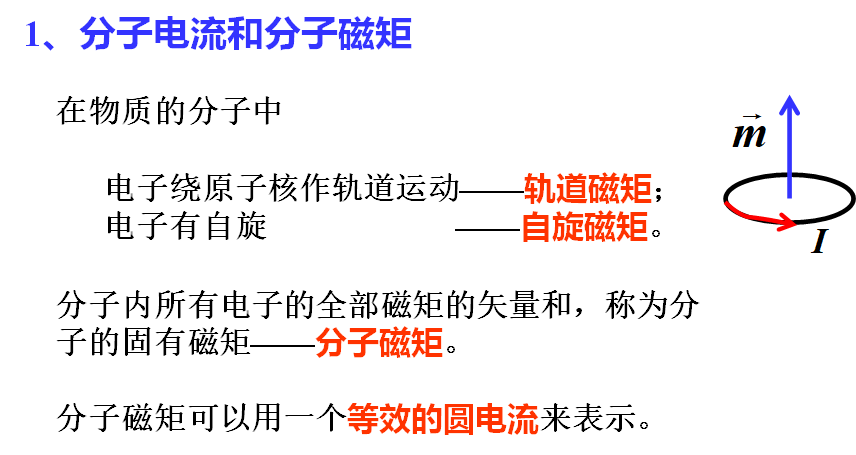
1、引入:
用单位体积内的分子磁矩的矢量和来描述磁介质磁化的程度。
2、定义:
磁介质中单位体积内的合磁矩的矢量和,称为磁化强度。
3、单位:
安培/米 ()
4、说明:
•磁化强度是描述磁介质的宏观量
•与介质特性、温度与统计规律有关
10.6.4有磁介质时的磁高斯定理
磁介质存在时,磁感应线仍是一系列无头无尾的闭合曲线
对于任意闭合曲面S
10.6.5 磁介质中的安培环路定理 磁场强度
一、磁介质中的安培环路定律
1、问题:
长直螺线管
管中充满磁化强度为M 的各向同性的均匀磁介质
线圈中的电流为I
计算螺线管内磁介质中的磁感应强度。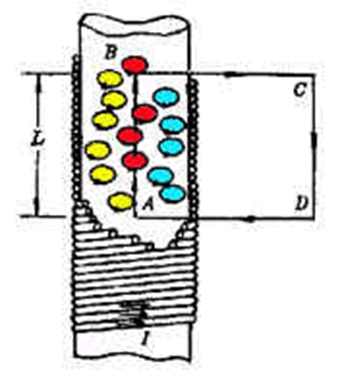
取闭合回路ABCDA
2、分布电流(磁化电流)
只有分子圆电流中心距直线AB的距离小于r 的分子圆电流才对 有贡献。
圆电流①——没有贡献,在闭合路径之外
圆电流②——有贡献
圆电流③——无贡献,流出流入代数和为0
3、磁介质中的安培环路定律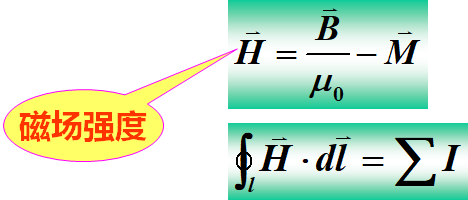
磁介质中的安培环路定理:磁场强度沿任何闭合回路的线积分,等于通过该回路所包围的传导电流的代数和。
4、说明
•磁场强度是一个辅助物理量。
•磁场强度单位:A· m^-1
•磁场强度的环流只与穿过闭合回路的传导电流有关,而与磁化电流无关。
二、磁场强度与磁感应强度的关系
1、定义式
.2、磁场强度与磁感应强度的关系
3、引进磁场强度的物理意义
在磁介质中,磁场强度的环流为
在磁介质中,磁感应强度的环流为
毕-萨定律
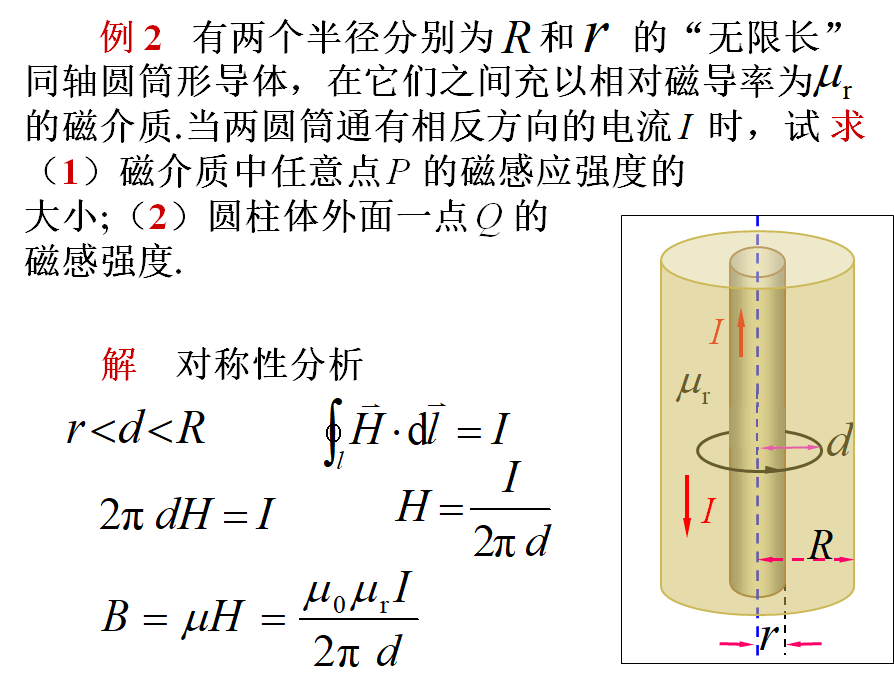
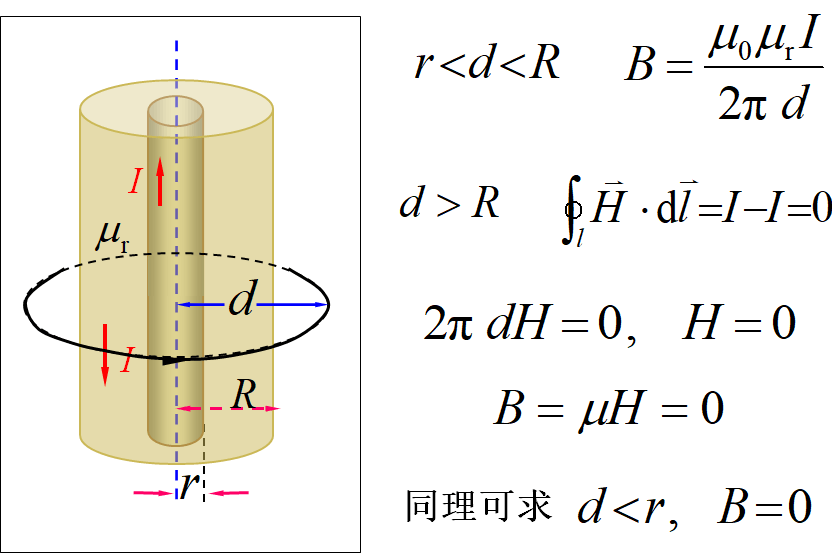
三、安培环路定律的应用
计算有磁介质存在时的磁感应强度
•求出磁场强度后
•由求磁感应强度
。

10.6.6 铁磁质
铁磁质的特性:
1.在外磁场作用下能产生很强的磁感应强度;
2.当外磁场停止作用时,仍能保持其磁化状态;
3.B与H之间不是简单的线性关系;
4.铁磁质都有一临界温度。
在此温度之上,铁磁性完全消失而成为顺磁质——居里温度或居里点。
铁——
镍——
钴——
铁磁质的起因可以用“磁畴”理论来解释。
一、磁畴
•概念:
在无外磁场的作用下磁畴取向平均抵消,能量最低,不显磁性。
铁磁质内的电子之间因自旋引起的相互作用非常强烈,在铁磁质内部形成了一些微小自发磁化区域,叫做磁畴。
每一个磁畴中,各个电子的自旋磁矩排列得很整齐。
磁畴大小约为个原子/
。
•磁畴的显示:
磁畴的变化可用金相显微镜观测
二、磁化曲线

•装置:
环形螺绕环
•原理:
励磁电流 ;用安培定理得
高斯计实验测量B。
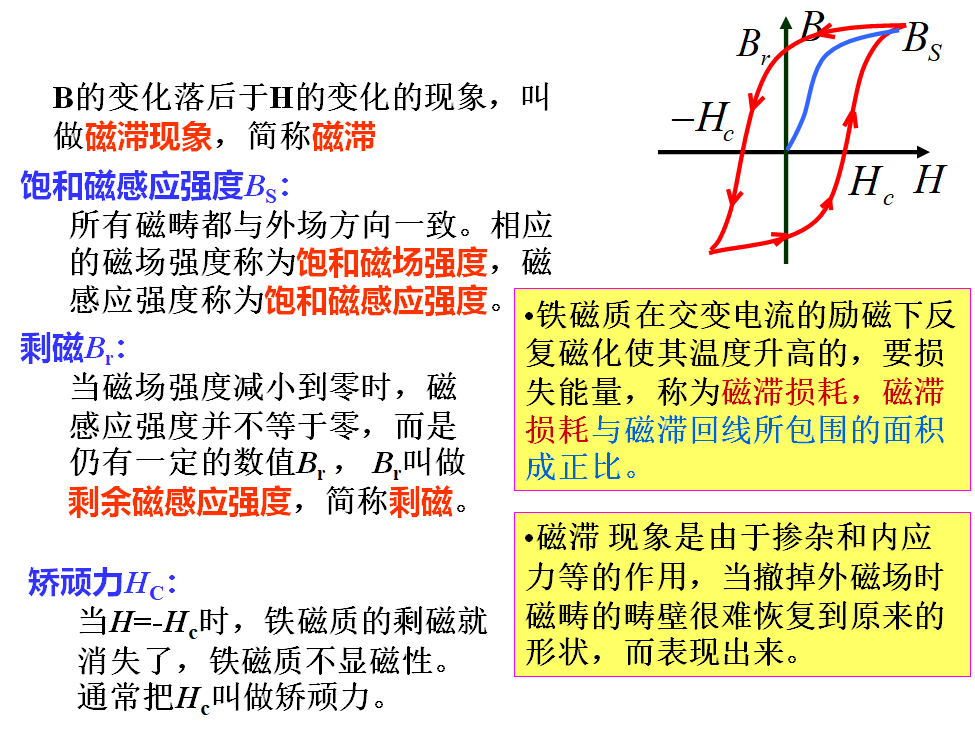
三、磁滞回线
四、铁磁性材料
1、金属磁性材料
软磁材料:
特点:相对磁导率和饱和B一般都较大,但矫顽力小,磁滞回线的面积窄而长,损耗小。易磁化、易退磁。
例子:如纯铁,硅钢坡莫合金,铁氧体等。
应用:适宜制造电磁铁、变压器、交流发电机、继电器、电机、以及各种高频电磁元件的磁芯、磁棒等。
硬磁材料:
特点:剩磁和矫顽力比较大,磁滞回线所围的面积大,磁滞损耗大,磁滞特性非常显著
例子:钨钢,碳钢,铝镍钴合金等。
应用:适合作永久磁铁,磁电式电表中的永磁铁,耳机中的永久磁铁,永磁扬声器。
2、非金属磁性材料——矩磁材料:
铁氧体,又叫铁淦氧,是由三氧化二铁和其它二价的金属氧化物的粉末混合烧结而成,常称为磁性瓷。如锰镁铁氧体、锂锰铁氧体等
特点: ,
不大,磁滞回线是矩形。
用途:用于记忆元件,当+脉冲产生使磁芯呈
态,则–脉冲产生
使磁芯呈
态,可做为二进制的两个态。
磁屏蔽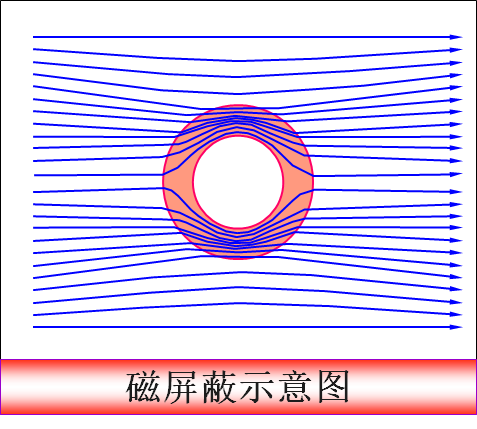
把磁导率不同的两种磁介质放到磁场中,在它们的交界面上磁场要发生突变,引起了磁感应线的折射.