斐波那契数列

求取斐波那契数列第N位的值。
斐波那契数列：每一位的值等于他前两位数字之和。前两位固定 0，1,1,2,3,5,8。。。。
解法一：暴力递归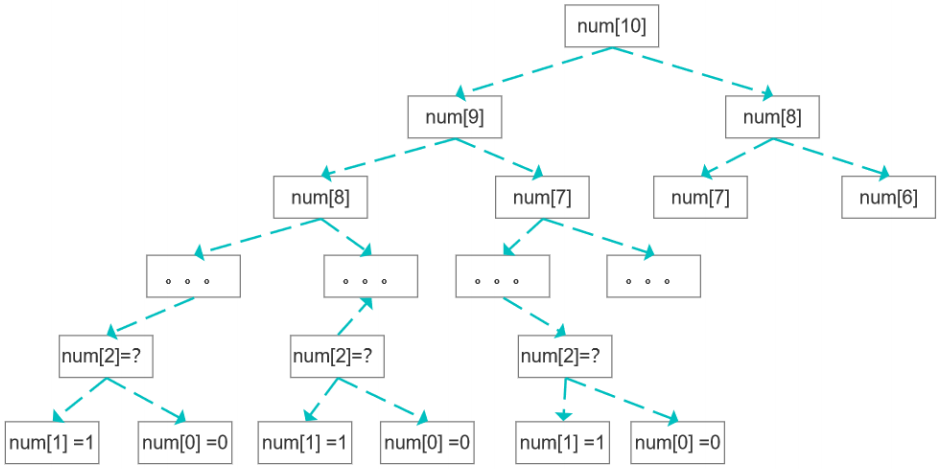

public static int calculate(int num) {
    if (num == 0) {
        return 0;
    }
    if (num == 1) {
        return 1;
    }
    return calculate(num - 1) + calculate(num - 2);
}

解法二：去重递归
递归得出具体数值之后、存储到一个集合(下标与数列下标一致)，后面递归之前先到该集合查询一次，
如果查到则无需递归、直接取值。查不到再进行递归计算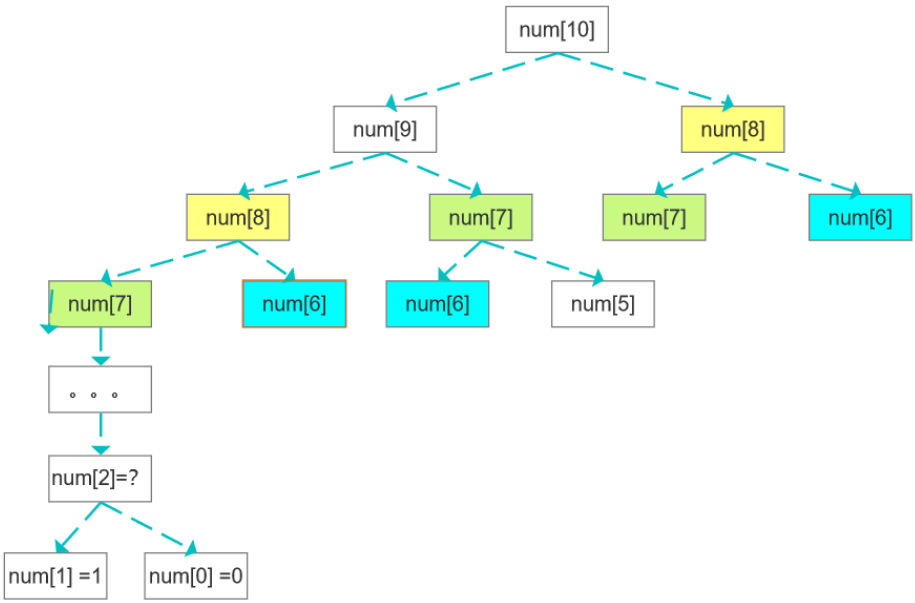

public static int calculate2(int num) {
    int[] arr = new int[num + 1];
    return recurse(arr, num);
}
private static int recurse(int[] arr, int num) {
    if (num == 0) {
        return 0;
    }
    if (num == 1) {
        return 1;
    }
    if (arr[num] != 0) {
        return arr[num];
    }
    arr[num] = recurse(arr, num - 1) + recurse(arr, num - 2);
    return arr[num];
}

解法三：双指针迭代
基于去重递归优化，集合没有必要保存每一个下标值，只需保存前两位即可，向后遍历，得出N的值

public static int iterate(int num) {
    if (num == 0) {
        return 0;
    }
    if (num == 1) {
        return 1;
    }
    int low = 0;
    int high = 1;
    for (int i = 2; i <= num; i++) {
        int sum = low + high;
        low = high;
        high = sum;
    }
    return high;
}