题目

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1

  1. 输入: s = "abcabcbb"
  2. 输出: 3  
  3. 解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2

  1. 输入: s = "bbbbb"
  2. 输出: 1
  3. 解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3

  1. 输入: s = "pwwkew"
  2. 输出: 3
  3. 解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
  4.      请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

示例 4

  1. 输入: s = ""
  2. 输出: 0

提示

  • 0 <= s.length <= 5 * 104
  • s 由英文字母、数字、符号和空格组成

思路和算法

我们先用一个例子考虑如何在较优的时间复杂度内通过本题。
我们不妨以示例一中的字符串 abcabcbb\texttt{abcabcbb}abcabcbb 为例，找出从每一个字符开始的，不包含重复字符的最长子串，那么其中最长的那个字符串即为答案。对于示例一中的字符串，我们列举出这些结果，其中括号中表示选中的字符以及最长的字符串：
以 (a)bcabcbb\texttt{(a)bcabcbb}(a)bcabcbb 开始的最长字符串为 (abc)abcbb\texttt{(abc)abcbb}(abc)abcbb；
以 a(b)cabcbb\texttt{a(b)cabcbb}a(b)cabcbb 开始的最长字符串为 a(bca)bcbb\texttt{a(bca)bcbb}a(bca)bcbb；
以 ab(c)abcbb\texttt{ab(c)abcbb}ab(c)abcbb 开始的最长字符串为 ab(cab)cbb\texttt{ab(cab)cbb}ab(cab)cbb；
以 abc(a)bcbb\texttt{abc(a)bcbb}abc(a)bcbb 开始的最长字符串为 abc(abc)bb\texttt{abc(abc)bb}abc(abc)bb；
以 abca(b)cbb\texttt{abca(b)cbb}abca(b)cbb 开始的最长字符串为 abca(bc)bb\texttt{abca(bc)bb}abca(bc)bb；
以 abcab(c)bb\texttt{abcab(c)bb}abcab(c)bb 开始的最长字符串为 abcab(cb)b\texttt{abcab(cb)b}abcab(cb)b；
以 abcabc(b)b\texttt{abcabc(b)b}abcabc(b)b 开始的最长字符串为 abcabc(b)b\texttt{abcabc(b)b}abcabc(b)b；
以 abcabcb(b)\texttt{abcabcb(b)}abcabcb(b) 开始的最长字符串为 abcabcb(b)\texttt{abcabcb(b)}abcabcb(b)。
发现了什么？如果我们依次递增地枚举子串的起始位置，那么子串的结束位置也是递增的！这里的原因在于，假设我们选择字符串中的第 k个字符作为起始位置，并且得到了不包含重复字符的最长子串的结束位置为 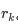image.png。那么当我们选择第 k+1 个字符作为起始位置时，首先从 k+1 到 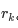image.png的字符显然是不重复的，并且由于少了原本的第 k个字符，我们可以尝试继续增大 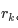image.png，直到右侧出现了重复字符为止。
这样一来，我们就可以使用「滑动窗口」来解决这个问题了：
我们使用两个指针表示字符串中的某个子串（或窗口）的左右边界，其中左指针代表着上文中「枚举子串的起始位置」，而右指针即为上文中的 rkr_krk；
在每一步的操作中，我们会将左指针向右移动一格，表示 我们开始枚举下一个字符作为起始位置，然后我们可以不断地向右移动右指针，但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后，这个子串就对应着 以左指针开始的，不包含重复字符的最长子串。我们记录下这个子串的长度；
在枚举结束后，我们找到的最长的子串的长度即为答案。
判断重复字符
在上面的流程中，我们还需要使用一种数据结构来判断 是否有重复的字符，常用的数据结构为哈希集合（即 C++ 中的 std::unordered_set，Java 中的 HashSet，Python 中的 set, JavaScript 中的 Set）。在左指针向右移动的时候，我们从哈希集合中移除一个字符，在右指针向右移动的时候，我们往哈希集合中添加一个字符。
至此，我们就完美解决了本题。

代码

  1. class Solution {
  2.     public int lengthOfLongestSubstring(String s) {
  3.         HashSet<Character> strSet = new HashSet<>();
  4.         // 字符长度
  5.         int length = s.length();
  6.         // 结果 无重复长度
  7.         int result = 0;
  8.         // 指针
  9.         int hand = -1;
  10.         for (int i = 0; i < length; ++i) {
  11.             // contains 包含
  12.             while (hand + 1 < length && !strSet.contains(s.charAt(hand + 1))) {
  13.                 if (i != 0) {
  14.                     // 每进去一趟删除一个字符
  15.                     strSet.remove(s.charAt(hand + 1));
  16.                 }
  17.                 hand++;
  18.             }
  19.             hand = -1;
  20.             // 先判断长度 再判断 集合是否不包含该字符 contains 包含
  21.             while (hand + 1 < length && !strSet.contains(s.charAt(hand + 1))) {
  22.                 // 否则添加该字符
  23.                 strSet.add(s.charAt(hand + 1));
  24.                 // 移向下一个字符
  25.                 hand++;
  26.             }
  27.             // 判断长度是否为最长
  28.             result = Math.max(result, hand - i + 1);
  29.         }
  30.         return result;
  31.     }
  32. }

复杂度分析

  • 时间复杂度：O(N)，其中 NNN 是字符串的长度。左指针和右指针分别会遍历整个字符串一次。
  • 空间复杂度：O(∣Σ∣)，其中 Σ 表示字符集（即字符串中可以出现的字符），∣Σ∣表示字符集的大小。在本题中没有明确说明字符集，因此可以默认为所有 ASCII 码在 [0,128)内的字符，即 ∣Σ∣=128。我们需要用到哈希集合来存储出现过的字符，而字符最多有 ∣Σ∣ 个，因此空间复杂度为 O(∣Σ∣)。

转载 https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/solution/wu-zhong-fu-zi-fu-de-zui-chang-zi-chuan-by-leetc-2/