Pure Python

数据预处理

data_reader

from csv import reader
def read_csv(name_of_file_to_be_read):
    dataset = list()
    with open(name_of_file_to_be_read, 'r') as file:
        every_line_of_file = reader(file)
        for line in every_line_of_file:
            if not line:
                continue
            dataset.append(line)
    return dataset
def convert_string_to_float(dataset, column):
    dataset = dataset[1:]
    for row in dataset:
        row[column] = float(row[column].strip())

rescaling

import data_reader
dataset = data_reader.read_csv('diabetes.csv')
for i in range(len(dataset[0])):
    data_reader.convert_string_to_float(dataset, i)
dataset = dataset[1:]
def find_max_and_min_in_dataset(dataset):
    max_and_min = list()
    for i in range(len(dataset[0])):
        col_values = [row[i] for row in dataset]
        value_max = max(col_values)
        value_min = min(col_values)
        max_and_min.append([value_max, value_min])
    return max_and_min
def max_min_normalization(dataset, max_and_min):
    for row in dataset:
        for i in range(len(row)):
            row[i] = (row[i] - max_and_min[i][1])/(max_and_min[i][0] - max_and_min[i][1])
def find_mean_of_dataset(dataset):
    means = list()
    for i in range(len(dataset[0])):
        col_values = [row[i] for row in dataset]
        mean = sum(col_values)/float((len(dataset)))
        means.append(mean)
    return means
def calculate_standard_deviation_of_dataset(dataset, means):
    standard_deviations = list()
    for i in range(len(dataset[0])):
        variance = [pow(row[i] - means[i], 2) for row in dataset]
        standard_deviation = pow(sum(variance)/float((len(variance)-1)), 0.5)
        standard_deviations.append(standard_deviation)
    return standard_deviations
def standardization(dataset, means, standard_deviations):
    for row in dataset:
        for i in range(len(row)):
            row[i] = (row[i] - means[i])/standard_deviations[i]
mean_list = find_mean_of_dataset(dataset)
standard_deviation_list = calculate_standard_deviation_of_dataset(dataset, mean_list)
standardization(dataset, mean_list, standard_deviation_list)
print(dataset)

train_test_split

from random import seed
from random import randrange
def train_test_split(dataset, train_proportion = 0.6):
    train_set = list()
    train_size = train_proportion * len(dataset)
    dataset_copy = list(dataset)
    while len(train_set) < train_size:
        random_choose = randrange(len(dataset_copy))
        train_set.append(dataset_copy.pop(random_choose))
    return train_set, dataset_copy

模型评估

k_fold_cross_validation

from random import seed
from random import randrange
def k_fold(dataset, k = 10):
    basket_for_splitted_data = list()
    fold_size = int(len(dataset)/k)
    dataset_copy = list(dataset)
    for i in range(k):
        choosen_fold = list()
        while len(choosen_fold) < fold_size:
            random_choose = randrange(len(dataset_copy))
            choosen_fold.append(dataset_copy.pop(random_choose))
        basket_for_splitted_data.append(choosen_fold)
    return basket_for_splitted_data
seed(888)
dataset = [[1], [2], [3], [4], [5], [6], [7], [8], [9], [10]]
k_fold_split = k_fold(dataset, 5)
print(k_fold_split)

calculate_accuracy

def calculate_accuracy_of_prediction(actual_data, predicted_data):
    correct_num = 0
    for i in range(len(actual_data)):
        if actual_data[i] == predicted_data[i]:
            correct_num += 1
    return correct_num/len(actual_data)
actual_data = [0,0,0,0,0,1,1,1,1,1]
predicted_data = [1,1,1,1,1,0,0,0,0,1]
print(calculate_accuracy_of_prediction(actual_data, predicted_data))

confusion_matrix

def confusion_matrix(actual_data, predicated_data):
    unique_calss_in_data = set(actual_data)
    matrix = [list() for x in range(len(unique_calss_in_data))]
    for i in range(len(unique_calss_in_data)):
        matrix[i] = [0 for x in range(len(unique_calss_in_data))]
    indexing_class = dict()
    for i, class_value in enumerate(unique_calss_in_data):
        indexing_class[class_value] = i
    for i in range(len(actual_data)):
        col = indexing_class[actual_data[i]]
        row = indexing_class[predicted_data[i]]
        matrix[row][col] += 1
    return unique_calss_in_data, matrix
def pretty_matrix(unique_calss_in_data, matrix):
    print('Actual     ' + ' '.join(str(x) for x in unique_calss_in_data))
    print('Predicted—-—-—-—-—-—-—-—-—-—-—-—-—-—-—-—-—-—-—-—-')
    for i, x in enumerate(unique_calss_in_data):
        print('      {}  | {}'.format(x, ' '.join(str(y) for y in matrix[i])))
actual_data = [0, 2, 0, 0, 0, 1, 1, 5, 2, 1]
predicted_data = [2, 0, 2, 0, 1, 0, 0, 0, 0, 1]
unique_calss_in_data, matrix = confusion_matrix(actual_data, predicted_data)
pretty_matrix(unique_calss_in_data, matrix)

MAE法与RMSE法

对于回归问题，最简单的检测误差方法：

平均绝对误差

def calculate_MAE(predicted_data, actual_data):
    sum_of_error = 0
    for i in range(len(predicted_data)):
        sum_of_error += abs(predicted_data[i] - actual_data[i])
    return sum_of_error/len(predicted_data)
actual_data = range(1, 11)
predicted_data = [2, 4, 3, 5, 4, 6, 5, 7, 6, 8]
calculate_MAE(predicted_data, actual_data)

均方根误差

def calculate_RMSE(predicted_data, actual_data):
    sum_of_error = 0
    for i in range(len(predicted_data)):
        sum_of_error += pow(predicted_data[i] - actual_data[i], 2)
    return pow(sum_of_error/len(predicted_data), 0.5)
actual_data = range(1, 11)
predicted_data = [2, 4, 3, 5, 4, 6, 5, 7, 6, 8]
calculate_RMSE(predicted_data, actual_data)

随机预测算法建立基准模型

Random Prediction Algorithm

def Random_Prediction_Algorithm(training_data, testing_data):
    values = [row[-1] for row in training_data] # list is unhashable
    unique_values = list(set(values))
    randomly_predicted_data = list()
    for row in testing_data:
        index = randrange(len(unique_values))
        randomly_predicted_data.append(unique_values[index])
    return randomly_predicted_data
seed(888)
training_data = [[0], [1], [2], [3], [2], [1], [0], [0], [1], [2]]
testing_data = [[None], [None], [None], [None], [None]]
predictions = Random_Prediction_Algorithm(training_data, testing_data)
print(predictions)

返回：

[0, 3, 3, 3, 3]

ZeroR Algorithm Classification

def ZeroR_Algorithm_Classification(training_data, testing_data):
    values = [row[-1] for row in training_data]
    highest_counts = max(set(values), key = values.count)
    ZeroR_Prediction = [highest_counts for i in range(len(testing_data))] # 重复最大值
    return ZeroR_Prediction
seed(888)
training_data = [[0], [1], [2], [3], [2], [1], [0], [0], [1], [2]]
testing_data = [[None], [None], [None], [None], [None]]
predictions = ZeroR_Algorithm_Classification(training_data, testing_data)
print(predictions)

返回：

[0, 0, 0, 0, 0]

ZeroR Algorithm Regression

def ZeroR_Algorithm_Regression(training_data, testing_data):
    values = [row[-1] for row in training_data]  
    prediction = sum(values)/len(values)
    ZeroR_prediction = [prediction for i in range(len(testing_data))]
    return ZeroR_prediction
seed(888)
training_data = [[1], [2],[3], [4], [5], [6], [7], [8], [9], [10]]
testing_data = [[None], [None], [None], [None], [None], [None], [None], [None], [None], [None]]
predictions = ZeroR_Algorithm_Regression(training_data, testing_data)
print(predictions)

返回：

[5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5]

Python与统计学

描述性统计与推断性统计

Descriptive stastics

1. 平均数
2. 中位数

Statistical inference

收集全量数据成本过高，所以需要以样本推断整体

sample —- sampliing —- statistic —- estimate —- hypothesis test —- > all(parameter)

Estimate:

1. Point estimation (sample size:n=100 ![](https://cdn.nlark.com/yuque/__latex/03db50bcc0d560eecac8f30a7fd08ce3.svg#card=math&code=%5Coverline%20X%20%3D%20175&height=19&width=56))
2. Confidence interval (confidence level:95% ![](https://cdn.nlark.com/yuque/__latex/79b6ffeb1d738d6772eadc5be9dfe0d5.svg#card=math&code=%5Cmu%20%3D%20%5Coverline%7BX%7D%20%5Cpm%201.96%20%5Ctimes%20S_%7B%5Coverline%20%7BX%7D%7D&height=24&width=126))
   1. ![](https://cdn.nlark.com/yuque/__latex/1ce0cdaf66b9bf4b74d1f118c30080ef.svg#card=math&code=%5Coverline%7BX%7D&height=19&width=13) 和 ![](https://cdn.nlark.com/yuque/__latex/775563ef20ecacac415f0a661f21ee48.svg#card=math&code=_%7B%5Coverline%20%7BX%7D%7D&height=13&width=11)
   2. “95%” 和 “1.96”

Hypothesis test:

1. 提出假设$H{0},H{a}$
   1. ![](https://cdn.nlark.com/yuque/__latex/7c5081abe6c2100f0e44396b6ac51661.svg#card=math&code=H_%7B0%7D&height=16&width=19) is the Hypothesis you want to reject
   2. ![](https://cdn.nlark.com/yuque/__latex/290b5855249618ae5a3d3ee809968b4b.svg#card=math&code=H_%7Ba%7D&height=16&width=19) is the Hypothesis you want to accept
   3. Example:
      1. one tail:![](https://cdn.nlark.com/yuque/__latex/981527060d01cb0dc20c1aaec8507255.svg#card=math&code=H_%7B0%7D%3A%5Cmu%20%5Cgeq%20175%2C%20H_%7Ba%7D%3A%20%5Cmu%20%3C%20175&height=16&width=172)
      2. two tails:![](https://cdn.nlark.com/yuque/__latex/fd089cde7b03129d613923707a8eb096.svg#card=math&code=H_%7B0%7D%3A%5Cmu%20%3D%20175%2C%20H_%7Ba%7D%3A%20%5Cmu%20%5Cneq%20175&height=16&width=172)
2. Calculation
   ![](https://cdn.nlark.com/yuque/__latex/389bf8cca4c3b7bd09dcf638a211d5f0.svg#card=math&code=t%20%3D%20%5Cfrac%7B%5Coverline%20%7BX%7D%20-%20175%7D%7BS_%7B%5Coverline%20X%7D%7D&height=45&width=85)
3. Draw distribution
4. What is your confidence?

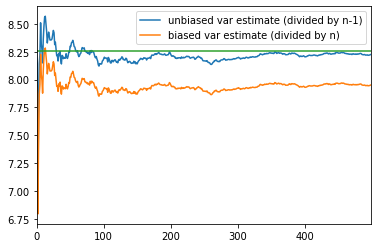
N-1与贝塞尔校正

Population Y:

1. ![](https://cdn.nlark.com/yuque/__latex/364e9abd6caee5970e6cf69c0844fd41.svg#card=math&code=Mean%28Y%29%3D%5Cmu%3D%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bi%3D1%7D%5E%7BN%7DY_%7Bi%7D&height=47&width=170)
2. 

Sample X:

随机生成10万个总体数据

%matplotlib inline
import matplotlib.pyplot as plt
from IPython.core.pylabtools import figsize
import pandas as pd
import numpy as np

np.random.seed(42)
Population = 100000
Population = pd.Series(np.random.randint(1, 11, Population))

Population.head()

0    7
1    4
2    8
3    5
4    7
dtype: int32

随机抽取500次样本

samples = {}
sample_size = 30
num_of_samples = 500
for i in range(num_of_samples):
    samples[i] = Population.sample(sample_size).reset_index(drop = True)

samples = pd.DataFrame(samples)

samples

30 rows × 500 columns

# Delta degree of freedom 
# ddof = 0, divided by n; ddof = 1, divided by n-1
biased_samples = samples.var(ddof = 0).to_frame()
biased_samples.head()

biased_samples = biased_samples.expanding().mean()
biased_samples.head()

biased_samples.columns = ['biased var estimate (divided by n)']
biased_samples.plot()

<matplotlib.axes._subplots.AxesSubplot at 0x2660c0b7b70>

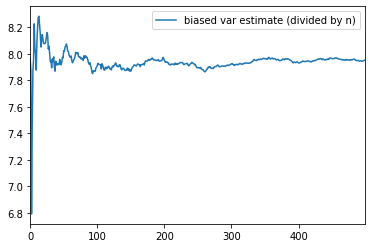
unbiased_samples = samples.var(ddof = 1).to_frame()
unbiased_samples.head()

unbiased_samples = unbiased_samples.expanding().mean()
unbiased_samples.head()

unbiased_samples.columns = ['unbiased var estimate (divided by n-1)']
unbiased_samples.plot()

<matplotlib.axes._subplots.AxesSubplot at 0x2660c3e6588>

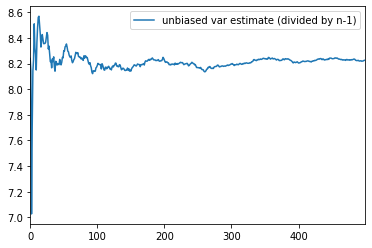
ax = unbiased_samples.plot()
biased_samples.plot(ax =ax)
real_population_variance = pd.Series(Population.var(ddof = 0), index = samples.columns)
real_population_variance.plot()

<matplotlib.axes._subplots.AxesSubplot at 0x2660c487f98>

利用假设性检验，检验相关性

T-Test：相关性是否靠谱？

第一步_立无相关性靶子

two tails test

第二步_计算T统计量

自由度
当以样本的统计量来估计总体的参数时，样本中独立或能自由变化的数据的个数

第三步_画分布，查T分布表

第四步_做判断

局限性

1. 非线性相关   
2. 异常值
3. 伪相关