1. 相关性矩阵存在的必要性
相关性矩阵,又叫做热力图,是关联图中最重要的一张图像,它能够展现多个变量两两之间的相关性
关联图的目标是探索两个事物之间关系,它展示出一个事物随着另一个事物的变化如何变化,
但之前我们描述的关联图:折线图或散点图都只能够分析两个变量之间的相关性。在实际统计学和机器学习应用当中,我们往往需要探求多个变量两两之间的相关性。

一个最典型的例子的例子是:在统计建模中,能够使用最小二乘法求解线性回归模型的充分必要条件是特征之间没有相关性(在统计学当中标准的术语叫做共线性),否则模型就会出现偏移,因此往往要先探索相关性,排除相关性,然后再建模
要探索众多变量两两之间的相关性,不太可能对每一组变量都绘制散点图,这样非常低效。
除此之外,即便绘制出了图像,也无法判断出相关性的强弱,即如果相关,究竟有多相关呢?
所以我们要选择更加有效也更加直接的方式:
1. 引入衡量相关性的数学指标:相关系数(Correlation Coefficient)
相关系数是某种类型相关性的数值度量,通常是有界的数字。最为人所知的就是皮尔逊相关系数,这个系数在-1~1之间波动,0表示完全无关,1表示完全正相关,-1表示完全负相关。
2. 绘制相关系数矩阵图,一次性查看所有变量两两之间的相关性
这张图实际上是由相关性矩阵和热力图一起构建的,热力图(heatmap)就是用颜色深浅来表示数值大小的图像
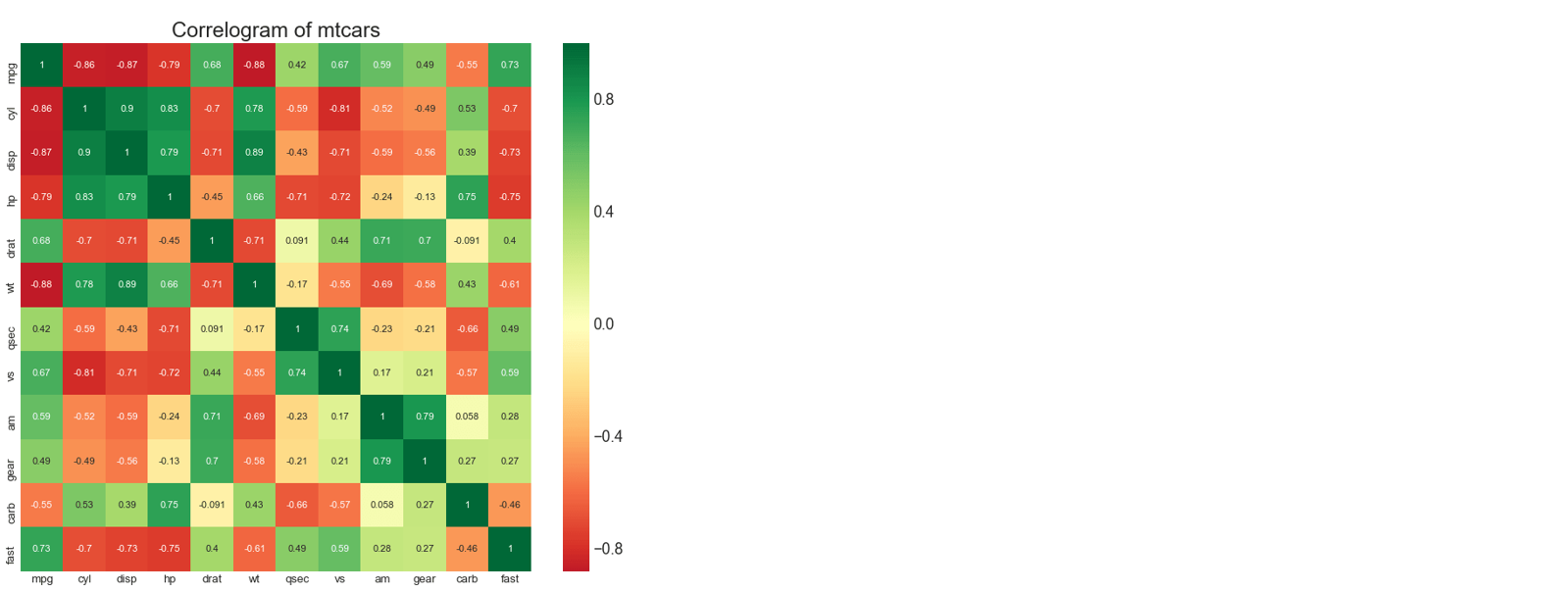 横坐标:一个数据集中的所有变量(可能包括特征或标签)
横坐标:一个数据集中的所有变量(可能包括特征或标签)
纵坐标:一个数据集中的所有变量(可能包括特征或标签)
颜色:颜色越接近红和绿,相关性越强,绿色代表正相关,红色代表负相关,浅黄色代表不相关
2. 导入需要的绘图库 & 导入数据
import numpy as npimport pandas as pdimport matplotlib as mplimport matplotlib.pyplot as pltimport seaborn as snslarge = 22; med = 16; small = 12params = {'axes.titlesize': large,'legend.fontsize': med,'figure.figsize': (16, 10),'axes.labelsize': med,'axes.titlesize': med,'xtick.labelsize': med,'ytick.labelsize': med,'figure.titlesize': large}plt.rcParams.update(params)plt.style.use('seaborn-whitegrid')sns.set_style("white")%matplotlib inline
#导入数据df = pd.read_csv("mtcars.csv")
df.head()
| mpg | cyl | disp | hp | drat | wt | qsec | vs | am | gear | carb | fast | cars | carname | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 4.582576 | 6 | 160.0 | 110 | 3.90 | 2.620 | 16.46 | 0 | 1 | 4 | 4 | 1 | Mazda RX4 | Mazda RX4 |
| 1 | 4.582576 | 6 | 160.0 | 110 | 3.90 | 2.875 | 17.02 | 0 | 1 | 4 | 4 | 1 | Mazda RX4 Wag | Mazda RX4 Wag |
| 2 | 4.774935 | 4 | 108.0 | 93 | 3.85 | 2.320 | 18.61 | 1 | 1 | 4 | 1 | 1 | Datsun 710 | Datsun 710 |
| 3 | 4.626013 | 6 | 258.0 | 110 | 3.08 | 3.215 | 19.44 | 1 | 0 | 3 | 1 | 1 | Hornet 4 Drive | Hornet 4 Drive |
| 4 | 4.324350 | 8 | 360.0 | 175 | 3.15 | 3.440 | 17.02 | 0 | 0 | 3 | 2 | 1 | Hornet Sportabout | Hornet Sportabout |
# 所用数据集mtcars记录了32种不同品牌的轿车的11个属性name = ["英里/加仑","气缸数量","排量","总马力","驱动轴比","重量","1/4英里所用时间","引擎","变速器","前进档数","化油器数量","用油是否高效","汽车","汽车名称"]df.columns = name # 替换掉英文的列名# 英里/加仑:每加仑油耗可以跑的英里数,这个数值越大代表汽车越节能# 用油是否高效:不难注意到,其实这个特征中的0和1是根据特征英里/加仑来决定的,如果英里/加仑大于4,则用油高效(1),否则用油不高效(0)# 引擎:分为V(V型)和S(直型)两种,其中1为V型,0为直型
df.head()
| 英里/加仑 | 气缸数量 | 排量 | 总马力 | 驱动轴比 | 重量 | 1/4英里所用时间 | 引擎 | 变速器 | 前进档数 | 化油器数量 | 用油是否高效 | 汽车 | 汽车名称 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 4.582576 | 6 | 160.0 | 110 | 3.90 | 2.620 | 16.46 | 0 | 1 | 4 | 4 | 1 | Mazda RX4 | Mazda RX4 |
| 1 | 4.582576 | 6 | 160.0 | 110 | 3.90 | 2.875 | 17.02 | 0 | 1 | 4 | 4 | 1 | Mazda RX4 Wag | Mazda RX4 Wag |
| 2 | 4.774935 | 4 | 108.0 | 93 | 3.85 | 2.320 | 18.61 | 1 | 1 | 4 | 1 | 1 | Datsun 710 | Datsun 710 |
| 3 | 4.626013 | 6 | 258.0 | 110 | 3.08 | 3.215 | 19.44 | 1 | 0 | 3 | 1 | 1 | Hornet 4 Drive | Hornet 4 Drive |
| 4 | 4.324350 | 8 | 360.0 | 175 | 3.15 | 3.440 | 17.02 | 0 | 0 | 3 | 2 | 1 | Hornet Sportabout | Hornet Sportabout |
(df.汽车 != df.汽车名称).sum()
0
cars 和 carname 内的数据完全一致,且由于这两列不是数值型变量,在相关性矩阵中不重要
3. 先实现相关性矩阵,再实现热力图
df.corr():实现相关性矩阵
method:填写相关系数类型的参数,可以选择”pearson”,”kendall”,”spearman”
df.corr(method = 'pearson')
| 英里/加仑 | 气缸数量 | 排量 | 总马力 | 驱动轴比 | 重量 | 1/4英里所用时间 | 引擎 | 变速器 | 前进档数 | 化油器数量 | 用油是否高效 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 英里/加仑 | 1.000000 | -0.858539 | -0.867536 | -0.787309 | 0.680312 | -0.883453 | 0.420317 | 0.669260 | 0.593153 | 0.487226 | -0.553703 | 0.730748 |
| 气缸数量 | -0.858539 | 1.000000 | 0.902033 | 0.832447 | -0.699938 | 0.782496 | -0.591242 | -0.810812 | -0.522607 | -0.492687 | 0.526988 | -0.695182 |
| 排量 | -0.867536 | 0.902033 | 1.000000 | 0.790949 | -0.710214 | 0.887980 | -0.433698 | -0.710416 | -0.591227 | -0.555569 | 0.394977 | -0.732073 |
| 总马力 | -0.787309 | 0.832447 | 0.790949 | 1.000000 | -0.448759 | 0.658748 | -0.708223 | -0.723097 | -0.243204 | -0.125704 | 0.749812 | -0.751422 |
| 驱动轴比 | 0.680312 | -0.699938 | -0.710214 | -0.448759 | 1.000000 | -0.712441 | 0.091205 | 0.440278 | 0.712711 | 0.699610 | -0.090790 | 0.400430 |
| 重量 | -0.883453 | 0.782496 | 0.887980 | 0.658748 | -0.712441 | 1.000000 | -0.174716 | -0.554916 | -0.692495 | -0.583287 | 0.427606 | -0.611265 |
| 1/4英里所用时间 | 0.420317 | -0.591242 | -0.433698 | -0.708223 | 0.091205 | -0.174716 | 1.000000 | 0.744535 | -0.229861 | -0.212682 | -0.656249 | 0.488649 |
| 引擎 | 0.669260 | -0.810812 | -0.710416 | -0.723097 | 0.440278 | -0.554916 | 0.744535 | 1.000000 | 0.168345 | 0.206023 | -0.569607 | 0.594588 |
| 变速器 | 0.593153 | -0.522607 | -0.591227 | -0.243204 | 0.712711 | -0.692495 | -0.229861 | 0.168345 | 1.000000 | 0.794059 | 0.057534 | 0.283129 |
| 前进档数 | 0.487226 | -0.492687 | -0.555569 | -0.125704 | 0.699610 | -0.583287 | -0.212682 | 0.206023 | 0.794059 | 1.000000 | 0.274073 | 0.266919 |
| 化油器数量 | -0.553703 | 0.526988 | 0.394977 | 0.749812 | -0.090790 | 0.427606 | -0.656249 | -0.569607 | 0.057534 | 0.274073 | 1.000000 | -0.461196 |
| 用油是否高效 | 0.730748 | -0.695182 | -0.732073 | -0.751422 | 0.400430 | -0.611265 | 0.488649 | 0.594588 | 0.283129 | 0.266919 | -0.461196 | 1.000000 |
df.corr(method = 'spearman')
| 英里/加仑 | 气缸数量 | 排量 | 总马力 | 驱动轴比 | 重量 | 1/4英里所用时间 | 引擎 | 变速器 | 前进档数 | 化油器数量 | 用油是否高效 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 英里/加仑 | 1.000000 | -0.910801 | -0.908882 | -0.894665 | 0.651455 | -0.886422 | 0.466936 | 0.706597 | 0.562006 | 0.542782 | -0.657498 | 0.803735 |
| 气缸数量 | -0.910801 | 1.000000 | 0.927652 | 0.901791 | -0.678881 | 0.857728 | -0.572351 | -0.813789 | -0.522071 | -0.564310 | 0.580068 | -0.706188 |
| 排量 | -0.908882 | 0.927652 | 1.000000 | 0.851043 | -0.683592 | 0.897706 | -0.459782 | -0.723664 | -0.624068 | -0.594470 | 0.539778 | -0.697788 |
| 总马力 | -0.894665 | 0.901791 | 0.851043 | 1.000000 | -0.520125 | 0.774677 | -0.666606 | -0.751593 | -0.362328 | -0.331402 | 0.733379 | -0.723960 |
| 驱动轴比 | 0.651455 | -0.678881 | -0.683592 | -0.520125 | 1.000000 | -0.750390 | 0.091869 | 0.447457 | 0.686571 | 0.744816 | -0.125223 | 0.391159 |
| 重量 | -0.886422 | 0.857728 | 0.897706 | 0.774677 | -0.750390 | 1.000000 | -0.225401 | -0.587016 | -0.737713 | -0.676128 | 0.499812 | -0.591733 |
| 1/4英里所用时间 | 0.466936 | -0.572351 | -0.459782 | -0.666606 | 0.091869 | -0.225401 | 1.000000 | 0.791571 | -0.203332 | -0.148200 | -0.658718 | 0.467413 |
| 引擎 | 0.706597 | -0.813789 | -0.723664 | -0.751593 | 0.447457 | -0.587016 | 0.791571 | 1.000000 | 0.168345 | 0.282662 | -0.633695 | 0.594588 |
| 变速器 | 0.562006 | -0.522071 | -0.624068 | -0.362328 | 0.686571 | -0.737713 | -0.203332 | 0.168345 | 1.000000 | 0.807688 | -0.064365 | 0.283129 |
| 前进档数 | 0.542782 | -0.564310 | -0.594470 | -0.331402 | 0.744816 | -0.676128 | -0.148200 | 0.282662 | 0.807688 | 1.000000 | 0.114887 | 0.326405 |
| 化油器数量 | -0.657498 | 0.580068 | 0.539778 | 0.733379 | -0.125223 | 0.499812 | -0.658718 | -0.633695 | -0.064365 | 0.114887 | 1.000000 | -0.484982 |
| 用油是否高效 | 0.803735 | -0.706188 | -0.697788 | -0.723960 | 0.391159 | -0.591733 | 0.467413 | 0.594588 | 0.283129 | 0.326405 | -0.484982 | 1.000000 |
df.corr(method = 'kendall')
| 英里/加仑 | 气缸数量 | 排量 | 总马力 | 驱动轴比 | 重量 | 1/4英里所用时间 | 引擎 | 变速器 | 前进档数 | 化油器数量 | 用油是否高效 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 英里/加仑 | 1.000000 | -0.795313 | -0.768131 | -0.742813 | 0.464549 | -0.727832 | 0.315365 | 0.589679 | 0.469013 | 0.433151 | -0.504395 | 0.670744 |
| 气缸数量 | -0.795313 | 1.000000 | 0.814426 | 0.785186 | -0.551318 | 0.728261 | -0.448970 | -0.771001 | -0.494621 | -0.512543 | 0.465430 | -0.669057 |
| 排量 | -0.768131 | 0.814426 | 1.000000 | 0.665999 | -0.498983 | 0.743382 | -0.300815 | -0.603306 | -0.520274 | -0.475980 | 0.413736 | -0.581733 |
| 总马力 | -0.742813 | 0.785186 | 0.665999 | 1.000000 | -0.382627 | 0.611308 | -0.472906 | -0.630593 | -0.303996 | -0.279446 | 0.595984 | -0.607408 |
| 驱动轴比 | 0.464549 | -0.551318 | -0.498983 | -0.382627 | 1.000000 | -0.547150 | 0.032722 | 0.375101 | 0.575548 | 0.583925 | -0.095352 | 0.327906 |
| 重量 | -0.727832 | 0.728261 | 0.743382 | 0.611308 | -0.547150 | 1.000000 | -0.141988 | -0.488479 | -0.613879 | -0.543596 | 0.371374 | -0.492403 |
| 1/4英里所用时间 | 0.315365 | -0.448970 | -0.300815 | -0.472906 | 0.032722 | -0.141988 | 1.000000 | 0.657543 | -0.168904 | -0.091261 | -0.506439 | 0.388271 |
| 引擎 | 0.589679 | -0.771001 | -0.603306 | -0.630593 | 0.375101 | -0.488479 | 0.657543 | 1.000000 | 0.168345 | 0.269748 | -0.576927 | 0.594588 |
| 变速器 | 0.469013 | -0.494621 | -0.520274 | -0.303996 | 0.575548 | -0.613879 | -0.168904 | 0.168345 | 1.000000 | 0.770788 | -0.058599 | 0.283129 |
| 前进档数 | 0.433151 | -0.512543 | -0.475980 | -0.279446 | 0.583925 | -0.543596 | -0.091261 | 0.269748 | 0.770788 | 1.000000 | 0.098015 | 0.311492 |
| 化油器数量 | -0.504395 | 0.465430 | 0.413736 | 0.595984 | -0.095352 | 0.371374 | -0.506439 | -0.576927 | -0.058599 | 0.098015 | 1.000000 | -0.441537 |
| 用油是否高效 | 0.670744 | -0.669057 | -0.581733 | -0.607408 | 0.327906 | -0.492403 | 0.388271 | 0.594588 | 0.283129 | 0.311492 | -0.441537 | 1.000000 |
什么时候用什么相关系数?变量相关时:
| 分类型变量vs分类型变量 | 分类型变量vs连续型变量 | 连续型变量vs连续型变量 |
|---|---|---|
| 列联表分析 卡方检验(chi-squared) |
二分类:点双列相关(皮尔逊相关系数的一种特殊情况) 多分类:Kruskal-Wallis H检验(如t检验或方差分析) |
线性相关:皮尔逊相关系数 非线性相关:以斯皮尔曼相关系数为代表的一系列等级相关系数 |
比较特别的是kendall这个相关系数,它对比的是两个变量按数量排序时(从小到大,或者从大到小),数据排序的相似性。
其他相关系数,可以在scipy,numpy库中找到
coef = df.corr()
sns.heatmap:把相关性矩阵放到热力图里去
data:输入的相关性矩阵
cmap:使用的光谱(热力图需要渐变光谱,而不是随机的一组颜色)
center:绘制有色数据时,位于光谱中心的颜色所对应的值,注意:这是一个控制颜色的参数。如果没有指定cmap,使用此参数将更改默认的cmap参数。我们一般在center中填写数据的中值,比如皮尔逊相关系数的取值范围是[-1,1],我们就在center中填写0
annot:如果为True,则在热力图的每个单元格中写入数据值。如果是一个类似于data形状的数组,那么使用它来注释热图而不是原始数据
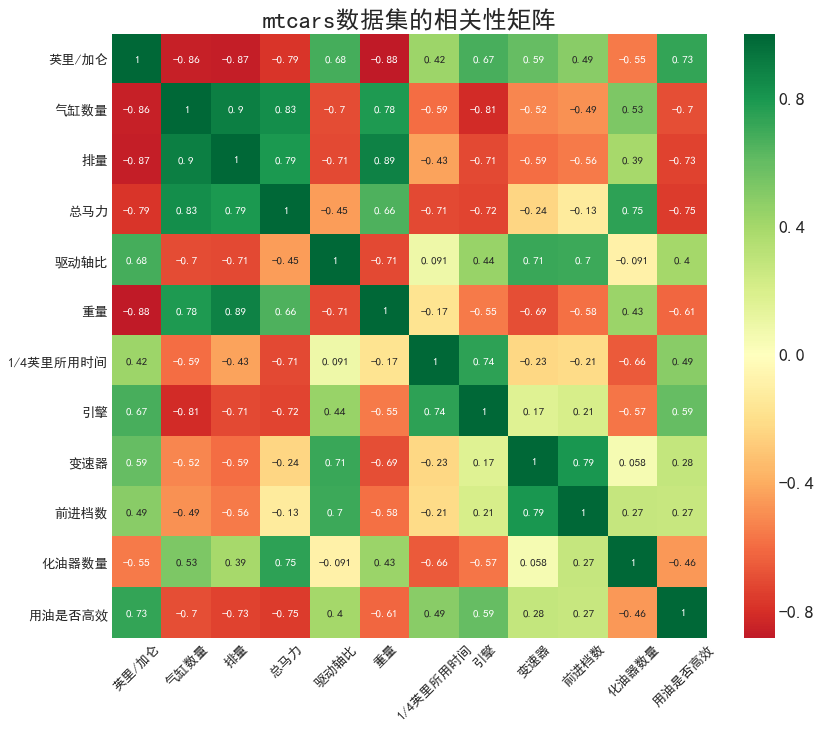
# 确保正常显示中文+负号plt.rcParams['font.sans-serif']=['SimHei']plt.rcParams['axes.unicode_minus']=False# 绘制图像plt.figure(figsize = (12, 10), dpi = 80)sns.heatmap(coef# , xticklabels = coef.columns # 横坐标标签,此时可不输入# , yticklabels = coef.columns # 纵坐标标签,此时可不输入, cmap = 'RdYlGn', center = 0 # 控制颜色,而不是控制取值范围, annot = True)# 装饰图像plt.title('mtcars数据集的相关性矩阵', fontsize = 22)plt.xticks(fontsize = 12, rotation = 45 # 文字旋转, horizontalalignment = 'center' # 刻度的相对位置)plt.yticks(fontsize = 12)
(array([ 0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5, 10.5,11.5]), <a list of 12 Text yticklabel objects>)
4. 解读图像
如果人们对家用车最关心的方面是油耗,那买车时该参考哪些属性?
找到和“英里/加仑”这个指标正相关的属性:
- 驱动轴比 0.68
- 1/4英里所用时间 0.42
- 引擎 0.67
- 变速器 0.59
- 前进档数 0.49
- 用油是否高效 0.73 (这个属性由“英里/加仑”计算得出,参考意义不大)
找到和“英里/加仑”这个指标负相关的属性:
- 气缸数量 0.86
- 排量 0.87
- 总马力 0.79
- 重量 0.88
- 化油器数量 0.55
人们为什么购买大排量汽车?
找到和“排量”这个指标正相关的属性:
- 总马力 0.79
- 气缸数量 0.9
- 重量 0.89
- 化油器数量 0.39
找到和“排量”这个指标负相关的属性:
- 英里/加仑 0.87
- 1/4英里所用时间 0.43
- 引擎 0.71
- 变速器 0.59
- 前进档数 0.56
- 驱动轴比 0.71
- 用油是否高效 0.73
由上可知,人们为了追求更强的马力、加速更快才购买大排量汽车。那么还有哪些因素影响汽车的马力?
或者说,马力更强的车有哪些特征?
5. 相关性矩阵图在统计学中的应用
删除相关性高的特征
如果一个特征,对其他每一特征都有较高的相关性,那么就可以删除掉这个特征,如
英里/加仑
气缸数量
排量
如果一个特征,与某一特征的相关性很小,那么就可以保留这个特征,如
总马力

