一、 逻辑回归概述

  1. from sklearn.linear_model import LogisticRegression as LR
  2. from sklearn.datasets import load_breast_cancer
  3. import numpy as np
  4. import pandas as pd
  5. import matplotlib.pyplot as plt
  6. %matplotlib inline
  8. from sklearn.model_selection import train_test_split
  9. from sklearn.metrics import accuracy_score
  10. from sklearn.model_selection import cross_val_score
  11. from sklearn.feature_selection import SelectFromModel
  1. data = load_breast_cancer() # 实例化，得到一个字典
  2. x = data.data
  3. y = data.target
  5. x.shape
  1. (569, 30)
  1. lrl1 = LR(penalty = 'l1', solver = 'liblinear', C = 0.5, max_iter = 1000)
  2. lrl2 = LR(penalty = 'l2', solver = 'liblinear', C = 0.5, max_iter = 1000)
  1. lrl1 = lrl1.fit(x, y)
  2. lrl1.coef_
  1. array([[ 3.99870273,  0.03177392, -0.13689412, -0.01621641,  0.        ,
  2.          0.        ,  0.        ,  0.        ,  0.        ,  0.        ,
  3.          0.        ,  0.50497324,  0.        , -0.07127604,  0.        ,
  4.          0.        ,  0.        ,  0.        ,  0.        ,  0.        ,
  5.          0.        , -0.24570638, -0.12849964, -0.01441515,  0.        ,
  6.          0.        , -2.04390881,  0.        ,  0.        ,  0.        ]])
  1. (lrl1.coef_ != 0).sum(axis = 1)
  1. array([10])
  1. lrl2 = lrl2.fit(x, y)
  2. lrl2.coef_
  1. array([[ 1.61543234e+00,  1.02284415e-01,  4.78483684e-02,
  2.         -4.43927107e-03, -9.42247882e-02, -3.01420673e-01,
  3.         -4.56065677e-01, -2.22346063e-01, -1.35660484e-01,
  4.         -1.93917198e-02,  1.61646580e-02,  8.84531037e-01,
  5.          1.20301273e-01, -9.47422278e-02, -9.81687769e-03,
  6.         -2.37399092e-02, -5.71846204e-02, -2.70190106e-02,
  7.         -2.77563737e-02,  1.98122260e-04,  1.26394730e+00,
  8.         -3.01762592e-01, -1.72784162e-01, -2.21786411e-02,
  9.         -1.73339657e-01, -8.79070550e-01, -1.16325561e+00,
  10.         -4.27661014e-01, -4.20612369e-01, -8.69820058e-02]])

L1正则化本质上是一种特征选择
L2正则化在加强的过程中，会尽量让每一个特征都对模型有贡献

  1. l1 = []
  2. l2 = []
  3. l1test = []
  4. l2test = []
  6. Xtrain, Xtest, Ytrain, Ytest = train_test_split(x, y, test_size = 0.3, random_state = 420)
  8. for i in np.linspace(0.05, 1, 19):
  9.     lrl1 = LR(C = i, penalty = 'l1', solver = 'liblinear', max_iter = 1000)
  10.     lrl2 = LR(C = i, penalty = 'l2', solver = 'liblinear', max_iter = 1000)
  11.     lrl1.fit(Xtrain, Ytrain)
  12.     lrl2.fit(Xtrain, Ytrain)
  14.     l1.append(accuracy_score(lrl1.predict(Xtrain), Ytrain))
  15.     l1test.append(accuracy_score(lrl1.predict(Xtest), Ytest))
  17.     l2.append(accuracy_score(lrl2.predict(Xtrain), Ytrain))
  18.     l2test.append(accuracy_score(lrl2.predict(Xtest), Ytest))
  20. plt.figure(figsize  = (6, 6))
  22. graph = [l1, l2, l1test, l2test]
  23. color = ['green', 'black', 'lightgreen', 'gray']
  24. label = ['L1', 'L2', 'L1test', 'L2test']
  26. for i in range(len(graph)):
  27.     plt.plot(np.linspace(0.05, 1, 19), graph[i], color = color[i], label = label[i])
  29. plt.legend()
  1. <matplotlib.legend.Legend at 0x1eb56390278>

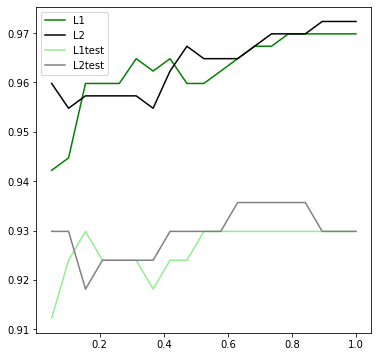
output_8_1.png

逻辑回归在训练时的目标是，提高训练集的预测准确率。所以这里监控训练集的准确率。

二、 逻辑回归的特征工程

  • 业务选择
  • PCA 和 SVD
  • 统计方法
  • 嵌入法 Embedded
  1. LR_ = LR(solver = 'liblinear', C = 0.8, random_state = 420)
  2. cross_val_score(LR_, x, y, cv = 10).mean()
  1. 0.9508145363408522
  1. x_embedded = SelectFromModel(LR_, 
  2.                              norm_order = 1 # 使用L1范式筛选，模型会去掉所有在L1范式下被判断为无效的特征
  3.                             ).fit_transform(x, y)
  4. x_embedded.shape
  1. (569, 9)
  1. x.shape
  1. (569, 30)
  1. cross_val_score(LR_, x_embedded, y).mean()
  1. 0.9349945660611707

进一步提升模型的拟合效果

1. 调节threshold

根据特征重要性选择特征
在逻辑回归中，特征重要性就是系数，此时特征选择的判断指标就不是L1范数，而是属性coef_，即特征的参数

  1. abs(LR_.fit(x, y).coef_).max()
  1. 1.9407192479360273
  1. LR_.fit(x, y).coef_
  1. array([[ 1.94071925,  0.11027501, -0.02792478, -0.00347267, -0.13418458,
  2.         -0.36887791, -0.58229351, -0.30118379, -0.19522369, -0.02391175,
  3.         -0.01172073,  1.12398531,  0.04214842, -0.0940855 , -0.01457835,
  4.         -0.00486005, -0.05146662, -0.03584081, -0.03757288,  0.0042326 ,
  5.          1.24863871, -0.32757391, -0.13662037, -0.0236736 , -0.24820117,
  6.         -1.05186104, -1.44596614, -0.57989786, -0.6022902 , -0.10544953]])

系数越大，该系数对应的特征对逻辑回归贡献越大

  1. fullx = []
  2. fsx = []
  4. threshold = np.linspace(0, abs(LR_.fit(x, y).coef_).max(), 20)
  6. k = 0
  7. for i in threshold:
  8.     x_embedded = SelectFromModel(LR_, threshold = i).fit_transform(x, y)
  9.     fullx.append(cross_val_score(LR_, x, y, cv = 5).mean())
  10.     fsx.append(cross_val_score(LR_, x_embedded, y, cv = 5).mean())
  11.     print(threshold[k], x_embedded.shape[1])
  12.     k += 1
  14. plt.figure(figsize = (20, 5))
  15. plt.plot(threshold, fullx, label = 'full')
  16. plt.plot(threshold, fsx, label = 'feature selection')
  17. plt.xticks(threshold)
  18. plt.legend()
  1. 0.0 30
  2. 0.1021431183124225 17
  3. 0.204286236624845 12
  4. 0.3064293549372675 10
  5. 0.40857247324969 8
  6. 0.5107155915621124 8
  7. 0.612858709874535 5
  8. 0.7150018281869575 5
  9. 0.81714494649938 5
  10. 0.9192880648118025 5
  11. 1.0214311831242249 5
  12. 1.1235743014366475 4
  13. 1.22571741974907 3
  14. 1.3278605380614925 2
  15. 1.430003656373915 2
  16. 1.5321467746863375 1
  17. 1.63428989299876 1
  18. 1.7364330113111823 1
  19. 1.838576129623605 1
  20. 1.9407192479360273 1
  26. <matplotlib.legend.Legend at 0x1eb56460780>

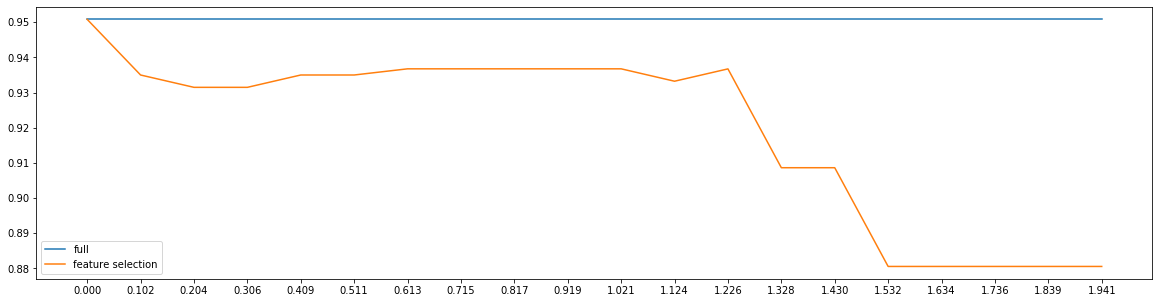
output_24_2.png

细化学习曲线
  1. fullx = []
  2. fsx = []
  4. threshold = np.linspace(0, 0.1021431183124225, 20)
  6. k = 0
  7. for i in threshold:
  8.     x_embedded = SelectFromModel(LR_, threshold = i).fit_transform(x, y)
  9.     fullx.append(cross_val_score(LR_, x, y, cv = 5).mean())
  10.     fsx.append(cross_val_score(LR_, x_embedded, y, cv = 5).mean())
  11.     print(threshold[k], x_embedded.shape[1])
  12.     k += 1
  14. plt.figure(figsize = (20, 5))
  15. plt.plot(threshold, fullx, label = 'full')
  16. plt.plot(threshold, fsx, label = 'feature selection')
  17. plt.xticks(threshold)
  18. plt.legend()
  1. 0.0 30
  2. 0.005375953595390658 27
  3. 0.010751907190781316 27
  4. 0.016127860786171976 25
  5. 0.021503814381562632 25
  6. 0.026879767976953288 23
  7. 0.03225572157234395 22
  8. 0.03763167516773461 20
  9. 0.043007628763125264 19
  10. 0.04838358235851592 19
  11. 0.053759535953906576 18
  12. 0.05913548954929724 18
  13. 0.0645114431446879 18
  14. 0.06988739674007856 18
  15. 0.07526335033546921 18
  16. 0.08063930393085987 18
  17. 0.08601525752625053 18
  18. 0.09139121112164118 18
  19. 0.09676716471703184 17
  20. 0.1021431183124225 17
  26. <matplotlib.legend.Legend at 0x1eb566f7c88>

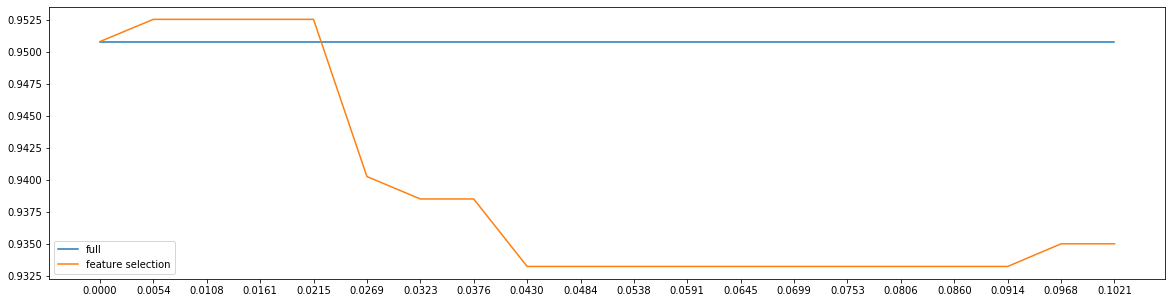
output_26_2.png

要想保持较高的准确率，仍需25个特征。因此调节threshold属于无效的方法。

2. 调节逻辑回归的类LR

使用L1范数，通过画C的学习曲线来实现

  1. fullx = []
  2. fsx = []
  4. C = np.arange(0.01, 10.01, 0.5)
  6. for i in C:
  7.     LR_ = LR(solver = 'liblinear', C = i, random_state = 420) # 因为时调节模型本身，所以每次循环都需要重新建模
  8.     x_embedded = SelectFromModel(LR_, norm_order = 1).fit_transform(x, y)
  10.     fullx.append(cross_val_score(LR_, x, y, cv = 10).mean())
  11.     fsx.append(cross_val_score(LR_, x_embedded, y, cv = 10).mean())
  13. print(max(fsx), C[fsx.index(max(fsx))])
  15. plt.figure(figsize = (20, 5))
  16. plt.plot(C, fullx, label = 'full')
  17. plt.plot(C, fsx, label = 'feature selection')
  18. plt.xticks(C)
  19. plt.legend()
  1. 0.9561090225563911 7.01
  7. <matplotlib.legend.Legend at 0x1eb56890f28>

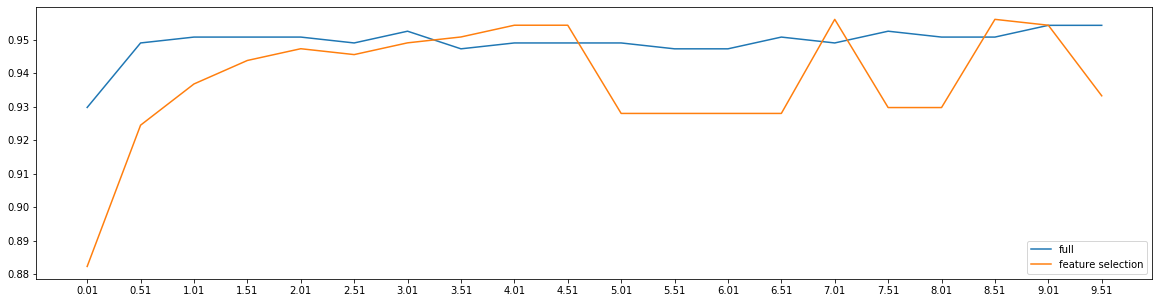
output_29_2.png

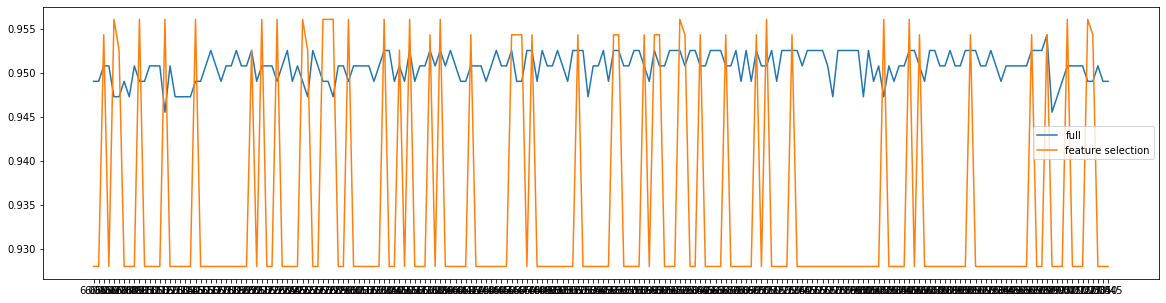
特征选择后，模型效果波动较大，数次好于特征选择前的模型效果

细化学习曲线
  1. fullx = []
  2. fsx = []
  4. C = np.arange(6.05, 7.05, 0.005)
  6. for i in C:
  7.     LR_ = LR(solver = 'liblinear', C = i, random_state = 420) # 因为时调节模型本身，所以每次循环都需要重新建模
  8.     x_embedded = SelectFromModel(LR_, norm_order = 1).fit_transform(x, y)
  10.     fullx.append(cross_val_score(LR_, x, y, cv = 10).mean())
  11.     fsx.append(cross_val_score(LR_, x_embedded, y, cv = 10).mean())
  13. print(max(fsx), C[fsx.index(max(fsx))])
  15. plt.figure(figsize = (20, 5))
  16. plt.plot(C, fullx, label = 'full')
  17. plt.plot(C, fsx, label = 'feature selection')
  18. plt.xticks(C)
  19. plt.legend()
  1. 0.9561090225563911 6.069999999999999
  7. <matplotlib.legend.Legend at 0x1eb56b13978>

output_32_2.png

  1. LR_ = LR(solver = 'liblinear', C = 6.069999999999999, random_state = 420)
  2. cross_val_score(LR_, x, y, cv = 10).mean()
  1. 0.9473057644110275
  1. LR_ = LR(solver = 'liblinear', C = 6.069999999999999, random_state = 420)
  2. x_embedded = SelectFromModel(LR_, norm_order = 1).fit_transform(x, y)
  3. cross_val_score(LR_, x_embedded, y, cv = 10).mean()
  1. 0.9561090225563911
  1. x_embedded.shape
  1. (569, 11)
  • 系数累加法
  • 包装法

三、 重要参数及概念

参数

max_iter multi_class ovr: one-vs-rest 表示分类问题是二分类，或让模型使用“一对多”的形式来处理问。0.21版本的默认值

multinomial: many-vs-many 表示处理多分类问题。这种输入在参数solve是’liblinear’时不可用

auto 根据数据的分类情况和其他参数，来确定模型要处理的分类问题的类型 如果数据是二分类，或solver取值为’liblinear’，’auto’默认选择’ovr’ 反之，则会选择’multinomial’

solver

  1. liblinear：坐标下降法，二分类和ovr专用
  2. lbfgs
  3. newton-cg
  4. sag：随机平均梯度下降，与普通梯度下降法的区别是每次迭代仅用一部分的样本来计算梯度
  5. saga：随机平均梯度下降，用来处理稀疏多项逻辑回归

class_weight

概念

梯度

逻辑回归和信用评分卡 - 图6> 逻辑回归和信用评分卡 - 图7

步长 逻辑回归和信用评分卡 - 图8 步长不是任何物理距离，它甚至不是梯度下降过程中任何距离的直接变化，它是梯度向量的大小d上的一个比例，影响着参数向量逻辑回归和信用评分卡 - 图9每次迭代后改变的部分

样本不均衡

  1. 标签的一类天然占有很大的比例
  2. 误分类的代价很高

以上两种状况下，我们希望准确捕获少数类，甚至不惜误判多数类 给占比小的标签更多的权重，让模型往偏向少数类的方向建模

解决方法

  1. 调节参数class_weight
  2. 采样法

上采样：增加少数类的样本 下采样：减少多数类的样本

  1. l2 = []
  3. Xtrain, Xtest, Ytrain, Ytest = train_test_split(x, y)
  4. for i in range(1, 201, 10):
  5.     lrl2 = LR(penalty = 'l2', solver = 'liblinear', C = 0.8, max_iter = i)
  6.     lrl2.fit(Xtrain,  Ytrain)
  7.     l2.append(cross_val_score(lrl2, x, y).mean())
  9. plt.figure(figsize = (20, 5))
  10. plt.plot(range(1, 201, 10), l2, 'black')
  11. plt.xticks(range(1, 201, 10));
  1. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  2.   "the number of iterations.", ConvergenceWarning)
  3. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  4.   "the number of iterations.", ConvergenceWarning)
  5. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  6.   "the number of iterations.", ConvergenceWarning)
  7. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  8.   "the number of iterations.", ConvergenceWarning)
  9. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  10.   "the number of iterations.", ConvergenceWarning)
  11. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  12.   "the number of iterations.", ConvergenceWarning)
  13. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  14.   "the number of iterations.", ConvergenceWarning)
  15. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  16.   "the number of iterations.", ConvergenceWarning)
  17. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  18.   "the number of iterations.", ConvergenceWarning)
  19. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  20.   "the number of iterations.", ConvergenceWarning)
  21. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  22.   "the number of iterations.", ConvergenceWarning)
  23. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  24.   "the number of iterations.", ConvergenceWarning)
  25. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  26.   "the number of iterations.", ConvergenceWarning)
  27. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  28.   "the number of iterations.", ConvergenceWarning)
  29. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  30.   "the number of iterations.", ConvergenceWarning)
  31. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  32.   "the number of iterations.", ConvergenceWarning)
  33. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  34.   "the number of iterations.", ConvergenceWarning)

output_40_1.png

  1. l2 = []
  2. l2test = []
  4. Xtrain, Xtest, Ytrain, Ytest = train_test_split(x, y, test_size = 0.3, random_state = 420)
  5. for i in range(1, 201, 10):
  6.     lrl2 = LR(penalty = 'l2', solver = 'liblinear', C = 0.8, max_iter = i)
  7.     lrl2.fit(Xtrain,  Ytrain)
  8.     l2.append(accuracy_score(lrl2.predict(Xtrain), Ytrain))
  9.     l2test.append(accuracy_score(lrl2.predict(Xtest), Ytest))
  11. graph = [l2, l2test]
  12. label = ['l2', 'l2test']
  13. color = ['black', 'gray']
  15. plt.figure(figsize = (20, 5))
  16. for i in range(len(graph)):
  17.     plt.plot(range(1, 201, 10), graph[i], color = color[i], label = label[i])
  18. plt.legend()
  19. plt.xticks(range(1, 201, 10));
  1. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  2.   "the number of iterations.", ConvergenceWarning)
  3. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  4.   "the number of iterations.", ConvergenceWarning)
  5. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  6.   "the number of iterations.", ConvergenceWarning)

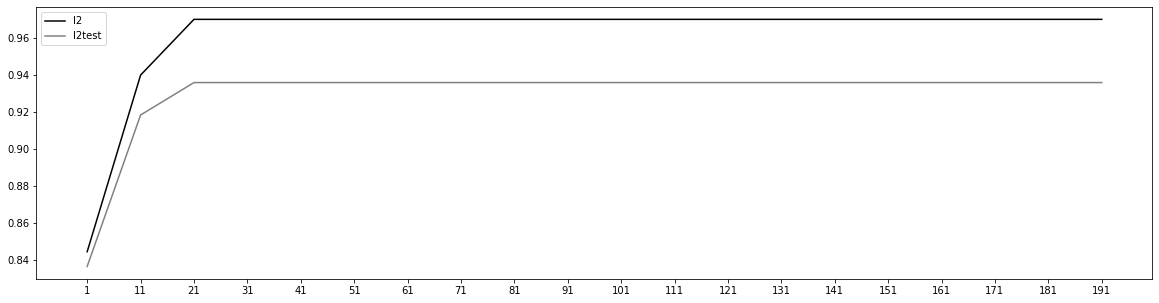
output_41_1.png

  1. lrl2.n_iter_
  1. array([24], dtype=int32)
  1. from sklearn.datasets import load_iris
  2. iris = load_iris()
  1. set(iris.target)
  1. {0, 1, 2}
  1. for multi_class in ('multinomial', 'ovr'):
  2.     lr = LR(solver = 'sag', max_iter = 100, random_state = 42, 
  3.             multi_class = multi_class).fit(iris.data, iris.target)
  5.     print('training score: %.3f (%s)' % (lr.score(iris.data, iris.target), multi_class))
  1. training score: 0.987 (multinomial)
  2. training score: 0.960 (ovr)
  5. C:\anaconda\lib\site-packages\sklearn\linear_model\_sag.py:330: ConvergenceWarning: The max_iter was reached which means the coef_ did not converge
  6.   "the coef_ did not converge", ConvergenceWarning)
  7. C:\anaconda\lib\site-packages\sklearn\linear_model\_sag.py:330: ConvergenceWarning: The max_iter was reached which means the coef_ did not converge
  8.   "the coef_ did not converge", ConvergenceWarning)
  9. C:\anaconda\lib\site-packages\sklearn\linear_model\_sag.py:330: ConvergenceWarning: The max_iter was reached which means the coef_ did not converge
  10.   "the coef_ did not converge", ConvergenceWarning)
  11. C:\anaconda\lib\site-packages\sklearn\linear_model\_sag.py:330: ConvergenceWarning: The max_iter was reached which means the coef_ did not converge
  12.   "the coef_ did not converge", ConvergenceWarning)
  1. y_predict = lr.predict(iris.data)
  2. y_predict
  1. array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  2.        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  3.        0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
  4.        2, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1,
  5.        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  6.        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
  7.        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
  1. (y_predict == iris.target).sum()/len(iris.target)
  1. 0.96

四、 案例：评分卡

数据预处理

  1. data = pd.read_csv('rankingcard.csv', index_col = 0)
  1. data.head()
SeriousDlqin2yrs RevolvingUtilizationOfUnsecuredLines age NumberOfTime30-59DaysPastDueNotWorse DebtRatio MonthlyIncome NumberOfOpenCreditLinesAndLoans NumberOfTimes90DaysLate NumberRealEstateLoansOrLines NumberOfTime60-89DaysPastDueNotWorse NumberOfDependents
1 1 0.766127 45 2 0.802982 9120.0 13 0 6 0 2.0
2 0 0.957151 40 0 0.121876 2600.0 4 0 0 0 1.0
3 0 0.658180 38 1 0.085113 3042.0 2 1 0 0 0.0
4 0 0.233810 30 0 0.036050 3300.0 5 0 0 0 0.0
5 0 0.907239 49 1 0.024926 63588.0 7 0 1 0 0.0 
  1. data.shape
  1. (150000, 11)
  1. data.info()
  1. <class 'pandas.core.frame.DataFrame'>
  2. Int64Index: 150000 entries, 1 to 150000
  3. Data columns (total 11 columns):
  4. SeriousDlqin2yrs                        150000 non-null int64
  5. RevolvingUtilizationOfUnsecuredLines    150000 non-null float64
  6. age                                     150000 non-null int64
  7. NumberOfTime30-59DaysPastDueNotWorse    150000 non-null int64
  8. DebtRatio                               150000 non-null float64
  9. MonthlyIncome                           120269 non-null float64
  10. NumberOfOpenCreditLinesAndLoans         150000 non-null int64
  11. NumberOfTimes90DaysLate                 150000 non-null int64
  12. NumberRealEstateLoansOrLines            150000 non-null int64
  13. NumberOfTime60-89DaysPastDueNotWorse    150000 non-null int64
  14. NumberOfDependents                      146076 non-null float64
  15. dtypes: float64(4), int64(7)
  16. memory usage: 13.7 MB

MonthlyIncome 有缺失值
NumberOfDependents 有缺失值

name 含义
SeriousDlqin2yrs 出现90天或更长时间逾期行为
RevolvingUtilizationOfUnsecuredLines 贷款以及信用卡可用额度与总额度的比例
age 借款人借款年龄
NumberOfTime30-59DaysPastDueNotWorse 过去两年内出现35-59天逾期但是没有发展得更坏的次数
DebtRatio 每月偿还债务、赡养费和生活费用占月收入的比例
MonthlyIncome 月收入
NumberOfOpenCreditLinesAndLoans 开放式贷款和信贷数量
NumberOfTimes90DaysLate 过去两年内出现90天逾期或更坏的次数
NumberRealEstateLoansOrLines 抵押贷款和房地产贷款数量，包括房屋净值信贷额度
NumberOfTime60-89DaysPastDueNotWorse 过去两年内出现60-89天逾期但是没有发展得更坏的次数
NumberOfDependents 家庭中不包括自身的家属人数（配偶，子女等）

1. 去除重复值

  1. data.drop_duplicates(inplace = True)
  2. data.info()
  1. <class 'pandas.core.frame.DataFrame'>
  2. Int64Index: 149391 entries, 1 to 150000
  3. Data columns (total 11 columns):
  4. SeriousDlqin2yrs                        149391 non-null int64
  5. RevolvingUtilizationOfUnsecuredLines    149391 non-null float64
  6. age                                     149391 non-null int64
  7. NumberOfTime30-59DaysPastDueNotWorse    149391 non-null int64
  8. DebtRatio                               149391 non-null float64
  9. MonthlyIncome                           120170 non-null float64
  10. NumberOfOpenCreditLinesAndLoans         149391 non-null int64
  11. NumberOfTimes90DaysLate                 149391 non-null int64
  12. NumberRealEstateLoansOrLines            149391 non-null int64
  13. NumberOfTime60-89DaysPastDueNotWorse    149391 non-null int64
  14. NumberOfDependents                      145563 non-null float64
  15. dtypes: float64(4), int64(7)
  16. memory usage: 13.7 MB

删除行之后，最好恢复索引

  1. data.index = range(data.shape[0])
  1. data.info()
  1. <class 'pandas.core.frame.DataFrame'>
  2. RangeIndex: 149391 entries, 0 to 149390
  3. Data columns (total 11 columns):
  4. SeriousDlqin2yrs                        149391 non-null int64
  5. RevolvingUtilizationOfUnsecuredLines    149391 non-null float64
  6. age                                     149391 non-null int64
  7. NumberOfTime30-59DaysPastDueNotWorse    149391 non-null int64
  8. DebtRatio                               149391 non-null float64
  9. MonthlyIncome                           120170 non-null float64
  10. NumberOfOpenCreditLinesAndLoans         149391 non-null int64
  11. NumberOfTimes90DaysLate                 149391 non-null int64
  12. NumberRealEstateLoansOrLines            149391 non-null int64
  13. NumberOfTime60-89DaysPastDueNotWorse    149391 non-null int64
  14. NumberOfDependents                      145563 non-null float64
  15. dtypes: float64(4), int64(7)
  16. memory usage: 12.5 MB

2. 填补缺失值

  1. data.isnull().sum()
  1. SeriousDlqin2yrs                            0
  2. RevolvingUtilizationOfUnsecuredLines        0
  3. age                                         0
  4. NumberOfTime30-59DaysPastDueNotWorse        0
  5. DebtRatio                                   0
  6. MonthlyIncome                           29221
  7. NumberOfOpenCreditLinesAndLoans             0
  8. NumberOfTimes90DaysLate                     0
  9. NumberRealEstateLoansOrLines                0
  10. NumberOfTime60-89DaysPastDueNotWorse        0
  11. NumberOfDependents                       3828
  12. dtype: int64
  1. data.isnull().sum()/len(data)
  1. SeriousDlqin2yrs                        0.000000
  2. RevolvingUtilizationOfUnsecuredLines    0.000000
  3. age                                     0.000000
  4. NumberOfTime30-59DaysPastDueNotWorse    0.000000
  5. DebtRatio                               0.000000
  6. MonthlyIncome                           0.195601
  7. NumberOfOpenCreditLinesAndLoans         0.000000
  8. NumberOfTimes90DaysLate                 0.000000
  9. NumberRealEstateLoansOrLines            0.000000
  10. NumberOfTime60-89DaysPastDueNotWorse    0.000000
  11. NumberOfDependents                      0.025624
  12. dtype: float64
  1. 月收入的数据有将近20%是空值，根据业务判断，月收入是最重要的特征，必须填补这些缺失值，不能删除
  2. 家属人数的数据只有2%缺失，可以直接删掉，也可以填补
  1. data.isnull().mean() #这种写法求均值，等同于上一句的总和除以总数
  1. SeriousDlqin2yrs                        0.000000
  2. RevolvingUtilizationOfUnsecuredLines    0.000000
  3. age                                     0.000000
  4. NumberOfTime30-59DaysPastDueNotWorse    0.000000
  5. DebtRatio                               0.000000
  6. MonthlyIncome                           0.195601
  7. NumberOfOpenCreditLinesAndLoans         0.000000
  8. NumberOfTimes90DaysLate                 0.000000
  9. NumberRealEstateLoansOrLines            0.000000
  10. NumberOfTime60-89DaysPastDueNotWorse    0.000000
  11. NumberOfDependents                      0.025624
  12. dtype: float64

用均值填补家属人数

  1. data.NumberOfDependents.fillna(value = data.NumberOfDependents.mean(), inplace = True)
  1. data.info()
  1. <class 'pandas.core.frame.DataFrame'>
  2. RangeIndex: 149391 entries, 0 to 149390
  3. Data columns (total 11 columns):
  4. SeriousDlqin2yrs                        149391 non-null int64
  5. RevolvingUtilizationOfUnsecuredLines    149391 non-null float64
  6. age                                     149391 non-null int64
  7. NumberOfTime30-59DaysPastDueNotWorse    149391 non-null int64
  8. DebtRatio                               149391 non-null float64
  9. MonthlyIncome                           120170 non-null float64
  10. NumberOfOpenCreditLinesAndLoans         149391 non-null int64
  11. NumberOfTimes90DaysLate                 149391 non-null int64
  12. NumberRealEstateLoansOrLines            149391 non-null int64
  13. NumberOfTime60-89DaysPastDueNotWorse    149391 non-null int64
  14. NumberOfDependents                      149391 non-null float64
  15. dtypes: float64(4), int64(7)
  16. memory usage: 12.5 MB

填补收入字段的缺失值

结合业务推断原因：

  1. 高收入的客户来借款，更有意愿填写收入情况
  2. 低收入的客户来借款，填写收入情况的意愿更弱，避免收入情况影响银行借款的通过率
  3. 银行信息录入不完全

方案：

  1. 不可以用0值填补，否则低收入群体的收入特征与标签的相关性会很低
  2. 从业务人员处了解缺失值的产生原因
  3. 单个特征大量缺失，其他特征却是完整的，适合使用随机森林算法填补
  1. def fill_missing_rf(x, y, to_fill):
  2.     df = x.copy()
  3.     fill = df.loc[:, to_fill]
  4.     df = pd.concat([df.loc[:, df.columns != to_fill], pd.DataFrame(y)], axis = 1)
  6.     Ytrain = fill[fill.notnull()] 
  7.     Ytest = fill[fill.isnull()]
  8.     Xtrain = df.iloc[Ytrain.index, :]
  9.     Xtest = df.iloc[Ytest.index, :]
  11.     from sklearn.ensemble import RandomForestRegressor as RFR
  13.     rfr = RFR(n_estimators = 100).fit(Xtrain, Ytrain)
  14.     Ypredict = rfr.predict(Xtest)
  16.     return Ypredict
  1. x = data.iloc[:, 1:]
  2. y = data.SeriousDlqin2yrs
  1. x.shape
  1. (149391, 10)
  1. y.shape
  1. (149391,)
  1. data.loc[data.loc[:, 'MonthlyIncome'].isnull(), 'MonthlyIncome'] = fill_missing_rf(x, y, 'MonthlyIncome')
  1. data.info()
  1. <class 'pandas.core.frame.DataFrame'>
  2. RangeIndex: 149391 entries, 0 to 149390
  3. Data columns (total 11 columns):
  4. SeriousDlqin2yrs                        149391 non-null int64
  5. RevolvingUtilizationOfUnsecuredLines    149391 non-null float64
  6. age                                     149391 non-null int64
  7. NumberOfTime30-59DaysPastDueNotWorse    149391 non-null int64
  8. DebtRatio                               149391 non-null float64
  9. MonthlyIncome                           149391 non-null float64
  10. NumberOfOpenCreditLinesAndLoans         149391 non-null int64
  11. NumberOfTimes90DaysLate                 149391 non-null int64
  12. NumberRealEstateLoansOrLines            149391 non-null int64
  13. NumberOfTime60-89DaysPastDueNotWorse    149391 non-null int64
  14. NumberOfDependents                      149391 non-null float64
  15. dtypes: float64(4), int64(7)
  16. memory usage: 12.5 MB
  1. data.loc[:, 'MonthlyIncome'].shape[0] - 120170
  1. 29221

3. 处理异常值

“异常”是相对的，处理异常值要机器学习方法结合业务逻辑

  1. 异常值是错误的数据，如收入为负数，删除异常值
  2. 异常值是正确的数据，如极高收入或0收入，保留异常值，并重点研究

找异常值的方法：

  1. 逻辑回归和信用评分卡 - 图12
  2. 箱线图
  3. 描述性统计，观察数据的分布情况
  1. data.describe()
SeriousDlqin2yrs RevolvingUtilizationOfUnsecuredLines age NumberOfTime30-59DaysPastDueNotWorse DebtRatio MonthlyIncome NumberOfOpenCreditLinesAndLoans NumberOfTimes90DaysLate NumberRealEstateLoansOrLines NumberOfTime60-89DaysPastDueNotWorse NumberOfDependents
count 149391.000000 149391.000000 149391.000000 149391.000000 149391.000000 1.493910e+05 149391.000000 149391.000000 149391.000000 149391.000000 149391.000000
mean 0.066999 6.071087 52.306237 0.393886 354.436740 5.429083e+03 8.480892 0.238120 1.022391 0.212503 0.759863
std 0.250021 250.263672 14.725962 3.852953 2041.843455 1.324520e+04 5.136515 3.826165 1.130196 3.810523 1.101749
min 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000e+00 0.000000 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.030132 41.000000 0.000000 0.177441 1.800000e+03 5.000000 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.154235 52.000000 0.000000 0.368234 4.429000e+03 8.000000 0.000000 1.000000 0.000000 0.000000
75% 0.000000 0.556494 63.000000 0.000000 0.875279 7.416000e+03 11.000000 0.000000 2.000000 0.000000 1.000000
max 1.000000 50708.000000 109.000000 98.000000 329664.000000 3.008750e+06 58.000000 98.000000 54.000000 98.000000 20.000000 
  1. data.describe().T
count mean std min 25% 50% 75% max
SeriousDlqin2yrs 149391.0 0.066999 0.250021 0.0 0.000000 0.000000 0.000000 1.0
RevolvingUtilizationOfUnsecuredLines 149391.0 6.071087 250.263672 0.0 0.030132 0.154235 0.556494 50708.0
age 149391.0 52.306237 14.725962 0.0 41.000000 52.000000 63.000000 109.0
NumberOfTime30-59DaysPastDueNotWorse 149391.0 0.393886 3.852953 0.0 0.000000 0.000000 0.000000 98.0
DebtRatio 149391.0 354.436740 2041.843455 0.0 0.177441 0.368234 0.875279 329664.0
MonthlyIncome 149391.0 5429.082606 13245.195298 0.0 1800.000000 4429.000000 7416.000000 3008750.0
NumberOfOpenCreditLinesAndLoans 149391.0 8.480892 5.136515 0.0 5.000000 8.000000 11.000000 58.0
NumberOfTimes90DaysLate 149391.0 0.238120 3.826165 0.0 0.000000 0.000000 0.000000 98.0
NumberRealEstateLoansOrLines 149391.0 1.022391 1.130196 0.0 0.000000 1.000000 2.000000 54.0
NumberOfTime60-89DaysPastDueNotWorse 149391.0 0.212503 3.810523 0.0 0.000000 0.000000 0.000000 98.0
NumberOfDependents 149391.0 0.759863 1.101749 0.0 0.000000 0.000000 1.000000 20.0 
  1. data.describe([0.01, 0.1, 0.25, .5, .75, .9, .99]).T
count mean std min 1% 10% 25% 50% 75% 90% 99% max
SeriousDlqin2yrs 149391.0 0.066999 0.250021 0.0 0.0 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 1.0
RevolvingUtilizationOfUnsecuredLines 149391.0 6.071087 250.263672 0.0 0.0 0.003199 0.030132 0.154235 0.556494 0.978007 1.093922 50708.0
age 149391.0 52.306237 14.725962 0.0 24.0 33.000000 41.000000 52.000000 63.000000 72.000000 87.000000 109.0
NumberOfTime30-59DaysPastDueNotWorse 149391.0 0.393886 3.852953 0.0 0.0 0.000000 0.000000 0.000000 0.000000 1.000000 4.000000 98.0
DebtRatio 149391.0 354.436740 2041.843455 0.0 0.0 0.034991 0.177441 0.368234 0.875279 1275.000000 4985.100000 329664.0
MonthlyIncome 149391.0 5429.082606 13245.195298 0.0 0.0 0.190000 1800.000000 4429.000000 7416.000000 10800.000000 23256.100000 3008750.0
NumberOfOpenCreditLinesAndLoans 149391.0 8.480892 5.136515 0.0 0.0 3.000000 5.000000 8.000000 11.000000 15.000000 24.000000 58.0
NumberOfTimes90DaysLate 149391.0 0.238120 3.826165 0.0 0.0 0.000000 0.000000 0.000000 0.000000 0.000000 3.000000 98.0
NumberRealEstateLoansOrLines 149391.0 1.022391 1.130196 0.0 0.0 0.000000 0.000000 1.000000 2.000000 2.000000 4.000000 54.0
NumberOfTime60-89DaysPastDueNotWorse 149391.0 0.212503 3.810523 0.0 0.0 0.000000 0.000000 0.000000 0.000000 0.000000 2.000000 98.0
NumberOfDependents 149391.0 0.759863 1.101749 0.0 0.0 0.000000 0.000000 0.000000 1.000000 2.000000 4.000000 20.0

四个指标有异常值：

  1. age年龄 最小值为0，不符合银行业务规定
  2. NumberOfTime30-59DaysPastDueNotWorse 最大值为98，两年内98次逾期30天以上，这是不可能的
  3. NumberOfTime60-89DaysPastDueNotWorse 同上
  4. NumberOfTimes90DaysLate 同上
    需要咨询业务人员逾期次数的计算方法，如果98是正常值，那么这些客户对应的标签应该都是“坏”标签。
  1. data[data['age'] == 0]
SeriousDlqin2yrs RevolvingUtilizationOfUnsecuredLines age NumberOfTime30-59DaysPastDueNotWorse DebtRatio MonthlyIncome NumberOfOpenCreditLinesAndLoans NumberOfTimes90DaysLate NumberRealEstateLoansOrLines NumberOfTime60-89DaysPastDueNotWorse NumberOfDependents
65553 0 1.0 0 1 0.436927 6000.0 6 0 2 0 2.0 
  1. (data['age'] == 0).sum()
  1. 1
  1. data = data[data['age'] != 0]
  2. (data['age'] == 0).sum()
  1. 0
  1. data.shape
  1. (149390, 11)
  1. data.describe().T
count mean std min 25% 50% 75% max
SeriousDlqin2yrs 149390.0 0.066999 0.250021 0.0 0.000000 0.000000 0.000000 1.0
RevolvingUtilizationOfUnsecuredLines 149390.0 6.071121 250.264509 0.0 0.030132 0.154234 0.556491 50708.0
age 149390.0 52.306587 14.725390 21.0 41.000000 52.000000 63.000000 109.0
NumberOfTime30-59DaysPastDueNotWorse 149390.0 0.393882 3.852966 0.0 0.000000 0.000000 0.000000 98.0
DebtRatio 149390.0 354.439110 2041.850084 0.0 0.177441 0.368233 0.875294 329664.0
MonthlyIncome 149390.0 5429.078785 13245.239547 0.0 1800.000000 4429.000000 7416.000000 3008750.0
NumberOfOpenCreditLinesAndLoans 149390.0 8.480909 5.136528 0.0 5.000000 8.000000 11.000000 58.0
NumberOfTimes90DaysLate 149390.0 0.238122 3.826177 0.0 0.000000 0.000000 0.000000 98.0
NumberRealEstateLoansOrLines 149390.0 1.022384 1.130196 0.0 0.000000 1.000000 2.000000 54.0
NumberOfTime60-89DaysPastDueNotWorse 149390.0 0.212504 3.810536 0.0 0.000000 0.000000 0.000000 98.0
NumberOfDependents 149390.0 0.759855 1.101748 0.0 0.000000 0.000000 1.000000 20.0 
  1. data[data['NumberOfTime30-59DaysPastDueNotWorse'] > 90].head()
SeriousDlqin2yrs RevolvingUtilizationOfUnsecuredLines age NumberOfTime30-59DaysPastDueNotWorse DebtRatio MonthlyIncome NumberOfOpenCreditLinesAndLoans NumberOfTimes90DaysLate NumberRealEstateLoansOrLines NumberOfTime60-89DaysPastDueNotWorse NumberOfDependents
1732 1 1.0 27 98 0.0 2700.000000 0 98 0 98 0.0
2285 0 1.0 22 98 0.0 1340.388908 0 98 0 98 0.0
3883 0 1.0 38 98 12.0 2281.400000 0 98 0 98 0.0
4416 0 1.0 21 98 0.0 0.000000 0 98 0 98 0.0
4704 0 1.0 21 98 0.0 2000.000000 0 98 0 98 0.0 
  1. data[data['NumberOfTime30-59DaysPastDueNotWorse'] > 90].count()
  1. SeriousDlqin2yrs                        225
  2. RevolvingUtilizationOfUnsecuredLines    225
  3. age                                     225
  4. NumberOfTime30-59DaysPastDueNotWorse    225
  5. DebtRatio                               225
  6. MonthlyIncome                           225
  7. NumberOfOpenCreditLinesAndLoans         225
  8. NumberOfTimes90DaysLate                 225
  9. NumberRealEstateLoansOrLines            225
  10. NumberOfTime60-89DaysPastDueNotWorse    225
  11. NumberOfDependents                      225
  12. dtype: int64
  1. data['NumberOfTimes90DaysLate'].value_counts()
  1. 0     141107
  2. 1       5232
  3. 2       1555
  4. 3        667
  5. 4        291
  6. 98       220
  7. 5        131
  8. 6         80
  9. 7         38
  10. 8         21
  11. 9         19
  12. 10         8
  13. 11         5
  14. 96         5
  15. 13         4
  16. 12         2
  17. 14         2
  18. 15         2
  19. 17         1
  20. Name: NumberOfTimes90DaysLate, dtype: int64
  1. data = data[data['NumberOfTimes90DaysLate'] < 90]
  2. data.describe().T
count mean std min 25% 50% 75% max
SeriousDlqin2yrs 149165.0 0.066188 0.248612 0.0 0.000000 0.000000 0.000000 1.0
RevolvingUtilizationOfUnsecuredLines 149165.0 6.078770 250.453111 0.0 0.030033 0.153615 0.553698 50708.0
age 149165.0 52.331076 14.714114 21.0 41.000000 52.000000 63.000000 109.0
NumberOfTime30-59DaysPastDueNotWorse 149165.0 0.246720 0.698935 0.0 0.000000 0.000000 0.000000 13.0
DebtRatio 149165.0 354.963542 2043.344496 0.0 0.178211 0.368619 0.876994 329664.0
MonthlyIncome 149165.0 5433.077995 13254.287999 0.0 1800.000000 4440.000000 7422.000000 3008750.0
NumberOfOpenCreditLinesAndLoans 149165.0 8.493688 5.129841 0.0 5.000000 8.000000 11.000000 58.0
NumberOfTimes90DaysLate 149165.0 0.090725 0.486354 0.0 0.000000 0.000000 0.000000 17.0
NumberRealEstateLoansOrLines 149165.0 1.023927 1.130350 0.0 0.000000 1.000000 2.000000 54.0
NumberOfTime60-89DaysPastDueNotWorse 149165.0 0.065069 0.330675 0.0 0.000000 0.000000 0.000000 11.0
NumberOfDependents 149165.0 0.760325 1.102024 0.0 0.000000 0.000000 1.000000 20.0

4. 恢复索引

  1. data.info()
  1. <class 'pandas.core.frame.DataFrame'>
  2. Int64Index: 149165 entries, 0 to 149390
  3. Data columns (total 11 columns):
  4. SeriousDlqin2yrs                        149165 non-null int64
  5. RevolvingUtilizationOfUnsecuredLines    149165 non-null float64
  6. age                                     149165 non-null int64
  7. NumberOfTime30-59DaysPastDueNotWorse    149165 non-null int64
  8. DebtRatio                               149165 non-null float64
  9. MonthlyIncome                           149165 non-null float64
  10. NumberOfOpenCreditLinesAndLoans         149165 non-null int64
  11. NumberOfTimes90DaysLate                 149165 non-null int64
  12. NumberRealEstateLoansOrLines            149165 non-null int64
  13. NumberOfTime60-89DaysPastDueNotWorse    149165 non-null int64
  14. NumberOfDependents                      149165 non-null float64
  15. dtypes: float64(4), int64(7)
  16. memory usage: 13.7 MB
  1. data.index = range(len(data))
  1. data.info()
  1. <class 'pandas.core.frame.DataFrame'>
  2. RangeIndex: 149165 entries, 0 to 149164
  3. Data columns (total 11 columns):
  4. SeriousDlqin2yrs                        149165 non-null int64
  5. RevolvingUtilizationOfUnsecuredLines    149165 non-null float64
  6. age                                     149165 non-null int64
  7. NumberOfTime30-59DaysPastDueNotWorse    149165 non-null int64
  8. DebtRatio                               149165 non-null float64
  9. MonthlyIncome                           149165 non-null float64
  10. NumberOfOpenCreditLinesAndLoans         149165 non-null int64
  11. NumberOfTimes90DaysLate                 149165 non-null int64
  12. NumberRealEstateLoansOrLines            149165 non-null int64
  13. NumberOfTime60-89DaysPastDueNotWorse    149165 non-null int64
  14. NumberOfDependents                      149165 non-null float64
  15. dtypes: float64(4), int64(7)
  16. memory usage: 12.5 MB

5. 标准化消除偏态，同一量纲

数据偏态严重，量纲不统一，需要标准化，但是标准化后的数据大小和范围变化，无法指导业务人员操作。
这也能看出，业务人员直接根据实际数值的大小判断是不科学的。但为了便于业务操作，所以不进行标准化处理。

6. 上采样平衡样本，解决样本不均衡问题

虽然我们致力于防范信用风险，但实际上违约的人相对于总数来说并不多，并且，不是所有违约的人都是有意不还钱，可能是忘了还款日，也可能是遇到了困难，这两种人以后是会还钱的。
而银行想要识别的，只是那些“恶意违约”的人。而这部分人造成的损失极大，人数却极少，样本就不会均衡。

  1. y.value_counts()
  1. 0    139382
  2. 1     10009
  3. Name: SeriousDlqin2yrs, dtype: int64
  1. n_sample = x.shape[0]
  3. n_0_sample = y.value_counts()[0]
  4. n_1_sample = y.value_counts()[1]
  6. print('样本个数：{}；0占{:.2%}；1占{:.2%}'.format(n_sample, n_0_sample/n_sample, n_1_sample/n_sample))
  1. 样本个数：149391；0占93.30%；1占6.70%

imbalance learn

  1. import imblearn
  2. from imblearn.over_sampling import SMOTE
  1. x = data.iloc[:, 1:]
  2. y = data.SeriousDlqin2yrs 
  4. sm = SMOTE(random_state = 42) # 实例化
  5. x, y = sm.fit_sample(x, y) # 返回上采样后的特征矩阵和标签
  6. y = pd.Series(y)
  7. # 采样后的y是数组，需要转换成Series后才可以使用value_counts()方法
  9. n_sample = x.shape[0]
  11. n_0_sample = y.value_counts()[0]
  12. n_1_sample = y.value_counts()[1]
  14. print('样本个数：{}；0占{:.2%}；1占{:.2%}'.format(n_sample, n_0_sample/n_sample, n_1_sample/n_sample))
  1. 样本个数：278584；0占50.00%；1占50.00%

7. 分训练集和测试集

  1. Xtrain, Xvali, Ytrain, Yvali = train_test_split(x, y, test_size = 0.3, random_state = 420)
  1. model_data = pd.concat([Ytrain, Xtrain], axis = 1)
  2. model_data.head()
SeriousDlqin2yrs RevolvingUtilizationOfUnsecuredLines age NumberOfTime30-59DaysPastDueNotWorse DebtRatio MonthlyIncome NumberOfOpenCreditLinesAndLoans NumberOfTimes90DaysLate NumberRealEstateLoansOrLines NumberOfTime60-89DaysPastDueNotWorse NumberOfDependents
81602 0 0.015404 53 0 0.121802 4728.0 5 0 0 0 0.000000
149043 0 0.168311 63 0 0.141964 1119.0 5 0 0 0 0.000000
215073 1 1.063570 39 1 0.417663 3500.0 5 1 0 2 3.716057
66278 0 0.088684 73 0 0.522822 5301.0 11 0 2 0 0.000000
157084 1 0.622999 53 0 0.423650 13000.0 9 0 2 0 0.181999 
  1. model_data.index = range(model_data.shape[0])
  2. model_data.head()
SeriousDlqin2yrs RevolvingUtilizationOfUnsecuredLines age NumberOfTime30-59DaysPastDueNotWorse DebtRatio MonthlyIncome NumberOfOpenCreditLinesAndLoans NumberOfTimes90DaysLate NumberRealEstateLoansOrLines NumberOfTime60-89DaysPastDueNotWorse NumberOfDependents
0 0 0.015404 53 0 0.121802 4728.0 5 0 0 0 0.000000
1 0 0.168311 63 0 0.141964 1119.0 5 0 0 0 0.000000
2 1 1.063570 39 1 0.417663 3500.0 5 1 0 2 3.716057
3 0 0.088684 73 0 0.522822 5301.0 11 0 2 0 0.000000
4 1 0.622999 53 0 0.423650 13000.0 9 0 2 0 0.181999 
  1. vali_data = pd.concat([Yvali, Xvali], axis = 1)
  2. vali_data.index = range(vali_data.shape[0])
  3. vali_data.head()
SeriousDlqin2yrs RevolvingUtilizationOfUnsecuredLines age NumberOfTime30-59DaysPastDueNotWorse DebtRatio MonthlyIncome NumberOfOpenCreditLinesAndLoans NumberOfTimes90DaysLate NumberRealEstateLoansOrLines NumberOfTime60-89DaysPastDueNotWorse NumberOfDependents
0 0 0.000000 58 0 0.000481 2080.000000 4 0 0 0 0.000000
1 1 0.588870 44 0 0.198193 29373.217358 13 0 2 0 2.504880
2 0 0.057460 64 0 0.021830 6000.000000 4 0 0 0 0.000000
3 0 0.011585 52 0 0.139685 5583.000000 8 0 1 0 0.000000
4 1 0.663034 53 0 0.399663 4800.000000 12 0 0 0 0.201706

将数据保存成csv格式文件，便于复用

  1. model_data.to_csv(r'C:\Users\chenh\机器学习Sklearn\model_data.csv')
  2. vali_data.to_csv(r'C:\Users\chenh\机器学习Sklearn\vali_data.csv')

分箱

分箱的本质就是离散化连续变量，类似聚类。

  1. 分多少个箱子才合适？

初始判断：既然是将连续型变量离散化，箱子个数就不能太多，最多不能超过十个 进一步判断：分箱会损失信息，箱子越少，信息损失越多。因此需要一个指标，衡量特征上的信息量以及特征对预测函数的贡献：

逻辑回归和信用评分卡 - 图13> 其中，逻辑回归和信用评分卡 - 图14

  1. N是特征上箱子的数量
  2. good表示这个箱内的优质客户数量，bad表示这个箱内的违约可能性高的客户数量
  3. WOE即证据权重，衡量违约概率，是优质客户数量比上“坏”客户数量的比例的对数，形似对数几率
  4. IV并非越大越好。分箱越多，IV必然越小，因为信息损失会非常多；分箱越少，IV必然越大
IV值 特征对预测函数的贡献
<0.03 特征几乎不带有效信息，对模型没有贡献，这种特征可以删除
0.03-0.09 有效信息很少，贡献低
0.1-0.29 有效信息一般，贡献中
0.3~0.49 有效信息较多，贡献较高
>=.5 有效信息非常多，贡献非常高，但是可疑：可能是特征与标签间具有线性关系，但没有预测性
  1. 分箱要达成什么效果？

组间差异大，组内差异小：

不同属性的人有不同的分数，在同一个箱子内的人的属性尽量相似，不同箱子的人的属性尽量不同

对于评分卡来说：

在同一个箱子内的人的违约概率相似；不同箱子的人的违约概率差距很大，即WOE差距要大

可以使用卡方检验来对比两个箱子之间的相似性：

如果两个箱子之间卡方检验的P值很大，说明他们非常相似，加可以把他们合为一个箱子

  1. 分箱步骤

1）把连续型变量分成一组数量较多的分类型变量，比如，将几万个样本分成100组，或50组 2）确保每一组中都要包含两种类别的样本，否则IV值会无法计算 3）对相邻的组进行卡方检验，卡方检验的P值很大的组进行合并，直到数据中的组数小于设定的N箱为止 4）我们让一个特征分别分成逻辑回归和信用评分卡 - 图15箱，观察每个分箱个数下的IV值如何变化，找出最适合的分箱个数 5）分箱完毕后，我们计算每箱的WOE值，观察分箱效果 这些步骤都完成后，可以对各个特征都进行分箱，然后观察每个特征的IV值，以此来挑选用来分箱的特征

1. 等频分箱

以’age’为例，把连续型变量分成一组数量较多的分类型变量

  1. model_data.age.head()
  1. 0    53
  2. 1    63
  3. 2    39
  4. 3    73
  5. 4    53
  6. Name: age, dtype: int64
  1. # pd.qcut()基于分位数分箱，只能处一维数据
  2. model_data['qcut'], updown = pd.qcut(model_data['age']
  3.                                    , retbins = True # 要求返回结构为索引的样本索引，元素为分到的箱子的Series
  4.                                    , q = 20 # 要分箱的数量
  5.                                     )
  6. '''
  7. 现在返回两个值：
  8. 1. 每个样本所属的箱子
  9. 2. 由所有箱子的上界和下界构成的数组  
  10. '''
  1. '\n现在返回两个值：\n1. 每个样本所属的箱子\n2. 由所有箱子的上界和下界构成的数组  \n'
  1. model_data.qcut.head()
  1. 0    (52.0, 54.0]
  2. 1    (61.0, 64.0]
  3. 2    (36.0, 39.0]
  4. 3    (68.0, 74.0]
  5. 4    (52.0, 54.0]
  6. Name: qcut, dtype: category
  7. Categories (20, interval[float64]): [(20.999, 28.0] < (28.0, 31.0] < (31.0, 34.0] < (34.0, 36.0] ... (61.0, 64.0] < (64.0, 68.0] < (68.0, 74.0] < (74.0, 107.0]]
  1. updown
  1. array([ 21.,  28.,  31.,  34.,  36.,  39.,  41.,  43.,  45.,  46.,  48.,
  2.         50.,  52.,  54.,  56.,  58.,  61.,  64.,  68.,  74., 107.])

2. 确保每一组中都包含两种类别的样本

  1. model_data.qcut.value_counts()
  1. (36.0, 39.0]      12613
  2. (20.999, 28.0]    11831
  3. (58.0, 61.0]      11361
  4. (48.0, 50.0]      11138
  5. (46.0, 48.0]      10980
  6. (31.0, 34.0]      10810
  7. (50.0, 52.0]      10544
  8. (43.0, 45.0]      10364
  9. (61.0, 64.0]      10197
  10. (39.0, 41.0]       9806
  11. (41.0, 43.0]       9690
  12. (52.0, 54.0]       9678
  13. (28.0, 31.0]       9475
  14. (74.0, 107.0]      9122
  15. (64.0, 68.0]       8933
  16. (54.0, 56.0]       8723
  17. (68.0, 74.0]       8649
  18. (56.0, 58.0]       7886
  19. (34.0, 36.0]       7490
  20. (45.0, 46.0]       5718
  21. Name: qcut, dtype: int64
  1. model_data[model_data.SeriousDlqin2yrs == 0].groupby(by = 'qcut').count()['SeriousDlqin2yrs']
  1. qcut
  2. (20.999, 28.0]    4243
  3. (28.0, 31.0]      3571
  4. (31.0, 34.0]      4075
  5. (34.0, 36.0]      2908
  6. (36.0, 39.0]      5182
  7. (39.0, 41.0]      3956
  8. (41.0, 43.0]      4002
  9. (43.0, 45.0]      4389
  10. (45.0, 46.0]      2419
  11. (46.0, 48.0]      4813
  12. (48.0, 50.0]      4900
  13. (50.0, 52.0]      4728
  14. (52.0, 54.0]      4681
  15. (54.0, 56.0]      4677
  16. (56.0, 58.0]      4483
  17. (58.0, 61.0]      6583
  18. (61.0, 64.0]      6968
  19. (64.0, 68.0]      6623
  20. (68.0, 74.0]      6753
  21. (74.0, 107.0]     7737
  22. Name: SeriousDlqin2yrs, dtype: int64
  1. model_data[model_data.SeriousDlqin2yrs == 1].groupby(by = 'qcut').count()['SeriousDlqin2yrs']
  1. qcut
  2. (20.999, 28.0]    7588
  3. (28.0, 31.0]      5904
  4. (31.0, 34.0]      6735
  5. (34.0, 36.0]      4582
  6. (36.0, 39.0]      7431
  7. (39.0, 41.0]      5850
  8. (41.0, 43.0]      5688
  9. (43.0, 45.0]      5975
  10. (45.0, 46.0]      3299
  11. (46.0, 48.0]      6167
  12. (48.0, 50.0]      6238
  13. (50.0, 52.0]      5816
  14. (52.0, 54.0]      4997
  15. (54.0, 56.0]      4046
  16. (56.0, 58.0]      3403
  17. (58.0, 61.0]      4778
  18. (61.0, 64.0]      3229
  19. (64.0, 68.0]      2310
  20. (68.0, 74.0]      1896
  21. (74.0, 107.0]     1385
  22. Name: SeriousDlqin2yrs, dtype: int64
  1. # 统计各分箱中，0和1的数量
  2. count_y0 = model_data[model_data.SeriousDlqin2yrs == 0].groupby(by = 'qcut').count()['SeriousDlqin2yrs']
  3. count_y1 = model_data[model_data.SeriousDlqin2yrs == 1].groupby(by = 'qcut').count()['SeriousDlqin2yrs']
  5. # num_bins值分别各个区间的上界，下界，0出现的次数，1出现的次数
  6. num_bins = [*zip(updown, updown[1:], count_y0, count_y1)] # 【注意】 zip会按照最短的哪一个列表来结合
  8. num_bins
  1. [(21.0, 28.0, 4243, 7588),
  2.  (28.0, 31.0, 3571, 5904),
  3.  (31.0, 34.0, 4075, 6735),
  4.  (34.0, 36.0, 2908, 4582),
  5.  (36.0, 39.0, 5182, 7431),
  6.  (39.0, 41.0, 3956, 5850),
  7.  (41.0, 43.0, 4002, 5688),
  8.  (43.0, 45.0, 4389, 5975),
  9.  (45.0, 46.0, 2419, 3299),
  10.  (46.0, 48.0, 4813, 6167),
  11.  (48.0, 50.0, 4900, 6238),
  12.  (50.0, 52.0, 4728, 5816),
  13.  (52.0, 54.0, 4681, 4997),
  14.  (54.0, 56.0, 4677, 4046),
  15.  (56.0, 58.0, 4483, 3403),
  16.  (58.0, 61.0, 6583, 4778),
  17.  (61.0, 64.0, 6968, 3229),
  18.  (64.0, 68.0, 6623, 2310),
  19.  (68.0, 74.0, 6753, 1896),
  20.  (74.0, 107.0, 7737, 1385)]
  1. for i in range(20):
  2.     # 如果第一个组没有包含正样本或负样本，向后合并
  3.     if 0 in num_bins[0][2:]:
  4.         num_bins[0:2] = [(num_bins[0][0] # 取第1组中第1个元素，作为新组的上限
  5.                         , num_bins[1][1] # 取第2组中第2个元素，作为新组的下限
  6.                         , num_bins[0][2] + num_bins[1][2] # 第1组和第2组的0出现的次数相加
  7.                         , num_bins[0][3] + num_bins[1][3] # 第1组和第2组的1出现的次数相加
  8.                          )]
  9.         continue # 跳出本次循环，也跳过了下面的代码
  10.         '''
  11.         如果发现第一组没有包含正样本或负样本，在将其与第二组合并后，还要检查新生成的组是否包含正样本或负样本
  12.         如果第一组中有正样本或负样本，则直接进入下一段代码
  13.         '''
  14.     for i in range(len(num_bins)):
  15.         # 执行前一段代码后，确认第一个组中有正样本或负样本，如果其他组没有，向前合并
  16.         if 0 in num_bins[i][2:]:
  17.             '''
  18.             第一次循环(i=0)时，num_bins[0]已被处理过，不会执行if下面的代码
  19.             第二次循环(i=1)时，num_bins[1]可能包含正样本或负样本，也可能不包含
  20.             '''
  21.             num_bins[i-1:i+1] = [(num_bins[i-1][0]
  22.                                 , num_bins[i][1]
  23.                                 , num_bins[i-1][2] + num_bins[i][2]
  24.                                 , num_bins[i-1][3] + num_bins[i][3]
  25.                                  )]
  26.             break 
  27.     else:
  28.         break

3. 定义WOE和IV函数

  1. num_bins
  1. [(21.0, 28.0, 4243, 7588),
  2.  (28.0, 31.0, 3571, 5904),
  3.  (31.0, 34.0, 4075, 6735),
  4.  (34.0, 36.0, 2908, 4582),
  5.  (36.0, 39.0, 5182, 7431),
  6.  (39.0, 41.0, 3956, 5850),
  7.  (41.0, 43.0, 4002, 5688),
  8.  (43.0, 45.0, 4389, 5975),
  9.  (45.0, 46.0, 2419, 3299),
  10.  (46.0, 48.0, 4813, 6167),
  11.  (48.0, 50.0, 4900, 6238),
  12.  (50.0, 52.0, 4728, 5816),
  13.  (52.0, 54.0, 4681, 4997),
  14.  (54.0, 56.0, 4677, 4046),
  15.  (56.0, 58.0, 4483, 3403),
  16.  (58.0, 61.0, 6583, 4778),
  17.  (61.0, 64.0, 6968, 3229),
  18.  (64.0, 68.0, 6623, 2310),
  19.  (68.0, 74.0, 6753, 1896),
  20.  (74.0, 107.0, 7737, 1385)]
  1. columns = ['min', 'max', 'count_0', 'count_1']
  2. df = pd.DataFrame(num_bins, columns = columns)
  4. df['total'] = df['count_0'] + df['count_1']
  5. df['percentage'] = df['total']/df['total'].sum()
  7. df['bad_rate'] = df['count_1']/df['total']
  8. df['bad%'] = df['count_1']/df['count_1'].sum()
  9. df['good%'] = df['count_0']/df['count_0'].sum()
  11. df['woe'] = np.log(df['good%']/df['bad%'])
  13. df.head()
min max count_0 count_1 total percentage bad_rate bad% good% woe
0 21.0 28.0 4243 7588 11831 0.060669 0.641366 0.077972 0.043433 -0.585133
1 28.0 31.0 3571 5904 9475 0.048588 0.623113 0.060668 0.036554 -0.506620
2 31.0 34.0 4075 6735 10810 0.055434 0.623034 0.069207 0.041713 -0.506283
3 34.0 36.0 2908 4582 7490 0.038409 0.611749 0.047083 0.029767 -0.458506
4 36.0 39.0 5182 7431 12613 0.064679 0.589154 0.076359 0.053045 -0.364305 
  1. def get_woe(num_bins):
  2.     columns = ['min', 'max', 'count_0', 'count_1']
  3.     df = pd.DataFrame(num_bins, columns = columns)
  5.     df['total'] = df['count_0'] + df['count_1']
  6.     df['percentage'] = df['total']/df['total'].sum()
  8.     df['bad_rate'] = df['count_1']/df['total']
  9.     df['bad%'] = df['count_1']/df['count_1'].sum()
  10.     df['good%'] = df['count_0']/df['count_0'].sum()
  12.     df['woe'] = np.log(df['good%']/df['bad%'])
  14.     return df
  1. def get_iv(bins_df):
  2.     rate = bins_df['good%'] - bins_df['bad%']
  3.     iv = np.sum(rate * bins_df['woe'])
  4.     return iv
  6. iv_age = get_iv(df)
  7. iv_age
  1. 0.3538235234736649
IV值 特征对预测函数的贡献
<0.03 特征几乎不带有效信息，对模型没有贡献，这种特征可以删除
0.03-0.09 有效信息很少，贡献低
0.1-0.29 有效信息一般，贡献中
0.3~0.49 有效信息较多，贡献较高
>=.5 有效信息非常多，贡献非常高，但是可疑：可能是特征与标签间具有线性关系，但没有预测性

4. 卡方检验，合并箱体，画出IV曲线

  1. df.head()
min max count_0 count_1 total percentage bad_rate bad% good% woe
0 21.0 28.0 4243 7588 11831 0.060669 0.641366 0.077972 0.043433 -0.585133
1 28.0 31.0 3571 5904 9475 0.048588 0.623113 0.060668 0.036554 -0.506620
2 31.0 34.0 4075 6735 10810 0.055434 0.623034 0.069207 0.041713 -0.506283
3 34.0 36.0 2908 4582 7490 0.038409 0.611749 0.047083 0.029767 -0.458506
4 36.0 39.0 5182 7431 12613 0.064679 0.589154 0.076359 0.053045 -0.364305 
  1. pd.DataFrame(num_bins, columns = columns).head()
min max count_0 count_1
0 21.0 28.0 4243 7588
1 28.0 31.0 3571 5904
2 31.0 34.0 4075 6735
3 34.0 36.0 2908 4582
4 36.0 39.0 5182 7431

(total, percentage, bad_rate, bad%, good%, woe)和(count_0, count_1)线性相关
卡方检验只需要(count_0, count_1)

  1. import scipy
  3. num_bins_ = num_bins.copy()
  5. IV = []
  6. axisx = []
  8. while len(num_bins_) > 2:
  9.     pvs = []
  10.     for i in range(len(num_bins_) - 1):
  11.         x1 = num_bins_[i][2:]
  12.         x2 = num_bins_[i+1][2:]
  13.       # chi2v = scipy.stats.chi2_contingency([x1, x2])[0] 返回卡方值
  14.         pv = scipy.stats.chi2_contingency([x1, x2])[1] # 返回p值
  15.         pvs.append(pv) 
  17.     i = pvs.index(max(pvs))
  18.     num_bins_[i:i+2] = [(num_bins_[i][0], num_bins_[i+1][1],
  19.                          num_bins_[i][2] + num_bins_[i+1][2],
  20.                          num_bins_[i][3] + num_bins_[i+1][3])]
  22.     bins_df = get_woe(num_bins_)
  23.     axisx.append(len(num_bins_))
  24.     IV.append(get_iv(bins_df))
  26. plt.figure()
  27. plt.plot(axisx, IV)
  28. plt.xticks(axisx)
  29. plt.xlabel('number of box')
  30. plt.ylabel('IV')
  1. Text(0, 0.5, 'IV')

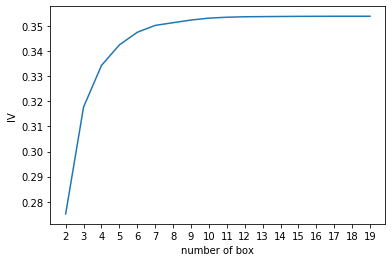
output_130_1.png

对于特征’age’来说，最佳箱数为6

5. 用最佳分箱数分箱，并验证分箱结果

  1. def get_bin(num_bins_, n):
  2.     while len(num_bins_) > n:
  3.         pvs = []
  4.         for i in range(len(num_bins_) - 1):
  5.             x1 = num_bins_[i][2:]
  6.             x2 = num_bins_[i+1][2:]
  7.           # chi2v = scipy.stats.chi2_contingency([x1, x2])[0] 返回卡方值
  8.             pv = scipy.stats.chi2_contingency([x1, x2])[1] # 返回p值
  9.             pvs.append(pv) 
  11.         i = pvs.index(max(pvs))
  12.         num_bins_[i:i+2] = [(num_bins_[i][0], num_bins_[i+1][1],
  13.                              num_bins_[i][2] + num_bins_[i+1][2],
  14.                              num_bins_[i][3] + num_bins_[i+1][3])]
  15.     return num_bins_
  1. num_bins_ = num_bins.copy()
  2. afterbins = get_bin(num_bins_, 6)
  3. afterbins
  1. [(21.0, 36.0, 14797, 24809),
  2.  (36.0, 54.0, 39070, 51461),
  3.  (54.0, 61.0, 15743, 12227),
  4.  (61.0, 64.0, 6968, 3229),
  5.  (64.0, 74.0, 13376, 4206),
  6.  (74.0, 107.0, 7737, 1385)]
  1. bins_df = get_woe(afterbins)
  2. bins_df
min max count_0 count_1 total percentage bad_rate bad% good% woe
0 21.0 36.0 14797 24809 39606 0.203099 0.626395 0.254930 0.151467 -0.520618
1 36.0 54.0 39070 51461 90531 0.464242 0.568435 0.528798 0.399934 -0.279305
2 54.0 61.0 15743 12227 27970 0.143430 0.437147 0.125641 0.161151 0.248913
3 61.0 64.0 6968 3229 10197 0.052290 0.316662 0.033180 0.071327 0.765320
4 64.0 74.0 13376 4206 17582 0.090160 0.239222 0.043220 0.136922 1.153114
5 74.0 107.0 7737 1385 9122 0.046778 0.151831 0.014232 0.079199 1.716478

理想情况：每组的bad_rate差异较大，woe趋势单调

包装判断分箱个数的函数

基于卡方检验分箱：

DF：需要输入的特征数据 X：需要分箱的列名 Y：分箱数据对应的标签Y的列名 n：保留箱数 q：初始分箱数 graph：是否画出IV图像 区间为前开后闭 (]

  1. def graphforbestbin(DF, X, Y, n = 5, q = 20, graph = True):
  3.     DF = DF[[X, Y]].copy()
  5.     DF['qcut'], updown = pd.qcut(DF[X], retbins = True, q = q, duplicates = 'drop')
  7.     count_y0 = DF[DF[Y] == 0].groupby(by = 'qcut').count()[Y]
  8.     count_y1 = DF[DF[Y] == 1].groupby(by = 'qcut').count()[Y]
  9.     num_bins = [*zip(updown, updown[1:], count_y0, count_y1)]
  11.     for i in range(q):
  12.         if 0 in num_bins[0][2:]:
  13.             num_bins[0:2] = [(num_bins[0][0]
  14.                             , num_bins[1][1]
  15.                             , num_bins[0][2] + num_bins[1][2]
  16.                             , num_bins[0][3] + num_bins[1][3]
  17.                              )]
  18.             continue
  19.         for i in range(len(num_bins)):
  20.             if 0 in num_bins[i][2:]:
  21.                 num_bins[i-1:i+1] = [(num_bins[i-1][0]
  22.                                     , num_bins[i][1]
  23.                                     , num_bins[i-1][2] + num_bins[i][2]
  24.                                     , num_bins[i-1][3] + num_bins[i][3]
  25.                                      )]
  26.                 break 
  27.         else:
  28.             break
  31.     def get_woe(num_bins):
  32.         columns = ['min', 'max', 'count_0', 'count_1']
  33.         df = pd.DataFrame(num_bins, columns = columns)
  35.         df['total'] = df['count_0'] + df['count_1']
  36.         df['percentage'] = df['total']/df['total'].sum()
  38.         df['bad_rate'] = df['count_1']/df['total']
  39.         df['bad%'] = df['count_1']/df['count_1'].sum()
  40.         df['good%'] = df['count_0']/df['count_0'].sum()
  42.         df['woe'] = np.log(df['good%']/df['bad%'])
  44.         return df
  47.     def get_iv(bins_df):
  48.         rate = bins_df['good%'] - bins_df['bad%']
  49.         iv = np.sum(rate * bins_df['woe'])
  50.         return iv
  53.     IV = []
  54.     axisx = []
  56.     while len(num_bins) > n:
  57.         pvs = []
  58.         for i in range(len(num_bins) - 1):
  59.             x1 = num_bins[i][2:]
  60.             x2 = num_bins[i+1][2:]
  61.             pv = scipy.stats.chi2_contingency([x1, x2])[1]
  62.             pvs.append(pv) 
  64.         i = pvs.index(max(pvs))
  65.         num_bins[i:i+2] = [(num_bins[i][0], num_bins[i+1][1],
  66.                              num_bins[i][2] + num_bins[i+1][2],
  67.                              num_bins[i][3] + num_bins[i+1][3])]
  69.         bins_df = pd.DataFrame(get_woe(num_bins))
  70.         axisx.append(len(num_bins))
  71.         IV.append(get_iv(bins_df))
  73.     if graph:
  74.         plt.figure()
  75.         plt.plot(axisx, IV)
  76.         plt.xticks(axisx)
  77.         plt.xlabel('number of box')
  78.         plt.ylabel('IV')
  79.         plt.show()
  81.     return bins_df

不是所有的特征都可以使用这个分箱函数，如家人数量，就无法分出20组
将可以分箱的特征放出来单独分组，不能自动分箱的变量手动将其分箱

  1. # 可使用函数自动分箱的变量：
  2. auto_col_bins = {'RevolvingUtilizationOfUnsecuredLines':6,
  3.                  'age':5,
  4.                  'DebtRatio':4,
  5.                  'MonthlyIncome':3,
  6.                  'NumberOfOpenCreditLinesAndLoans':5}
  7. # 不能使用函数自动分箱的变量，手动分箱：
  8. hand_bins = {'NumberOfTime30-59DaysPastDueNotWorse':[0, 1, 2, 13],
  9.              'NumberOfTime60-89DaysPastDueNotWorse':[0, 1, 2, 17],
  10.              'NumberOfTimes90DaysLate':[0, 1, 2, 4, 54],
  11.              'NumberRealEstateLoansOrLines':[0, 1, 2, 8],
  12.              'NumberOfDependents':[0, 1, 2, 3]}
  13. # 保证区间覆盖：用负无穷表示最小值，用正无穷表示最大值
  14. hand_bins = {k:[-np.inf, *v[:-1], np.inf] for k, v in hand_bins.items()}
  1. hand_bins
  1. {'NumberOfTime30-59DaysPastDueNotWorse': [-inf, 0, 1, 2, inf],
  2.  'NumberOfTime60-89DaysPastDueNotWorse': [-inf, 0, 1, 2, inf],
  3.  'NumberOfTimes90DaysLate': [-inf, 0, 1, 2, 4, inf],
  4.  'NumberRealEstateLoansOrLines': [-inf, 0, 1, 2, inf],
  5.  'NumberOfDependents': [-inf, 0, 1, 2, inf]}
  1. bins_of_col = {}
  3. for col in auto_col_bins:
  5.     bins_df = graphforbestbin(model_data, col, 'SeriousDlqin2yrs', n = auto_col_bins[col], q = 20, graph = False)
  6.     # 返回DataFrame
  8.     bins_list = sorted(set(bins_df['min']).union(bins_df['max']))
  9.     # 返回列表
  10.     bins_list[0], bins_list[-1] = -np.inf, np.inf
  11.     # 将列表的最小值和最大值替换为无穷小和无穷大
  13.     bins_of_col[col] = bins_list
  14.     # 利用字典的性质，创建键并赋值
  16.     bins_of_col.update(hand_bins)
  1. bins_df
min max count_0 count_1 total percentage bad_rate bad% good% woe
0 0.0 1.0 3393 7823 11216 0.057516 0.697486 0.080387 0.034732 -0.839189
1 1.0 3.0 9995 13892 23887 0.122492 0.581572 0.142750 0.102312 -0.333064
2 3.0 5.0 16106 17014 33120 0.169839 0.513708 0.174831 0.164867 -0.058680
3 5.0 17.0 62732 55163 117895 0.604565 0.467899 0.566838 0.642147 0.124744
4 17.0 57.0 5465 3425 8890 0.045588 0.385264 0.035194 0.055942 0.463427 
  1. bins_list
  1. [-inf, 1.0, 3.0, 5.0, 17.0, inf]
  1. len(bins_of_col)
  1. 10
  1. bins_of_col
  1. {'RevolvingUtilizationOfUnsecuredLines': [-inf,
  2.   0.09901938874999999,
  3.   0.2977106203246584,
  4.   0.46504505549999997,
  5.   0.9823017611053088,
  6.   0.9999998999999999,
  7.   inf],
  8.  'NumberOfTime30-59DaysPastDueNotWorse': [-inf, 0, 1, 2, inf],
  9.  'NumberOfTime60-89DaysPastDueNotWorse': [-inf, 0, 1, 2, inf],
  10.  'NumberOfTimes90DaysLate': [-inf, 0, 1, 2, 4, inf],
  11.  'NumberRealEstateLoansOrLines': [-inf, 0, 1, 2, inf],
  12.  'NumberOfDependents': [-inf, 0, 1, 2, inf],
  13.  'age': [-inf, 36.0, 54.0, 61.0, 74.0, inf],
  14.  'DebtRatio': [-inf,
  15.   0.017443254267870807,
  16.   0.3205640818,
  17.   1.4677944020167184,
  18.   inf],
  19.  'MonthlyIncome': [-inf, 0.10442453781397015, 6906.041317550067, inf],
  20.  'NumberOfOpenCreditLinesAndLoans': [-inf, 1.0, 3.0, 5.0, 17.0, inf]}

映射数据

计算各箱的WOE值，并映射到数据中

  1. data = model_data.copy()
  2. data = data[['age', 'SeriousDlqin2yrs']].copy()
  3. ['cut'] = pd.cut(data['age'], [-np.inf, 36.0, 54.0, 61.0, 74.0, np.inf])
  1. data.groupby('cut').size()
  1. cut
  2. (-inf, 36.0]    39606
  3. (36.0, 54.0]    90531
  4. (54.0, 61.0]    27970
  5. (61.0, 74.0]    27779
  6. (74.0, inf]      9122
  7. dtype: int64
  1. data.groupby('cut')['SeriousDlqin2yrs'].size()
  1. cut
  2. (-inf, 36.0]    39606
  3. (36.0, 54.0]    90531
  4. (54.0, 61.0]    27970
  5. (61.0, 74.0]    27779
  6. (74.0, inf]      9122
  7. Name: SeriousDlqin2yrs, dtype: int64
  1. data.groupby('cut')['SeriousDlqin2yrs'].value_counts()
  1. cut           SeriousDlqin2yrs
  2. (-inf, 36.0]  1                   24809
  3.               0                   14797
  4. (36.0, 54.0]  1                   51461
  5.               0                   39070
  6. (54.0, 61.0]  0                   15743
  7.               1                   12227
  8. (61.0, 74.0]  0                   20344
  9.               1                    7435
  10. (74.0, inf]   0                    7737
  11.               1                    1385
  12. Name: SeriousDlqin2yrs, dtype: int64
  1. data.groupby('cut')['SeriousDlqin2yrs'].value_counts().unstack()
SeriousDlqin2yrs 0 1
cut
(-inf, 36.0] 14797 24809
(36.0, 54.0] 39070 51461
(54.0, 61.0] 15743 12227
(61.0, 74.0] 20344 7435
(74.0, inf] 7737 1385 
  1. bins_df = data.groupby('cut')['SeriousDlqin2yrs'].value_counts().unstack()
  2. bins_df['woe'] = np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum()))
  1. bins_df
SeriousDlqin2yrs 0 1 woe
cut
(-inf, 36.0] 14797 24809 -0.520618
(36.0, 54.0] 39070 51461 -0.279305
(54.0, 61.0] 15743 12227 0.248913
(61.0, 74.0] 20344 7435 1.002752
(74.0, inf] 7737 1385 1.716478 
  1. def get_woe(df, col, y, bins):
  2.     df = df[[col, y]].copy()
  3.     df['cut'] = pd.cut(df[col], bins)
  4.     bins_df = df.groupby('cut')[y].value_counts().unstack()
  5.     bins_df['woe'] = np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum()))
  6.     return bins_df['woe']
  8. woeall = {}
  9. for col in bins_of_col:
  10.     woeall[col] = get_woe(model_data, col, 'SeriousDlqin2yrs', bins_of_col[col])
  1. model_woe = pd.DataFrame(index = model_data.index)
  2. model_woe['age'] = pd.cut(model_data['age'], bins_of_col['age']).map(woeall['age'])
  1. woeall['age']
  1. cut
  2. (-inf, 36.0]   -0.520618
  3. (36.0, 54.0]   -0.279305
  4. (54.0, 61.0]    0.248913
  5. (61.0, 74.0]    1.002752
  6. (74.0, inf]     1.716478
  7. Name: woe, dtype: float64
  1. model_woe.head()
age
0 -0.279305
1 1.002752
2 -0.279305
3 1.002752
4 -0.279305 
  1. for col in bins_of_col:
  2.     model_woe[col] = pd.cut(model_data[col], bins_of_col[col]).map(woeall[col])
  3. model_woe.head()
age RevolvingUtilizationOfUnsecuredLines NumberOfTime30-59DaysPastDueNotWorse NumberOfTime60-89DaysPastDueNotWorse NumberOfTimes90DaysLate NumberRealEstateLoansOrLines NumberOfDependents DebtRatio MonthlyIncome NumberOfOpenCreditLinesAndLoans
0 -0.279305 2.200291 0.353540 0.124668 0.234166 -0.393347 0.660019 0.072859 -0.195934 -0.058680
1 1.002752 0.667595 0.353540 0.124668 0.234166 -0.393347 0.660019 0.072859 -0.195934 -0.058680
2 -0.279305 -2.037728 -0.873869 -1.769915 -1.755182 -0.393347 -0.479114 -0.313585 -0.195934 -0.058680
3 1.002752 2.200291 0.353540 0.124668 0.234166 0.614648 0.660019 -0.313585 -0.195934 0.124744
4 -0.279305 -1.073972 0.353540 0.124668 0.234166 0.614648 -0.512452 -0.313585 0.311098 0.124744 
  1. model_woe['SeriousDlqin2yrs'] = model_data['SeriousDlqin2yrs']
  1. model_woe.head()
age RevolvingUtilizationOfUnsecuredLines NumberOfTime30-59DaysPastDueNotWorse NumberOfTime60-89DaysPastDueNotWorse NumberOfTimes90DaysLate NumberRealEstateLoansOrLines NumberOfDependents DebtRatio MonthlyIncome NumberOfOpenCreditLinesAndLoans SeriousDlqin2yrs
0 -0.279305 2.200291 0.353540 0.124668 0.234166 -0.393347 0.660019 0.072859 -0.195934 -0.058680 0
1 1.002752 0.667595 0.353540 0.124668 0.234166 -0.393347 0.660019 0.072859 -0.195934 -0.058680 0
2 -0.279305 -2.037728 -0.873869 -1.769915 -1.755182 -0.393347 -0.479114 -0.313585 -0.195934 -0.058680 1
3 1.002752 2.200291 0.353540 0.124668 0.234166 0.614648 0.660019 -0.313585 -0.195934 0.124744 0
4 -0.279305 -1.073972 0.353540 0.124668 0.234166 0.614648 -0.512452 -0.313585 0.311098 0.124744 1

建模与模型验证

用准确率和ROC曲线验证模型的预测能力和捕捉能力

  1. vali_woe = pd.DataFrame(index = vali_data.index)
  3. for col in bins_of_col:
  4.     vali_woe[col] = pd.cut(vali_data[col], bins_of_col[col]).map(woeall[col])
  5. vali_woe['SeriousDlqin2yrs'] = vali_data['SeriousDlqin2yrs']
  6. vali_woe.head()
RevolvingUtilizationOfUnsecuredLines NumberOfTime30-59DaysPastDueNotWorse NumberOfTime60-89DaysPastDueNotWorse NumberOfTimes90DaysLate NumberRealEstateLoansOrLines NumberOfDependents age DebtRatio MonthlyIncome NumberOfOpenCreditLinesAndLoans SeriousDlqin2yrs
0 2.200291 0.35354 0.124668 0.234166 -0.393347 0.660019 0.248913 1.513332 -0.195934 -0.058680 0
1 -1.073972 0.35354 0.124668 0.234166 0.614648 -0.479114 -0.279305 0.072859 0.311098 0.124744 1
2 2.200291 0.35354 0.124668 0.234166 -0.393347 0.660019 1.002752 0.072859 -0.195934 -0.058680 0
3 2.200291 0.35354 0.124668 0.234166 0.195778 0.660019 -0.279305 0.072859 -0.195934 0.124744 0
4 -1.073972 0.35354 0.124668 0.234166 -0.393347 -0.512452 -0.279305 -0.313585 -0.195934 0.124744 1 
  1. vali_x = vali_woe.iloc[:, :-1]
  2. vali_y = vali_woe.iloc[:, -1]
  4. x = model_woe.iloc[:, :-1]
  5. y = model_woe.iloc[:, -1]
  1. lr = LR().fit(x, y)
  2. lr.score(x, y)
  1. 0.7857421234000657
  1. lr.score(vali_x, vali_y)
  1. 0.7651957499760697
  1. c = np.linspace(0.01, 1, 20)
  2. score = []
  4. for i in c:
  5.     lr = LR(solver = 'liblinear', C = i).fit(x, y)
  6.     score.append(lr.score(vali_x, vali_y))
  8. print(lr.n_iter_)
  9. plt.figure()
  10. plt.plot(c, score)
  1. [5]
  7. [<matplotlib.lines.Line2D at 0x26224266b00>]

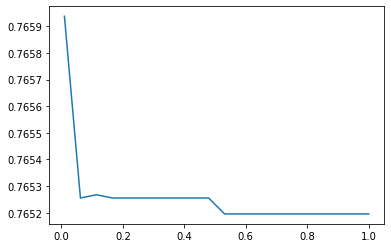
output_167_2.png

  1. score = []
  2. for i in [1, 2, 3, 4, 5, 6]: 
  3.     lr = LR(solver = 'liblinear', C = 0.025, max_iter = i).fit(x, y)
  4.     score.append(lr.score(vali_x, vali_y))
  5. plt.figure()
  6. plt.plot([1, 2, 3, 4, 5, 6], score)
  7. plt.show()
  1. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  2.   "the number of iterations.", ConvergenceWarning)
  3. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  4.   "the number of iterations.", ConvergenceWarning)
  5. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  6.   "the number of iterations.", ConvergenceWarning)
  7. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  8.   "the number of iterations.", ConvergenceWarning)
  9. C:\anaconda\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  10.   "the number of iterations.", ConvergenceWarning)

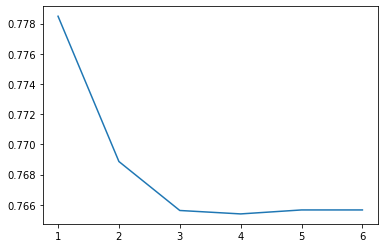
output_168_1.png

准确率较低。再来看模型在ROC曲线上的结果：

  1. import scikitplot as skplt
  2. vali_proba_df = pd.DataFrame(lr.predict_proba(vali_x))
  3. skplt.metrics.plot_roc(vali_y, vali_proba_df, 
  4.                        plot_micro = False, figsize = (6, 6),
  5.                        plot_macro = False)
  1. <matplotlib.axes._subplots.AxesSubplot at 0x2620dad42b0>

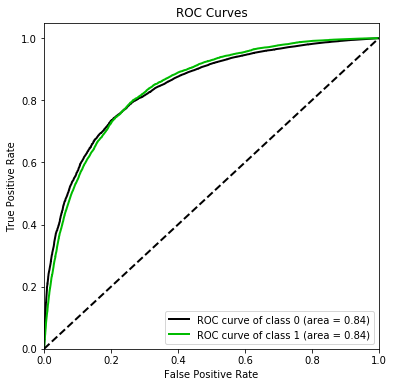
output_170_1.png

制作评分卡

逻辑回归和信用评分卡 - 图20 其中，A和B是常数，A为“补偿”，B为“刻度”，逻辑回归和信用评分卡 - 图21即对数几率，会得到逻辑回归和信用评分卡 - 图22，即参数逻辑回归和信用评分卡 - 图23特征矩阵，代表一个人的违约可能性

两个常数可以通过两个假设的分值代入公式求出：

  1. 某个特定的违约概率下的预期分值
  2. 指定的违约概率翻倍的分值(PDO)
    例如，假设对数几率为逻辑回归和信用评分卡 - 图24时，分值为600，PDO为20，即对数几率为逻辑回归和信用评分卡 - 图25时的分数为620，代入以上线性表达式可以得到：
    逻辑回归和信用评分卡 - 图26
    逻辑回归和信用评分卡 - 图27
    求出A和B，分数就很容易得到了。其中不受评分卡各特征影响的基础分，就是将截距作为逻辑回归和信用评分卡 - 图28代入公式计算，而其他各个特征的各个分档的分值，也是将系数代入计算得出：
  1. B = 20/np.log(2)
  2. A = 600 + B * np.log(1/60)
  4. base_score = A - B * lr.intercept_
  5. score_age = woeall['age'] * (-B * lr.coef_[0][1])
  1. base_score
  1. array([481.96632407])
  1. score_age
  1. cut
  2. (-inf, 36.0]   -11.323029
  3. (36.0, 54.0]    -6.074667
  4. (54.0, 61.0]     5.413673
  5. (61.0, 74.0]    21.809064
  6. (74.0, inf]     37.332055
  7. Name: woe, dtype: float64
  1. file = 'ScoreData.csv'
  3. with open(file, 'w') as fdata:
  4.     fdata.write('base_score, {}\n'.format(base_score))
  5. for i, col in enumerate(x.columns):
  6.     score = woeall[col] * (-B * lr.coef_[0][i])
  7.     score.name = "Score"
  8.     score.index.name = col
  9.     score.to_csv(file, header = True, mode = 'a')
  1. x.columns
  1. Index(['age', 'RevolvingUtilizationOfUnsecuredLines',
  2.        'NumberOfTime30-59DaysPastDueNotWorse',
  3.        'NumberOfTime60-89DaysPastDueNotWorse', 'NumberOfTimes90DaysLate',
  4.        'NumberRealEstateLoansOrLines', 'NumberOfDependents', 'DebtRatio',
  5.        'MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans'],
  6.       dtype='object')