概述
回归是一种应用广泛的预测建模技术,这种技术的核心在于预测的结果是连续型变量。
决策树,随机森林,支持向量机的分类器等分类算法的预测标签是分类变量,多以{0,1}来表示,而无监督学习算法比如PCA,KMeans并不求解标签,注意加以区别。
回归算法源于统计学理论,可能是机器学习算法中产生最早的算法之一,在现实中的应用非常广泛,包括使用其他经济指标预测股票市场指数,根据喷射流的特征预测区域内的降水量,根据公司的广告花费预测总销售额,或者根据有机物质中残留的碳-14的量来估计化石的年龄等等,只要是基于特征预测连续型变量的需求,都可以使用回归技术。
线性回归
通常来说,统计学注重先验,而机器学习看重结果,因此机器学习中不会提前为 线性回归 排除 共线性 等可能会影响模型的因素,反而会先建立模型以查看效果。模型确立之后,如果效果不好,就根据统计学的指导来排除可能影响模型的因素。
回归需求在现实中非常多,所以有各种各样的回归类算法:
- 线性回归
- 逻辑回归
- 衍生而出的岭回归,Lasso,弹性网等
- 由分类算法改进的回归
- 回归树
- 随机森林的回归
- 支持向量回归
- 贝叶斯回归
- 鲁棒的回归
- RANSAC
- Theil-Sen估计
- 胡贝尔回归
回归类算法的数学相对简单,通常,理解线性回归可以有两种角度:矩阵的角度和代数的角度。几乎所有机器学习的教材都是从代数的角度来理解线性回归的,将求解参数的问题转化为一个带条件的最优化问题,然后借助三维图像理解求极值的过程。但以下将使用矩阵方式展现回归。
sklearnt中的线性回归
sklearn中的线性模型模块是linear_model,包含了多种多样的类和函数。
多元线性回归 Linear Regression
多元线性回归的基本原理
线性回归是机器学习中最简单的回归算法,多元线性回归指的就是一个样本有多个特征的线性回归问题。对于一个有个特征的样本而言,它的回归结果可以写作方程: 被统称为模型的参数,其中
被称为截距(intercept),
~
被称为回归系数(regression coefficient),有时也用
或者
来表示。这个表达式,其实就和
是同样的性质。其中
是目标变量,也就是标签。
~
是样本上的不同特征。
如果考虑我们有m个样本,则回归结果可以被写作:
其中 是包含了m个全部的样本的回归结果的列向量。
通常使用粗体的小写字母来表示列向量,粗体的大写字母表示矩阵或者行列式。
用矩阵来表示这个方程,其中 可以被看做是一个结构为(n+1,1)的列矩阵,
是一个结构为(m,n+1)的特征矩阵,则有:
即: 从第二列到最后一列代表的是n个特征,从第一行到最后一行表示一共有m个样本。
线性回归的任务,就是构造一个预测函数来映射输入的特征矩阵 和标签值
的线性关系。预测函数的本质就是需要构建的模型,而构造预测函数的核心就是找出模型的参数向量
。因此,问题就转换为求解出参数向量。
在逻辑回归和SVM中,都是先定义了损失函数,然后通过最小化损失函数或损失函数的某种变化来将求解参数向量,以此将单纯的求解问题转化为一个最优化问题。在多元线性回归中,损失函数如下定义:
其中 是样本 i 对应的真实标签,
也就是
是样本 i 在一组参数
下的预测标签。
首先,这个损失函数代表了向量
的L2范式的平方结果,L2范式的本质是就是欧式距离,即是两个向量上的每个点对应相减后的平方和再开平方。现在只实现了向量上每个点对应相减后的平方和,并没有开方,所以损失函数是L2范式的平方结果。
在这个平方结果下,
和
分别是真实标签和预测值,也就是说,这个损失函数实在计算真实标签和预测值之间的距离。因此,这个损失函数衡量了构造的模型的预测结果和真实标签的差异,我们希望预测结果和真实值差异越小越好,所以求解目标就可以转化成:
其中右下角的2表示向量 的L2范式。在L2范式上开平方,就是我们的损失函数。这个式子,也正是sklearn当中,类
Linear_model.LinerRegression 使用的损失函数。这个式子被称为 SSE (Sum of Sqaured Error,误差平方和)或者 RSS (Residual Sum of Squares 残差平方和)。
最小二乘法求解多元线性回归的参数
现在问题转换成了求解让RSS最小化的参数向量 ,这种通过最小化真实值和预测值之间的RSS来求解参数的方法叫
做
最小二乘法。求解极值的第一步往往是求解一阶导数并让一阶导数等于0。因此,我们现在残差平方和RSS上对参数向量 求导,这里使用的矩阵求导不同于代数求导:
令一阶导数为0:
在这里,逆矩阵存在的充分必要条件是特征矩阵没有 **多重共线性** 。假设矩阵的逆是存在的,此时的 就是参数的最优解。解出这个参数向量,就解出了
,也就是预测值
。在sklearn中,矩阵使用奇异值分解来求解。
在统计学中,使用最小二乘法来求解线性回归的方法是一种“无偏估计”的方法,这种无偏估计要求因变量,也就是标签的分布必须服从正态分布。 必须经由正态化处理(比如说取对数,或者使用类
QuantileTransformer 或者 PowerTransformer )。但在机器学习中会先考虑模型的效果,如果模型效果不好,再考虑改变因变量的分布。
linear_model.LinearRegression
class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
| 参数 | 含义 |
|---|---|
| fit_intercept | 布尔值,可不填,默认为True |
是否计算此模型的截距。如果设置为False,则不会计算截距 |
| normalize | 布尔值,可不填,默认为False
当fit_intercept设置为False时,将忽略此参数。如果为True,则特征矩阵X在进入回归之前将会被减去均值(中心化)并除以L2范式(缩放)。如果希望进行标准化,在fit数据之前使用preprocessing模块中的标准化专用类StandardScaler |
| copy_X | 布尔值,可不填,默认为True
如果为真,将在X.copy()上进行操作,否则的话原本的特征矩阵X可能被线性回归影响并覆盖 |
| n_jobs | 整数或者None,可不填,默认为None
用于计算的作业数。只在多标签的回归和数据量足够大的时候才生效。除非None在
joblib.parallel_backend上下文中,否则None统一表示为1。如果输入 -1,则表示使用全部的CPU来进行计算 |
线性回归的类的优点是简单,仅有四个参数就可以完成一个完整的算法,而且这些参数中没有一个是必填的,且没有一个是数值型,这说明,线性回归的性能往往取决于数据本身,而并非是调参。因此线性回归对数据有着很高的要求。幸运的是,现实中很多连续型变量之间,都存在着或多或少的线性联系。所以线性回归虽然简单,却很强大。
此外,sklearn中的线性回归可以处理多标签问题,只需要在fit的时候输入多维度标签就可以了。
1. 导入需要的模块和库
from sklearn.linear_model import LinearRegression as LRfrom sklearn.model_selection import train_test_splitfrom sklearn.model_selection import cross_val_scorefrom sklearn.datasets import fetch_california_housing as fch # 加利福尼亚房屋价值数据集import pandas as pd
2. 导入数据,探索数据
housevalue = fch() # 数据集实例化,需要下载
Downloading Cal. housing from https://ndownloader.figshare.com/files/5976036 to C:\Users\chenh\scikit_learn_data
housevalue
{'data': array([[ 8.3252 , 41. , 6.98412698, ..., 2.55555556,37.88 , -122.23 ],[ 8.3014 , 21. , 6.23813708, ..., 2.10984183,37.86 , -122.22 ],[ 7.2574 , 52. , 8.28813559, ..., 2.80225989,37.85 , -122.24 ],...,[ 1.7 , 17. , 5.20554273, ..., 2.3256351 ,39.43 , -121.22 ],[ 1.8672 , 18. , 5.32951289, ..., 2.12320917,39.43 , -121.32 ],[ 2.3886 , 16. , 5.25471698, ..., 2.61698113,39.37 , -121.24 ]]),'target': array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894]),'feature_names': ['MedInc','HouseAge','AveRooms','AveBedrms','Population','AveOccup','Latitude','Longitude'],'DESCR': '.. _california_housing_dataset:\n\nCalifornia Housing dataset\n--------------------------\n\n**Data Set Characteristics:**\n\n :Number of Instances: 20640\n\n :Number of Attributes: 8 numeric, predictive attributes and the target\n\n :Attribute Information:\n - MedInc median income in block\n - HouseAge median house age in block\n - AveRooms average number of rooms\n - AveBedrms average number of bedrooms\n - Population block population\n - AveOccup average house occupancy\n - Latitude house block latitude\n - Longitude house block longitude\n\n :Missing Attribute Values: None\n\nThis dataset was obtained from the StatLib repository.\nhttp://lib.stat.cmu.edu/datasets/\n\nThe target variable is the median house value for California districts.\n\nThis dataset was derived from the 1990 U.S. census, using one row per census\nblock group. A block group is the smallest geographical unit for which the U.S.\nCensus Bureau publishes sample data (a block group typically has a population\nof 600 to 3,000 people).\n\nIt can be downloaded/loaded using the\n:func:`sklearn.datasets.fetch_california_housing` function.\n\n.. topic:: References\n\n - Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,\n Statistics and Probability Letters, 33 (1997) 291-297\n'}
type(housevalue)
sklearn.utils.Bunch
housevalue.data
array([[ 8.3252 , 41. , 6.98412698, ..., 2.55555556,37.88 , -122.23 ],[ 8.3014 , 21. , 6.23813708, ..., 2.10984183,37.86 , -122.22 ],[ 7.2574 , 52. , 8.28813559, ..., 2.80225989,37.85 , -122.24 ],...,[ 1.7 , 17. , 5.20554273, ..., 2.3256351 ,39.43 , -121.22 ],[ 1.8672 , 18. , 5.32951289, ..., 2.12320917,39.43 , -121.32 ],[ 2.3886 , 16. , 5.25471698, ..., 2.61698113,39.37 , -121.24 ]])
X = pd.DataFrame(housevalue.data, columns=housevalue.feature_names)X.head()
| MedInc | HouseAge | AveRooms | AveBedrms | Population | AveOccup | Latitude | Longitude | |
|---|---|---|---|---|---|---|---|---|
| 0 | 8.3252 | 41.0 | 6.984127 | 1.023810 | 322.0 | 2.555556 | 37.88 | -122.23 |
| 1 | 8.3014 | 21.0 | 6.238137 | 0.971880 | 2401.0 | 2.109842 | 37.86 | -122.22 |
| 2 | 7.2574 | 52.0 | 8.288136 | 1.073446 | 496.0 | 2.802260 | 37.85 | -122.24 |
| 3 | 5.6431 | 52.0 | 5.817352 | 1.073059 | 558.0 | 2.547945 | 37.85 | -122.25 |
| 4 | 3.8462 | 52.0 | 6.281853 | 1.081081 | 565.0 | 2.181467 | 37.85 | -122.25 |
MedInc:该街区住户的收入中位数
HouseAge:该街区房屋使用年代的中位数
AveRooms:该街区平均的房间数目
AveBedrms:该街区平均的卧室数目
Population:街区人口
AveOccup:平均入住率
Latitude:街区的纬度
Longitude:街区的经度
X.shape
(20640, 8)
y = housevalue.targety
array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894])
print(y.min(), y.max())
0.14999 5.00001
3. 分训练集和测试集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, y, test_size = 0.3, random_state = 420)Xtrain.head()
| MedInc | HouseAge | AveRooms | AveBedrms | Population | AveOccup | Latitude | Longitude | |
|---|---|---|---|---|---|---|---|---|
| 17073 | 4.1776 | 35.0 | 4.425172 | 1.030683 | 5380.0 | 3.368817 | 37.48 | -122.19 |
| 16956 | 5.3261 | 38.0 | 6.267516 | 1.089172 | 429.0 | 2.732484 | 37.53 | -122.30 |
| 20012 | 1.9439 | 26.0 | 5.768977 | 1.141914 | 891.0 | 2.940594 | 36.02 | -119.08 |
| 13072 | 2.5000 | 22.0 | 4.916000 | 1.012000 | 733.0 | 2.932000 | 38.57 | -121.31 |
| 8457 | 3.8250 | 34.0 | 5.036765 | 1.098039 | 1134.0 | 2.779412 | 33.91 | -118.35 |
for i in [Xtrain, Xtest]:i.index = range(i.shape[0])Xtrain.head()
| MedInc | HouseAge | AveRooms | AveBedrms | Population | AveOccup | Latitude | Longitude | |
|---|---|---|---|---|---|---|---|---|
| 0 | 4.1776 | 35.0 | 4.425172 | 1.030683 | 5380.0 | 3.368817 | 37.48 | -122.19 |
| 1 | 5.3261 | 38.0 | 6.267516 | 1.089172 | 429.0 | 2.732484 | 37.53 | -122.30 |
| 2 | 1.9439 | 26.0 | 5.768977 | 1.141914 | 891.0 | 2.940594 | 36.02 | -119.08 |
| 3 | 2.5000 | 22.0 | 4.916000 | 1.012000 | 733.0 | 2.932000 | 38.57 | -121.31 |
| 4 | 3.8250 | 34.0 | 5.036765 | 1.098039 | 1134.0 | 2.779412 | 33.91 | -118.35 |
Xtrain.shape
(14448, 8)
4. 标准化
先用训练集fit标准化的类,然后用训练好的类分别transform训练集和测试集
5. 建模
reg = LR().fit(Xtrain, Ytrain)yhat = reg.predict(Xtest)yhat
array([1.51384887, 0.46566247, 2.2567733 , ..., 2.11885803, 1.76968187,0.73219077])
print(yhat.min(), yhat.max())
-0.6528439725035966 7.146198214270875
最小值和最大值都超出了真实标签的范围,模型拟合效果较差。留到后面评估模型时再处理。
6. 探索模型
reg.coef_
array([ 4.37358931e-01, 1.02112683e-02, -1.07807216e-01, 6.26433828e-01,5.21612535e-07, -3.34850965e-03, -4.13095938e-01, -4.26210954e-01])
reg.intercept_
-36.25689322920386
分析:系数值极小,是否可通过令normalize为True来改善?
reg_nor = LR(normalize = True).fit(Xtrain, Ytrain)yhat_nor = reg_nor.predict(Xtest)yhat_nor
array([1.51384887, 0.46566247, 2.2567733 , ..., 2.11885803, 1.76968187,0.73219077])
reg_nor.coef_
array([ 4.37358931e-01, 1.02112683e-02, -1.07807216e-01, 6.26433828e-01,5.21612535e-07, -3.34850965e-03, -4.13095938e-01, -4.26210954e-01])
reg_nor.intercept_
-36.25689322920398
结论:毫无效果。系数和截距没有变化,预测值也没有改变。
[*zip(Xtrain.columns, reg.coef_)]
[('MedInc', 0.4373589305968403),('HouseAge', 0.010211268294494038),('AveRooms', -0.10780721617317715),('AveBedrms', 0.6264338275363783),('Population', 5.216125353178735e-07),('AveOccup', -0.0033485096463336094),('Latitude', -0.4130959378947711),('Longitude', -0.4262109536208467)]
print(reg.coef_.max(), reg.coef_.min())
0.6264338275363783 -0.4262109536208467
AveBedrms、MedInc、Longitude和Latitude是最重要的系数,而Population是最不重要的系数
| 属性 | 含义 |
|---|---|
| coef_ 即参数向量 |
数组,形状为 (n_features, )或者(n_targets, n_features) |
线性回归方程中估计出的系数。如果在fit中传递多个标签(当y为二维或以上的时候),则返回 的系数是形状为(ntargets,n_features)的二维数组,而如果仅传递一个标签,则返回的系 数是长度为n_features的一维数组 | | intercept | 数组,线性回归中的截距项 |
回归类的模型评估指标
比起准确率这种容易理解的指标,回归算法的评估指标更难理解,而且由于回归算法有着比分类算法更多的目的,除了拟合正确的数据之外,还希望得出数据的趋势、分布以及数据间的相关性等不能用数值直接表达的信息,所以回归算法的评估指标也更加复杂。
不像无监督学习算法中的轮廓系数等等评估指标,回归类与分类型算法的模型评估其实是相似的法则——找真实标签和预测值的差异。只不过在分类型算法中,这个差异只有一种角度来评判,那就是是否预测到了正确的分类,比如0或1。而在回归类算法中,有两种不同的角度来看待回归的效果:
第一,是否预测到了正确的数值。
第二,是否拟合到了足够的信息。比如,5.3的前面是3,后面是6.1,是否预测到了(3, 5.3, 6,1)这样的趋势。
这两种角度,分别对应着不同的模型评估指标。
是否预测了正确的数值?
RSS残差平方和的本质是预测值与真实值之间的差异,也就是从第一种角度来评估回归的效力,所以RSS既是损失函数,也是回归类模型的模型评估指标之一:
但是,RSS有着致命的缺点:
它是一个无界的和,可以无限地大。我们想求解最小的RSS,从RSS的公式来看,它不能为负,所以RSS越接近0越好,但没有一个概念关于多小才算好,多接近0才算好。
为了应对这种状况,sklearn中使用RSS的变体,均方误差MSE(mean squared error)来衡量预测值和真实值的差异:
均方误差的本质是在RSS的基础上除以了样本总量,得到了每个样本量上的平均误差。有了平均误差,就可以将平均误差和标签的取值范围放在一起比较,以此获得一个较为可靠的评估依据。
在sklearn当中,有两种方式调用这个评估指标:
- 使用sklearn专用的模型评估模块metrics里的类mean_squared_error;
- 调用交叉验证的类cross_val_score并使用里面的scoring参数来设置使用均方误差。
from sklearn.metrics import mean_squared_error as MSEMSE(yhat, Ytest)
0.5309012639324571
Ytest.mean()
2.0819292877906976
所以0.5的MSE对于此次的回归模型来说,是一个比较大的值,难以接受。而且模型预测出的最大值和最小值都超出数据范围很多。
cross_val_score(reg, X, y, cv = 10, scoring = 'neg_mean_squared_error')
array([-0.48922052, -0.43335865, -0.8864377 , -0.39091641, -0.7479731 ,-0.52980278, -0.28798456, -0.77326441, -0.64305557, -0.3275106 ])
cross_val_score(reg, X, y, cv = 10, scoring = 'neg_mean_squared_error') * -1
array([0.48922052, 0.43335865, 0.8864377 , 0.39091641, 0.7479731 ,0.52980278, 0.28798456, 0.77326441, 0.64305557, 0.3275106 ])
cross_val_score(reg, X, y, cv = 10, scoring = 'neg_mean_squared_error').mean()
-0.550952429695658
import sklearnsorted(sklearn.metrics.SCORERS.keys())
['accuracy','adjusted_mutual_info_score','adjusted_rand_score','average_precision','balanced_accuracy','completeness_score','explained_variance','f1','f1_macro','f1_micro','f1_samples','f1_weighted','fowlkes_mallows_score','homogeneity_score','jaccard','jaccard_macro','jaccard_micro','jaccard_samples','jaccard_weighted','max_error','mutual_info_score','neg_brier_score','neg_log_loss','neg_mean_absolute_error','neg_mean_gamma_deviance','neg_mean_poisson_deviance','neg_mean_squared_error','neg_mean_squared_log_error','neg_median_absolute_error','neg_root_mean_squared_error','normalized_mutual_info_score','precision','precision_macro','precision_micro','precision_samples','precision_weighted','r2','recall','recall_macro','recall_micro','recall_samples','recall_weighted','roc_auc','roc_auc_ovo','roc_auc_ovo_weighted','roc_auc_ovr','roc_auc_ovr_weighted','v_measure_score']
均方误差为负
虽然均方误差永远为正,但是sklearn中的参数scoring下,均方误差作为评判标准时,却是计算“负均方误差”(negmean_squared_error)的。这是因为sklearn在计算模型评估指标的时候,会考虑指标本身的性质,均方误差本身是一种误差,所以被sklearn划分为模型的一种损失(loss)。在sklearn当中,所有的损失都使用负数表示,因此均方误差也被显示为负数了。真正的均方误差MSE,其实就是 neg_mean_squared_error 去掉负号。
除了MSE,还有与MSE类似的MAE(Mean absolute error,绝对均值误差):

是否拟合了足够的信息?
对于回归类算法而言,只探索数据预测是否准确是不足够的。除了数据本身的数值大小之外,我们还希望模型
能够捕捉到数据的“规律”,比如数据的分布规律,单调性等等,而是否捕获了这些信息并无法使用MSE来衡量。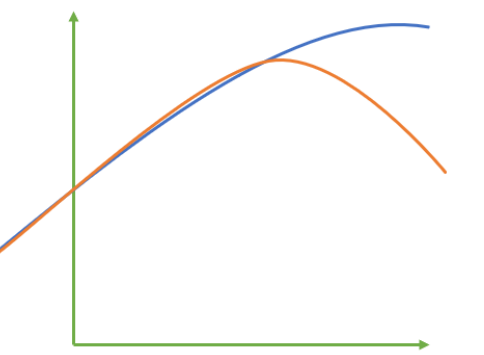
上图红色线是真实标签,而蓝色线是拟合模型。这是一种比较极端,但的确可能发生的情况。这张图像上,前半部分的拟合非常成功,看上去真实标签和预测结果几乎重合,但后半部分的拟合却非常糟糕,模型向着与真实标签完全相反的方向去了。
对于这样的一个拟合模型,如果使用MSE来对它进行判断,它的MSE会很小,因为大部分样本其实都被完美拟合了,少数样本的真实值和预测值的巨大差异在被均分到每个样本上之后。但这样的拟合结果必然不是一个好结果,因为一旦新样本是处于拟合曲线的后半段的,预测结果必然会有巨大的偏差。
所以,指标除了判断预测数值是否正确之外,还要能够判断模型是否拟合了足够多的,数值之外的信息。降维算法PCA使用方差来衡量数据上的信息量。如果方差越大,代表数据上的信息量越多,而这个信息量不仅包括了数值的大小,还包括了我们希望模型捕捉的那些规律。为了衡量模型对数据上的信息量的捕捉,定义:
其中 是我们的真实标签,
是我们的预测结果,
是我们的均值,
如果除以样本量m就是方差。方差的本质是任意一个y值和样本均值的差异,差异越大,这些值所带的信息越多。在
中,分子是真实值和预测值之差的
差值,也就是模型没有捕获到的信息总量,分母是真实标签所带的信息量,相当于:
所以,越接近1越好。
可以使用三种方式来调用:
- 直接从metrics中导入r2_score,输入预测值和真实值后打分;
直接从线性回归LinearRegression的接口score来进行调用;
回归类算法的score接口默认使用
在交叉验证中,输入
r2来调用。
r2 = reg.score(Xtest, Ytest)r2
0.6043668160178817
相同的评估指标不同的结果
from sklearn.metrics import r2_scorer2_score(yhat, Ytest)
0.33806537615560006
为什么相同的评估指标会有不同的结果?
r2_score(Ytest, yhat)
0.6043668160178817
cross_val_score(reg, X, y, cv = 10, scoring = 'r2').mean()
0.5110068610524564
在分类模型的评价指标当中,进行的是一种 if a == b 对比,这种判断和 if b == a 完全是一种概念。然而R2明显和分类模型的指标中的accuracy或者precision不一样,R2涉及到的计算中对预测值和真实值有极大的区别,必须是预测值在分子,
真实值在分母,所以我们在调用metrcis模块中的模型评估指标的时候,使用shift tab键检查清楚,指标的参数中究竟是要求先输入真实值还是先输入预测值。也可以指定参数,就不必在意顺序了。
模型在加利福尼亚房屋价值数据集上的MSE其实不是很大(0.5),但我们的不高,这证明模型比较好地拟合了一部分数据的数值,却没有能正确拟合数据的分布。
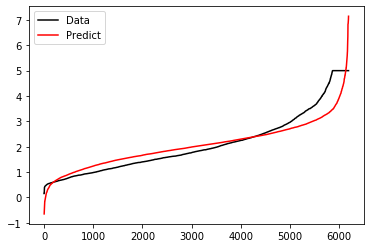
我们可以绘制一张图上的两条曲线,一条曲线是真实标签 Ytest,另一条曲线是预测结果
yhat,两条曲线的交叠越多,说明模型拟合就越好:
import matplotlib.pyplot as pltplt.plot(range(len(Ytest)), sorted(Ytest), c = 'black', label = 'Data')plt.plot(range(len(yhat)), sorted(yhat), c = 'red', label = 'Predict')plt.legend()plt.show()
在sklearn中,一个与 非常相似的指标叫做可解释性方差分数(explained_variance_score,EVS),它也是衡量
1 - 没有捕获到的信息占总信息的比例,但它和略有不同。
R为负
import numpy as nprng = np.random.RandomState(42)X = rng.randn(100, 80)y = rng.randn(100)cross_val_score(LR(), X, y, cv = 5, scoring = 'r2')
array([-179.12952605, -5.692624 , -15.61747513, -78.68042858,-59.5311006 ])
的计算公式:
是1减一个数,后面的部分只要大于1的话
完全可以小于0。
在机器学习教材中,除了RSS之外,还有解释平方和ESS(Explained Sum of Squares,也叫做SSR回归平方和)以及总离差平方和
TSS(Total Sum of Squares,也叫做SST总离差平方和)。解释平方和ESS定义了预测值和样本均值之间的差异,而总离差平方和TSS定义了真实值和样本均值之间的差异(就是中的分母)。两个指标分别写作:
且有,将其代入
公式得:
因为ESS和TSS都不为负,所以不为负。
但是, 不是永远成立的:
可推得:
当 为0时,公式
才会成立,但
衡量的是真实值到预测值的距离,而
衡量的是预测值到均值的距离,当这两个部分的符号不同的时候,
就为负,而
就可能是一个负数。
下图蓝色的横线是均值线 ,橙色的线是模型 ,蓝色的点是样本点。现在对于来说,真实标签减预测值的值
为正,但
却是一个负数,这说明,数据本身的均值,比我们对数据的拟合模型本身更接近数据的真实值,这样的模型就是没有作用的,类似于分类模型中的分类准确率为50%,不如瞎猜。
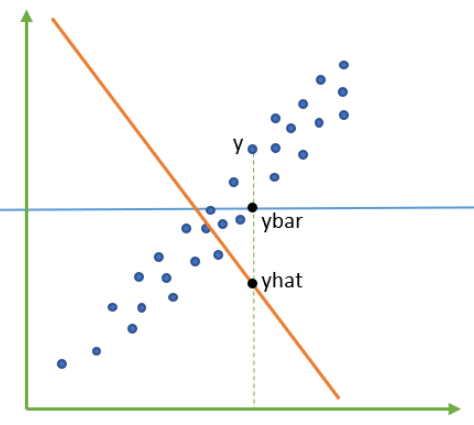
当显示为负的时候,说明模型对数据的拟合非常糟糕。
现实应用中,如果线性回归模型出现了负的,首先检查数据处理过程和建模过程是否正确,也许数据处理过程中已经伤害了数据本身(比如删除了重要特征,抽样、标准化过程有问题等等),也许建模过程存在bug,导致数据非常难拟合。如果是集成模型的回归,检查弱评估器的数量是否足够,随机森林,提升树这些模型在只有两三棵树的时候
很容易出现负的 。如果检查了代码,也确定了预处理没有问题,但
还是负的,那这就证明线性回归模型不适合这样的数据,可以尝试其他的算法,也可能是数据不存在规律。
多重共线性:岭回归 与 Lasso
岭回归与Lasso这两个算法不是为了提升模型表现,而是为了修复漏洞而设计的(实际上,使用岭回归或者Lasso时,模型的效果往往会下降一些,因为删除了一小部分信息)。
多重共线性
多元线性回归使用最小二乘法的求解原理,对多元线性回归的损失函数求导,并得出求解系数 的式子和过程:
在最后一步需要左乘 的逆矩阵,而逆矩阵存在的充分必要条件是特征矩阵不存在
多重共线性 。
【证明】
- 逆矩阵存在的充分必要条件
逆矩阵的计算公式:
分子上是伴随矩阵,任何矩阵都可以有伴随矩阵,而分母上的行列式
不能为0,一旦为0则无法计算出逆矩阵。因此逆矩阵存在的充分必要条件是:矩阵的行列式
不能为0,对于线性回归而言,即是说
不能为0。这是使用最小二乘法来求解线性回归的核心条件之一。
矩阵是一组数按一定方式排列成的数表,一般记作
行列式是一组数按某种运算法则计算出来的一个数,通常记作或者
- 行列式不为0的充分必要条件
特征矩阵
结构为(m,n),则
就是结构为(n,m)的矩阵乘以结构为(m,n)的矩阵,得到结构为(n,n)的
方阵 。
行列式计算公式: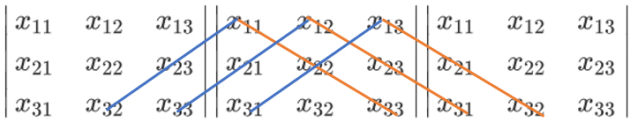
在线性代数中,可以利用行列式的性质将一个行列式整合成一个梯形的行列式:
梯形的行列式表现为所有的数字都被整合到对角线的上方或下方(通常是上方),虽然具体的数字发生了变化(比
如由变成了
),但是行列式的大小在初等行/列变换的过程中是不变的。梯形行列式计算要容易很多:
矩阵的行列式其实就是梯形行列式对角线上的元素相乘。此时,只要对角线上的任意元素为0,行列式就为0。只要对角线上没有一个元素为0,行列式就不会为0,即 满秩矩阵 。
n行n列的矩阵A转换为梯形矩阵后,没有任何全为0的行或者全为0的列,则称A为
满秩矩阵。 只要对角线上没有一个元素为0,则这个矩阵中绝对不可能存在全为0的行或列。
矩阵满秩(即转换为梯形矩阵后对角线上没有0)是矩阵的行列式不为0的充分必要条件。
- 矩阵满秩的充分必要条件
一个矩阵要满秩,则转换为梯形矩阵后的对角线上没有0。
,矩阵A不是满秩的,存在完全具有线性关系的两行。
,矩阵B满秩。虽然对角线上每个元素都不为0,但具有非常接近于0的元素
0.02。,矩阵C满秩。而且对角线上没有任何元素特别接近于0。
矩阵A中第一行和第三行的关系,被称为 精确相关关系 ,即 完全相关 ,一行可使另一行化为0。在这种精确相关关系下,矩阵A的行列式为0,则矩阵A的逆不可能存在。在最小二乘法中,如果矩阵 中存在这种精确相关关系,则对应的逆不存在,最小二乘法完全无法使用,线性回归会无法求出结果:
矩阵B中第一行和第三行的关系不太一样,他们之间非常接近于精确相关关系,但又不是完全相关,一行不能使另
一行化为0,这种关系被称为高度相关关系。在这种高度相关关系下,矩阵的行列式不为0,但是非常接近0,
矩阵的逆存在,不过接近于无限大。在这种情况下,最小二乘法可以使用,但是得到的逆会很大,直接影响对参数向量 的求解:
这样求解出来的参数向量 会很大,因此会影响建模的结果,造成模型有偏差或者不可用。精确相关关系和高度相关关系并称为
多重共线性 。在多重共线性下,模型无法建立,或者模型不可用。
矩阵C的行之间结果相互独立,梯形矩阵看起来正常,它的对角线上没有任何元素特别接近于0,因此其行列式也就不会为0或者接近0,因此矩阵C得出的参数向量 就不会有太大偏差,对于拟合而言是比较理想的:
一个矩阵如果要满秩,则要求矩阵中每个向量之间不能存在多重共线性。这也构成了线性回归算法对于特征矩阵的要求。
相关性
多重共线性如果存在,则线性回归就无法使用最小二乘法来进行求解,或者求解就会出现偏差。不能存在多重共线性,不代表不能存在相关性——机器学习不要求特征之间必须独立,必须不相关,只要不是高度相关或者精确相关就好。**多重共线性**(Multicollinearity) 与 **相关性**(Correlation)
多重共线性是一种统计现象,是指线性模型中的特征(解释变量)之间由于存在精确相关关系或高度相关关系,导致模型无法建立,或者估计失真。多重共线性使用指标方差膨胀因子(variance inflation
factor,VIF)来衡量(from statsmodels.stats.outliers_influence import variance_inflation_factor),
通常当提到“共线性”,特指多重共线性。
相关性是衡量两个或多个变量一起波动的程度的指标,它可以是正的,负的或者0。提到变量之间具有相关性,通常是指线性相关性。线性相关一般由皮尔逊相关系数进行衡量,非线性相关可以使用斯皮尔曼相关系数或
者互信息法进行衡量。
现实中特征之间完全独立的情况非常少,因为大部分数据统计手段或者收集者并不考虑统计学或者机器学习建模时的需求,数据多多少少都会存在一些 相关性 ,极端情况下,甚至还可能出现收集的特征数量比样本数量多的情况。通常来说,这些相关性在机器学习中通常无伤大雅(在统计学中可能是比较严重的问题),即便有一些偏差,只要最小二乘法能够求解即可,毕竟,想要消除特征的相关性,无论使用怎样的手段,都无法避免 特征选择 ,这意味着可用的信息变得更加少,对于机器学习来说,很有可能排除相关性后,模型的整体效果受到巨大的打击。这种情况下选择不处理相关性。
然而 多重共线性 的存在会造成模型极大地偏移,无法模拟数据的全貌,因此是必须解决的问题。为了保留线性模型计算快速,理解容易的优点,我们并不希望更换成非线性模型,这促使统计学家和机器学习研究者们钻研出了多种能够处理多重共线性的方法,其中有三种比较常见的:
| 思路 | 原理 | 特点 |
|---|---|---|
| 统计学先验 | 在开始建模之前先对数据进行各种相关性检验,如果存在多重共线性则可考虑对数据的特征进行删减筛查,或者使用降维算法对其进行处理,最终获得一个完全不存在相关性的数据集 | 耗时耗力,需要较多的人工操作,并且会需要混合各种统计学中的知识和检验。机器学习中能够一种模型解决,尽量不用多个模型,能够追求结果,尽量避免一系列检验。统计学的检验以“让特征独立”为目标,而机器学习“稍微相关也无妨” |
| 向前逐步回归 | 筛选对标签解释力度最强的特征,同时对于存在相关性的特征们加上⼀个惩罚项,削弱其对标签的贡献,以绕过最小二乘法对共线性较为敏感的缺陷 | 在现实中应用较多,不过由于理论复杂,效果也不是非常高效,因此不是首选 |
| 改进线性回归 | 在原有的线性回归算法基础上修改,使其能容忍特征列存在多重共线性,顺利建模,且尽可能的保证RSS取得最小值 | 岭回归,Lasso,弹性网 |
岭回归
岭回归解决多重共线性问题
岭回归,又称为吉洪诺夫正则化(Tikhonov regularization)。大部分的机器学习教材会使用代数的形式来展现岭回归的原理,这个原理和逻辑回归及支持向量机非常相似,都是将求解的过程转化为一个 带条件的最优化问题 ,然后用最小二乘法求解。
岭回归的原理也可以用矩阵非常简单地表达出来。岭回归在多元线性回归的损失函数上加上了正则项,表达为系数 的L2范式(即系数
的平方项)乘以正则化系数
。岭回归的损失函数的完整表达式写作:
这个简单的操作带来了巨大的变化。在线性回归中通过在损失函数上对 求导来求解极值,在这里虽然加上了正则项,依然使用最小二乘法来求解。假设我们的特征矩阵结构为(m,n),系数
的结构是(1,n),则:
令一阶导数为0,得:
显然,只要 存在逆矩阵,就可以求解出
。一个矩阵存在逆矩阵的充分必要条件是这个矩阵的行列式不为0。假设原本的特征矩阵中存在共线性,则方阵
就会不满秩(存在全为零的行),此时最小二乘法就无法使用。然而,在加上了
之后,除非:
等于0,或者
- 原本的矩阵
对角线上存在元素为
,而且其他行或者列的元素都为0
否则矩阵 永远都是满秩。在sklearn中,
的值可以控制,因此可以让它不为0,以避免第一种情况。而第二种情况,如果我们发现某个
取值下模型无法求解,只需要换一个
的取值即可。也就是说,矩阵的逆是永远存在的。有利这个保障,
就可以写作:
如此,正则化系数 就避免了
精确相关关系 带来的影响。而对于存在 高度相关关系 的矩阵,我们也可以通过调大 ,来让
的行列式变大,从而让逆矩阵变小,以此控制参数向量
的偏移。当
越大,模型越不容易受到共线性的影响:
如此,多重共线性就被控制住了:最小二乘法一定有解,并且这个解可以通过 来进行调节,以确保不会偏离太多。当然了,
挤占了
中由原始的特征矩阵贡献的空间,因此如果
太大,也会导致
的估计出现较大的偏移,无法正确拟合数据的真实面貌。使用中,需要找出让模型效果变好的最佳
取值。
linear_model.Ridge
class sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None,
tol=0.001, solver=’auto’, random_state=None)
和线性回归相比,岭回归的参数略多,但是核心参数就是正则项的系数 ,其他的参数是当使用最小二乘法之外的方法求解岭回归的时候才需要的,通常不需要去触碰这些参数。
前面在加利佛尼亚房屋价值数据集上使用线性回归,得出的结果是训练集上的拟合程度是60%,测试集上的拟合程度也是60%左右,那这个很低的是不是由多重共线性造成的呢?
在统计学中会通过 VIF 或者各种检验来判断数据是否存在共线性,然而在机器学习中,使用模型来判断——如果一个数据集在岭回归中使用各种正则化参数取值下模型表现没有明显上升(比如出现持平或者下降),则说明数据没有多重共线性,顶多是特
征之间有一些相关性。反之,如果一个数据集在岭回归的各种正则化参数取值下表现出明显的上升趋势,则说明数据存在多重共线性。
import numpy as npimport pandas as pdfrom sklearn.linear_model import Ridge, LinearRegression, Lassofrom sklearn.model_selection import train_test_split as TTSfrom sklearn.datasets import fetch_california_housing as fchimport matplotlib.pyplot as plt
housevalue = fch()X = pd.DataFrame(housevalue.data)y = pd.DataFrame(housevalue.target)
X.head()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 8.3252 | 41.0 | 6.984127 | 1.023810 | 322.0 | 2.555556 | 37.88 | -122.23 |
| 1 | 8.3014 | 21.0 | 6.238137 | 0.971880 | 2401.0 | 2.109842 | 37.86 | -122.22 |
| 2 | 7.2574 | 52.0 | 8.288136 | 1.073446 | 496.0 | 2.802260 | 37.85 | -122.24 |
| 3 | 5.6431 | 52.0 | 5.817352 | 1.073059 | 558.0 | 2.547945 | 37.85 | -122.25 |
| 4 | 3.8462 | 52.0 | 6.281853 | 1.081081 | 565.0 | 2.181467 | 37.85 | -122.25 |
y.head()
| 0 | |
|---|---|
| 0 | 4.526 |
| 1 | 3.585 |
| 2 | 3.521 |
| 3 | 3.413 |
| 4 | 3.422 |
X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目","平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]X.head()
| 住户收入中位数 | 房屋使用年代中位数 | 平均房间数目 | 平均卧室数目 | 街区人口 | 平均入住率 | 街区的纬度 | 街区的经度 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 8.3252 | 41.0 | 6.984127 | 1.023810 | 322.0 | 2.555556 | 37.88 | -122.23 |
| 1 | 8.3014 | 21.0 | 6.238137 | 0.971880 | 2401.0 | 2.109842 | 37.86 | -122.22 |
| 2 | 7.2574 | 52.0 | 8.288136 | 1.073446 | 496.0 | 2.802260 | 37.85 | -122.24 |
| 3 | 5.6431 | 52.0 | 5.817352 | 1.073059 | 558.0 | 2.547945 | 37.85 | -122.25 |
| 4 | 3.8462 | 52.0 | 6.281853 | 1.081081 | 565.0 | 2.181467 | 37.85 | -122.25 |
Xtrain, Xtest, Ytrain, Ytest = TTS(X, y, test_size = 0.3, random_state = 420)Xtrain.head()
| 住户收入中位数 | 房屋使用年代中位数 | 平均房间数目 | 平均卧室数目 | 街区人口 | 平均入住率 | 街区的纬度 | 街区的经度 | |
|---|---|---|---|---|---|---|---|---|
| 17073 | 4.1776 | 35.0 | 4.425172 | 1.030683 | 5380.0 | 3.368817 | 37.48 | -122.19 |
| 16956 | 5.3261 | 38.0 | 6.267516 | 1.089172 | 429.0 | 2.732484 | 37.53 | -122.30 |
| 20012 | 1.9439 | 26.0 | 5.768977 | 1.141914 | 891.0 | 2.940594 | 36.02 | -119.08 |
| 13072 | 2.5000 | 22.0 | 4.916000 | 1.012000 | 733.0 | 2.932000 | 38.57 | -121.31 |
| 8457 | 3.8250 | 34.0 | 5.036765 | 1.098039 | 1134.0 | 2.779412 | 33.91 | -118.35 |
for i in [Xtrain, Xtest]:i.index = range(i.shape[0])Xtrain.head()
| 住户收入中位数 | 房屋使用年代中位数 | 平均房间数目 | 平均卧室数目 | 街区人口 | 平均入住率 | 街区的纬度 | 街区的经度 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 4.1776 | 35.0 | 4.425172 | 1.030683 | 5380.0 | 3.368817 | 37.48 | -122.19 |
| 1 | 5.3261 | 38.0 | 6.267516 | 1.089172 | 429.0 | 2.732484 | 37.53 | -122.30 |
| 2 | 1.9439 | 26.0 | 5.768977 | 1.141914 | 891.0 | 2.940594 | 36.02 | -119.08 |
| 3 | 2.5000 | 22.0 | 4.916000 | 1.012000 | 733.0 | 2.932000 | 38.57 | -121.31 |
| 4 | 3.8250 | 34.0 | 5.036765 | 1.098039 | 1134.0 | 2.779412 | 33.91 | -118.35 |
reg = Ridge(alpha = 1).fit(Xtrain, Ytrain)reg.score(Xtest, Ytest)
0.6043610352312276
使用岭回归算法依然无法提升模型效果,可见该数据集可能没有共线性问题,或者可能有轻微共线性。
from sklearn.model_selection import cross_val_scorealpharange = np.arange(1, 1001, 100)ridge, lr = [], []for alpha in alpharange:reg = Ridge(alpha = alpha)linear = LinearRegression()regs = cross_val_score(reg, X, y, cv = 5, scoring = 'r2').mean()linears = cross_val_score(linear, X, y, cv = 5, scoring = 'r2').mean()ridge.append(regs)lr.append(linears)plt.plot(alpharange, ridge, color = 'red', label = 'Ridge')plt.plot(alpharange, lr, color = 'orange', label = 'LR')plt.title('Mean')plt.legend()plt.show()
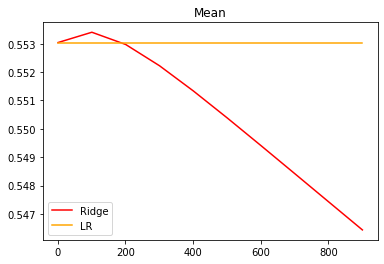
reg = Ridge(alpha = 101).fit(Xtrain, Ytrain)reg.score(Xtest, Ytest)
0.6035230850669467
岭回归在alpha等于101时效果略好于线性回归,但却比alpha等于1时要差。说明该数据集可能没有共线性问题。
细化学习曲线继续观察:
from sklearn.model_selection import cross_val_scorealpharange = np.arange(1, 201, 10)ridge, lr = [], []for alpha in alpharange:reg = Ridge(alpha = alpha)linear = LinearRegression()regs = cross_val_score(reg, X, y, cv = 5, scoring = 'r2').mean()linears = cross_val_score(linear, X, y, cv = 5, scoring = 'r2').mean()ridge.append(regs)lr.append(linears)plt.plot(alpharange, ridge, color = 'red', label = 'Ridge')plt.plot(alpharange, lr, color = 'orange', label = 'LR')plt.title('Mean')plt.legend()plt.show()
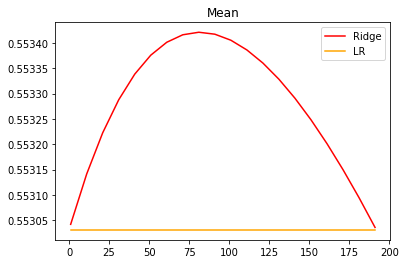
reg = Ridge(alpha = 81).fit(Xtrain, Ytrain)reg.score(Xtest, Ytest)
0.6037194446849763
from sklearn.model_selection import cross_val_scorealpharange = np.arange(1, 1001, 100)ridge, lr = [], []for alpha in alpharange:reg = Ridge(alpha = alpha)linear = LinearRegression()regs = cross_val_score(reg, X, y, cv = 5, scoring = 'r2').var()linears = cross_val_score(linear, X, y, cv = 5, scoring = 'r2').var()ridge.append(regs)lr.append(linears)plt.plot(alpharange, ridge, color = 'red', label = 'Ridge')plt.plot(alpharange, lr, color = 'orange', label = 'LR')plt.title('Variance')plt.legend()plt.show()
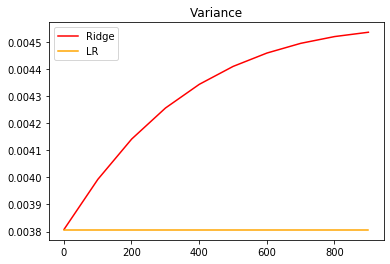
交叉验证结果的均值递减,方差递增,说明随着正则化系数的增大,模型的泛化能力也在逐渐下降。
但在alpha处于1到100之间的时候,模型效果有轻微的提升。但是用测试集检验时却没有发现这样的提升,可能是因为:
- 测试集无法代表全体
- 噪声
from sklearn.datasets import load_bostonX = load_boston().datay = load_boston().targetXtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)#先查看方差的变化alpharange = np.arange(1,1001,100)ridge, lr = [], []for alpha in alpharange:reg = Ridge(alpha=alpha)linear = LinearRegression()varR = cross_val_score(reg,X,y,cv=5,scoring="r2").var()varLR = cross_val_score(linear,X,y,cv=5,scoring="r2").var()ridge.append(varR)lr.append(varLR)plt.plot(alpharange,ridge,color="red",label="Ridge")plt.plot(alpharange,lr,color="orange",label="LR")plt.title("Variance")plt.legend()plt.show()#查看R2的变化alpharange = np.arange(1,1001,100)ridge, lr = [], []for alpha in alpharange:reg = Ridge(alpha=alpha)linear = LinearRegression()regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()ridge.append(regs)lr.append(linears)plt.plot(alpharange,ridge,color="red",label="Ridge")plt.plot(alpharange,lr,color="orange",label="LR")plt.title("Mean")plt.legend()plt.show()
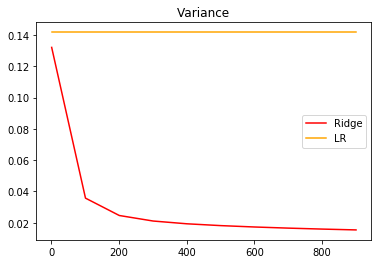
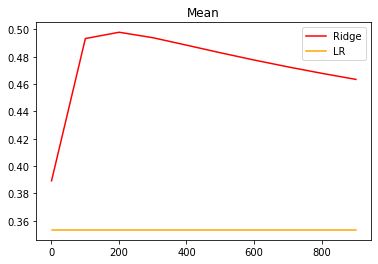
#细化学习曲线alpharange = np.arange(100,300,10)ridge, lr = [], []for alpha in alpharange:reg = Ridge(alpha=alpha)regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()ridge.append(regs)lr.append(linears)plt.plot(alpharange,ridge,color="red",label="Ridge")plt.title("Mean")
Text(0.5, 1.0, 'Mean')
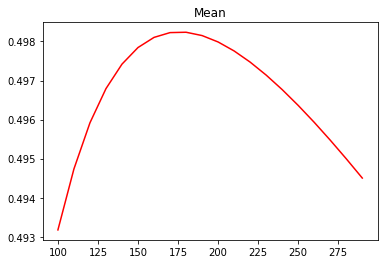
选取最佳的正则化参数取值
岭迹图
既然要选择 的范围,就不可避免地要进行最优参数的选择。通常使用岭迹图来判断正则项参数的最佳取值。传统的岭迹图是一个形似开口的喇叭(根据横坐标的正负,喇叭有可能朝右或朝左):

这一个以正则化参数为横坐标,线性模型求解的系数 为纵坐标的图像,其中每一条彩色的线都是一个系数
。其目标是建立正则化参数与系数
之间的直接关系,以此来观察正则化参数的变化如何影响了系数
的拟合。线条交叉越多,则说明特征之间的多重共线性越高。应该选择系数较为平稳的喇叭口所对应的
取值作为最佳的正则化参数的取值。
岭迹图的缺点:
- 岭迹图的细节难以解释。比如为什么多重共线性存在会使得线与线之间有很多交点?当
很大了之后看 上去所有的系数都很接近于0,难道不是那时候线之间的交点最多吗?
- 岭迹图的评判标准很模糊。哪里才是最佳的喇叭口?在哪里系数开始变得“平稳”?
岭迹图是一个过时的技术。Hoerl和Kennard在1970年提出用来改进多重共线性问题的模型,提出了岭迹图并且向广大学者推荐这种方法,然而遭到了许多人的批评和反抗。大家接受了岭回归,却鲜少接受岭迹图。1974年,Stone M发表论文,表示应当在统计学和机器学习中使用交叉验证。1980年代,机器学习技术迎来第一次全面爆发(1979年ID3决策树,1980年之后CART树,adaboost,带软间隔的支持向量,梯度提升树),从那之后,除了统计学家们,几乎没有人再使用岭迹图了。在现实中,真正被用来选择正则化系数的技术是交叉验证,并且选择的标准非常明确——让交叉验证下的均方误差最小 。
import numpy as npimport matplotlib.pyplot as pltfrom sklearn import linear_model#创造10*10的希尔伯特矩阵X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])y = np.ones(10)#计算横坐标n_alphas = 200alphas = np.logspace(-10, -2, n_alphas)#建模,获取每一个正则化取值下的系数组合coefs = []for a in alphas:ridge = linear_model.Ridge(alpha=a, fit_intercept=False)ridge.fit(X, y)coefs.append(ridge.coef_)#绘图展示结果ax = plt.gca()ax.plot(alphas, coefs)ax.set_xscale('log')ax.set_xlim(ax.get_xlim()[::-1]) #将横坐标逆转plt.xlabel('正则化参数alpha')plt.ylabel('系数w')plt.title('岭回归下的岭迹图')plt.axis('tight')plt.rcParams['font.sans-serif']=['SimHei']plt.rcParams['axes.unicode_minus']=Falseplt.show()
Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.Font 'default' does not have a glyph for '-' [U+2212], substituting with a dummy symbol.

sklearn.linear_model.RidgeCV
使用交叉验证来选择最佳的正则化系数。在sklearn中,可以直接使用带交叉验证的岭回归。
class sklearn.linear_model.RidgeCV(alphas=(0.1, 1.0, 10.0), fit_intercept=True, normalize=False, scoring=None,
cv=None, gcv_mode=None, store_cv_values=False)
这个类与普通的岭回归类Ridge非常相似,不过在输入正则化系数 的时候可以传入元组作为正则化系数的备选,类似于在画学习曲线前设定
for i in 的列表对象。RidgeCV的重要参数,属性和接口:
| 重要参数 | 含义 |
|---|---|
| alphas | 需要测试的正则化参数的取值的元组 |
| scoring | 用来进行交叉验证的模型评估指标,默认是 If None, the negative mean squared error if cv is ‘auto’ or None (i.e. when using generalized cross-validation), and r2 score otherwise. |
| store_cv_values | 是否保存每次交叉验证的结果,默认False |
| cv | 交叉验证的模式,默认None,默认留一交叉验证可以输入Kfold对象和StratifiedKFold对象来进行交叉验证 |
仅仅当为None时,每次交叉验证的结果才可以被保存下来,当cv有值存在(不是None)时,store_cv_values无法被设定为True |
| 重要属性 | 含义 |
|---|---|
| alpha_ | 查看交叉验证选中的alpha |
| cvvalues | 调用所有交叉验证的结果,只有当store_cv_values=True的时候才能够调用,因此返回的结构是(n_samples, n_alphas) |
| 重要接口 | 含义 |
|---|---|
| score | 调用Ridge类不进行交叉验证的情况下返回的 |
import numpy as npimport pandas as pdfrom sklearn.linear_model import RidgeCV, LinearRegressionfrom sklearn.model_selection import train_test_split as TTSfrom sklearn.datasets import fetch_california_housing as fchimport matplotlib.pyplot as plt
housevalue = fch()X = pd.DataFrame(housevalue.data)y = housevalue.targetX.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目","平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
Ridge_ = RidgeCV(alphas = np.arange(1, 1001, 100), store_cv_values = True).fit(X, y)
Ridge_.score(X, y)
0.6060251767338429
Ridge_.cv_values_ # 返回而二维数组
array([[0.1557472 , 0.16301246, 0.16892723, ..., 0.18881663, 0.19182353,0.19466385],[0.15334566, 0.13922075, 0.12849014, ..., 0.09744906, 0.09344092,0.08981868],[0.02429857, 0.03043271, 0.03543001, ..., 0.04971514, 0.05126165,0.05253834],...,[0.56545783, 0.5454654 , 0.52655917, ..., 0.44532597, 0.43130136,0.41790336],[0.27883123, 0.2692305 , 0.25944481, ..., 0.21328675, 0.20497018,0.19698274],[0.14313527, 0.13967826, 0.13511341, ..., 0.1078647 , 0.10251737,0.0973334 ]])
Ridge_.cv_values_.shape# 20640个样本# 10个alpha取值下交叉验证
(20640, 10)
# 平均后可以查看每个正则化系数取值下的交叉验证结果Ridge_.cv_values_.mean(axis = 0)
array([0.52823795, 0.52787439, 0.52807763, 0.52855759, 0.52917958,0.52987689, 0.53061486, 0.53137481, 0.53214638, 0.53292369])
Ridge_.alpha_
101

