回归

预估某板块未来房价 房产估值

分类

房产投资收益预测

数据预处理

.dropna() 布尔过滤异常值

一元回归

  1. import numpy as np
  2. import pandas as pd
  3. import matplotlib.pyplot as plt
  5. %matplotlib inline
  1. data_list = []
  2. for i in range(1, 8):
  3.     try:
  4.         data = pd.read_csv('lianjia{}.csv'.format(i), encoding = 'gbk')
  5.     except:
  6.         data = pd.read_csv('lianjia{}.csv'.format(i))
  7.     data_list.append(data)
  9. data = pd.concat(data_list).dropna()
  1. data.info()
  1. <class 'pandas.core.frame.DataFrame'>
  2. Int64Index: 144531 entries, 0 to 6659
  3. Data columns (total 14 columns):
  4. cjtaoshu          144531 non-null int64
  5. mendian           144531 non-null object
  6. cjzongjia         144531 non-null float64
  7. zhiwei            144531 non-null object
  8. haoping           144531 non-null object
  9. cjdanjia          144531 non-null object
  10. cjxiaoqu          144531 non-null object
  11. xingming          144531 non-null object
  12. cjzhouqi          144531 non-null object
  13. biaoqian          144531 non-null object
  14. cjlouceng         144531 non-null object
  15. cjshijian         144531 non-null object
  16. congyenianxian    144531 non-null object
  17. bankuai           144531 non-null object
  18. dtypes: float64(1), int64(1), object(12)
  19. memory usage: 16.5+ MB
  1. data.head()
cjtaoshu mendian cjzongjia zhiwei haoping cjdanjia cjxiaoqu xingming cjzhouqi biaoqian cjlouceng cjshijian congyenianxian bankuai
0 37 红莲北里店 251.0 店经理 97% 141 43997元/平 红莲北里 3室1厅 57平 郭海龙 36 房东信赖;销售达人;带看活跃 南 北/高楼层/6层 签约时间：2015-05-24 4-5年 马连道
1 37 红莲北里店 159.0 店经理 97% 141 36969元/平 红莲南里 1室1厅 43平 郭海龙 36 房东信赖;销售达人;带看活跃 南/高楼层/7层 签约时间：2015-05-10 4-5年 马连道
2 37 红莲北里店 257.0 店经理 97% 141 39046元/平 常青藤嘉园 1室1厅 65平 郭海龙 36 房东信赖;销售达人;带看活跃 北/低楼层/16层 签约时间：2015-04-26 4-5年 马连道
3 37 红莲北里店 243.0 店经理 97% 141 41313元/平 红莲北里 2室1厅 58平 郭海龙 36 房东信赖;销售达人;带看活跃 南 北/高楼层/6层 签约时间：2015-04-04 4-5年 马连道
4 37 红莲北里店 372.5 店经理 97% 141 42053元/平 广安门外大街 3室1厅 88平 郭海龙 36 房东信赖;销售达人;带看活跃 东 南 西 北/中楼层/18层 签约时间：2015-04-01 4-5年 马连道 
  1. data.cjdanjia = round(data.cjdanjia.str.replace('元/平', '').astype(np.float32)/10000, 2)
  2. # 功能同上 data.cjdanjia = round(data.cjdanjia.str.replace('元/平', '').astype(np.float32).map(lambda x : x/10000), 2)
  1. data.cjshijian = pd.to_datetime(data.cjshijian.str.replace('签约时间：',''))
  2. # 功能同上 data.cjshijian = pd.datetime(data.cjshijian.map(lambda x : x[5:]))
  1. data.info()
  1. <class 'pandas.core.frame.DataFrame'>
  2. Int64Index: 144531 entries, 0 to 6659
  3. Data columns (total 14 columns):
  4. cjtaoshu          144531 non-null int64
  5. mendian           144531 non-null object
  6. cjzongjia         144531 non-null float64
  7. zhiwei            144531 non-null object
  8. haoping           144531 non-null object
  9. cjdanjia          144531 non-null float32
  10. cjxiaoqu          144531 non-null object
  11. xingming          144531 non-null object
  12. cjzhouqi          144531 non-null object
  13. biaoqian          144531 non-null object
  14. cjlouceng         144531 non-null object
  15. cjshijian         144531 non-null datetime64[ns]
  16. congyenianxian    144531 non-null object
  17. bankuai           144531 non-null object
  18. dtypes: datetime64[ns](1), float32(1), float64(1), int64(1), object(10)
  19. memory usage: 16.0+ MB
  1. yuanyangshanshui_data = data[data.cjxiaoqu.str.contains('远洋山水')]
  1. yuanyangshanshui_data = yuanyangshanshui_data.sort_values('cjshijian')
  1. yuanyangshanshui_data = yuanyangshanshui_data.set_index('cjshijian')
  1. yuanyangshanshui_data_2012 = yuanyangshanshui_data['2012':]
  1. plt.figure(figsize = (10, 8))
  2. plt.scatter(yuanyangshanshui_data_2012.index, yuanyangshanshui_data_2012.cjdanjia)
  1. C:\anaconda\lib\site-packages\pandas\plotting\_converter.py:129: FutureWarning: Using an implicitly registered datetime converter for a matplotlib plotting method. The converter was registered by pandas on import. Future versions of pandas will require you to explicitly register matplotlib converters.
  3. To register the converters:
  4.     >>> from pandas.plotting import register_matplotlib_converters
  5.     >>> register_matplotlib_converters()
  6.   warnings.warn(msg, FutureWarning)
  12. <matplotlib.collections.PathCollection at 0x1c89a8289b0>

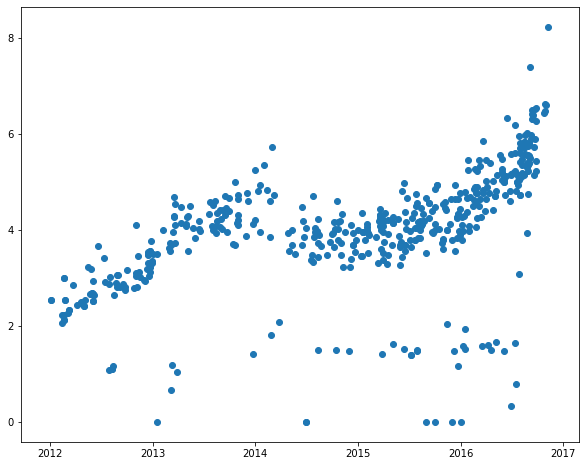
output_12_2.png

  1. yuanyangshanshui_data_2012 = yuanyangshanshui_data_2012[yuanyangshanshui_data_2012.cjdanjia > 1]
  1. plt.figure(figsize = (10, 8))
  2. plt.scatter(yuanyangshanshui_data_2012.index, yuanyangshanshui_data_2012.cjdanjia)
  1. <matplotlib.collections.PathCollection at 0x1c89ab49e48>

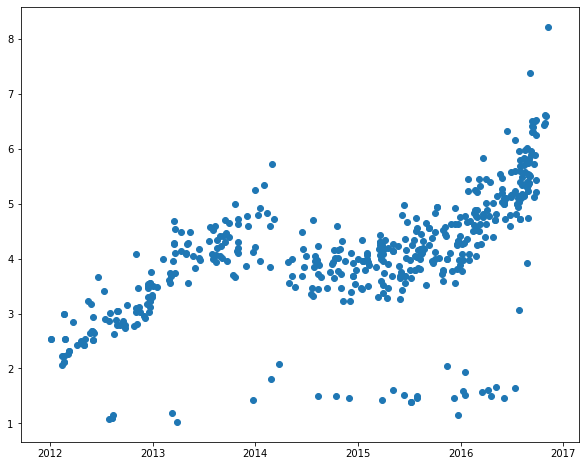
output_14_1.png

  1. yuanyangshanshui_data_2012['time1'] = yuanyangshanshui_data_2012.index - pd.to_datetime('2012-01-01')
  1. yuanyangshanshui_data_2012 = yuanyangshanshui_data_2012.assign(time2 = (yuanyangshanshui_data_2012.index - pd.to_datetime('2012-01-01')).days)
  1. len(yuanyangshanshui_data_2012)
  1. 481
  1. data_time_price = yuanyangshanshui_data_2012[['time2', 'cjdanjia']]
  1. data_time_price.head()
time2 cjdanjia
cjshijian
2012-01-07 6 2.54
2012-01-07 6 2.54
2012-02-13 43 2.22
2012-02-15 45 2.06
2012-02-19 49 2.23 
  1. plt.figure(figsize = (10, 8))
  2. plt.scatter(data_time_price.time2, data_time_price.cjdanjia)
  1. <matplotlib.collections.PathCollection at 0x1c89abd1080>

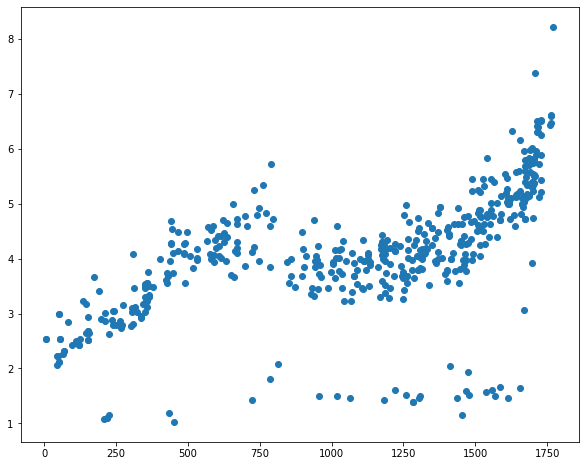
output_20_1.png

  1. from sklearn.linear_model import LinearRegression
  1. model = LinearRegression()
  2. model.fit(pd.DataFrame(data_time_price.time2), data_time_price.cjdanjia)
  1. LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
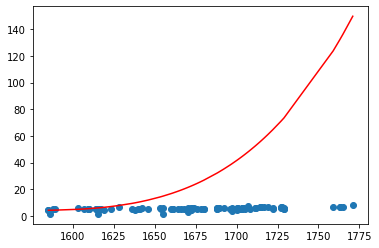
  1. plt.scatter(pd.DataFrame(data_time_price.time2), data_time_price.cjdanjia)
  2. plt.plot(pd.DataFrame(data_time_price.time2), model.predict(pd.DataFrame(data_time_price.time2)), c = 'r')
  1. [<matplotlib.lines.Line2D at 0x1c89eca4c18>]

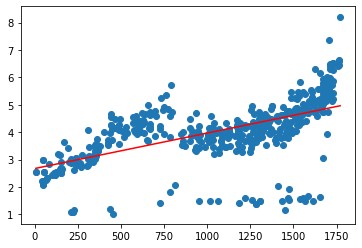
output_23_1.png

多项式回归

  1. model1 = LinearRegression()
  2. X2 = data_time_price.time2 ** 2
  3. X1 = data_time_price.time2
  4. model1.fit(pd.DataFrame({'X2':X2, 'X1':X1}), data_time_price.cjdanjia)
  1. LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
  1. plt.scatter(pd.DataFrame(data_time_price.time2), data_time_price.cjdanjia)
  2. plt.plot(pd.DataFrame(data_time_price.time2), model1.predict(pd.DataFrame({'X2':X2, 'X1':X1})), c = 'r')
  1. [<matplotlib.lines.Line2D at 0x1c8a2dfc588>]

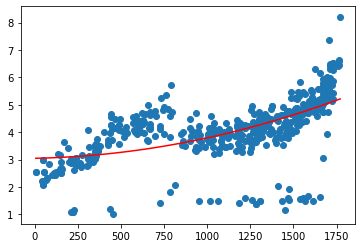
output_25_1.png

  1. model2 = LinearRegression()
  2. X3 = data_time_price.time2 ** 3
  3. X2 = data_time_price.time2 ** 2
  4. X1 = data_time_price.time2
  5. model2.fit(pd.DataFrame({'X3':X3, 'X2':X2, 'X1':X1}), data_time_price.cjdanjia)
  1. LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
  1. plt.scatter(pd.DataFrame(data_time_price.time2), data_time_price.cjdanjia)
  2. plt.plot(pd.DataFrame(data_time_price.time2), model2.predict(pd.DataFrame({'X3':X3, 'X2':X2, 'X1':X1})), c = 'r')
  1. [<matplotlib.lines.Line2D at 0x1c8a148ef60>]

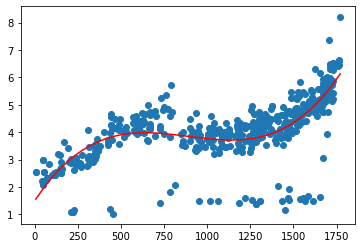
output_27_1.png

  1. from sklearn.preprocessing import PolynomialFeatures
  1. Q3 = PolynomialFeatures(degree = 3)
  2. X3 = Q3.fit_transform(pd.DataFrame(X1))
  3. model3 = LinearRegression()
  4. model3.fit(X3, data_time_price.cjdanjia)
  1. LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
  1. plt.scatter(pd.DataFrame(data_time_price.time2), data_time_price.cjdanjia)
  2. plt.plot(pd.DataFrame(data_time_price.time2), model3.predict(X3), c = 'r')
  1. [<matplotlib.lines.Line2D at 0x1c8a315cd68>]

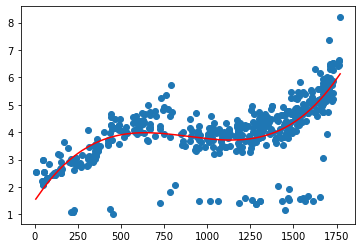
output_30_1.png

模型评价

  1. X = data_time_price.time2
  2. Y = data_time_price.cjdanjia
  4. X_train, X_test = X[:'2016-5'], X['2016-5':]
  5. Y_train, Y_test = Y[:'2016-5'], Y['2016-5':]
  1. Q3 = PolynomialFeatures(degree = 3)
  2. X3 = Q3.fit_transform(pd.DataFrame(X_train))
  3. model_3 = LinearRegression()
  4. model_3.fit(X3, Y_train)
  1. LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
  1. X3_test = Q3.fit_transform(pd.DataFrame(X_test))
  2. plt.scatter(X_test, Y_test)
  3. plt.plot(X_test, model_3.predict(X3_test), c = 'r')
  1. [<matplotlib.lines.Line2D at 0x1c8a31dcc88>]

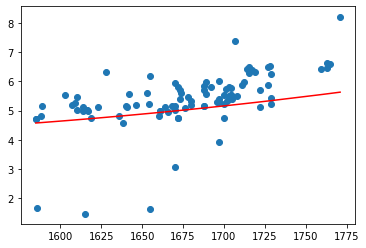
output_34_1.png

  1. sum((model_3.predict(X3_test) - Y_test) ** 2)
  1. 78.51184944045491
  1. Q4 = PolynomialFeatures(degree = 4)
  2. X4 = Q4.fit_transform(pd.DataFrame(X_train))
  3. model_4 = LinearRegression()
  4. model_4.fit(X4, Y_train)
  1. LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
  1. X4_test = Q4.fit_transform(pd.DataFrame(X_test))
  2. plt.scatter(X_test, Y_test)
  3. plt.plot(X_test, model_4.predict(X4_test), c = 'r')
  1. [<matplotlib.lines.Line2D at 0x1c8a30db5f8>]

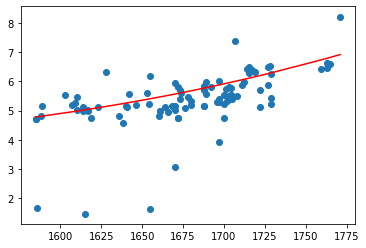
output_37_1.png

  1. sum((model_4.predict(X4_test) - Y_test) ** 2)
  1. 68.29648625212172
  1. Q5 = PolynomialFeatures(degree = 5)
  2. X5 = Q5.fit_transform(pd.DataFrame(X_train))
  3. model_5 = LinearRegression()
  4. model_5.fit(X5, Y_train)
  1. LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
  1. X5_test = Q5.fit_transform(pd.DataFrame(X_test))
  2. plt.scatter(X_test, Y_test)
  3. plt.plot(X_test, model_5.predict(X5_test), c = 'r')
  1. [<matplotlib.lines.Line2D at 0x1c8a3319278>]

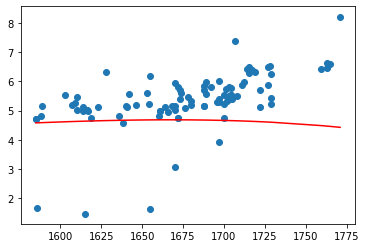
output_40_1.png

  1. sum((model_5.predict(X5_test) - Y_test) ** 2)
  1. 141.17629237528638

从数据出发的模型选择

  1. X_train, X_test = X['2016-1':'2016-5'], X['2016-5':]
  2. Y_train, Y_test = Y['2016-1':'2016-5'], Y['2016-5':]
  1. model = LinearRegression()
  2. model.fit(pd.DataFrame(X_train), Y_train)
  4. plt.scatter(X_test, Y_test)
  5. plt.plot(X_test, model.predict(pd.DataFrame(X_test)), c = 'r')
  1. [<matplotlib.lines.Line2D at 0x1c8a36262b0>]

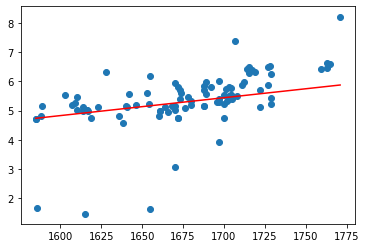
output_44_1.png

  1. sum((model.predict(pd.DataFrame(X_test)) - Y_test) ** 2)
  1. 67.65526778706823
  1. Q3 = PolynomialFeatures(degree = 3)
  2. X3 = Q3.fit_transform(pd.DataFrame(X_train))
  3. model_3 = LinearRegression()
  4. model_3.fit(X3, Y_train)
  6. X3_test = Q3.fit_transform(pd.DataFrame(X_test))
  7. plt.scatter(X_test, Y_test)
  8. plt.plot(X_test, model_3.predict(X3_test), c = 'r')
  1. [<matplotlib.lines.Line2D at 0x1c8a32b2550>]

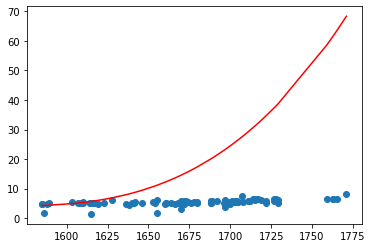
output_48_1.png

  1. sum((model_3.predict(X3_test) - Y_test) ** 2)
  1. 38874.82355826198
  1. Q4 = PolynomialFeatures(degree = 4)
  2. X4 = Q4.fit_transform(pd.DataFrame(X_train))
  3. model_4 = LinearRegression()
  4. model_4.fit(X4, Y_train)
  6. X4_test = Q4.fit_transform(pd.DataFrame(X_test))
  7. plt.scatter(X_test, Y_test)
  8. plt.plot(X_test, model_4.predict(X4_test), c = 'r')
  1. [<matplotlib.lines.Line2D at 0x1c8a33c3748>]

output_50_1.png