向量——表示方式及两种基本运算

The introduction of numbers as coordinates by reference to the particular division scheme of the open one-dimensional continuum is an act of violence. Hermann Weyl

从不同的角度理解向量

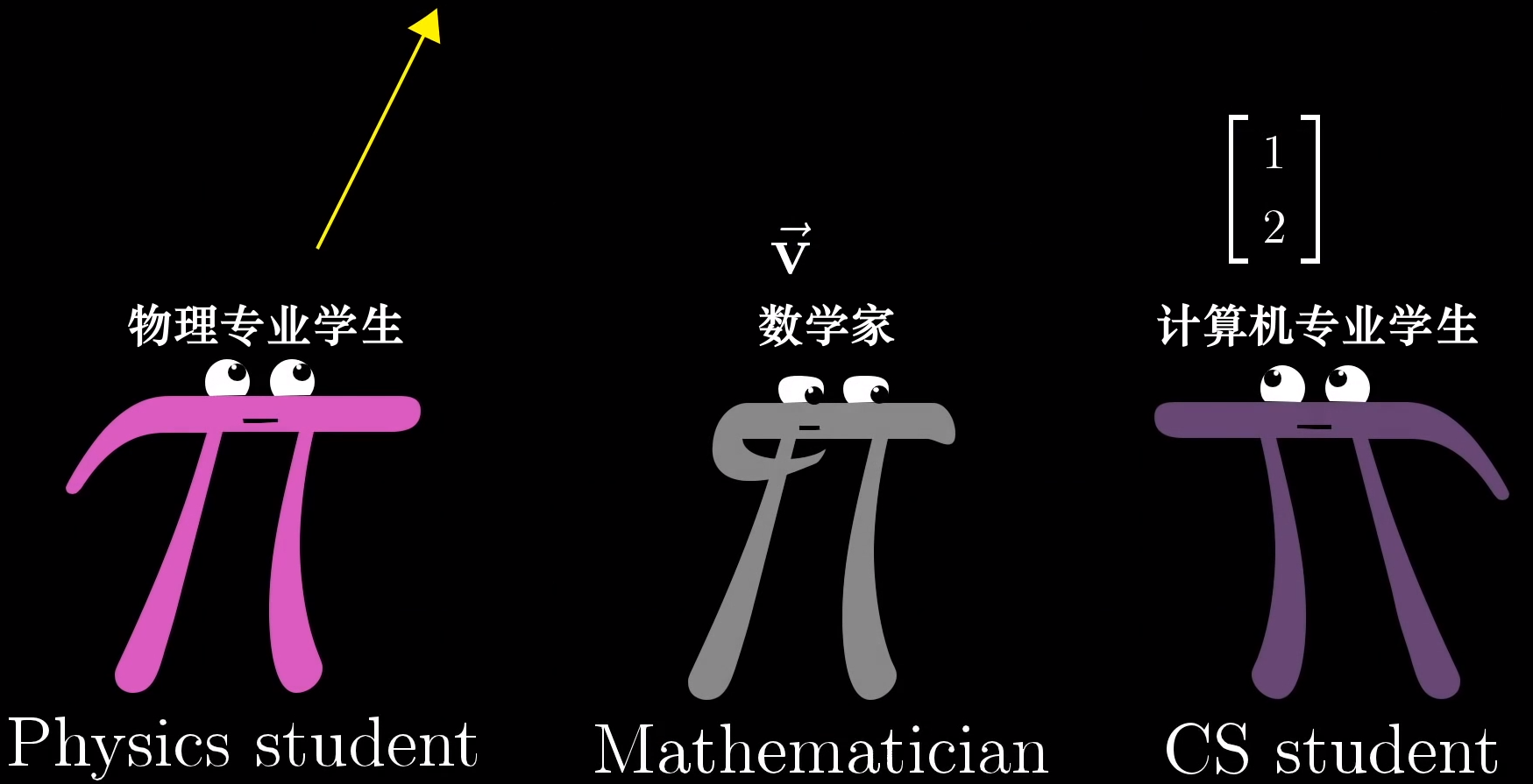
1. 从物理学的角度，向量是 空间中的箭头 ，决定一个向量的是它的长度（Length）和它所指的方向（Direction），只要这两个特征相同，可以自由移动一个变量而使它保持不变。
   平面中的向量是二维的，空间中的向量是三维的。

1. 从计算机科学的角度，向量是有序的数字列表。
   比如分析房价，假设只关注两个特征：房屋面积和总价，用一对数字对每个房子建模。第一个数字代表房屋面积，第二个数字代表总价，，即用二维向量对房屋建模。这里的向量也可以说是列表。要注意。
2. 从数学的角度，两个向量相 加 以及数字与向量相 乘 都是有意义的。

向量形式

二维向量

三维向量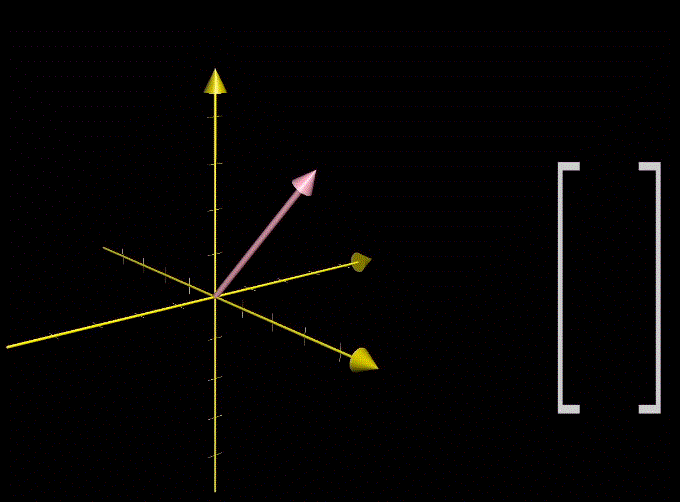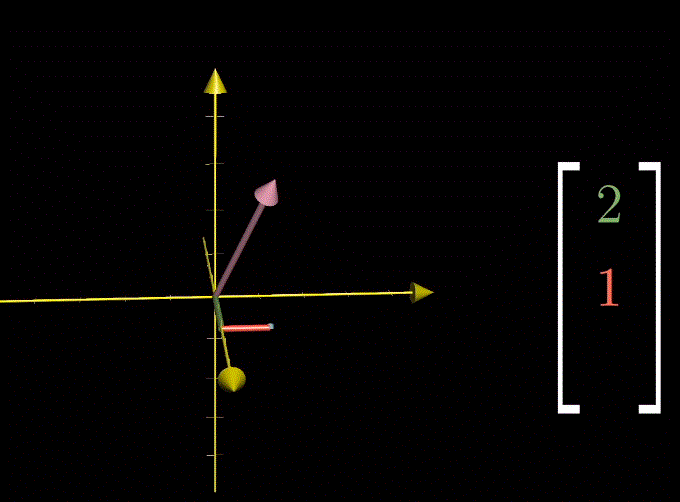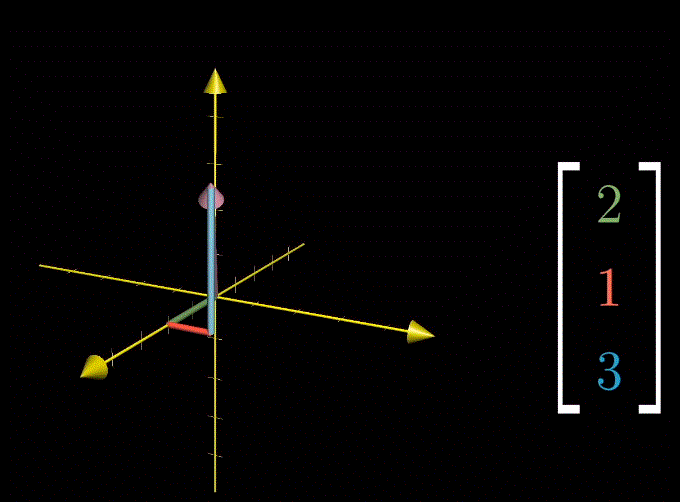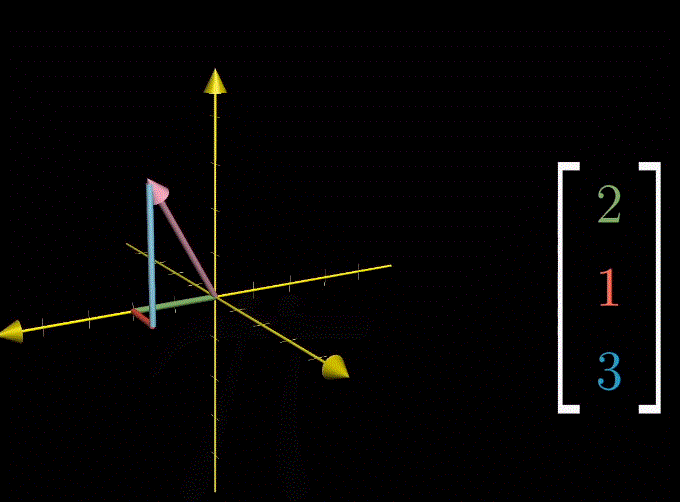

向量运算

向量加法

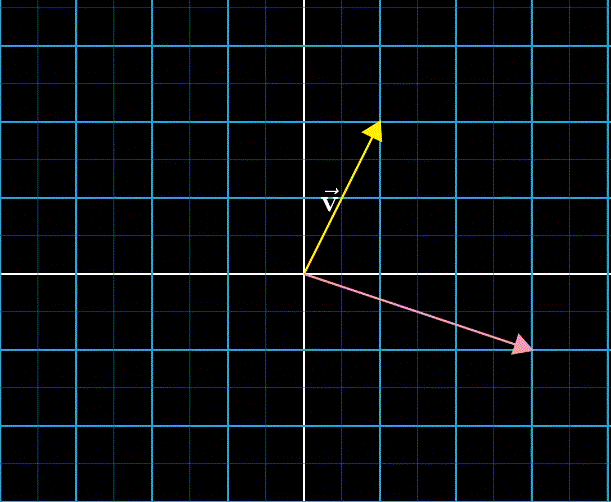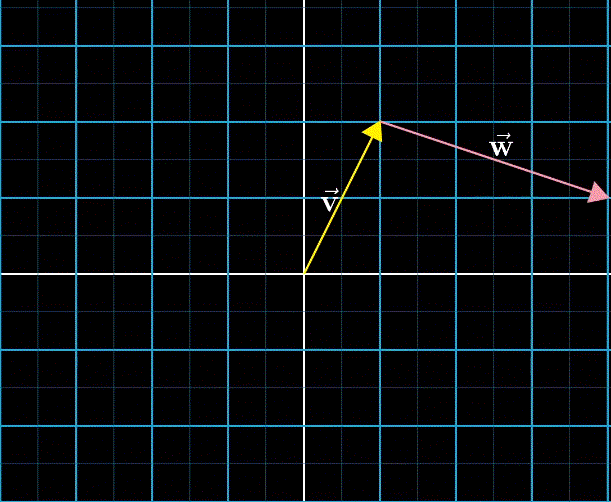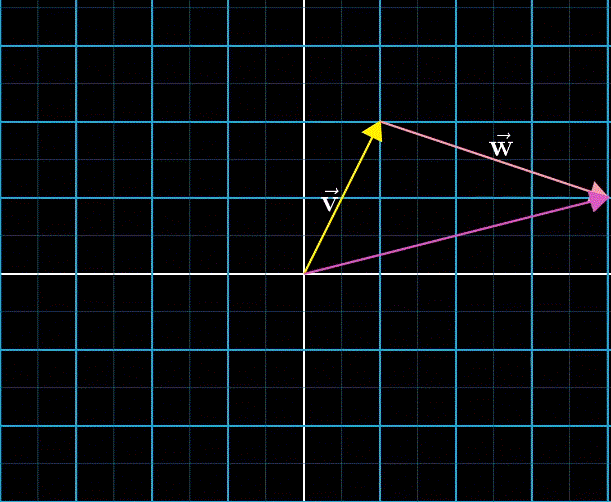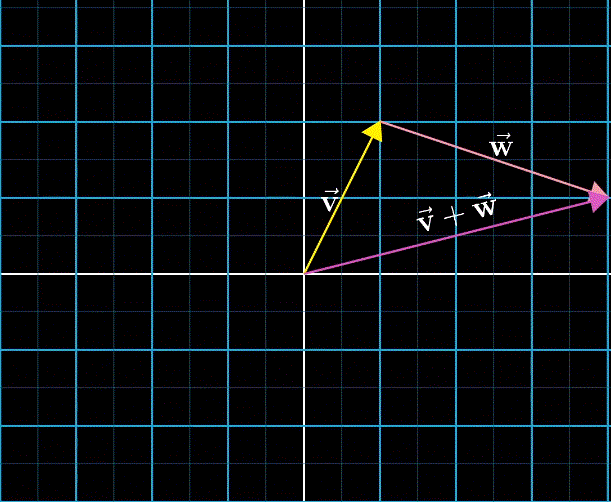
向量加法的定义，是线性代数中唯一允许向量离开原点的情形。将其视作数轴加法的一种扩展。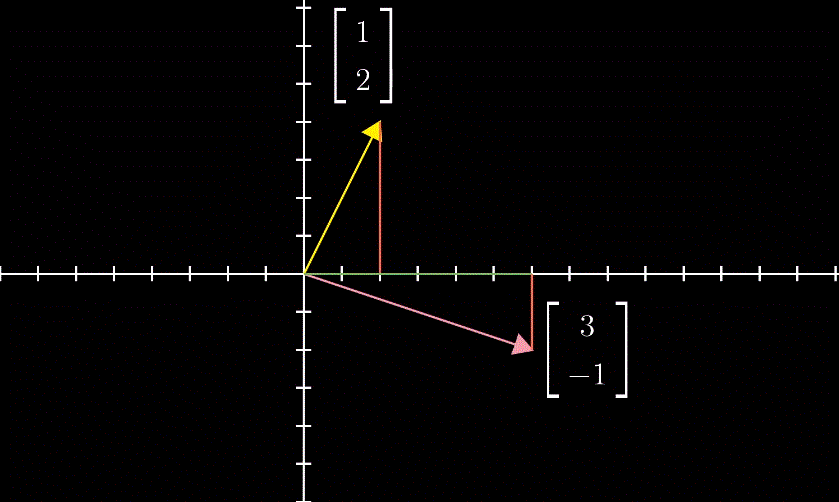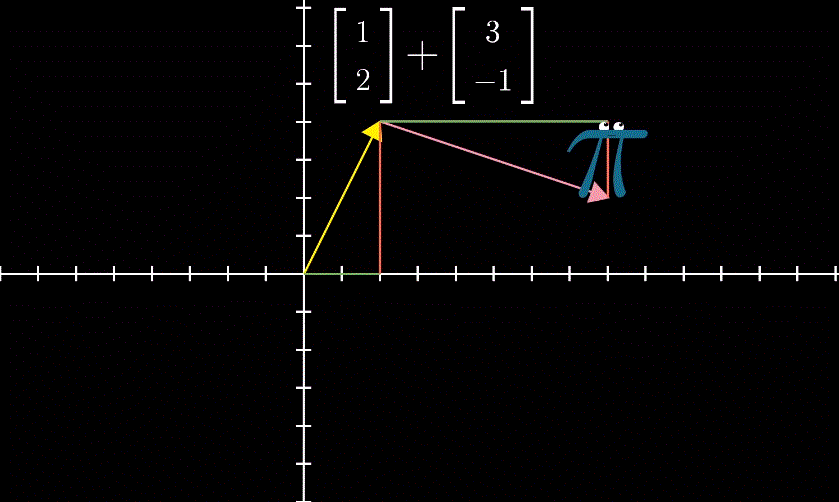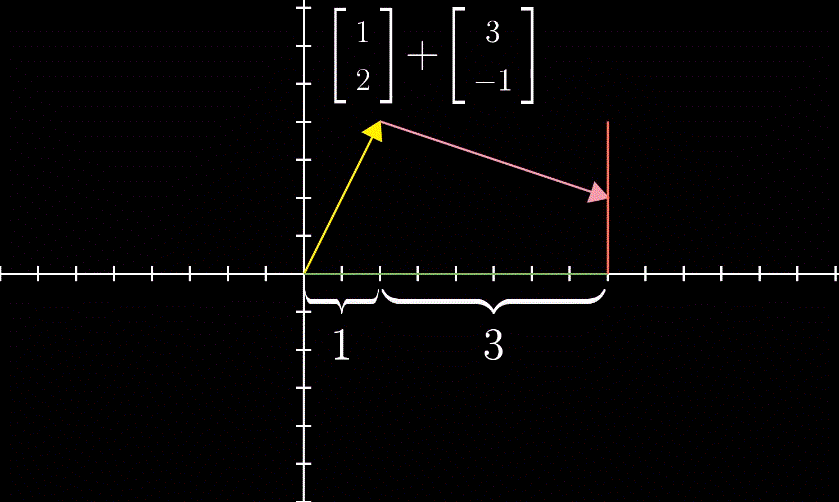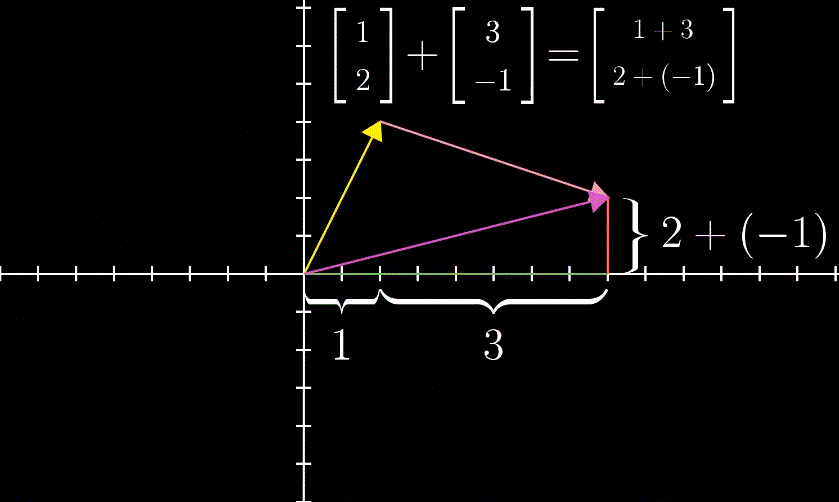

向量数乘

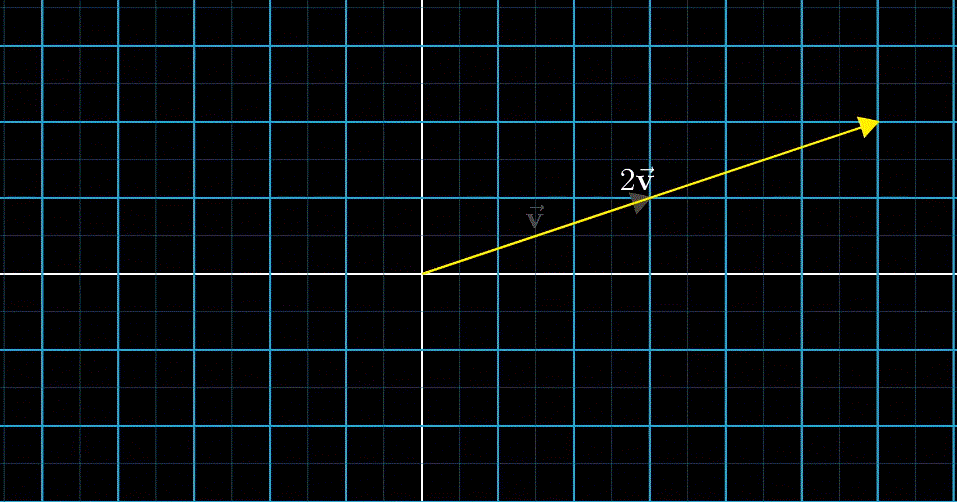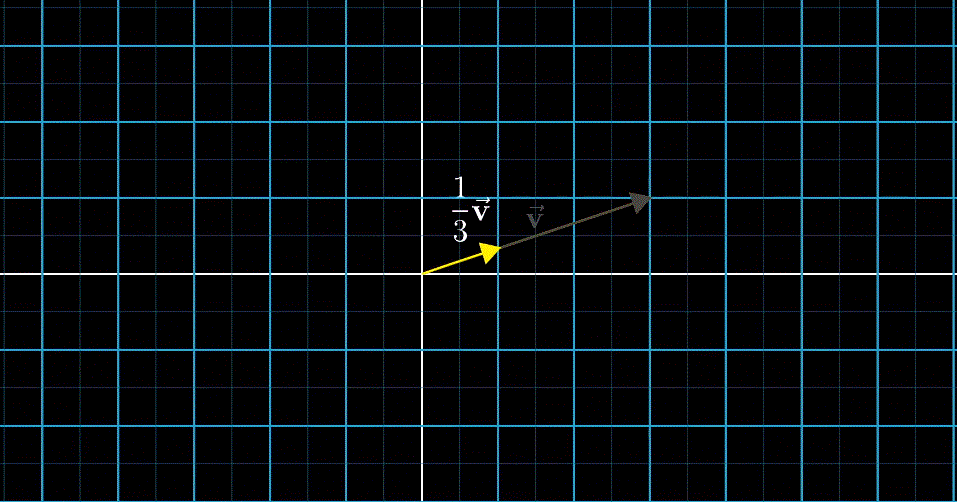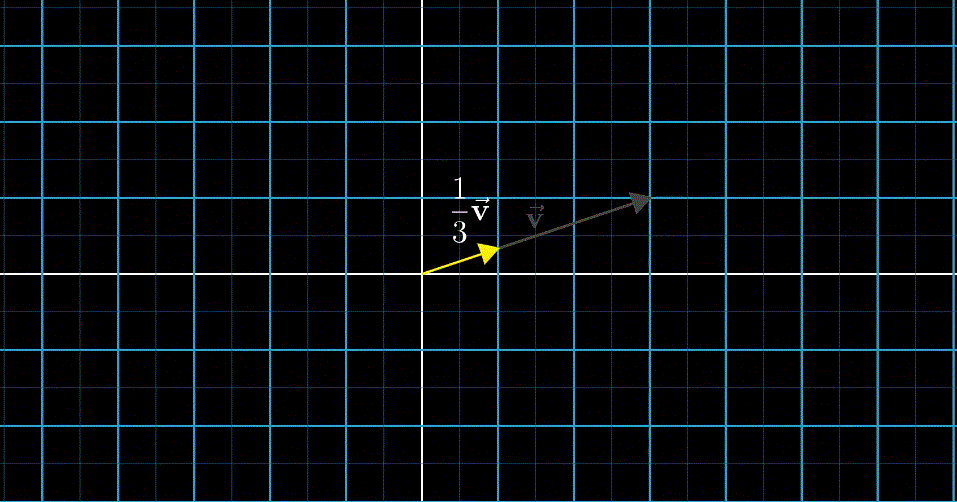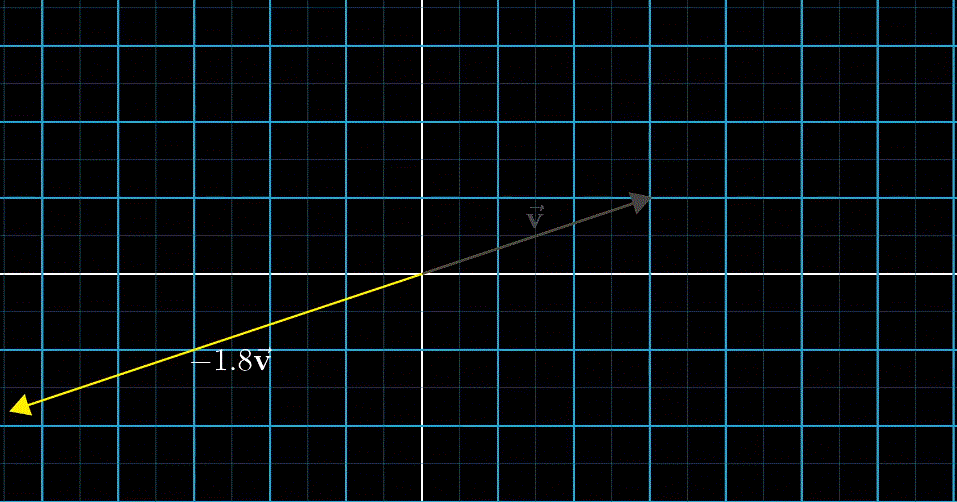
向量数乘在几何角度上看就是缩放（Scaling），用于缩放向量的数被称为标量（Scalars）。实际上，数字在线性代数中起到的作用就是缩放，因此数字和标量两个词可以相互替换。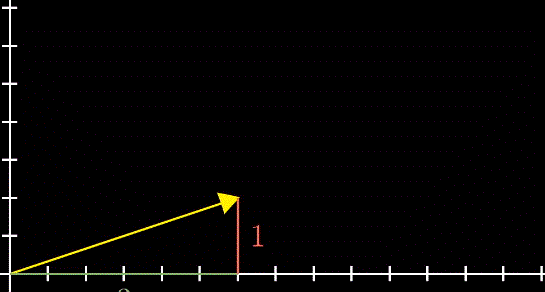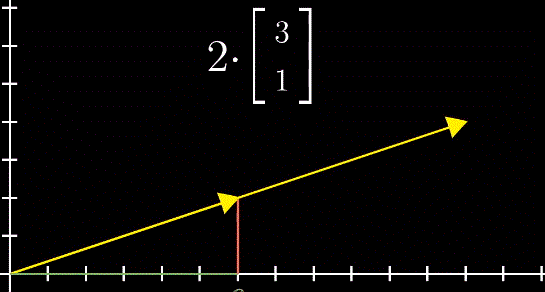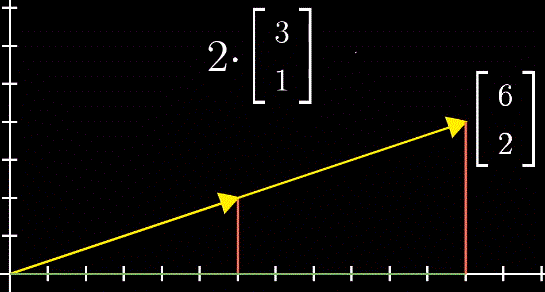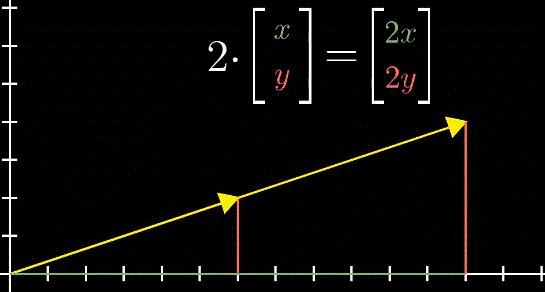

向量的意义

一方面，线性代数为数据分析提供了将大量数据列表概念化、可视化的渠道。让数据样式变得清晰，并让人了解特定运算的意义。
另一方面，线性代数给物理学家和计算机图形程序员提供了一种语言，使他们通过计算机能处理的数字来描述并操纵空间。