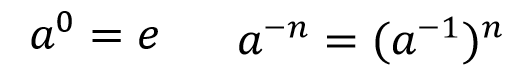第四章：群

4.1 二元运算

二元运算的定义

设A为集合，一个映射**f:A×A→A**称为集合A上的代数运算或二元运算。
一个集合A上的二元运算必须满足以下条件：

• 可运算性：即A中的任何两个元素都可以进行这种运算；
• 单值性：即A中的任何两个元素的运算结果是惟一的；
• 封闭性：即A中的任何两个元素运算的结果都属于A。

  注：一个代数运算一般可用◦、· 、+、×符号来表示。

比如：判断整数集合Z上的加法运算是否是二元运算（代数运算）。

• 可运算性：任意两个数都可以运算，所以满足
• 单值性：运算结果唯一，也满足
• 封闭性：两个整数相加还是整数，所以满足

综上Z上的加法运算是二元运算。

如果是自然数集合S上的减法运算就不是二元运算，因为比如1-2=-1，但是-1不在自然数集合里面，不满足封闭性，所以不是二元运算。

:::info 申明：在之后的运算当中，会把◦称为乘法，把+称为加法，但这只是一种称呼，这里的“乘法”就是传统意义上的两数相乘，同样，“加法”也不代表传统意义上的两数相加。 :::

二元运算的性质

结合律

设◦是A上的代数运算，如果对于A中的任意三个元素 a，b，c都有：
(a∘b)∘c=a∘(b∘c)
则称◦在集合A上满足结合律。

交换律

设◦是A上的代数运算，如果对于A中的任意两个元素a，b，都有：
a∘b=b∘a
则称◦在集合A上满足交换律。

分配律

设◦和+是A上的两个代数运算，如果对于A中的任意三个元素a，b，c都有：
a∘(b+c)=a∘b+a∘c(b+c)∘a=b∘a+c∘a
则称◦对+在集合A上满足分配律。 :::info 以上,如无特别声明,凡是提到代数运算都是指二元运算。 :::

乘法表

代数运算可以用乘法表来表示，例如设A={a1,a2,…,an},·A是上的乘法 ，相应的乘法表如下: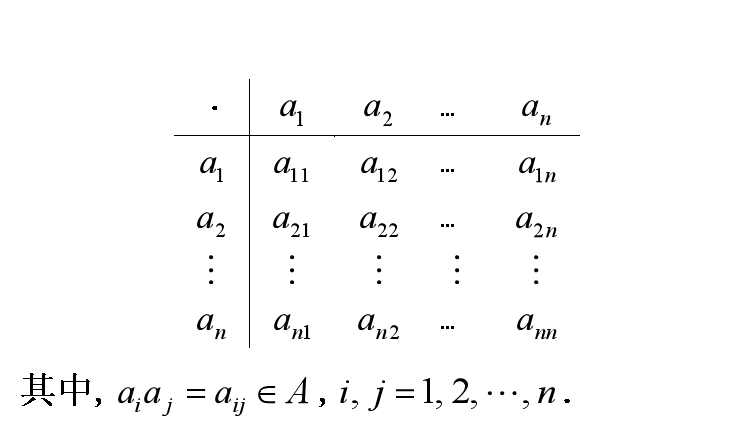

其中第i行``第j列的结果就是：aij = ai · aj

4.2 群的定义和简单性质

群的定义

基本定义

:::info 假设G是一个具有代数运算◦ 的非空集合，如果G是群需要满足一下三个性质：

1. 结合律
2. 具有单位元e，∀a∈G,e∘a=a∘e=a
3. 每一个元素a都有逆元a−1∈G，使得a**−1∘a=a∘a−1**=e

则称G关于代数运算**◦**构成一个群，这个群写作**<G,◦>**。 ::: 举个例子：
全体整数Z对于通常的加法成一个群，这个群称为整数加群，在整数加群中，单位元是0，a的逆元是-a 。

线性群

元素在数域P中的全体n级可逆矩阵对于矩阵的乘法构成一个群，这个群记为GLn(P)，称为n级一般线性群。
这个群当中的单位元为n级单位矩阵，每个矩阵的逆元为它的逆矩阵。GLn(P)中全体行列式为1的矩阵对于矩阵乘法也构成一个群，这个群记为SLn(P)，称为特殊线性群。

这个了解即可。

交换群

如果群G上的乘法运算还满足交换律，即对于群G中的任意元素a,b都有：
ab=ba
则称群G为交换群或阿贝尔群。

比如整数加法群，满足交换律，所以是交换群。

有限群和无限群

若群G中只含有有限个元素，则称群G为有限群；
若群G中含有无限多个元素，则称群G为无限群。
一个有限群G中的元素个数称为群的阶，记为**|G|**。
例如：

对于这个群，|G| = n

群的性质

1. 单位元唯一：群中存在惟一元素e，使得对于所有的a∈G，有

ea=ae=a

1. 逆元唯一：对于群G中的任意一元素a，存在惟一元素b∈G，使得：

ba=ab=e

1. 消去律：设a,b,c是群G中的任意三个元素，则

（1） 若ab=ac，则b=c（左消去律）
（2） 若ba=ca，则b=c（右消去律）

1. 封闭：对于任意两个元素，运算之后的结果仍然属于这个群
2. 对于群G中的任意元素a,b，方程：

ax=b和xa=b
在群G中有唯一解。

1. 对于群G中的任意元素a,b，都有:

**(ab)****-1****=b****−1****a****−1**

群的定理

设G为一非空集合，G上乘法封闭且满足结合律。若对于G中的任意元素a,b ，方程：
ax=b和xa=b
在G中有解，则G是群。
或者利用以下的有限群判定定理： :::info 一个有乘法的有限集合G，若其乘法在G中封闭，且满足结合律和消去律，则G是群。 :::

有单位元和逆元就表示运算具备消去律。

元素的方幂

定义

对于任意正整数n，定义：

再约定：

性质

例题讲解

例题一

:::info 题目：群是一种代数结构，下列说法错误的是
A.群运算必是封闭的 B.群中必有单位元
C.群必满足消去律 D. 群必满足交换律 ::: 解答：
根据定义即可知道，ABC都必须满足，D只有交换群需要满足，普通群无需满足。

例题二

:::info 题目：Zn关于mod n的乘法是否构成群？ ::: 解答：根据定义可知：Zn = {0,1,2,….,n-1}，接下来根据判定定理进行判定即可

1. Zn是一个有限的集合
2. 判断是否封闭：任意两个元素做关于mod n的乘法运算的结果，最终都属于Zn，所以封闭
3. 判断是否满足结合律：显然也满足
4. 判断是否满足消去律：
   1. 判断是否有单位元：很明显这里的1就是单位元
   2. 判断是否有逆元：很明显，这里的0没有逆元，0和任意元素做运算结果都不为单位元1，所以不是所有的元素都存在逆元

综上：Zn关于mod n的乘法不构成群

如果题目改成：Zn中所有**非零元**关于mod n的乘法是否构成群？就构成群

例题三

:::info 题目：整数集合的子集当中关于数的加法是否有构成群的？ ::: 解答：
首先假设存在，所以需要满足群的三个性质：

• 封闭
• 结合律
• 消去律

首先结合律肯定满足，所以不需要再讨论了。
如果需要满足消去律，那么就要保证单位元和逆元，母庸质疑单位元一定是**0**，那么假设存在其他元素a，就一定需要存在元素-a，这样才能满足所有元素都有逆元，最终满足消去律。
最后就是封闭，需要任意两个元素相加最终结果仍然属于这个子集，最简单的例子就是：
{0}或者{-a,0,a}

其中a表示任意整数。

4.3 子群、陪集

子群的定义

基本定义

:::info 如果群G的非空子集合H对于G中的运算也构成一个群，那么H称为G的子群，记为**H ≤ G**。 :::

平凡子群和非平凡子群

:::info 在群G中，仅有单位元素构成的子集合**{e}**和G本身显然都是G的子群。这两个子群称为G的平凡子群，其余的子群称为非平凡子群。 ::: 举个例子：集合整数集合G的加法运算构成一个群，那么：

• H1 = {0}，H2 = G 就是G的平凡子群
• H3 = {-1,0,1} 就是G的非平凡子群

  有限生成群（了解即可）

  设G是群，S是G的子集，G中包含S的最小子群称为由**S**生成的子群，记为<S>。
  如果群**G**自身是由**S**生成的，则称S是G的一组生成元。如果G=<S>，S是有限子集，则称群G是有限生成的。

  子群的判定定理

  定理

  :::info 群G的非空集合H是G子群的充要条件是：对于任意a,b∈H，有：
  ab−1∈H :::

  子群也是群，所以一定也包含单位元，满足封闭性，交换律，消除率。

例题

:::info 题目：设G是群，证明：G中任意多个子群的交集也是G的子群。 ::: 解答：假设Hi是G的子群，一共有n个这样的子群，此时1≤i≤n。
由子群的定义可以知道，这n个子群都必定包含单位元，所以这个n个子群的交集不是空集。
其次由于是交集，所以在这个交集里面任意取两个元素a和b，对于任意的i，都有a，b∈Hi。
根据子群的判定定理可以得到，如果Hi是G的子群，那么其两个元素ab满足：ab−1∈H
于此同时这两个元素又属于这个交集，所以可知：G中任意多个子群的交集也是G的子群。

等价关系和陪集

等价关系

设集合A上的一个二元关系 **~**，满足下列条件： :::info

1. 若 a ∈ A，则 a ~ a ；（自反性）
2. 若a，b ∈ A ， a ~ b ，则 b ~ a ；（对称性）
3. 若 a，b ，c∈ A ， a ~ b ， b ~ c，则 a ~ c ；（传递性） ::: 那么称~是集合A上的一个等价关系。

   陪集

   :::info 定义：设**H**是群G的一个子群。对于G中的任意元素**a**，称集合：
   aH = {ah|h ∈H}
   为H的一个左陪集，简记为 aH。因为H中有单位元素，所以 a ∈aH 。
   同样可以定义右陪集为：
   Ha = {ha|h ∈H} :::

   对于任意元素a ∈ G ， aH与H中有相同的元素个数。因为对于任意h1,h2∈H，由ah1=ah2可推导出 h**1=h2**。

:::info 定理1：设H是G的子群， a ∈ G ，则在等价关系RH下， a的等价类**[a]=aH**。 :::

在群G上定义关系a ~ b当且仅当b**−1**a∈H，是G上的一个等价关系，记为R**H**。

:::info 定理2：设H是群G的一个子群。H的任意两个左陪集或者相等或者无公共元素。群G可以表示成H的若干个不相交的左陪集之并。 :::

元素的阶

指数

群G关于子群H的左陪集的个数称为H在G中的指数，记为**[G:H]**。

拉格朗日定理

设群G是一个有限群，H是群G的一个子群，则H的阶|H|是群G的阶|G| 的因子，而且：
|G|=|H|[G:H]
举个例子：Z4中所有非零元关于mod n的乘法群为G，那么：

• G = {1,2,3}，|G| = 3
• H = {1}，那么|H| = 1
• 所有陪集为：1 H = {1}，2 H = {2}，3 * H = {3}，总共有3个，所以指数[G:H] = 3
• 所以：|G|=|H|[G:H]

  阶的定义

  :::info 生成子群定义：设G是群，对于任意a∈G，定义：
  ⟨a⟩={ai|i∈Z}
  则<a>是G的子群，称为由a生成的子群。 ::: 举个例子：
  假设G = {1,2,3,4}，那么<2> = {2,4,…}

  这里不需要保证ai也属于G。 若G为无限群，则ai一定属于G 若G为有限群，则G为循环群，这个后面会讲到。

:::info 阶的定义：对于群G当中的任一元素a ，若存在正整数k，使得：
ak=e
那么，称满足上式的最小正整数k为元素a的阶，记为**o(a)**。等价地，a生成的子群的阶也为 **o(a)**。若不存在上述的正整数k，则称a是无限阶元，记**o(a) = ∞** ::: 举个例子：

解答：（默认情况下，是求解模运算）
首先写出集合：{1,3}
接下来分别计算1和3的阶：

• 11 mod 4= 1
• 32 mod 4= 1

所以1的阶为1，3的阶是2

推论

:::info 推论一：设G是一个有限群，则G中每一个元素的阶一定是|G|的因子。设|G|=n，对于G中的每一个元素a，有：
an=e ::: 以上面的例子为例，因为G = {1,3}，所以|G| = 2，因子为1,2，正好是1和3的阶。 :::info 推论二：（欧拉定理）设m是正整数，φ(m)为m的欧拉函数，若r∈Zm，gcd(r,m)=1，则：
rφ(m) ≡ 1(mod m) ::: 假设m=4，Zm其中和m互素的数有1和3，以3为例，φ(4) = 2，可得32 ≡ 1(mod 4)

4.4 正规子群、商群和同态

正规子群

定义

:::info 若H是G的子群，且对于任意元素a∈G，均有aH=Ha，则称H是G的正规子群，记为：H⊲G
那么N是G的正规子群，这个正规子群称为G的中心。 ::: 还是那个例子：
此时的G = {1,3}，那么G的子群H = {1}就是一个正规子群。

很明显，一个群的两个平凡子群，都是这个群的正规子群。 这两个群，一个是只包含单位元的群{e}，和群本身G。 如果除了这两个群没有其他的正规子群， 那个这个群G被称为单群。 单群还有一种情况是|G|为素数的情况，此时G也是单群

定理

:::info 设H是G的子群， a∈G。令a−1Ha={a−1ha|h∈H}，则下列条件等价：

1. H是G的正规子群；
2. ∀a∈G，h∈H，有a**−1**ha∈H
3. ∀a∈G，a−1Ha ⊆ H

4. ∀a∈G，a−1Ha = H ::: 上述定理用于推导一个群H是否是G的正规子群。

   例题

   例题一：
   
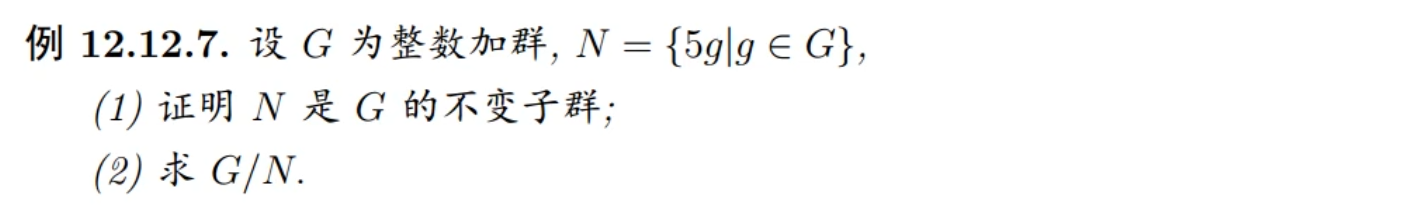
   解答：
   （1）首先证明N是G的不变子群（也就是正规子群），需要有两个步骤：

   • 证明N是G的子群
     • 判断N是否非空
     • 证明N的封闭性
     • 证明N是否有逆元
   • 证明N是G的正规子群

① 首先证明N是G的子群

1. 显然，N≠∅，所以N非空。
2. 其次任取N中的两个元素：5g1和5g2，做加运算可得：5g1 + 5g2 = 5(g1 + g2)∈N，所以满足封闭性。
3. 由于单位元是0，又有-5g1∈N，所以-5g1 + 5g1 = 0 = 5*0∈N，所以存在逆元

② 接下来证明正规子群

1. 在G中任取一个元素a，其逆元为a-1，G显然满足交换律
2. 在N中任意取一个元素5g
3. 根据判定定理，计算a + 5g + a-1，由于有交换律可得，原式=a + a-1 + 5g = 0 + 5g = 5g ∈N，满足等价定理

所以综上，N是G的正规子群。

注意这里的定义的运算是加运算。 商群的计算在后面讲解。

例题二：

原讲解地址：
点击查看【bilibili】

商群

定义

:::info 设H是G的正规子群，记 G/H={aH|a ∈ G}，在集合记 G/H上定义运算：
(aH)·(bH)=(ab)H
则上述定义的运算给出了记 G/H上的一个乘法，且记 G/H在这个乘法下构成群，称为G关于正规子群H的商群。 ::: 这个概念很类似于陪集，区别在于，陪集是元素的集合，而商集是集合的集合。

• 陪集：aH = {ah|h ∈H}
• 商集： G/H={aH|a ∈ G}

陪集当中的h是元素，而商集当中H是集合，商集就是用来表示所有这些陪集的集合。
商群相当于对集合G做了一个等价类的划分，所有陪集加起来实际上就是集合G。

同态与同构

定义

:::info 设G和G'是两个群。f是群G到群G'的一个映射。如果对于任意a ∈ G，映射f满足:
f(ab)=f(a)f(b)
则称f是群G到群G’的一个同态映射。 :::

• 当该映射是满射时，称f是群G到群G'的一个满同态映射。
• 若该映射是一一映射，则称f是群G到群G'的一个同构映射。
• 若群G和群G'之间存在同态（同构）映射，则称群G和群G'同态（同构）。
• 用符号**G≅G'**表示群G和群G'同构。
• G到G自身的同构称为内自同构。

  例题

  题目：G：{2x|x∈Z}关于数的乘法是否构成群？加法群Z与乘法G是否同态？
  证明：
  ① 首先显然G为非空集
  ② 接下来证明G的封闭性、结合律、是否具有单位元，每个元素是否有逆元，这里省略。可以证明得到G构成群。
  ③ 很明显这里需要证明的是G是Z的一个映射
  令f(x) = 2x，任取a,b∈Z可得f(a+b) = 2**a+b ≠ f(a) + f(b) = 2a+ 2b**
  所以可以证明得到G和Z不同构。

  注意这里的f和ab的运算是同一个。比如这里都是加法运算

自然同态

所谓自然同态就是：一个群G与它的每一个商群G/H同态。

同态的象与核

:::info 定义：设f是群G到群G'的一个同态映射，称
f(G)={f(a)|a∈G}
为同态f的象。对于任意a'∈G'，集合：
{a∈G|f(a)=a’}
称为元素a'的完全逆象，记为f−1(a')。
单位元素e'∈G'的完全逆象f−1(e')称为同态f的核，记为 ker(f)。 :::

f(G)是G的一个子群。 自然同态的核为正规子群H。

同态基本定理

:::info 定理：（群同态基本定理）设f是群G到群G'的一个满同态映射，N为f的核，则N是G的一个正规子群，且：
G/N≅G′ :::

4.5 循环群

基本概念

定义

:::info 定义：设G是一个群，若存在一个元素a，使得G=⟨a⟩ ，则称G为循环群。元素a称为G的生成元。

• 若o(a)=∞，G称为无限循环群；
• 若o(a)=n，n是某个正整数，则G称为有限循环群。 ::: 举个例子：整数加法群Z是循环群，其生成元为1或-1。
  由于元素1在运算为加法的时候的幂运算为：1k = k*1。

  这里的幂运算不是传统意义上的乘法幂运算，而是乘法幂运算，也就是k个1相加，这里的k可以是负数。

所以1k可以表示出所有的整数，也就是说G=⟨1⟩，所以整数加法群Z的生成元有**1**。
同理，-1也是整数加法群Z的生成元。

生成元有关定理

:::info 定理1：设G=是无限循环群，则G只有两个生成元为a和a−1。
定理2： 设G=⟨a⟩是n阶循环群，a**k**是G的生成元的充要条件是 gcd(k,n)=1 。
引理1：设a是群G中的一个有限阶元素，o(a)=n,则对于任意正整数m,am=e当且仅当n|m。
引理2：设a是群G中的一个有限阶元素，o(a)=n,则对于任意正整数k , ak的阶为n/gcd(k,n) :::

原根

定义

:::info 定义：设，若的阶为，则称为的生成元或整数m的原根。 :::

这里的φ(m)表示的是的欧拉函数。

举个例子：中7的原根有5。
m = 7的时候，φ(7) = 6
同样因为 (5*5*5*5*5*5) mod 7 ≡ 1 mod 7

注意： 简约剩余系关于乘法构成群，所以这里的运算是乘法而不是加法。 如果是加法的话，这个群里面就没有单位元0。

定理

:::info 定理1：原根的存在性：有生成元当且仅当m = 2,3,p**k,2pk,其中p为一个奇素数，且k≥1。特别的**，如果m是素数，则有生成元。
定理2：循环群的子群是循环群。循环群的商群也是循环群。
定理3：设G=〈a〉是循环群，有

• 若a的阶是无限，则G与整数加群Z同构
• 若a的阶是某个正整数m，则G与Zm加群同构

定理4：中生成元的个数是φ(φ(m)) ::: 例如：由于7是素数，所以有生成元。中21不满足定理，所以没有生成元。

循环群的子群和商群

求解n阶循环群的所有子群

例如：求解12阶循环群G的所有真子群
解答：由于G是循环群，那么必定有生成元**g**。也就是G = <g>
写出12所有的正因子：1,2,3,4,6,12
那么对应的子群对应gx（x是12的正因子）的生成群就是：

• ={e}，
• ={e，g6}
• ={e，g4，g8}
• ={e，g3，g6 ，g9}
• ={e，g2，g4 ，g6 ，g8 ，g10 }
• = G

  根据阶的定义可以知道，g12 = e 如果想要判定n阶循环群的子群的个数，就只需要知道n的正因子有多少个即可。

4.6 置换群

4.7 群中的一些常用算法