第二章：认识数据

由于第一章绪论没什么好讲的，所以直接讲干货

2.1 数据类型和统计

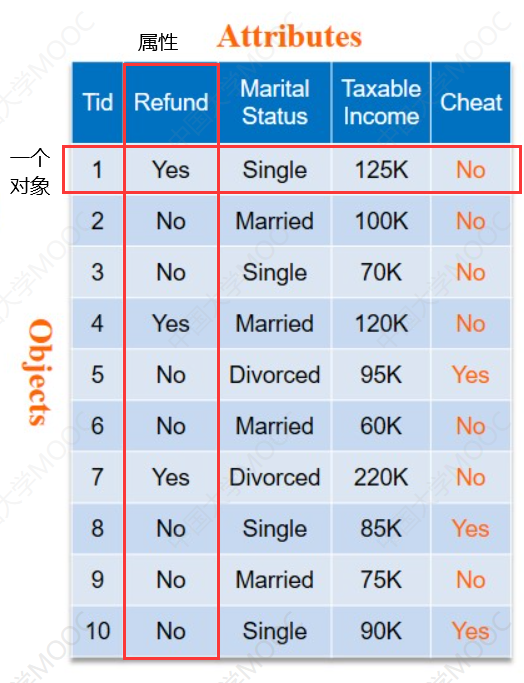
数据对象

• 数据集由数据对象构成
• 一个数据对象代表一个实体
• 例子
  • 销售数据库：客户，商店物品，销售额
  • 医疗数据库：患者，治疗信息
  • 大学数据库：学生，教授，授课信息
• 数据对象所描述的属性
  • 数据库中的行->数据对象
  • 数据库中的列->数据属性

数据对象也可能被称为：

• 样品
• 实例
• 示例
• 数据点
• 元组等

数据的类型

常见的数据类型种类

• 标称类型（也叫类别，状态）
  • hair_color={黑色，白色，黄色，棕色，灰色，克莱因蓝，螺蛳粉}
• 序数
  • 就是一个有意义的顺序（排名）
  • 比如：大小={小，中，大}，等级，军队排名
• 区间标度
  • 有单位长度的度量属性
  • 比如：温度，日历
  • 不存在0点，倍数没有意义
• 比率标度
  • 具有固定零点的数值属性，有序，并且可以计算倍数
  • 比如：长度，重量
• 二进制（特殊的标称类型）
  • 只有0和1两种状态
  • 比如：性别={男，女}，抛硬币={正面，反面}

离散和连续

• 离散属性(Discrete Attribute)
  • 有限或无限可数(countable infinite )个值
  • 例:邮政编码,计数,文档集的词
  • 常表示为整数变量.
  • 注意:二元属性(binary attributes)是离散属性的特例
• 连续属性(Continuous Attribute)
  • 属性值为实数
  • 例:温度,高度,重量.
  • 实践中,实数只能用有限位数字的数度量和表示
  • 连续属性一般用浮点变量表示.

    简单的来说，离散的数据是有限个点，连续的数据是无限个点。

数据统计汇总

数据统计的目的

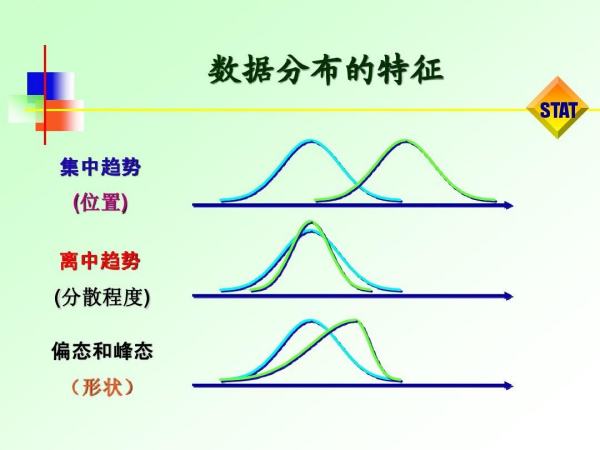
为了更好的了解数据的集中趋势和分布趋势。

• 集中趋势（central tendency）在统计学中是指一组数据向某一中心值靠拢的程度，它反映了一组数据中心点的位置所在。

  简单来说就看数据在图表中在那个值或者区间聚拢。

• 分布趋势就很简单了，就是数据在哪些地方分布。

  数据的统计特征

• 最大值

• 最小值
• 中位数
• 位数
• 离散值
• 方差等

  这里暂时只是介绍，后面遇到了会再进行讲解和归纳。

2.2 数据可视化

箱形图（盒状图）

什么是箱形图

我知道你们来看这个笔记的人大部分都没接触过箱型图，俺也一样，所以这里先补充一下什么是箱型图，如果知道的可以直接跳过至箱形图的作用。

先看一下百度百科的定义：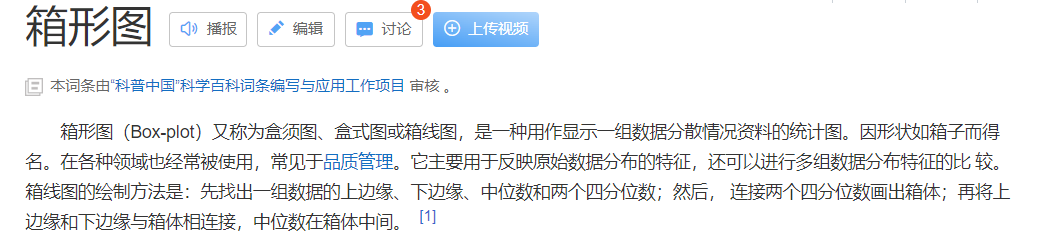

简单来讲就是一种用于反应数据分布情况的图。
箱型图有五个主要的特征：

• 上边缘（最大值）
• 下边缘（最小值）
• 中位数
• 上四分位数
• 下四分位数

这个五个都是在一组数据当中计算得出的值。
如果把数据的大小进行排序，那么这五个值分别代表的了在：

• 上边缘（最大值） 100%
• 下边缘（最小值） 0%
• 中位数 50%
• 上四分位数 75%
• 下四分位数 25%

对应百分比位置的数据。
举个锥简单例子：

一组数据如下：
{1,2,3,4,5,6,7,8,9}

那么：

• 上边缘（最大值）：9
• 下边缘（最小值）：1
• 中位数：5
• 上四分位数：3
• 下四分位数：7

箱形图的绘制就很简单了，一看就懂了：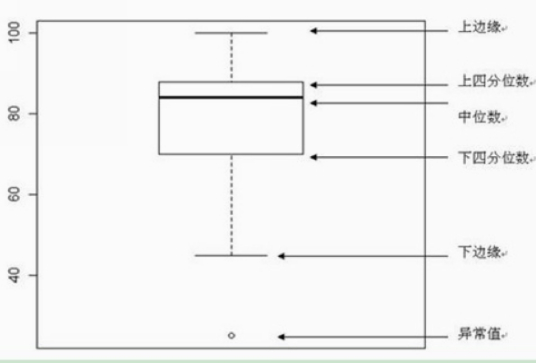

这里会发现有一个空心的原点，这种是异常数据，一般会进行舍去来提高数据的精度。

箱形图的作用

一句话概括就是，箱形图能分析多个数据的离散差异性。
什么是离散差异性呢？
所谓离散程度，即观测变量各个取值之间的差异程度。
举个例子：
我们用箱形图来表示五门课的成绩分布：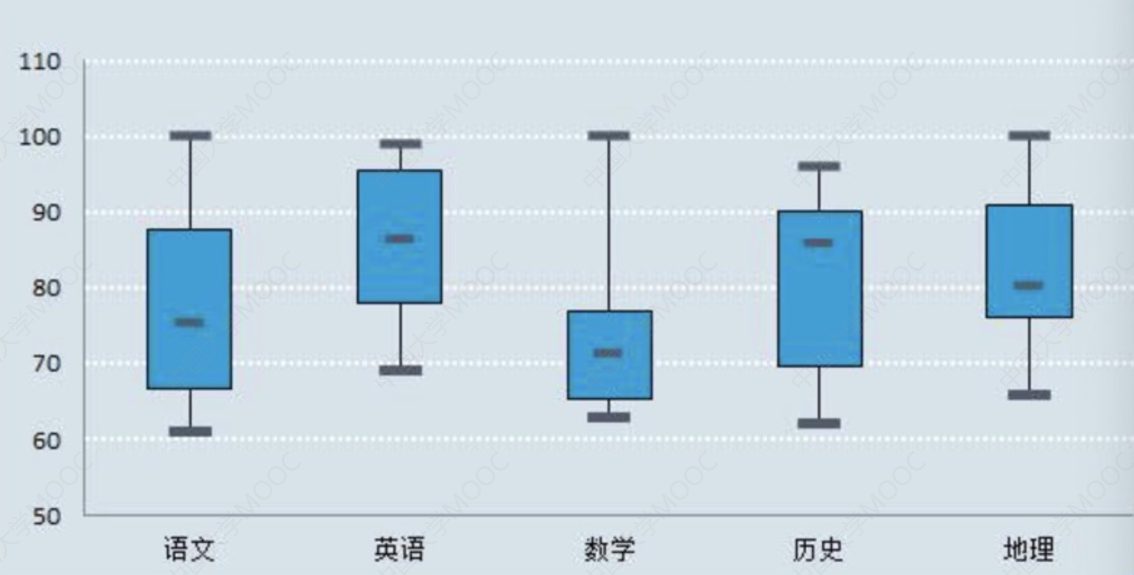

我们主要看中间的箱子部分。
会发现语文和历史差异比较小，箱子所在y轴区间差不太多（这里暂时只要肉眼看看就行，后面会有计算）。
数学和地理差异就比较大。
这就是箱形图的作用。
那如果想要了解单科成绩在各个分数区间的人数分布呢？这个时候箱形图就不再适用了，需要用到直方图。

直方图（柱状图）

这个就不介绍了，柱状图都不知道的建议重修小学数学。
人教版小学数学电子课本
直方图的作用就很简单了：用来分析单个属性的和各个区间的变化。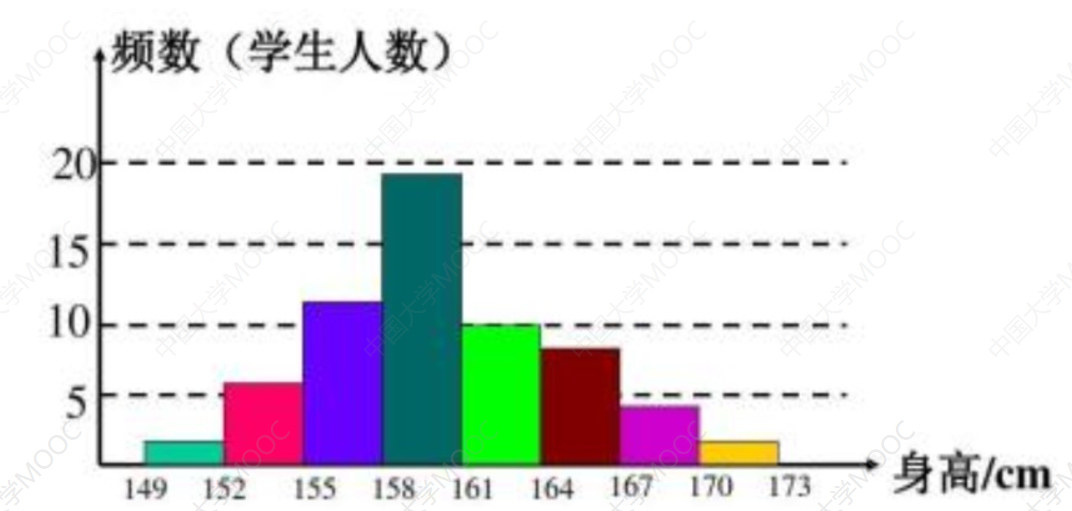

还可以通过设置不同颜色叠加直方图，让不同属性之间的分布比较更明显：

散点图

散点图的主要作用就是用于显示两组数据的相关性分布
数据的相关性有三种：

• 正相关
• 负相关
• 不相关

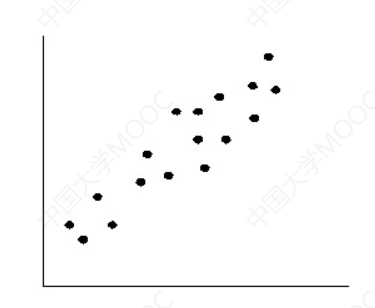
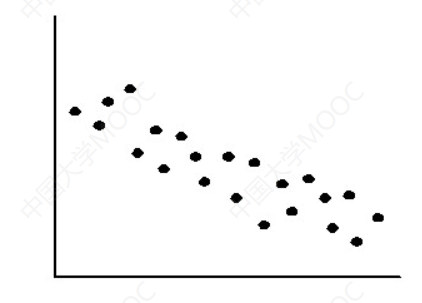
散点图的作用还可以用来做数值预测。
比如：

    房屋销售价格以及房屋的基本信息建立模型,来预测在此期间其他房屋的销售价格。

下面是各个属性对房价的影响：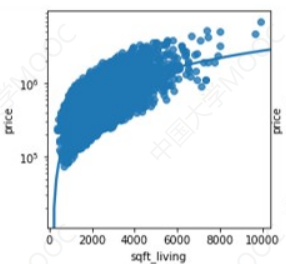


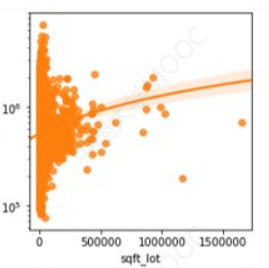
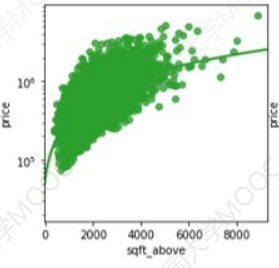
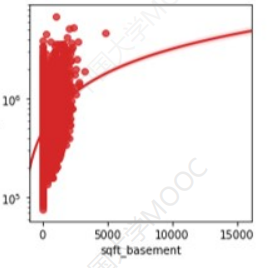
可以注意到，四张图都绘制了一条预测曲线，而相对来讲，房屋面积和建筑面积两个特征比较贴合这个预测曲线，所以如果想要预测房价，房屋的面积和建筑面积更适合作为参考。

2.3 数据相似性

度量数据的相似性和相异性

基本概念

• 相似度Similarity
  • 度量两个数据对象有多相似
  • 值越大就表示数据对象越相似
  • 通常取值范围为[0,1]
• 相异度Dissimilarity (e.g., distance)
  • 度量两个数据对象的差别程度
  • 值越小就表示数据越相似
  • 最小相异度通常为0

• 邻近性Proximity

  • 指相似度或者相异度

    两个矩阵

• 数据矩阵

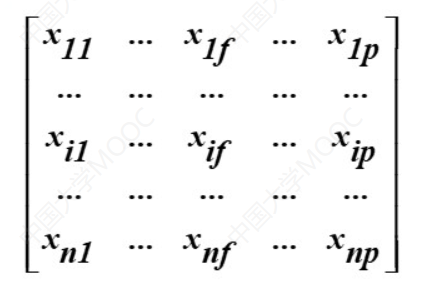
矩阵，每一行代表一个数据，每一列代表一个属性（特征）。
所以这个矩阵所代表的就是n个数据，p个特征的数据矩阵。

这里p个特征也被叫做为p个维度。

• 相异矩阵

这个矩阵是描述数据之间差异的矩阵，这里的d(i,j)表示的是：第i行数据和第j行数据的距离。

这里我们是通过数据之间的距离来描述数据的差异的，就像两个点距离越大，差异就越大，这里只要知道一个大概的概念即可，距离的计算后面会学习。 不难发现这是一个三角矩阵，其中对角线都是0，因为第i行和第i行的差异一定是0。

标称属性的邻近性度量

方法：简单匹配
计算公式：d(i,j) = (p-m)/p
参数解释：

• m：匹配次数
• p：属性总数

来看个例子：
比如我们要计算两个同学兴趣爱好的相异程度：

可以看到这里一共有4个属性（特征、维度），所以这里的p = 4。
接下来就对每个属性一一比较，会发现只有属性1两个同学是相同的，也就是匹配的，剩下三个都不匹配，所以这里m=1。
那么根据公式d(1,2) = (4-1)/4 = 3/4

多个属性同理。

二值属性的邻近性度量

这个比较复杂，就先看实例：
比如下面这是三个人的病历单：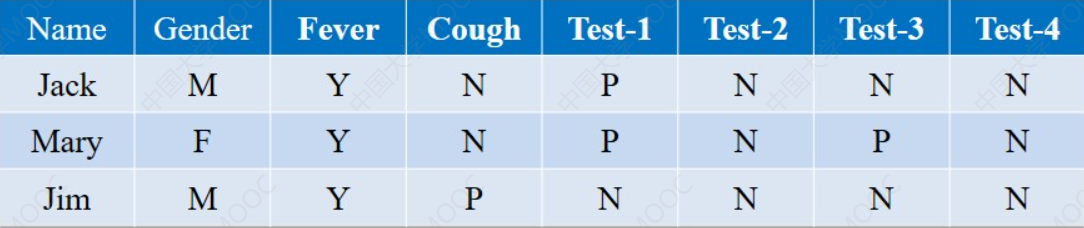

不难发现，这里每个属性的取值只有两个，所以对应我们可以设置令Y = 1，P = 1 ，N = 0。

由于性别（Gender）这个属性比较没有意义所以不设置，Fever里面属性应该是Y或者N，这里由于都生病了所以只有Y。

接下来如果两两对比，我们可以获得一张22的*邻接表：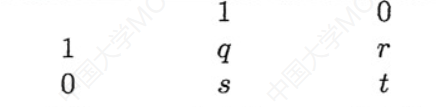

这里来解释一下这个表和四个参数的意思：

• 表的第一行1 0表示的是第一个数据二值属性的取值。
• 表的第一列1 0表示的是第二个数据二值属性的取值。
• q参数代表的是，两个数组所有特征一一对比情况下，二值属性的取值都是1的个数。
• r参数就是第一个数据为0，第二个为1的个数。
• 后面依次类推
• 这里需要比较的特征很明显是从第三列开始到最后一列。

举个例子：我们拿Jack和Mary做比较：

• 都是1的属性有Fever和Test-1，所以q = 2
• 第一个是0，第二个是1的属性的没有，所以r = 1
• 依次类推，s = 0 ，t = 3

所以会发现四个参数之和就是p（属性总数）。

距离公式就很好计算了：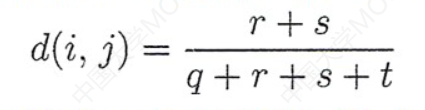

把上面的参数代入即可。

这里分母是所有属性总数很好理解，分子的话就是只要两个数据有差别的进行相加即可。

这里需要补充一点，这种计算法则下，我们通常是默认二值属性两个值的取值是等概率的，然后实际情况下概率不一定都相等，尤其是在这个病例模型下，如果我们想要研究病例的情况，就需要舍去两个数据都是正常的属性（也就是二值属性都取0的时候）。

否则的话就会导致距离计算过小而看不出差异。

那这里的话一般就是会舍去t值。
所以这里我们比较一下Jack和Mary，计算这两个数据的差异性可得：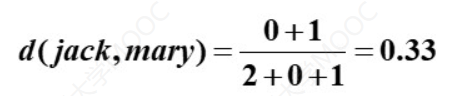

取值概率相等的属性我们称之为：对称二进制属性 不相等的我们称之为：不对称二进制属性

最后补充一个杰卡德系数：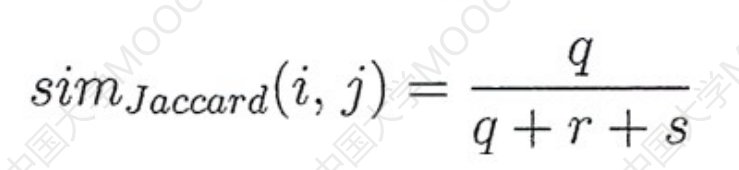

分子就是两个数据的二值属性都是1的个数。

数值属性的邻近性度量

求解数值属性的距离的公式如下：
我们一般称之为：闵可夫斯基距离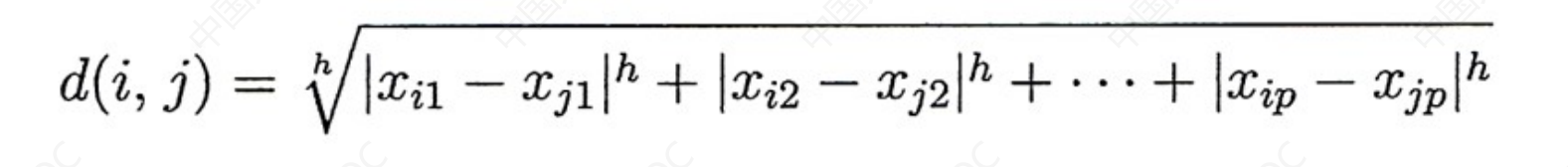

这里的h后面会固定下来，这里当做一个常数即可。

它的性质如下：

h取不同值又表示了不同的距离：

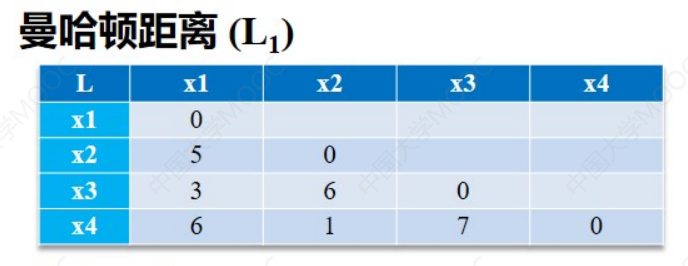
• h=1时，曼哈顿距离：

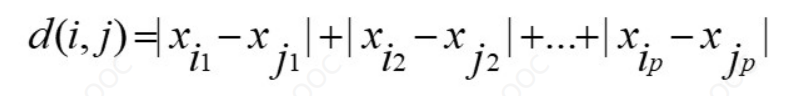
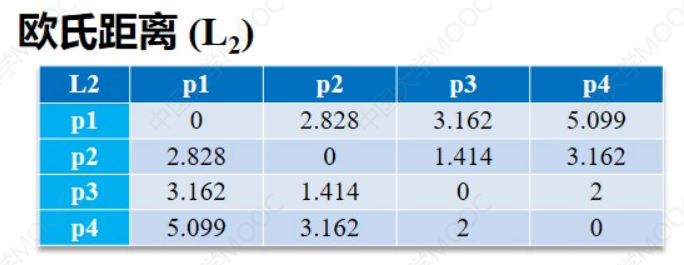
• h=2时，欧式距离：

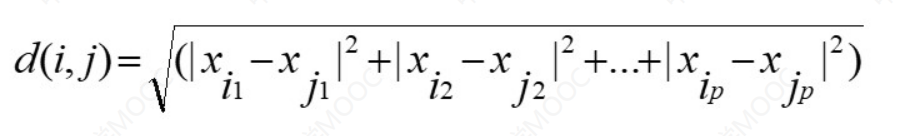
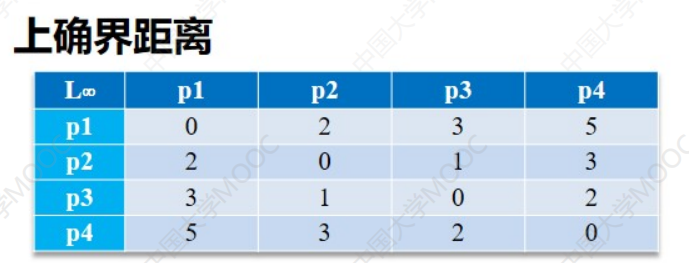
• h-> ∞时，上确界距离：

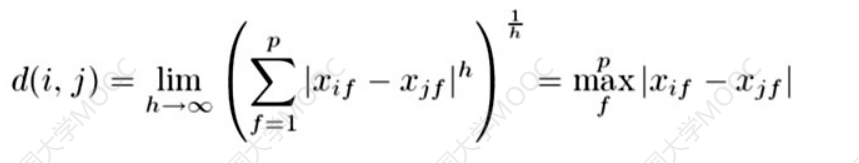
前两个很好理解，第三个上确界距离看着很吓人，其实很简单，就是两个数据中所有属性中差值的绝对值中最大值的。
还不懂举个例子就懂了：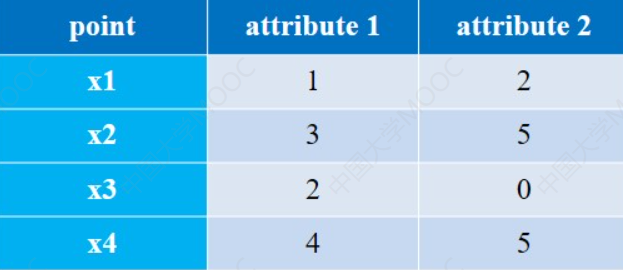

一共两个属性，所以这里 p = 2。
接下来计算d(x1,x2)的三种距离：

• 曼哈顿距离：|3-1| + |5 -2| = 5
• 欧式距离：|(3-1)2|+|(5-2)2| = 13
• 上确界距离：max {|3-1| ， |5-2|} = 3（取两个绝对值中最大的就行了）

是不是真的很简单。
接下来把所有数据的距离算出来就可以得到下面三张表：

附上原链接

数据挖掘_国防科技大学