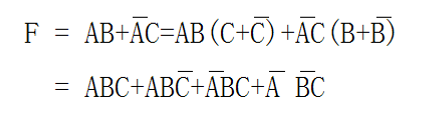判断题
看脸。
化简题
前置知识
根据电路图写出真值
| 电路名称 | 逻辑表示 | 图片 |
|---|---|---|
| 与门 | F = AB | 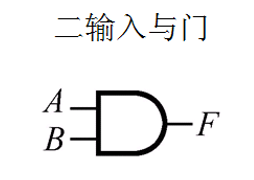 |
| 或门 | F = A + B + C | 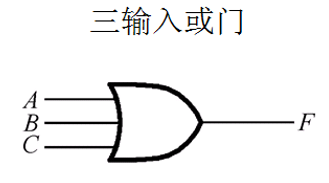 |
| 非门 | F = A̅ | 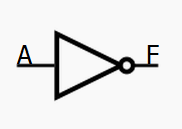 |
| 与非门 |  |
|
| 或非门 | 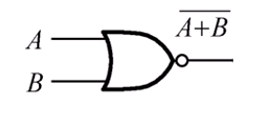 |
|
| 异或门 | 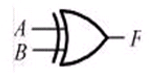 |
|
| 同或门 | 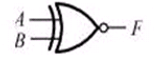 |
循环码
循环码的特点有两个:
- 任何相邻的两个码组中,仅有一位代码不同
- 一组循环码除去最高位之后是对称的
循环码的构成演示如下: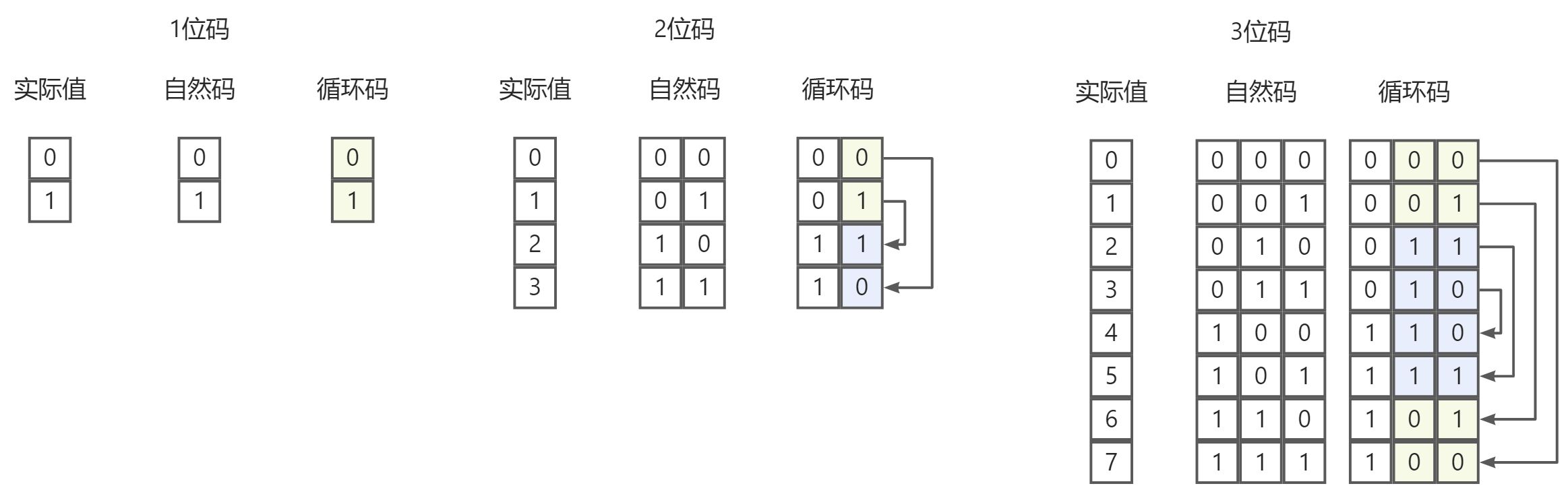
简单来说就是低位进行对称,新增的最高位前半全是0,后半全是1,即可构成循环码。
衍生到四位就是: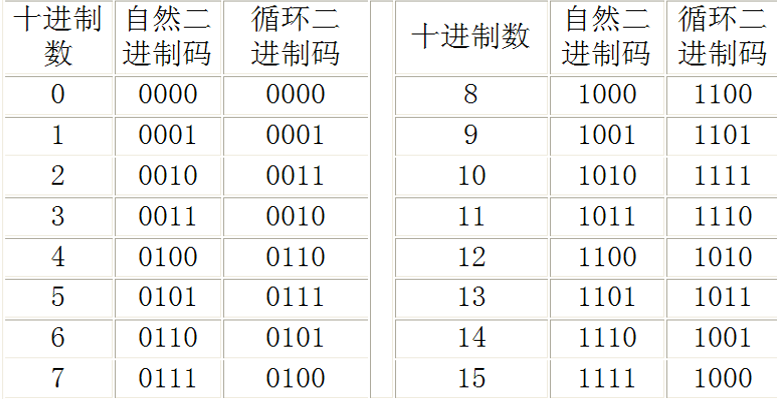
公式化简
布尔代数定律
| 基本定律 | ||||
|---|---|---|---|---|
| 结合律 | ||||
| 交换律 | ||||
| 分配率 | ||||
| 摩根 | ||||
| 吸收律 | ||||
重点记住这里的吸收律。
布尔代数基本规则
- 代入规则
任何一个含有变量A的等式,如果将所有出现A的位置都代入同一个逻辑函数,则恒等式成立。
例如等式:
B(A+C)=BA+BC
现将所有出现A的地方都代入函数A+D,则有
B[(A+D)+C]=B(A+D)+BC=BA+BD+BC
- 反演规则
反演规则是用于求解一个逻辑函数F的非函数的
步骤如下:
① 将F表达式中的与**·**换成或**+**,或**+**换成与**·**
② 将原变量换成非变量,非变量换成原变量
③ 将逻辑1换成0,0换成1。
在替换的时候注意需要先与后或,也就是先把与运算转为或运算
例如:
注意:
和
不等价,前者是AB一起取反,后者是分开取反之后再相乘。
- 对偶规则
某个逻辑恒等式成立的话,其对偶式也成立。
F是一个逻辑表达式,把F中的与·换成或+,或+换成与·;1换成0,0换成1,所得的新的逻辑函数式叫F的对偶式,记为F'。
在替换的时候注意需要先与后或,也就是先把与运算转为或运算
化简技巧
- 并项法
利用 把两个项合并为一项,这样可以消去这个变量A,例如:
- 吸收法
利用,消去多余项B,例如:
- 消去法
利用消去多于项
,例如:
- 💡配项法
卡诺图化简
最小项
A, B, C 三个逻辑变量的最小项有23=8个,分别为:A’B’C’, A’B’C, A’BC’, A’BC, AB’C’, AB’C, ABC’, ABC 其中A’表示A的非,其余类推。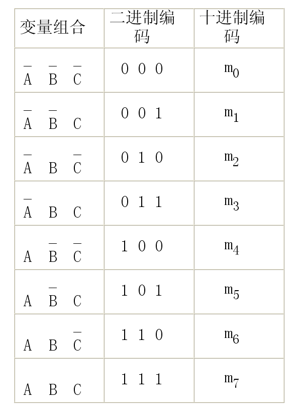
二进制编码的十进制表达就是符号表示的下标。
如何写出最小项
卡诺图的结构


注意:拿这里的
00为例,不是代表A = 0,B = 0,而是在最小项中,最终A与B的结果为0,实际A、B的取值还是1。横纵坐标都是循环码。所以AB从上到下分别是:00 01 11 10,对应的就是二位循环码
卡诺图化简
- 不带有无关项
步骤如下:
- 得到函数的真值表或将函数化为最小项之和的标准形式
- 画出函数的卡诺图
- 合并最小项(即“画圈”)
- 在最小项处标注
1 1格一个也不能漏,否则表达式与函数不等- 包围圈中的
1必须是相邻连续的(矩形边界可以互通,也就是同一行最左边格子和最右边格子视为相邻,同理同一列最上边格子和最下边格子视为相邻) - 包围圈中
1的数量只能是2n个,n一般等于0,1,2,3,4… - 包围圈越大越好
- 包围圈可以互相重叠
- 在最小项处标注
举个例子:
![SSV}]OXB0GQC}W8`51CMEQ.png
首先画出卡诺图:
![Y3]%KQ8NU]1V``E6IAP4ZK.png
画圈:
这里一共四个包围圈:绿色(2个1) + 紫色(2个1) + 红色(4个1) + 黄色(4个1)
黄色是因为四个边角视为相邻。
最后根据包围圈进行合并,每个包围圈中留下**恒为1**和**恒为0**的项。
例如在绿色包围圈中,D一直都是1,A和C一直都是0,所以绿色包围圈留下
在黄色包围圈中,B和D一直都是0,所以黄色包围圈留下
紫色包围圈中,B和D一直都是1,A一直都是0,所以紫色包围圈留下
在红色包围圈中,A和C一直都是1,所以红色包围圈留下
把以上四个包围圈相加可得:
- 带有无关项
与上面唯一的区别是无关项Φ可以被视作1用于连接原本不相邻的1,但是包围圈无需完全包围所有的无关项,仍然只需要包围1即可,此外的过程同上。
见书上P27页 例题19
分析题
电路分析
给出电路,画出波形
电路图如下:
输入波形如下:
其中波形在上表示**1**,波形在下表示**0**,写出各个输出口对应的逻辑表达式即可,根据逻辑表达式和各项输入获取输出口在每一个时间间隔的输出: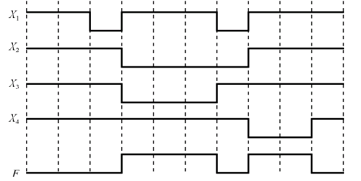
例如这里的,在第一个时间间隔中,A = 1,B = 0,X1应该为1,所以最终波形在上,后面的时间同理。
给出电路,写出电路表达式并化简
列写布尔表达式法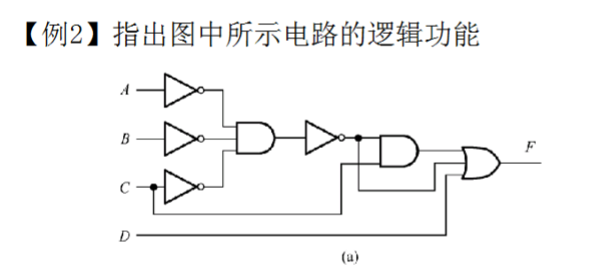
从左往右依次把布尔表达式写出可得:
由前面的基本定律等化简可得:
给出波形,分析电路逻辑关系或表达式
书上P59第8题(节省篇幅就不画图了)。
步骤如下:
① 写出所有F为1的时候,ABCD所在的状态,如果是1就表示为X,如果是0就表示为
比如在第一次F = 1的时候,此时A=0,B=0,C=0,D=1,写作
以此类推可得:
② 对F进行化简(优先找到相同项最多的表达式进行合并)
化简答案不唯一。
时序电路分析
前置知识
如下图所示:
为上升沿触发的时钟信号;
为下降沿触发的时钟信号;
- SR触发器
SR触发器的示意图如下:
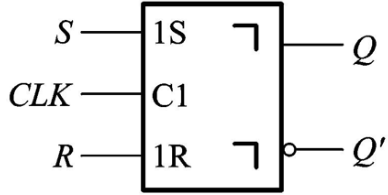
CLK是一个脉冲信号,其逻辑值会随着时间运算改变。
功能表如下:
| 输入 | 输出 | 说明 | |||
|---|---|---|---|---|---|
| S | R | CLK | |||
| 0 | 0 | × | 保持 | ||
| 0 | 1 | ↑ | 0 | 1 | 置0 |
| 1 | 0 | ↑ | 1 | 0 | 置1 |
| 1 | 1 | ↑ | ? | ? | 不稳定 |
状态方程(也叫特征方程)为:
- D触发器
D触发器的逻辑示意图如下: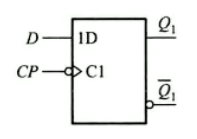
这里CP后面的小圆圈代表:对时钟信号的负脉冲有效,也就是对下降沿敏感 上面的SR没有小圆圈,所以对上升沿敏感 小三角表示是将时钟信号转换成窄脉冲,使触发器按边沿方式工作。
其特性表如下:
| 输入 | 输出 | 说明 | ||
|---|---|---|---|---|
| D | CLK | |||
| 1 | ↑ | 1 | 0 | 置位(存1) |
| 0 | ↑ | 0 | 1 | 复位(存0) |
特征方程为:
- JK触发器
JK触发器逻辑示意图如下:
功能表如下:
| 输入 | 输出 | 说明 | |||
|---|---|---|---|---|---|
| J | K | CLK | |||
| 0 | 0 | ↑ | 保持 | ||
| 0 | 1 | ↑ | 0 | 1 | 置0 |
| 1 | 0 | ↑ | 1 | 0 | 置1 |
| 1 | 1 | ↑ | 交替 |
特征方程为:
JK触发器和D触发器还有强制输入端和
.
- PRE的作用就是让触发器强置为
**1** - CLR的作用就是让触发器强置为
**0**
这两个强制输入信号都是低电平有效,并且不能同时作用,优先级高于JK输入信号。
两个强制输入信号也叫异步输入,一般都处于高电平状态。
- 激励方程和输出方程
激励方程:激励方程也叫作驱动方程,出现在多个触发器(锁存器)组成的时序电路当中,用于表示各个触发器的输入端的输入。
输出方程:也就是整个电路中最终的输出结果。
分析同步时序电路功能
根据时序电路写状态方程和状态图
下图是一个由JK触发器构成的8位计数器: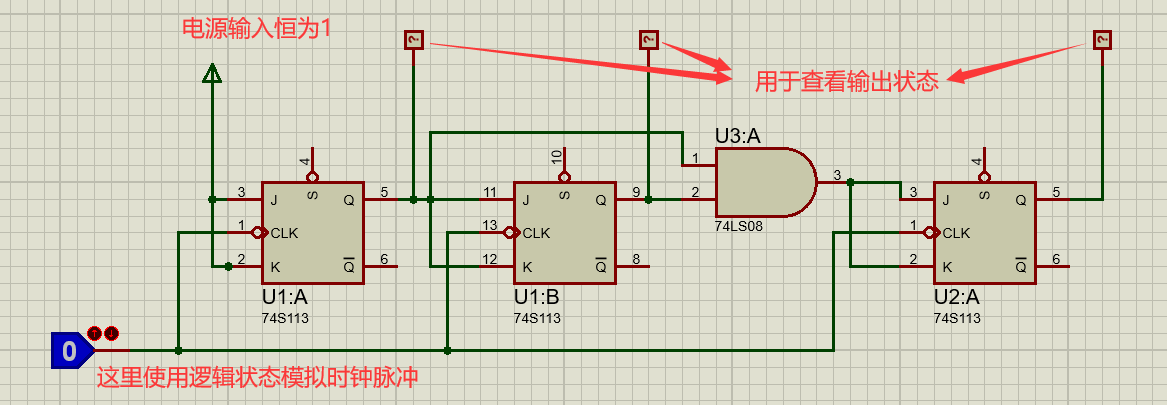
详细可以参照书上P75页。
① 首先根据电路图写出J``K两个输入端的激励方程:
② 由JK触发器的特征方程:
写出电路的状态方程:
③ 写出Q的真值表:
初始状态Q全为0,次态代入上述状态方程即可获得。
| 时钟个数 | PS(现态) | NS(次态) | ||||
|---|---|---|---|---|---|---|
| Q2 | Q1 | Q0 | Q2 | Q1 | Q0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 0 | 1 | 0 | 1 |
| 6 | 1 | 0 | 1 | 1 | 1 | 0 |
| 7 | 1 | 1 | 0 | 1 | 1 | 1 |
| 8 | 1 | 1 | 1 | 0 | 0 | 0 |
| 9(循环) | 0 | 0 | 0 | 0 | 0 | 1 |
时钟个数1时候的次态就是时钟个数2时候的现态。 这里记住:越在电路后面的触发器表示的二进制位数越高。 所以触发器表示的顺序是2,1,0
④ 这里输出方程比较简单,就是直接把三个输出端Q组合成一个二进制数即可,所以最终输出的状态图为:
建议画成圆形,这里实在不太好画所以画的方形。
应用题
设计电路
组合电路设计
例如:设计一个多数表决电路,以判断A、B、C三人中是否多数赞同
首先根据题意写出真值表: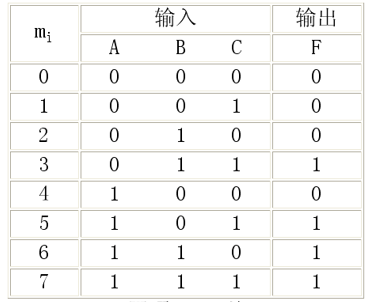
写出F输出为1的表达式: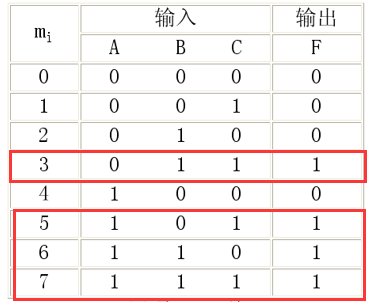
所以F的表达式为:
最后根据表达式画出电路图即可。
画电路图的时候先确定所有的输入,这里就是
A B C,然后从最后倒退门电路,比如这里F最后是由一个四或门组成的。
设计某个功能电路
时序电路的设计
步骤:
- 确定输入输出变量建立原始状态表
- 对原始状态表进行简化
- 状态编码
- 由状态转移表建立最简单的激励函数和输出函数表达式
- 画出逻辑图
时序电路例题
使用与非门和D触发器设计一个同步时序逻辑电路,以检测输入的信号是否为连续的
1 1 0。
① 首先需要确定有多少输入和输出,这里很明显,只有一个输入信号,输出也只有一个,也就是判断信号是否是连续的110,一般记录输入为x,最后的输出为Z。
② 根据题意建立状态表
信号是一位一位输入的,总共需要三位进行判断,一位一位来: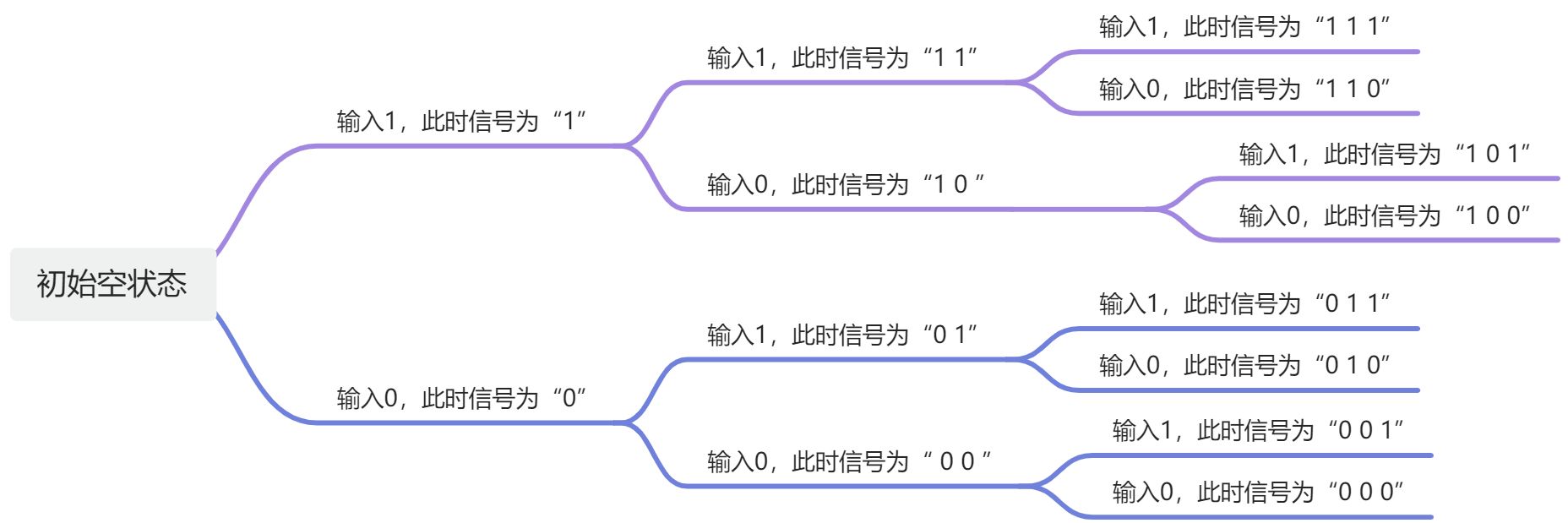
从面可以看出,只有第二种情况Z可以输出1,其余情况都是0。一般来说这就代表了8种状态,但由于本题是连续形式判断,所以并不是三位三位分隔判断,可以出现以下情况: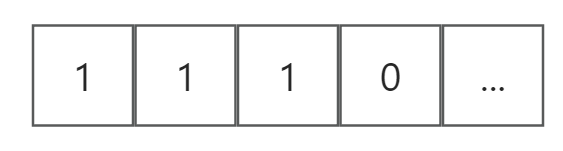
前三位并不符合要求,但是2-4位符合。
③ 画出状态图
所以首先设立一个初始状态S1,代表空值,这种状态下有两种后续情况:x输入的是0,这已经不符合110的判断了,所以直接回滚到S1状态,如果x输入是1,那么进入到下一步进行继续判断,此时设立一个新的状态S2,同理于上,可以画出如下的状态图: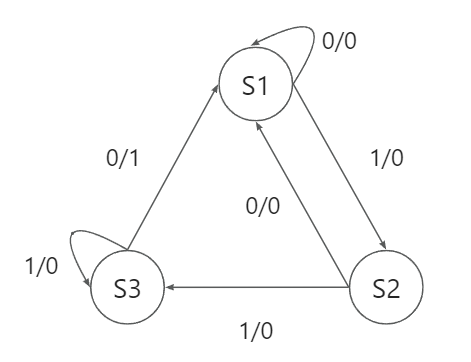
其中
0/1表示的是,此时x输入为0,Z输出为1。
以上会发现总共有三个状态,如果要用二进制编码表示这三种状态,至少需要2位,因为22 =4 >3。
这里就需要两个**D**触发器(题目提供的),输出端口称为y1和y2。三个状态我们从小到大分别用y表示可得: 。
④ 写出状态表
根据上面的状态方程和输入分析,我们知道,如果状态S1(二进制表示就是y1 = 0,y2 = 0)为现态:
- x输入为
**1**的时候,就会进入状态S2(二进制表示就是y2 = 1,y1 = 0),此时次态为**S****2** - x输入为
**0**的时候,就会进入状态S1(二进制表示就是y2 = 0,y1 = 0),此时次态为**S****1**
于是可以以此类推上面三种状态的互相转换,每个状态对应两个输入,也就是有6种情况:
| 输入条件C | 现态PS | 次态NS | 激励 | 输出 |
|---|---|---|---|---|
| x | y**2 y1** | y**2n+1 y1**n+1 | D**2 D1** | Z |
| 0 | 0 0 | 0 0 | 0 0 | 0 |
| 1 | 0 0 | 1 0 | 1 0 | 0 |
| 0 | 1 0 | 0 0 | 0 0 | 0 |
| 1 | 1 0 | 1 1 | 1 1 | 0 |
| 0 | 1 1 | 0 0 | 0 0 | 1 |
| 1 | 1 1 | 1 1 | 1 1 | 0 |
这里的激励是由于D触发器特征方程得来的,D = yn+1
⑤ 写出D的激励函数
这里的做法是画卡诺图:
- 取y**2n+1恒为`1`的情况 | X\y2y**1 | 0 0 | 0 1 | 1 1 | 1 0 | | —- | —- | —- | —- | —- | | 0 | | | | | | 1 | 1 | | 1 | 1 |
对卡诺图化简可得:
这里写成
与的形式是因为题目只提供了与门和非门。
- 取y**1n+1恒为`1`的情况
| X\y2y**1 | 0 0 | 0 1 | 1 1 | 1 0 |
| —- | —- | —- | —- | —- |
| 0 | | | | |
| 1 |
| | 1 | 1 |
对卡诺图化简可得:
⑥ 写出输出函数,也就是当y2 = 1,y1 = 1的时候,也就是处于状态S3的时候,此时x输入为0,Z输出为1,那么也就是:
⑦ 最后根据以上的状态转换方程等,画出逻辑图(P96页 图3.54)(这真教不了,家人们自求多福吧)
注意:由于是同步时序电路,所以一定要加上一个
CLK连接各个触发器
VHDL
VHDL设计
逻辑操作符号 | AND | OR | NOT | NAND | NOR | XOR | XNOR | | —- | —- | —- | —- | —- | —- | —- | | 与操作 | 或操作 | 非操作 | 与非操作 | 或非操作 | 异或 | 同或 |
头文件定义
//定义头文件LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;
实体定义
ENTITY [实体名称] IS // 开始实体定义PORT([输入端口名称];IN bit;[输出端口名称];OUT bit); // 定义实体中的输入输出端口END ENITITY [实体名称]; // 结束实体定义
实体名称不可以是保留字,详情参见书上P152
结构体
ARCHITECTURE [结构体名称] OF [结构体对应的实体] ISBEGIN // 开始定义标志[结构体实际内容]END ARCHITECTURE [结构体名称]; // 结束定义标志
调用组件(元件) ``` ARCHITECTURE [结构体名称] OF [结构体对应的实体] IS
COMPONENT [元件/组件名称] IS
PORT([输入端口名称];IN bit;[输出端口名称];OUT bit); // 定义y元件中的输入输出端口
END COMPONENT; SIGNAL [信号输入端口描述]
BEGIN G1:[元件/组件名称] PORT MAP([组件输入输出功能描述]); // 其中G1作为标识符号,可任意取
END ARCHITECTURE [结构体名称]; // 结束定义标志 ```
例题参见书上P156页 例8
结构体相关
在VHDL程序中, 结构体能包含若干个流程,用于描述系统内部的结构和行为,与顺序无关,可以并行运行 。