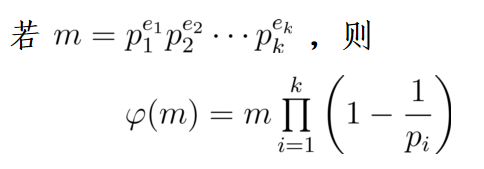第二章： 同余

同余的概念和基本性质

同余的定义

给定3个整数a, b, m，如果m|(a-b)，则称 a模m同余于b 或a，b模m同余，记作**a **≡ **b(mod m)**;
若m ∤ (a-b)，则称a,b模m不同余。

例如： 28 / 5 = 5 … 3 13 / 5 = 2 … 3 28和13除以5的余数相同，就可以说 28模5同余于13，简写为**28 **≡ **13 (mod 5)**

同余的定理

1. a ≡ b(mod m)当且仅当存 在整数k，使得a=km+b
2. 设a ≡ km + r1， b ≡ km + r2,0≤r1<m，0≤r2<m, a ≡ b(mod m)当且仅当r**1=r2**
3. 假设a，b，c，m是正整数
   1. 自反性：a ≡ a (mod m)
   2. 对称性：如果 a ≡ b (mod m)，那么b ≡ a (mod m)
   3. 传递性：如果a ≡ b (mod m)，b ≡ c (mod m)，那么a ≡ c (mod m)
4. 设a， b，d，a1，a2， b1，b2，m为正整数，则
   1. 若a1 ≡ a2 (mod m), b1 ≡ b2 (mod m)，则a1 + b1≡ a2 +b2(mod m)
   2. 若a1 ≡ a2 (mod m), b1 ≡ b2 (mod m)，则a1b1≡ a2b2(mod m)
   3. 若ad ≡ bd (mod m)，且**d和m互素，则a ≡ b(mod m)**
   4. 若a ≡ b(mod m)，d是a，b， m的任意公因数，则
   5. 若a ≡ b(mod m)，d|m，d>0，则a ≡ b(mod d)
   6. 若a ≡ b(mod m)，i =1,2,…,k，则 a ≡ b(mod[m1,m2，…，mk] )

      例题

      例题一

      题目：计算3801（mod 10）
      解答:
      此题的思路就是化简指数，便于计算，在上面的性质当中，能够化简的是性质4里面的b：
      若a1 ≡ a2 (mod m), b1 ≡ b2 (mod m)，则a1b1≡ a2b2(mod m)
      这里的思路就是凑出余数为1的数，比如这里**3****4****(mod 10) = 1**。
      可得**3****4 ****≡ 1 (mod 10) = 1**，根据以上性质，可得**（3****4****）200 ≡ 1200 (mod 10) = 1**

      两边都是乘以自己。

那么原题可得：**（3****4****）200 + 1 ≡ 1200 * 3(mod 10) = 3**

题目二

题目：

解答：
首先可以用a表示出n：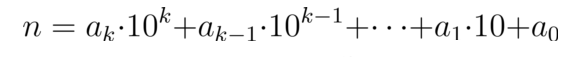

n如果想要整除3，就需要使其余数为0，接下来的思路同上，由于10 ≡ 1 （mod 3），那么就可以得到：
n ≡ a1 + a2 + …. + ak (mod 3)
余数为0，说明a1 + a2 + .... + ak可以整除3，也就证明了(1)。
（2）的证明同理。

同余类与剩余系

同余类的定义

可知对于给定的正整数m，整数同余的关系是一个等价关系。因此全体整数可按照对模m是否同余分为若干个两两不相交的集合，使得每一个集合中的任意两个整数对模m一定同余，而属于不同集合的任意两个整数对模m不同余。
上述的每一个集合称为模m的同余类或模m的剩余类。

简单的来说就是所有除以m余数相同的数的集合，就是一个同余类。

m的剩余类（同余类）有m个，也就是余数的个数（0 到 m-1）。
剩余类的表示如下：
[0] = {…,-2m,-m,0,m,2m,….}
[1] = {…,-2m + 1,-m + 1,1,m + 1, 2m + 1,….}
…
[m-1] = {…,-2m + (m-1),-m + (m-1),m-1,m + (m-1), 2m + (m-1),….}

[]内的就是除以m的余数，{}内的就是同余的集合。

完全剩余系

定义

在模整数m的所有剩余类中各取一个代表元a1,a2…,am , ai∈[i -1],i=1,2…,m，则称a1,a2…,am为模m的完全剩余系。完全剩余系**0,1,2,…,m-1**称为最小非负完全剩余系。
例如：

定理

1. 设m是正整数，整数a满足(a,m)=1,b是任意整数。若**x**遍历模m的一个完全剩余系，则**ax+b**也遍历模m的一个完全剩余系。

   这里的x是指一组数，假设m等于7，那么x = {0,7,14，…}，x中所有的数除以m的余数都一样，就可以说**x**遍历模m的一个完全剩余系。

2. 设m1，m2是两个互素的正整数，如果x遍历模m1的一个完全剩余系，y遍历模m2的一个完全剩余系，那么m1x + m2y遍历模m1m2的一个完全剩余系

   欧拉函数

   定义

   与m互素的剩余类的个数称为欧拉函数,记为φ(m)。
   很显然，φ(m)的值就是一个完全剩余系里面与m互素的数的个数。

   定理

3. 设m,n是两个互素的整数，则φ(mn)= φ(m)φ(n)

4. 对于任意一个素数p，φ(p) = p-1
5. 
   

例题

题目：计算11，121，143和120的欧拉函数。
解答：
首先11是素数，有定理2可得，φ(11) = 11-1 = 10
121 = 11 11 = 112，所以根据定理3可得，φ(121) = 121 (1 - 1/11) = 110
143 = 13 11，可得13和11互素，所以φ(143) = φ(13) φ(11) = 12 10 = 120
120 = 23 3 5，根据定理三可得：φ(120) = 120 (1 - 1/2)(1 - 1/3)(1-1/5)

注意分解的时候，每次保证p值为素数。

简化剩余系

定义

在与m互素的φ(m)个模m的剩余类中各取一个代表元a1,a2…aφ(m)，它们组合成的集合称为模m的一个既约剩余系或简化剩余系。

例如：m = 12 0,1,2,3,4,5,6,7,8,9,10,11就是12的最小非负完全剩余系， 其中1,5,7,11与12互素，{1,5,7,11}那么就是模12的简化剩余系

定理

1. 设m是正整数。整数a满足(a,m)=1。若x遍历模m的一个既约剩余系。则ax也遍历模m的一个既约剩余系。
2. 设m， n,是两个互素的正整数。如果x是遍历模m的一个既约剩余系，y是遍历模n的一个既约剩余系，则**mx+ny**是遍历**模mn**的一个既约剩余系。
3. 假设m是正整数，如果**r∈Z****m**,若（r,m）=1，那么存在整数**s∈Z****m**，使得**rs≡1(mod m)**，整数s就是r模整数m下的乘法逆元。

   r和m互素的时候，才有乘法逆元。 这里的Zm就是m的最小非负完全剩余系。

符号定义

举个例子，假设m = 8，那么关于m的最小非负完全剩余系为：

其中和8互素的数有：

求解乘法逆元

使用辗转相除法即可:

注意前提：必须n和m互素状态下才可以求解乘法逆元。

欧拉定理

这里gcd表示的就是最大公因数，简单来说就是r和m互素。 例如φ（12） = 4，且（5，12） = 1，那么可得54 (mod 12) =1

费马小定理

假设p是一个素数，对于任意的整数a，都有：
ap ≡ a(mod p)
定义：如果a属于m的简化剩余系，那么满足**a****t****≡1(mod m)**的最小正整数t被称为a在模m下的阶，记为：ord(a) = t 。
定理：如果a属于m的简化剩余系，a的阶为t，如果存在正整数s使得**a****s****≡1(mod m)**，那么t|s。

其中t还有一个特点就是t|φ(m)。 φ(m)就是欧拉函数。

例如：m=12，那么m的简化剩余系为：{1,2,5,7,11}
以5为例，容易计算出：ord(5) = 2。

52 = 25，25 ≡ 1 (mod 12)

同时2|φ(12) = 4也成立。