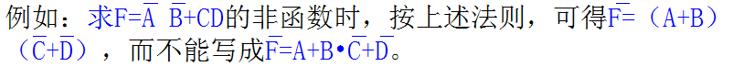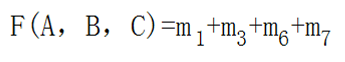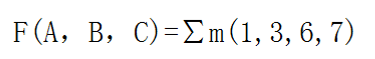1.1 二进制系统

连续量和离散量

连续量：通常被称为模拟量，具有连续性。

例如：温度，压力。

离散量：又称数字量，具有离散性。数字量具有高精度，易存储，易处理等优点。

所以一般情况下都会把连续量转换为离散量进行计算。

开关量

开关量定义

二状态系统（二进制系统）的两个数字状态1和0称为开关量，亦称比特(Bit)。

码的定义

数字状态0和1的组合就被称之为码。
用于表示数字1和0的电平被称为逻辑电平。

数字波形

1.2 数码与数制

进位计数制

现有的常见进制有四种：

  • 十进制
  • 二进制
  • 四进制
  • 十六进制

对应**x**进制的规则是满x进1，例如：

  • 十进制：19 = 1101 + 1 100
  • 二进制：10 = 1 21 + 0 20
  • 四进制：12 = 1 41 + 2 40
  • 十六进制：1A = 1 161 + 10 160

    十六进制十六个数分别表示为：0 1 2 3 4 5 6 7 8 9 A B C D E F A-F表示10-15

进位计数制的相互转换

为什么要转换

因为通常人熟悉的进制是十进制，但实际计算机采用的是二进制，所以需要转换。

其他进制转十进制

如上所示，满x进1。

十进制转其他进制

一个十进制整数转换成八进制数时，按除8取余的方法进行。
一个十进制整数转换成十六进制数时，按除16取余的方法进行。
例如：(725)10 = (?)8

右下角数字即代表进制。

计算步骤如下：

  1. 725 / 8 = 90 …. 5
  2. 90 / 8 = 11 …. 2
  3. 11 / 8 = 1 … 3
  4. 1 / 8 = 0 … 1

把所有的余数倒序加起来就是转换后的进制数（1325）8。

八进制，十六进制转为二进制

由于：
一位八进制数表示的数值恰好相当于三位二进制数能表示的数值。
一位十六进制数表示的数值恰好相当于四位二进制数能表示的数值。
所以直接可以针对每一位直接进行转换。
例如：(67)8 = (?)2
因为：(6)8 = (110)2
又因为：(7)8 = (111)2
直接组合起来就是：(67)**8 = (110 111)2**

十六进制也是类似的，不做演示了，反过来同理。

二进制编码

三个术语

数码:代表一个确切的数字，如二进制数，八进制数等。
代码:特定的二进制数码组，是不同信号的代号，不一定有数的意义。
编码:n位二进制数可以组合成2n个不同的信息，给每个信息规定一个具体码组，这种过程叫编码。

数码由编码可以变成代码。 编码常用的有两种：

  • 二进制编码
  • 二-十进制编码

二进制码

  • 自然码:有权码，每位代码都有固定权值，结构形式与二进制数完全相同。
  • 循环码:无权码，又叫格雷码，每位代码无固定权值，任何相邻的两个码组中，仅有一位代码不同（码距为1)。

    有权码最直白的理解就是每一个有权码都能代表一个确定的值。 例如，以8421码为例（xxxx四位码分别代表8 4 2 1，也就是正常的二进制数）当0110是有权码的时候，它就表示数字6，当0110是无权码的时候，它就没有确切的数字意义。

循环码的特点有两个：

  • 任何相邻的两个码组中，仅有一位代码不同
  • 一组循环码除去最高位之后是对称的

循环码的构成演示如下：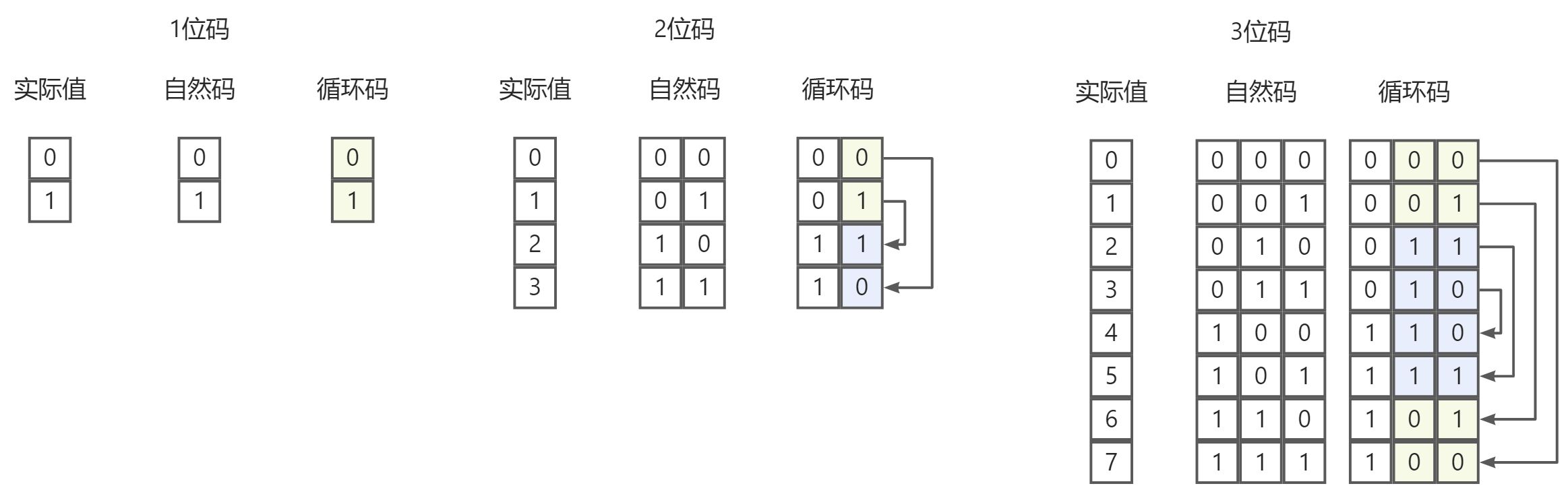
第一章：开关理论基础 - 图1
简单来说就是低位进行对称，新增的最高位前半全是0，后半全是1，即可构成循环码。
衍生到四位就是：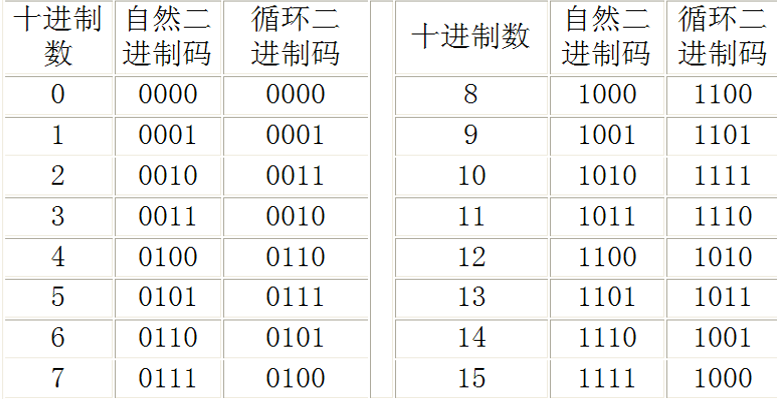
image.png

二-十进制码

BCD码:用二进制代码对十进制数进行编码，它既具有二进制码的形式(四位二进制码)，又有十进制数的特点(每四位二进制码是一位十进制数)。
image.png

8421码和格雷码之前解释过了，余三码就是十进制数加三再转为二进制。

三种码的优缺点：

  • 8421码:编码值与ASCII码字符0到9的的低4位码相同，易于实现人机联系。
  • 余3码:是在8421码的基础上，把每个代码都加0011码而形成的。它的主要优点是执行十进制数相加时，能正确地产生进位信号，而且还给减法运算带来了方便。
  • 格雷码:循环码中的一种，任何两个相邻的代码只有一个二进制位的状态不同，有利于抗干扰。

二进制码和格雷码的转换

  1. 二进制码到格雷码的转换

(1) 格雷码的最高位(最左边)与二进制码的最高位相同。
(2) 从左到右,逐一将二进制码相邻的⒉位相加(舍去进位),作为格雷码的下一位。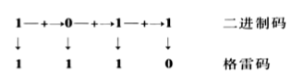
image.png

例如这的格雷码的第二位： 1 = 1 + 0 = 1 第四位： 0 = 1 + 1 = ~~1~~ 0

  1. 格雷码到二进制码的转换

(1) 二进制码的最高位(最左边)与格雷码的最高位相同。
(2) 将产生的每一位二进制码,与下一位相邻的格雷码相加(舍去进位),作为二进制码的下一位。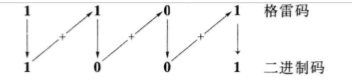
image.png

1.3 逻辑函数及其描述工具

逻辑函数的基本概念

逻辑函数

逻辑函数定义为：F(A1,A2,A3….,An)
其中: A1，A2，…，An为输入逻辑变量，取值是0或1;
F为输出逻辑变量，取值是0或1;
F称为A1，A2，…，An的输出逻辑函数。
逻辑变量和逻辑函数的取值只可能是0或1，没有其他中间值。

逻辑函数的描述工具

image.png

基本逻辑运算

与运算

布尔表达式：F = AB(或者：A·B)
只有当逻辑变量都是1的时候，F才为1，其余情况都是0。
在电路中用与门表示：
image.png
如果是三个变量，真值表如下:
image.png
VHDL描述：
F <= A and B

或运算

布尔表达式：F = A + B
A/B中只要有一个为1，那么F为1
在电路中用或门表示：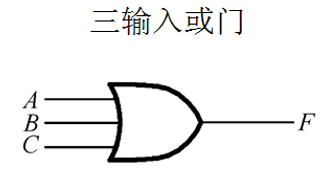
image.png
真值表如下：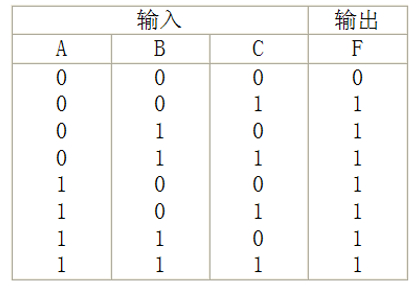
image.png
VHDL描述：
F <= A or B

非运算

布尔表达式：F = A̅
A/B中只要有一个为1，那么F为1
在电路中用非门表示：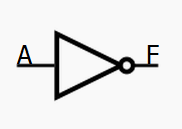
第一章：开关理论基础 - 图11
VHDL描述：
F <= not A

与非运算和或非运算

与非布尔表达式：第一章：开关理论基础 - 图12
先做与运算，在做非运算。
在电路中用与非门表示：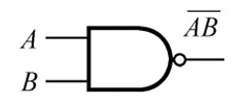
image.png

这里和与门的区别就是多了一个空心的点。

VHDL描述：
F <=not (A and B)

或非布尔表达式：第一章：开关理论基础 - 图14
先做或运算，在做非运算。
在电路中用或非门表示：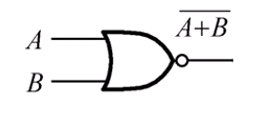
image.png

这里和或门的区别就是多了一个空心的点。

VHDL描述：
F <= not (A or B)

异或运算和同或运算

异或布尔表达式：第一章：开关理论基础 - 图16
在电路中用与非门表示：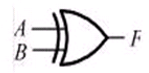
image.png
VHDL描述：
F <= A xor B
同或布尔表达式：第一章：开关理论基础 - 图18
在电路中用或非门表示：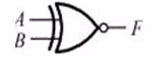
image.png
VHDL描述：
F <= A xnor B

与或非运算

异或布尔表达式：第一章：开关理论基础 - 图20
先与后或在非的一种运算。
VHDL描述：
F <=not ( A and B or C and D)

正逻辑、负逻辑、三态门

这个是用于定义电路输出的逻辑表示

正逻辑

把门电路的输入、输出电压的高电平赋值为逻辑“1”，低电平赋值为逻辑“0”。

负逻辑

把门电路的输入、输出电压的低电平赋值为逻辑“1”，高电平赋值为逻辑“0”。

三态门

三态门是指逻辑门的输出有三种状态：高电平状态、低电平状态、高阻状态。
其中，高阻状态相当于隔离状态（因为高阻状态电阻很大，相当于开路）。
可以理解为一种扩展逻辑功能的输出级，同样也是一种控制开关。

高阻状态可以理解为电路断开。

1.4 布尔代数

布尔代数的基本定理

image.png

重点记住摩根定律和吸收律

利用上述公式可以对逻辑函数进行化简：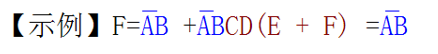
image.png

利用吸收律

布尔代数运算的基本规则

代入规则

任何一个含有变量A的等式，如果将所有出现A的位置都代入同一个逻辑函数，则恒等式成立。
例如等式：
B(A+C)=BA+BC
现将所有出现A的地方都代入函数A+D，则有
B[(A+D)+C]=B(A+D)+BC=BA+BD+BC

反演规则

反演规则是用于求解一个逻辑函数F的非函数第一章：开关理论基础 - 图23的
步骤如下：
① 将F表达式中的与(·)换成或(+)，或(+)换成与(·);
② 将原变量换成非变量，非变量换成原变量;
③ 将逻辑1换成0，0换成1。

在替换的时候注意需要先与后或，也就是先把与运算转为或运算

image.png

对偶规则

某个逻辑恒等式成立的话，其对偶式也成立。
F是一个逻辑表达式，把F中的与·换成或+，或+换成与·;
1换成0，0换成1，所得的新的逻辑函数式叫F的对偶式，记为F'。

在替换的时候注意需要先与后或，也就是先把与运算转为或运算

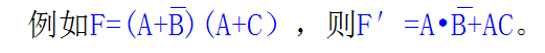
image.png

1.5 卡诺图

卡诺图的结构和特点

最小项

最小项的定义：
n个变量X1、X2、···、Xn的最小项是n个因子的乘积，每个变量都以它的原变量或非变量的形式在乘积中出现，且仅出现一次。
例如：A， B， C 三个逻辑变量的最小项有23=8个，分别为：A’B’C’, A’B’C, A’BC’, A’BC, AB’C’, AB’C, ABC’, ABC 其中A’表示A的非,其余类推。

本定义源自：https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E9%A1%B9/10802305 简单来说就是ABC所有组合。

令A，B，C都取1，那么根据布尔表达式，可以获取一个二进制编码：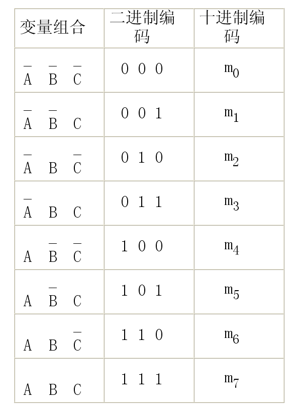
image.png
二进制编码的十进制表达就是符号表示的下标。
例题：写出第一章：开关理论基础 - 图27的最小项表达式：
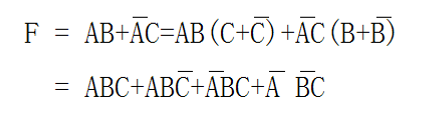
image.png

技巧很简单，就是某一项缺什么就补什么。

接下来就是根据二进制值写出最小项代表符号：
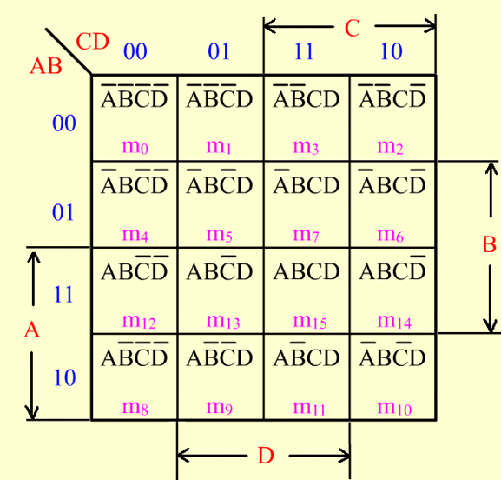
image.png
image.png

卡诺图的结构

卡诺图是逻辑函数的图形表示。利用卡诺图可以简化逻辑函数。
卡诺图一般为二维图形，所以如果是三变量的卡诺图，就需要两个变量为一组：
image.png

注意： 拿这里的00为例，不是代表A = 0，B = 0，而是在最小项中，最终A与B的结果为0，实际A、B的取值还是1。 横纵坐标都是循环码 所以AB从上到下分别是：00 01 11 10，对应的就是二位循环码

那么延伸到四变量：
image.png

利用卡诺图化简逻辑函数

写起来比较麻烦，就直接看视频吧。
点击查看【bilibili】
还有一个带有无关项的处理：
点击查看【bilibili】

1.6 数字集成电路

集成电路的制造技术类型

CMOS系列

CMOS集成门电路已成为主导技术，并有可能取代TTL，CMOS集成门电路功耗小，集成度高。

一般有 +5V和+3.3V两种类型。

TTL系列

TTL:晶体管-晶体管逻辑电路工艺制造技术的英文缩写。
不会对静电放电非常敏感。
TTL速度快，但集成度不如CMOS集成门电路。

通常由5V直流电提供

集成电路的封装类型

插孔装配

image.png

平面装配

image.png

集成电路的规模类型

(1) 小规模集成电路SSI:
单个芯片上集成12个以下的门，实现基本逻辑门的集成。
(2) 中规模集成电路MSI:
单个芯片上集成12～99个门，实现功能部件级集成.

如数据选择器、数据分配器、译码器、编码器、加法器、乘法器、比较器、寄存器、计数器。

(3) 大规模集成电路LSI:
单个芯片上集成100~9999个门电路，实现子系统集成。
(4) 超大规模集成电路VLSI:
单个芯片上集成10000~99999个门电路，实现系统级集成。
(5) 巨大规模集成电路ULSI:
单个芯片上集成10万个以上的门电路，实现大型存储器、大型微处理器等复杂系统的集成。

集成电路的使用特性

负载能力

指的是：一个逻辑门的输出端所能连接的下一级逻辑门输入端的节点个数，称为该逻辑门的扇出。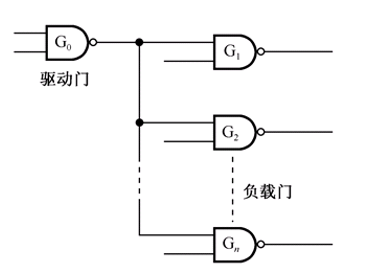
image.png

延迟特性

以与非门为例，在输入端加上一个正方波，则需经过一定的时间间隔才能从输出端得到一个负方波。
image.png

功耗能性

集成度高则功耗高。
当输出端空载，门电路输出低电平时电路的功耗称为空载导通功耗。
空载功耗还和工作频率有关，频率越高，空载功耗越大。