无符号数和有符号数
无符号数
定义
所谓无符号数即没有符号的数,在寄存器中的每一位均可用来存放数值。
例如
123就是一个无符号数,±123就是一个有符号数,显然无符号数只能表达正数,不能表达复数。
表示范围
无符号的数的表示范围和机器字长有关,如果机器字长为16位,那么无符号数的表示范围就是:0~65535
65535就是216-1。
有符号数
对有符号数而言,符号的“正”、“负”机器是无法识别的,但由于“正”、“负”恰好是两种截然不同的状态,如果用“0”表示“正”,用“1”表示“负”,这样符号也被数字化了,并且规定将它放在有效数字的前面,这样就组成了有符号数。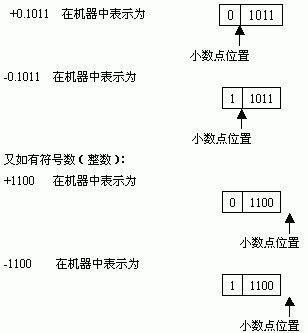
有符号数的表示有三种方式:
如果是小数:
[0.1101]原 = 0.1101
[-0.1101]原 = 1.1101
使用
**.**作为间隔,并且把原先整数位的**0**改为了符号位。
原码中有一个特殊例子,那就是**0**的源码。
由于0可以表示为﹢0和﹣0,所以0的源码有两种:
﹢0:0,0﹣0:1,0
如果机器中采用原码做运算,会出现如下问题:
当一个正数加上一个负数的时候,符号位有可能为正也有可能为负。
相当于做了减法运算,但是计算机不擅长做减法而是擅长加法,所以需要进行一个转换。
补码
补码的本质其实就是同余。
举个例子,在时钟的背景下,如果想要把6点变为3点,有两种做法:
- 6 - 3 = 3
- 6 + 9 = 15 = 3
15点相当于3点。
所以这里6加9和减去3的效果是一样的。
补码的定义如下:
小数补码:
有一种更简单的方法求解:
- 对于正数x:[x]原 = [x]补
- 对于负数x:[x]**补 = [x]原**符号位不变,各位取反,末位加一
例如:
- [1101]补=[1101]原 = 0,1101
- [-1101]补 = 1,0011
负数求解过程如下: 首先求解原码:[- 1101]原 = 1,1101 除了符号位
1,后面四位取反:1,0010 最后末位一个数加一1,0011 如果遇到算数溢出,则舍去溢出部分。
和原码不同的是,±0的补码都是相同的,以4位为例:
- [+ 0000]补:0,0000
- [ - 0000]补:0,0000
- 0000的原码是1,0000
各位取反为:1,1111
末尾加1会发现此时变为了10,0000
这里会发现符号位溢出了,需要去掉最高位,所以
[-0000]补:0,0000
- 0000的原码是1,0000
各位取反为:1,1111
末尾加1会发现此时变为了10,0000
这里会发现符号位溢出了,需要去掉最高位,所以
最后补充一个知识点:
相反数的补码:连同符号位,各位取反,末位加一
假设[y]补 = y0.y1y2...yn,求[-y]补
反码
定义: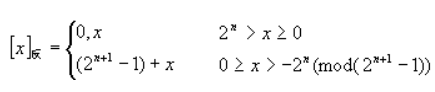
小数定义: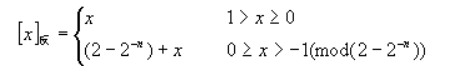
求解很简单:
- 正数:等同于原码
- 负数:符号位不变,各位取反
例如:
- [1101]反=[1101]原 = 0,1101
- [-1101]补 = 1,0010
移码
当真值使用补码表示的时候,由于符号位和数值部分一起编码,所以比较的时候很难从补码的形式上判断真实的大小。
例如数21对应二进制的补码就是:0,10101-21对应二进制的补码表示是:1,01101
由于在计算机中,,其实是不存在的,只是为了便于辨别符号和真值才写的,所以符号位也是一个二进制数,从代码形式上来看,就会得出1,01101 > 0,10101。
但实际是相反的,为了便于直接进行比较,所以出现了移码。
移码的定义是在对应真值加上一个2n。
但是这里有一个更简单的方法计算:对应补码符号位取反
例如:
- [10101]补 = 1,10101
- [-10101]补 = 0,01011
小结
计算机三种码制:
正数:[x]原 = [x]补= [x]反
负数:
- 补 = [x]原 符号位不变,各位取反,末尾加一
- 反 = [x]原 符号位不变,各位取反
正数使用,区分,小数使用.区分。
表示范围:(假设机器字长为8位,总共可以表示256个数)
- 原码:-127 ~ 127
- 补码:-128 ~ 127
- 反码:-127 ~ 127
- 真值: 0 - 255
本小节参见:
福建师范大学网络教育学院网络课程《计算机组成原理》WEB教程
数的定点表示和浮点表示
定点表示
所谓定点表示,就是小数点的位置是固定。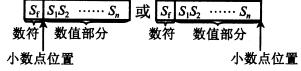
当小数点位于数符和第一数值位之间时,机器内的数为纯小数;
当小数点位于数值位之后时,机器内的数为纯整数。
在定点机中,由于小数点的位置固定不变,故当机器处理的数不是纯小数或纯整数时,必须乘上一个比例因子,否则会产生“溢出”。
比如机器字长为8位,使用定点表示
4这个数就是0000100使用定点表示0.5这个数就是0.10000000(小数点后面8位) 简单来说定点数就是保证位数固定不变。
浮点表示
定义
常用的科学计数法:
352.47=3.5247×102
=3524.7×10-1
=0.35247×103
浮点表示也是类似的,其格式如下:
N=S×rj
其中:
N:真值S:尾数(可正可负)r:基数(一般取 2,4,8)j: 阶码(可正可负)
举个例子:
11.0101 = 0.110101 2*10
注意:这里的
**10**不是十进制当中的十,而是二进制表示的**2**。
S:0.110101r:2-
浮点数的表现形式
浮点数的表现形式如下:
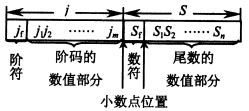
前j位用于表示阶码,其中1位表示阶符(1表示-,0表示+),剩下用于表示真值;
后s位用于表示尾数,其中1位表示数符(1表示-,0表示+),剩下用于表示真值;
举个例子,假设阶码有**4**位,尾数有**8**位,0.110101 * 2**10**可以表示为:
0,010; 0.1101010 阶符:0(1位)阶码真值:010(3位)数符:0(1位)尾数真值:.1101010(7位)使用
**;**间隔尾数和阶码 其中:当小数点后面第一位为1的时候,这种为浮点数的规格化形式。 例如:N = 0.110101 * 210
浮点数的表示范围
以通式N= S×rj为例,设浮点数阶码的数值位取m位,尾数的数值位取n位,当浮点数为非规格化数时,它在数轴上的表示范围如下所示。
首先看正数区,也就需要求出最大正数和最小正数即可确定范围。
如果是最大正数,那么阶码就应该取正数的最大值,m位数值为阶码代表阶码数值的最大值应该为2m-1。
例如:阶码数值为有4位,那么最大值应该是
1111也就是15 = 24 -1
其次,尾数也要最大,也就是尾数数值部分应该全为1,数值部分总共有n位,那尾数的最大值就是1-2-n
例如:尾数数值有8位,那么最大值应该是
0.11111111也就是1-2-8
所以得出了正数区的上限就是:
其余上下限同理可以获得。
浮点数的数值只有在这两个区间(负数区和正数区)之间是有效的,超出这两个区域的都被称为溢出。
**上溢出**:浮点数阶码大于最大阶码,机器停止运算,进行中断溢出处理**下溢出**:浮点数阶码小于最小阶码,尾数强置为0,按照机器零处理浮点数的规格化
在浮点数中:基数r越大,表示的浮点数范围越大,但是精度会下降。
为了提高精度,一般会把尾数转为规格化数,通常通过修改阶码并且将尾数左右移动的方式实现,实现规则如下:基数为2时
- 尾数最高位为1的数是规格化数
左规:尾数左移1位,阶码减1右规:尾数右移1位,阶码加1
- 基数为4时
- 尾数最高2位不全为0的数是规格化数
左规:尾数左移2位,阶码减1右规:尾数右移2位,阶码加1
- 基数为8时
- 尾数最高3位不全为0的数是规格化数
左规:尾数左移3位,阶码减1右规:尾数右移3位,阶码加1注意这里的左移指的是尾数左移,实际小数点是右移的。 例如:0.0010变为0.0100就是左移1位
举例说明
例:将十进制数+13/128写成二进制定点数和浮点数(数值部分取10位,阶码部分取4位,阶符和数符各取1位),分别写出它在定点机和浮点机中的机器数形式。
这里只要知道
1/128就是2-7即可,记得知道+13/128 = 1101 * 2-7
解:令x=+13/128
其二进制形式:x=0.0001101000
定点数形式:x=0.0001101000
定点数不足的位数使用0补齐,小数后面补0,整数前面补0。
浮点数规格化表示:x=0.1101000000×2-11
浮点数的表示可以根据定点数来写,对定点数进行规格化。
定点机中 [x]原=[x]补=[x]反=0.0001101000
浮点机中 [x]原:1,0011;0.1101000000
[x]补:1,1101;0.1101000000
定点数和浮点数的比较
(1)当浮点机和定点机中的数其位数相同时,浮点数的表示范围比定点数大得多。
(2)当浮点数为规格化数时,其精度远比定点数高。
(3)浮点数运算要分阶码部分和尾数部分,而且运算结果都要求规格化,故浮点运算步骤比定点运算步骤多,运算速度比定点低,运算线路比定点复杂。
(4)在溢出的判断方法上,浮点数是对规格化数的阶码进行判断,而定点数是对数值本身进行判断。如小数定点机中的数其绝对值必须小于1,否则即“溢出”,此时要求机器停止运算,进行处理。为了防止溢出,上机前必须选择比例因子,这个工作比较麻烦,给编程带来不便。而浮点数的表示范围远比定点数大,仅当“上溢”时机器才停止运算,故一般不必考虑比例因子的选择。
IEEE754标准
在IEE754浮点数标准中,定义的浮点数的格式如下表所示。
| 浮点数 | 符号位 | 阶码 | 尾数 | 总位数 |
|---|---|---|---|---|
| 短实数 长实数 临时实数 |
1 1 1 |
8 11 25 |
23 52 64 |
32 64 80 |
在IEEE754标准里面:
- 阶码使用移码表示
- 尾数用补码表示
这样做的目的是机器零的表示正好可以让所有的位都是
**0**,便于机器判断。
参见
本小节参见:
福建师范大学网络教育学院网络课程《计算机组成原理》WEB教程
定点运算
移位运算
什么是移位运算
举个简单的例子:15m = 1500cm
这就代表了15这个数字左移了2两位,左移之后空缺的地方补上了0,这就是移位运算。
在十进制中,左移一位,相当于数值大小为原来的10倍,那么在二进制中,左移一位,相当于数值大小为原来的2倍。
前面我们知道,计算机中有些二进制数是代表符号位的,那么又产生如下定义:
| 码 制 | 添补代码 | |
|---|---|---|
| 正数 | 原码、补码、反码 | 0 |
| 负数 | 原码 | 0 |
| 补码 | 左移添0 | |
| 右移添1 | ||
| 反 码 | 1 |
在算数移位的过程中:符号位不参与移动。
举个例子:
设机器数字长为8位(含一位符号位),若A=±26,写出三种机器数左、右移一位和两位后的表示形式及对应的真值,并分析结果的正确性。
首先来看正数,根据八位的字长写出其二进制形式0,0011010:
| 移位操作 | 机 器 数 | 对应的真值 |
|---|---|---|
| [A]原=[A]补=[A]反 | ||
| 移位前 | 0,0011010 | +26 |
| 左移一位 | 0,0110100 | +52 |
| 左移两位 | 0,1101000 | +104 |
| 右移一位 | 0,0001101 | +13 |
| 右移两位 | 0,0000110 | +6 |
红字部分就是补充的
0。 这里会发现黄色背景部分,也就是在右移两位的过程中,由于最后一位1的移除,数据的精度下降了。
接下来看负数,这里就需要根据三种码制的不同来分别分析:
| 移位操作 | 机 器 数 | 对应的真值 | |
|---|---|---|---|
| 移位前 | 原 码 |
1,0011010 | -26 |
| 左移一位 | 1,0110100 | -52 | |
| 左移两位 | 1,1101000 | -104 | |
| 右移一位 | 1,0001101 | -13 | |
| 右移两位 | 1,0000110 | -6 | |
| 移位前 | 补 码 |
1,1100110 | -26 |
| 左移一位 | 1,1001100 | -52 | |
| 左移两位 | 1,0011000 | -104 | |
| 右移一位 | 1,1110011 | -13 | |
| 右移两位 | 1,1111001 | -7 | |
| 移位前 | 反 码 |
1,1100101 | -26 |
| 左移一位 | 1,1001011 | -52 | |
| 左移两位 | 1,0010111 | -104 | |
| 右移一位 | 1,1110010 | -13 | |
| 右移两位 | 1,1111001 | -6 |
这里同样是黄色背景为精度丢失,红色字为补足。
总结上述规律:
- 左移可能会导致结果出错(最高位丢失)
- 右移可能会导致结果精度下降(最低位丢失)
硬件实现左移和右移
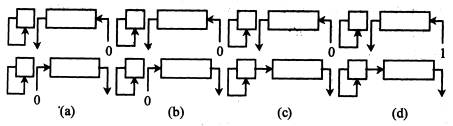
其中(a)真值为正的三种机器数的移位操作;(b)负数原码的移位操作;(c)负数补码的移位操作;(d)负数反码的移位操作。这里有个印象就行。
算数移位和逻辑移位的区别
有符号数的移位称为算术移位,无符号数的移位称为逻辑移位。
逻辑移位的规则是:逻辑左移时,高位移出,低位添0;逻辑右移时,低位移出,高位添0。例如,寄存器内容为01010011,逻辑左移为1010010,算术左移为00100110(最高数位“1”移丢)。
又如寄存器内容为10110010,逻辑右移为01011001。若将其视为补码,算术右移为11011001。显然,两种移位的结果是不同的。
上例中为了避免算术左移时最高数位丢1,可采用带进位(Cy)的移位,其示意图如下图所示。算术左移时,符号位移至Cy,最高数位就可避免移出。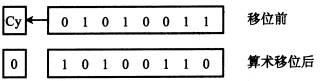
加减法
补码加法的基本公式
前面说过,计算机通常会把减法化为加法进行计算,而把减法化为加法的做法就是使用补码。
加法公式如下:
- 整数:[A]补+[B]补=[A+B]补 (mod 2n+1)
- 小数:[A]补+[B]补=[A+B]补 (mod 2)
减法公式如下:
- 整数:[A-B]补=[A]补+[-B]补 (mod 2n+1)
- 小数:[A-B]补=[A]补+[-B]补 (mod 2)
例题讲解
例:x=0.1010,y=-0.0011,用补码的加法求x+y
解:
[x]补=0.1010,[y]补=1.1101
[x]补+[y]补=0.1010+1.1101=10.0111(溢出部分舍去)
x+y=0.0111
例:x=0.1001,y=-0.0011,用补码的减法求x-y
解:
[x]补=0.1001,[y]补=1.1101,[-y]补=0.0011
[x]补-[y]补=[x]补+[-y]补=0.1001+0.0011=0.1100
x-y=0.1100
溢出判断
例如在上面的题目中,补码做加减法的时候可能会存在溢出现象,这种溢出判断会影响实际值的大小,也就是超出了机器字长表示的范围。所以需要做溢出判断。
判断方式有两种:
(1)用一位符号做溢出判断
不难知道,只有如下两种情况才可能出现溢出:
- 正数+正数
- 负数+负数
减法统一化为加法。
如果出现溢出现象,那么A``B两位的符号位应该是相同的,当运算结果的符号位和原**A**``**B**符号位不同的时候,就是溢出。
例如:书上P239页的表
绝对不是因为我懒得写表所以才让你们看书的。
(2)用两位符号做溢出判断
原始的符号位定义如下:
- 正:
0 - 负:
1
两位符号位的定义如下:
- 正:
00 - 负:
11
同样,如果出现溢出现象,那么A``B两位的符号位应该是相同的。
这种带有两位符号位的补码叫做变形补码,变形补码的运算需要带上符号位。
变形补码判断溢出的原则是:运算结果的两位符号位不同的时候,就表示溢出,否则就是不溢出。
- 正溢出:两位符号位为
01 - 负溢出:两位符号位为
10
无论是否溢出,两位符号位的最高位表示变形补码的真正符号。
例:
设x=+1100,y=+1000,求6位双符号位补码之和[x+y]补。
解:
[x]补=00,1100, [y]补=00,1000
[x+y]补=00,1100+00,1000=01,0100
[x+y]补=01,0100,其中两个符号位出现01,表示已溢出,并且为上溢出,最终结果符号为正。
验算可得:x+y = 12 + 8 = 20 ,确实为上溢出。
原码乘法
笔算乘法
设A=0.1101,B=0.1011,求A×B。
如果是笔算,可以知道: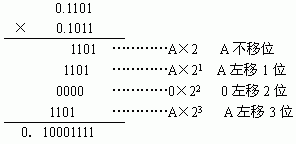
可以看的出来,二进制的乘法其实可以概括为两个运算:加法运算和移位运算。
加法就是加法,而移位运算实际上就是乘2**n**,将其稍作改动可以获得:
由此可以知道原码的计算乘法的方法,主要有两种方法:
- 原码一位乘法
- 原码两位乘法
这里的
**一位**指代的是一次和一位二进制数做运算。 那么两位就是指一次和两位二进制数做运算。
原码一位乘运算
在计算机中,乘法最后的结果不是有一块单独的寄存器存储的,而是分为两块:ACC(乘积高位),MQ(乘积低位)。
详情可以了解一下第一章的内容。
用一到例题来分析一下:
**|x|**表示被乘数的真值。
步骤如下:
- 首先,符号位由乘数和被乘数的符号位做异或决定,不参与后面的真值运算。
- 高位部分首先置为0,低位部分为
**乘数真值** - 然后
**被乘数**依次乘以**乘数**各位(从低位到高位),其结果加上前一次高位部分的结果,作为高位的最终结果 - 高位部分右移一位,移出的部分补到低位部分的高位,低位部分的最低位舍去(这一点非常重要)
- 往复上述过程,直到乘数所有位数都被乘完,最终高位和低位合并即为最终结果。
比如,一开始高位置为0,也就是00.0000,低位为乘数真值,也就是1011。
先做加法运算,被乘数1101乘以乘数最低位1答案就是1101,结果加上前一次高位就是00.1101。
接下来做移位运算,高位右移一位:00.0110**~~1~~**;低位右移并且补位:**1**110**~~1~~**。
原码两位乘运算
原码两位乘与原码一位乘一样,符号位的运算和数值部分是分开进行的,但原码两位乘是用两位乘数的状态来决定新的部分积如何形成,因此可提高运算速度。
思路还是和一位乘一样,一位乘每次值乘一个二进制位数,也就是只有0, 1,两位乘就有四种情况:
| 乘数 | 新的部分积 |
|---|---|
| 0 0 | 加上0倍的|x| |
| 0 1 | 加上1倍的|x| |
| 1 0 | 加上2倍的|x| |
| 1 1 | 加上3倍的|x| |
上面四种情况里面,0倍就是加上0,1倍就是加上原数,2倍相当于原数直接左移一位,只有3倍处理起来比较麻烦,在计算机中可以这样操作:原数先乘以4(左移两位),再减去1倍的原数(转为补码就变成了加法)。
补码乘法
补码一位乘运算
补码做乘法运算的时候,大致和原码运算相同,以小数为例,假设:
**被乘数**:[x]补 = x0.x1x2…xn**乘数**:[y]补 = y0.y1y2…yn原始一位乘不常用,看一下例题即可
补码一位乘法披着虎皮的汤姆猫的博客-CSDN博客补码一位乘法
补码比较法
常用的补码一位乘运算有:Booth算法。
手算模拟过程如下:
重点注意的上图中低位部分的末尾(yi)和辅助位(yi+1初始值为0):
yi |
yi+1 |
操作 | 说明 |
|---|---|---|---|
| 0 | 0 | +0 | 处于0串中,不需要操作 |
| 0 | 1 | +[x]补 | 1串的结尾 |
| 1 | 0 | -[x]补 | 1串的开始 |
| 1 | 1 | +0 | 处于1串中,不需要操作 |
运算过程大致如原码乘法,从上面的图中可知,**4位真值**的补码一位乘法运算,一共做了:
- 4次移位运算
- 5次加法运算
最后一次加法运算和yi无关,统一加上**[x]****补**是用于矫正。
比较一下原码乘法运算:
| 原码一位乘法: | 补码一位乘法: |
|---|---|
| 进行 n 轮加法、移位 | 进行 n 轮加法、移位,最后再多来一次加法 |
| 每次加法可能 +0、+[|x|]原 | 每次加法可能 +0、+[x]补、+[-x]补 |
| 每次移位是“逻辑右移” | 每次移位是“补码的算数右移” |
| 符号位不参与运算 | 符号位参与运算 |
参见:
补码乘法运算(计算机组成原理18)挚爱FXJ的博客-CSDN博客补码乘法
除法运算
笔算除法分析
笔算除法如下:
和正常十进制的除法运算类似,特点可以归纳为:
- 每次
**上商**都是通过比较余数(被除数)和除数的大小来确定商为1还是0。- 例如:第一步中
0.1101作为除数,大于被除数0.1011,所以第一位上商为0
- 例如:第一步中
- 每一次做减法运算,余数(被除数)不动,低位补
0,再减去右移后的除数。 - 上商的位置不固定(说实话我也不懂这句话是什么意思)
**商符**单独处理(也就是做异或运算)小数定点除法运算对于被除数和除数有一定的约束:0 < |被除数| ≤ |除数|
原码除法
原码除法有两种方法:
- 恢复余数法
- 加减交替法
假设:
(1)恢复余数法
特点:当余数为负数的时候,加上除数,让余数恢复为原来的余数。
步骤:
- 符号位单独按两数符号异或求得;参与运算的是绝对值的补码
- 判溢出, 要求|被除数| < |除数| (对小数而言)(如果是整数,则要求|被除数| > |除数| );
- 被除数减去除数,(加上除数的补码)
- 若所得余数为正,相应位上商为1,余数左移一位,减去[y]补;若余数为负,相应位上商为0,余数加上除数(恢复余数),再左移一位,加上[-y]补;
- 重复第4步,直到求得所要求的商为止(移n次)
- 若最后一步余数为负,则需要恢复余数。
举个例子:
例:已知:x=-0.1011,y=-0.1101,求:[x÷y]原
解:首先写出x和y的原码补码:[x]原=1.1011,[-y]补=1.0011,[y]原=1.1101
| 被除数(余数) | 商 | 说 明 |
|---|---|---|
| 0.1011 + 1.0011 |
0.0000 | +[-y*]补(减去除数) |
| 1.1110 + 0.1101 |
0 | 余数为负,上商0 恢复余数+[y*]补 |
| 0.1011 1.0110 + 1.0011 |
0 | 被恢复的被除数 左移1位 +[-y*]补(减去除数) |
| 0.1001 1.0010 + 1.0011 |
01 01 |
余数为正,上商1 左移1位 +[-y*]补(减去除数) |
| 0.0101 0.1010 +1.0011 |
011 011 |
余数为正,上商1 左移1位 +[-y*]补(减去除数) |
| 1.1101 + 0.1101 |
0110 | 余数为负,上商0 恢复余数+[y*]补 |
| 0.1010 1.0100 + 1.0011 |
0110 | 被恢复的被除数 左移1位 +[-y*]补(减去除数) |
| 0.0111 | 01101 | 余数为正,上商1 |
符号位由除数和被除数决定,最后可得,商值为0.1101。
四位小数,做
五次加法运算,其中最后一次为矫正作用。
(2) 加减交替法
所谓渐渐交替法,也就是不做余数的回复,通过先移位的方式来避免恢复余数,过程如下:
举个例子:
例:已知:x=0.1011,y=-0.1101,求:[x÷y]原
解:首先写出x和y的原码补码:[x]原=1.1011,[-y]补=1.0011,[y]原=1.1101
这里是无论上商为多少,都是先做移位运算,再根据上商做加法
- 上商0:+[y*]补
- 上商1:+[-y*]补
| 被除数(余数) | 商 | 说 明 |
|---|---|---|
| 0.1011 + 1.0011 |
0.0000 | +[-y*]补(减除数) |
| 1.1110 1.1100 + 0.1101 |
0 0 |
余数为负,上商0 ← 1位 +[y*]补 (加除数) |
| 0.1001 1.0010 + 1.0011 |
01 01 |
余数为正,上商1 ← 1位 +[-y*]补(减除数) |
| 0.0101 0.1010 + 1.0011 |
011 011 |
余数为正,上商1 ← 1位 +[-y*]补(减除数) |
| 1.1101 1.1010 + 0.1101 |
0110 0110 |
余数为负,上商0 ← 1位 +[y*]补 (加除数) |
| 0.0111 | 01101 | 余数为正,上商1 |
补码除法
补码除法常采用加减交替法。
算法规则如下:
- 符号位参加运算,除数与被除数均用双符号补码表示。
- 被除数与除数同号,被除数减去除数;被除数与除数异号,被除数加上除数。
- 余数与除数同号,商上1,余数左移一位减去除数; 余数与除数异号,商上0,余数左移一位加上除数。(注意:余数左移加上或减去除数后就得到了新余数。)
- 采用校正法包括符号在内,重复n+1次3
注意,使用此运算规则,需要修正商符,商的末位恒置1。
简化可得:
| [x]补与[y]补 | 商值 |
|---|---|
| 同号 | 1 |
| 异号 | 0 |
关于商符:
在小数定点除法中,被除数的绝对值必须小于除数的绝对值,否则商大于1而溢出。因此:
- 当[x]补与[y]补同号时,[x]补-[y]补所得的余数[R0]补与[y]补异号,商上“0”,恰好与商的符号(正)一致;
- 当[x]补与[y]补异号时,[x]补+[y]补所得的余数[R0]补与[y]补同号,商上“1”,这也与商的符号(负)一致。
可见,商符是在求商值过程中自动形成的。
此外,商的符号还可用来判断商是否溢出。例如:
- 当[x]补与[y]补同号时,若[R0]补与[y]补同号,上商“1”,即溢出。
- 当[x]补与[y]补异号时,若[R0]补与[y]补异号,上商“0”,即溢出。
当然,对于小数补码运算,商等于“-1”应该是允许的,但这需要特殊处理,为简化问题,这里不予考虑。
举个例子:
例:已知:x=-0.1001, y=+0.1101 求: [x÷y]补
解:[x]补=1.0111,[y]补=0.1101,[-y]补=1.0011
| 被除数(余数) | 商 上商 | 说 明 |
|---|---|---|
| 1.0111 + 0.1101 |
0.0000 | [x]补与[y]补异号,+[y]补 |
| 0.0100 0.1000 + 1.0011 |
1 1 |
[R]补与[y]补同号,上商1 ← 1位 +[-y]补 |
| 1.1011 1.0110 + 0.1101 |
10 10 |
[R]补与[y]补异号,上商0 ← 1位 +[y]补 |
| 0.0011 0.0110 + 1.0011 |
101 101 |
[R]补与[y]补同号,上商1 ← 1位 +[-y]补 |
| 1.1001 1.0010 |
1010 10101 |
[R]补与[y]补异号,上商0 ← 1位,末位商恒置“1” |
参照
本小节参见:
原码、补码的除法运算yyyloki的博客-CSDN博客原码除法
福建师范大学网络教育学院网络课程《计算机组成原理》WEB教程
浮点四则运算
浮点加减运算
首先我们需要知道浮点数的形式:
x = S r j
由于浮点数尾数的小数点均固定在第一数值位前,尾数的加减运算规则与定点数完全相同。但由于其阶码的大小又直接反映尾数有效值的小数点位置,因此当两浮点数阶码不等时,因两尾数小数点的实际位置不一样,尾数部分无法直接进行加减运算。因此,浮点数加减运算必须按以下n步进行:
①对阶:使两数的小数点位置对齐。
②尾数求和:将对阶后的两尾数按定点加减运算规则求和(差)。
③规格化:为增加有效数字的位数,提高运算精度,必须将求和(差)后的尾数规格化。
④舍入:为提高精度,要考虑尾数右移时丢失的数值位。
⑤*判断结果:即判断结果是否溢出。
对阶
对阶的目的是使两操作数的小数点位置对齐,即使两数的阶码相等。为此,首先要求出阶差,再按小阶向大阶看齐的原则,使阶小的尾数向右移位,每右移一位,阶码加1,直到两数的阶码相等为止。右移的次数正好等于阶差。尾数右移时可能会发生数码丢失,影响精度。
例如,两浮点数x=0.1101×201,y=(-0.1010)×211,求x+y。
很明显这里y的阶码比较大,所以这里需要转换的是x的阶码,由01变为11,也就是从1变成了3,尾数应该右移两位,所以0.1101变为0.0011。此时x=0.0011×211。
尾数求和
将对阶后的两个尾数按定点加(减)运算规则进行运算。
如上例中的两数对阶后得:
[x]补=00,11;00.0011
[y]补=00,11;11.0110
则[Sx+Sy]补=00.0011+11.0110=11.1001
即[x+y]补=00,11;11.1001
规格化
由第二章可知,尾数S的规格化形式为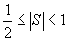
如果采用双符号位的补码,则
- 当S>0时,其补码规格化形式为:[S]补=00.1××…×
- 当S<0时,其补码规格化形式为:[S]补=11.0××…×
对S<0时,有两种情况需特殊处理。
①S=-1/2,则[S]补=11.100…0。对于补码而言,它不满足于上面的规格化表示式。为了便于硬件判断,特规定-1/2是规格化的数(对补码而言)。
②S=-1,则[S]补=11.000…0。因小数补码允许表示-1,故**-1**视为规格化的数。
规格化又分左规和右规两种。
(1)左规。当尾数出现00.0××…×或11.1××…×时,需左规。左规时尾数左移一位,阶码减1,直到符合补码规格化表示式为止。
如上例求和结果为6
[x+y]补=00,11;11.1001
尾数的第一数值位与符号位相同,需左规,即将其左移一位,同时阶码减1,得[x+y]补=00,10;11.0010。
(2)右规。当尾数出现01.××…×或10.××…×时,表示尾数溢出,这在定点加减运算中是不允许的,但在浮点运算中这不算溢出,可通过右规处理。右规时尾数右移一位,阶码加1。
舍入
在对阶和右规的过程中,可能会将尾数的低位丢失,引起误差,影响了精度,为此可用舍入法来提高尾数的精度。常用的舍入方法有三种。
(1)截去法:将多余的位截去,剩下的位不变。其最大误差接近于数据最低位上的1。
特点:有舍无入,具有误差积累。
(2)“0舍1入”法:“0舍1入”法类似于十进制运算中的“四舍五入”法,即在尾数右移时,被移去的最高数值位为0,则舍去;被移去的最高数值位为1,则在尾数的末位加1。这样做可能使尾数又溢出,此时需再做一次右规。
特点:其最大误差是最低位上的-1/2到接近于1/2之间,正误差可以和负误差抵消。是比较理想的方法,但实现起来比较复杂。
(3)“恒置1”法:尾数右移时,不论丢掉的最高数值位是“1”或“0”,都使右移后的尾数末位恒置“1”。这种方法同样有使尾数变大和变小的两种可能。
特点:尽管误差范围扩大了,但正负误差可以相互抵消,从统计角度,平均误差为0。因此最后运算结果的准确性提高了。
判断溢出
- 阶码[j]补=01,××…×为上溢。
- 阶码[j]补=10,××…×为下溢,按机器零处理。
阶符为“01”时,需做溢出处理。
完整运算
浮点乘除运算
两个浮点数相乘,其乘积的阶码应为相乘两数的阶码之和,其乘积的尾数应为相乘两数的尾数之积。
两个浮点数相除,商的阶码为被除数的阶码减去除数的阶码,其尾数为被除数的尾数除以除数的尾数所得的商。
步骤如下:
- 阶码运算
- 尾数运算
- 规格化
运算规则同定点数运算,看例题即可:
乘法运算: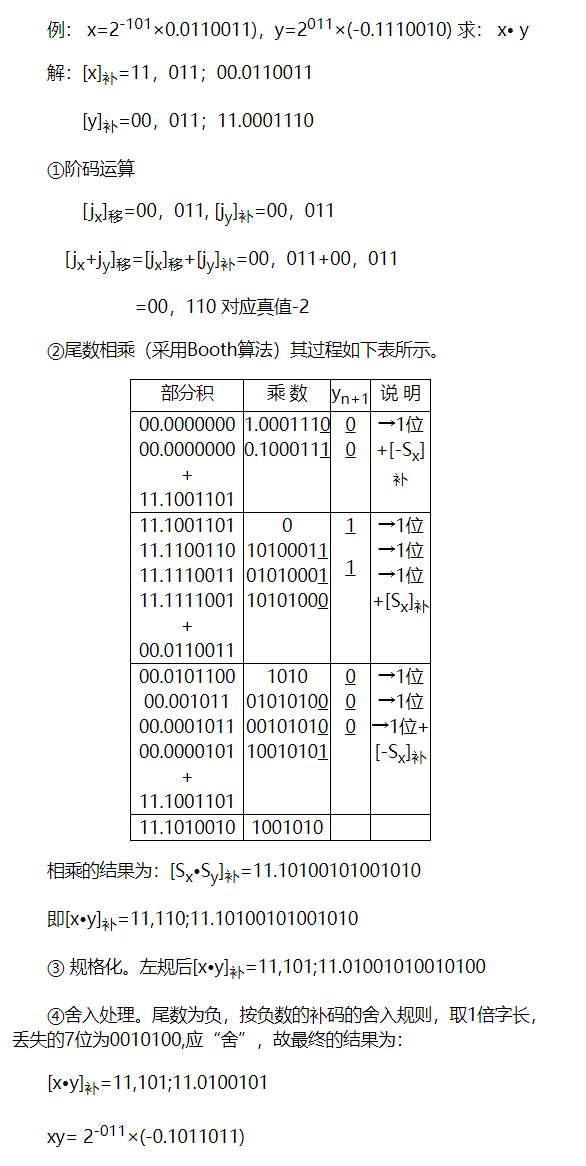
除法运算: