7.1 查找的相关定义和概念

查找表(Search Table) ：由同一类型的数据元素(或记录)构成的集合。
对查找表经常进行的操作:

  1. 1）查询某个“特定的”数据元素是否在查找表中；
  2. 2）检索某个“特定的”数据元素的各种属性；
  3. 3）在查找表中插入一个数据元素；
  4. 4）从查找表中删去某个数据元素。

静态查找表(Static Search Table) :仅做上述1）和2）操作的查找表
动态查找表(Dynamic Search Table):做上述1）、2）、3）、4）操作的查找表

上述定义了解即可。

关键字(Key):数据元素中某个数据项的值，用以标识一个数据元素。
查找算法的性能分析：通常以关键字和给定值进行比较的记录个数的平均值为衡量算法好坏的依据.
平均查找长度(Average Search Length)：查找算法在查找成功时平均查找长度和查找不成功时平均查找长度之和。

一般情况下只会计算查找成功的平均查找长度。

为了计算查找长度我们定义如下概念：

  • Pi:查找表中第i个记录的概率（一般都是取1/n）
  • Ci:找到表中其关键字与给定值相等的第i个记录时，和给定值比较过的关键字的个数．
  • ASLSS：查找成功的平均查找长度
  • ASLSF：查找失败的平均查找长度
  • ASL：平均查找长度（成功的+失败的）

不难得出如下公式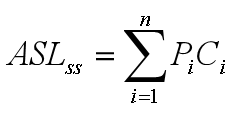
image.png
为了方便之后的算法分析这里引入一个宏定义

  1. 关键字比较宏定义
  2. #define EQ(a,b)  ((a)==(b))
  3. #define LT(a,b)  ((a)<(b))
  4. #define LQ(a,b)  ((a)<=(b))

这边的宏定义就是用来比较传入参数ab的大小 返回值是boolean类型，如果传入的参数符合宏定义，那么返回true，反之则为false。 一般情况下ab参数的类型都是int

7.2 顺序表的查找

顺序查找

特点

适用场合：以顺序表表示静态查找表，表内元素无序。
思想：从表中最后一条记录起，逐个比较记录关键字与给定值，若相等查找成功；反之，直至与第一条记录不等，查找不成功

性能分析

不难得出第i个元素被查找成功的相关数据为：

  • Pi=1/n
  • Ci=n-i+1

所以ASLSS=(n+1)/2。

上述的查找成功的平均查找长度记住即可，推导可以自行推导。

  • 顺序查找的缺点：平均查找长度大，n越大，效率越低。
  • 顺序查找的优点：算法简单，适用面广；不关心记录是否有序。

    由于过于简单这里就不举例子了。

折半查找/二分法查找（重点）

这里先把最重要的一点提出来：
前提：需要被查找的表一定要是一个有序列表。
方法：

  • 设定查找范围的下限low，上限high，由此确定查找范围的中间位置mid；
  • 中间位置的值等于待查的值，查找成功
    • 中间位置的值小于待查的值，low=mid+1
    • 中间位置的值大于待查的值，high=mid-1
  • 直到low>high，查找失败。

【查找】折半查找秃头仔仔-安凯雯的博客-CSDN博客折半查找

判定树

个人认为不大会考，所以看
折半查找判定树的画法（较简单易懂！）Smoothzjc的博客-CSDN博客折半查找判定树怎么画
就可以了，不会我觉得问题也不大。

性能分析

ASLSS=((n+1)/n)(log2(n+1))-1

当n比较大的时候一般都习惯写成ASLSS=log2(n+1) - 1

  • 折半查找优点：效率高于顺序查找
  • 折半查找缺点：适用面窄仅适用于有序顺序表,且采用顺序存储结构

索引查找（不要求掌握）

索引顺序查找（分块查找）：顺序表＋索引表组成
应用范围：有序或分块有序的顺序表。
分块有序：第二个子表中的所有记录的关键字都大于第一个子表的最大关键字，依次类推。
image.png
查找时现在索引表中进行查找，比较得出44在22和48中间
所以得出44的地址应该在7-12之间

因为44比第一个区块的最大值22还大，但是又小于第二个区块最大值48，所以44只能在第二个区块之中 而第二个区块的地址范围就是7-12

之后再到第二个区块中进行顺序查找即可。

性能分析：

设长度为n的表均匀分成b块，每块含有s个记录，b=n/s，
每块查找概率1/b，块中每个记录的查找概率是1/s。
则 ASLbs=Lb+Lw，

  • Lb:索引表确定所在块的平均查找长度。
  • Lw:块中查找元素的平均查找长度。
    • 索引表、顺序表皆顺序查找： 　

image.png
当 s =sqrt(n) 时，ASL取极小值sqrt(n) + 1

  • 索引表二分查找、顺序表顺序查找：

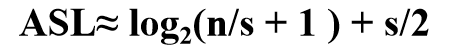
image.png

7.3 动态查找表

二叉排序树

定义

具有以下性质的二叉树被叫做二叉排序树

  • 根的左子树若非空，则左子树上的所有结点的关键字值均小于根结点的值。
  • 根的右子树若非空，则右子树上的所有结点的关键字值均大于根结点的值。
  • 它的左右子树同样是二叉排序树。

举个例子：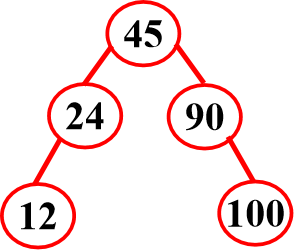
image.png
它的结构体定义也很简单：

  1. typedef struct BSTNode{
  2.   ElemType data;
  3.   struct BSTNode *lchild,*rchild;
  4.  }BSTNode,*BSTree;

一个数据域用来标识这个结点的数值，两个指针域来指向左右子树。

查询算法

查找方法主要靠递归函数，这个也很简单：
首先看递归的终止条件：

  1.  T==NULL||EQ(key,T->data.key)

其中T表示的是结点，所以当结点T为NULL值的时候表示查找失败，或者当结点T的数据值的大小等于需要查找的key的值的时候表示查找成功。

回顾一下这里的EQ()是一个宏定义，表示判断括号里面的两个数是否相等。

递归的步骤也很简单

  1. if(key<T->data.key) Search(T->lchild,key) 
  2. if(key>T->data.key) Search(T->rchild,key)

解释一下：
就是当结点T的值大于key的时候就搜索左子树（因为左子树的值都小于根节点的值）
就是当结点T的值小于key的时候就搜索右子树（因为左子树的值都大于根节点的值）

整体算法

  1. Status SearchBST ( BSTree T,KeyType key){
  2. /*在二叉排序树查找关键字值为key的结点。若查找成功返回指向该数据元素结点的指针，否则返回空指针*/
  3.     if((!T) || EQ(key,T->data.Key)) 
  4.         return T;
  5.     else if(LT(key,T->data.key))
  6.         return (SearchBST(T->lchild,key));
  7.     else 
  8.         return (SearchBST(T->rchild,key)); 
  9. } // SearchBST

插入算法

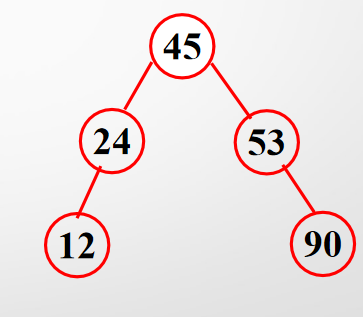
image.png
以上面这张图为例：序列45、24、53、12、90构成一棵二叉排序树
算法如下：

  • 首先定义一个空的二叉排序树，所以树中无节点。
  • 创立一个根节点
  • 把第一个树45赋值给该根节点
  • 接着比较24和45的大小，发现24应该是45的左子树
  • 同理比较53，发现53是45的右子树
  • 12先和45比较，再和24比较发现是24的左子树
  • 同理90是53的右子树

把插入函数抽象出来方法如下：

  • 二叉排序树的存储结构使用链表
  • 首先执行查找算法，找出被插入结点的父亲结点。
  • 若二叉树为空。则首先单独生成根结点。
  • 判断被插结点是其父亲结点的左、右孩子。将结点插入

将查找算法进行修改可得：

  1. 修改后的二叉排序树查找算法
  2. Status SearchBST(BSTree T,KeyType key,BSTree f,BSTree &p)
  3. /*在二叉排序树查找关键字值为key的结点。初始时f为NULL。如T=NULL，则p=NULL,返回FALSE。如T!=NULL且查找成功，p=T,返回TRUE。如T!=NULL且查找不成功，p=f,返回FALSE。f为待插入结点的的双亲结点地址。*/
  4.  { if  ((!T) { p = f; return FALSE; }
  5.    else if (EQ(key,T->data.key)) { p = T; return TRUE; }
  6.    else if (LT(key,T->data.key))
  7.         return (SearchBST ( T -> lchild, key, T, p ));//①
  8.    else 
  9.         return (SearchBST ( T -> rchild, key , T, p )); //②
  10.   } // SearchBST

注意后面两个语句①和语句②，在每次比较后都改变了参数f的值为该结点。 所以当T!=NULL且查找不成功的时候，f才是这个待插入结点的双亲节点

插入算法整体代码

  1. Status Insert BST ( BSTree &T，ElemType e )
  2. // 在二叉排序树中不存在 e.key 时，插入并返回 TRUE，否则返回FALSE
  3.  {  if ( ! SearchBST ( T,e.key,NULL,p) 
  4.     {  s = ( BSTree ) malloc ( sizeof ( BSTNode ) ); 
  5.         s->data = e; s->lchild = s->rchild = NULL;
  6.         if  ( ! p )  T = s; //插入结点是根结点
  7.         else if ( LT( e.key , p ->data. key ) ) p -> lchild = s;
  8.                else p -> rchild = s; 
  9.         return TRUE;
  10. 　}return FALSE;    
  11.   }  // Insert BST

这里就不加解释了 相信大家一定都看得懂

Y3)S`U]03P~R0NC50Y~%X65.jpg

查找分析

查找成功的情况：查找走过一条从根结点到该结点的路径，与关键字比较次数等于路径长度+1，总的比较次数不超过树的深度
查找不成功的情况：查找走过一条从根结点到叶子结点的路径，与关键字比较次数等于路径长度+1，总比较次数不超过树的深度。

举两个例子：
[例1]关键字序列1，2，3，4，5构造一棵二叉排序树
构造后如图所示：
image.png

其中插入1的路径长度为0，那么比较次数就是1 2345以此类推分别是**2、3、4、5** 所以ASL=(1+2+3+4+5)/5 = 3

[例2]关键字序列3，1，2，5，4构造一棵二叉排序树
构造后如图所示：

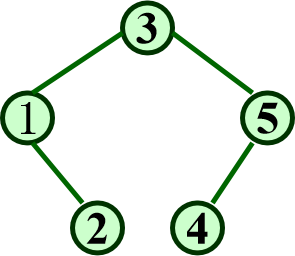
image.png

同上可得 ASL = (1+2+3+2+3)/5=2.2

  • 最坏情况：当插入关键字有序，二叉排序树蜕变成单支树，深度为n，ASL=(n+1)/2
  • 最好情况：二叉排序树与折半查找判定树相同，ASL与log2n成正比。

    7.4 哈希表

    定义

    在记录的关键字和其在表中位置之间建立一种函数关系，即以f(key)作为关键字为key的记录在表中的位置。

    哈希函数是一个映象，将关键字的集合映射到某地址集合(类似于数学中的函数)

相关概念

冲突：不同关键字得到同一哈希地址，key1≠key2，f(key1)=f(key2)
同义词：在一个哈希函数中具有相同函数值的不同关键字。
哈希造表或散列：映象过程。（不重要）
哈希地址或散列地址：所得的存储位置。
构造哈希表要注意的问题：

  • 考虑选择一个“好”的哈希函数;
  • 选择一种处理冲突的方法。

    哈希函数的构造方法

    直接定址法

    取关键字或关键字的某个线性函数值为哈希地址。即H(key)=key或H(key)=a×key＋b。也叫自身函数。

    类似于数学中的一次函数 特点：1.直接定址所得地址集合和关键字集合的大小相同。

    1. 2.不同关键字不会发生冲突。

数字分析法

分析关键字，取其若干位或组合作哈希地址

特点：适于关键字位数比哈希地址位数大，且关键字已知的情况

举个例子：
image.png

平方取中法

取关键字平方后的中间几位为哈希地址。
e.g: （4731）2 ＝223 82 361 ；选取82

特点：适于不知道全部关键字情况

除留余数法

取关键字被某个不大于哈希表长m的数p除后的余数为哈希地址。H(key) = key% p (p≤m)。
(一般p为接近于m的质数和不包含小于20的质因数的合数)

特点：简单常用，可与上述方法结合使用,p选不好易产生同义词

上述四种方法了解即可。

解决冲突的方法

开放定址法（重点！）

Hi=(H(key)+di) %m
其中i=1,2,…,k (k≤m-1)，H(key)为哈希函数值；m：哈希表长，di是增量序列
di有三种取法

  1. di=1,2,…m-1，称为线性探测再散列
  2. di=12,-12,22,-22,…,±k2 (k≤m/2)称为二次探测再散列
  3. di=伪随机数列，称为随机探测再散列

    主要记住前两种取法。

举个例子：

  1. 采用哈希函数H(key)=key % 11,关键字序列为：17,60,29,38。使用线性探测再散列方法处理冲突。

image.png

  1. 首先17%11=6，与地址6比较一次不冲突，（因为不存在值）所以17的地址为6
  2. 60%11=5，与地址5比较一次不冲突，所以所以60的地址为5
  3. 29%11=7，与地址7比较一次不冲突，所以29的地址为7
  4. 38%11=5，此时地址5已经有了17，所以根据公式Hi=(H(key)+di) %m Hi =(5+d**i**）%11

这里di=1、2、3、….、k，
这里先与原来的5比较，冲突，转到下一个与6比较，依旧冲突，继续下一个7比较，还是冲突，一直到8不冲突
所以不断增加可以得出38的最终地址为8

这种在处理冲突过程中发生的两个第一个哈希地址不同的记录争夺同一个后继哈希地址的现象，被称作二次聚集现象

上述例子中不难得出探测时候有如下公式：
比较次数 = 发生冲突次数+1
所以我们计算上述例子中的ASLSS
ASLSS =(1/11)*(1+1+1+4) = 7/11

这里的ASLSS就是所有数所有比较次数之和与平均概率（基本上就是1/m）的乘积


再哈希法（了解即可）

Hi=RHi（key）i=1,2,…,k，RHi和Hi都是不同的哈希函数，在同义词产生地址冲突时计算另一个哈希函数地址。直到冲突不再发生，这种方法不易产生聚集，但增加了计算时间。

公共溢出区法（了解即可）

HashTable[0..m-1]:基本表，每个分量存放一个记录。
OverTable[0..v]:溢出表，所有关键字和基本表中关键字为同义词的记录，填入溢出表。

链地址法

将所有关键字为同义词的记录存储在同一线性链表中
如下图所示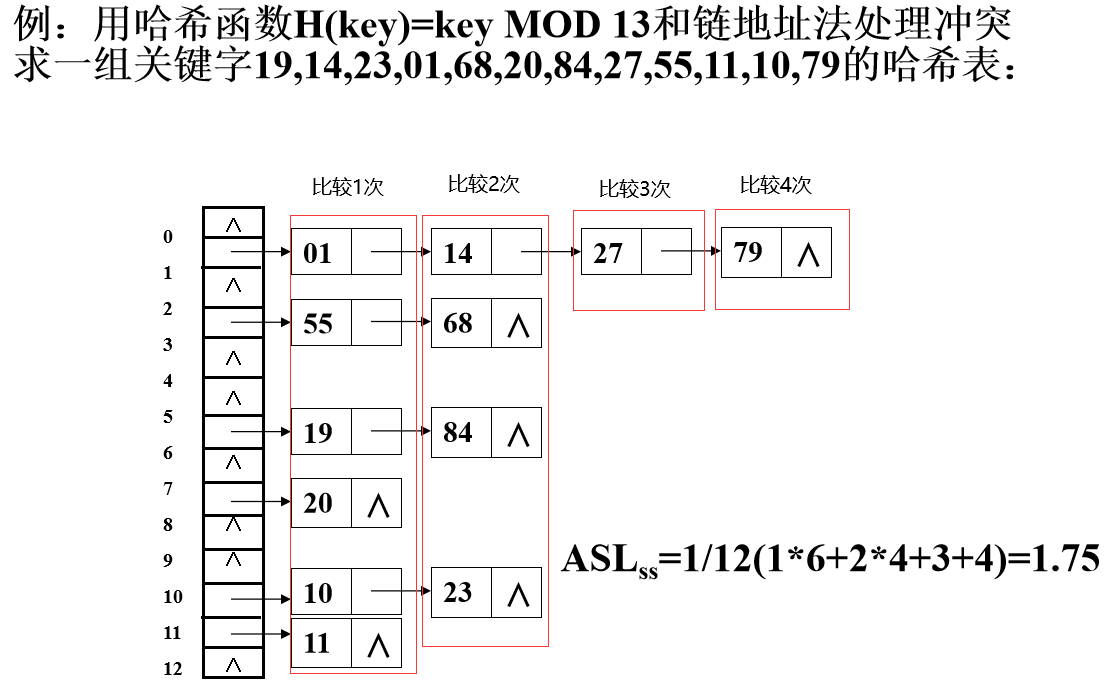
image.png

哈希表的性能分析

image.png