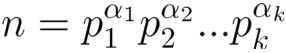第一章：整除

写在前面的话

妹想到啊，都大三了还要学数学呜呜呜。

考核方式

整除的概念和基本性质

整除的定义

设a,b∈Z，a≠0。如果存在某个整数q∈Z，使得b=aq，则称**a**整除**b**或**b**被**a**整除（注意顺序），记为a|b,且称a为b的因数，b为a的倍数。

显然，**0**是任何整数的倍数。对于任意整数a,±1,±a都是它的因数，称这四个因数为整数a的显然因数或平凡因数，整数a的其他因数称为非显然因数或非平凡因数。

整除的性质

1. 如果a|b且b|c，则有a|c
2. 如果a|b且a|c，当且仅当对于任意x,y∈X,有a|bx + cy
3. 设m≠0,a|b当且仅当ma|mb
4. 如果a|b且b|a，则a=±b

   四条性质都需要知道，尤其是第二条。

带余除法

设a,b是两个给定的整数，a≠0，那么一定存在唯一的一对整数q和r，满足：
b=aq+r, 0≤r<|a|
因此，a|b的充要条件是r=0（整除的等价定义）。

这里r就是余数。

公因数

公因数与最大公因数

设a1,a2,d是三个整数，若d|a1,d|a2，则称 是整数d是a1，a2的公因数。对于k个数同理。

设a1,a2是两个不全为零的整数，把a1,a2的公因数中的最大正整数称为整数a1, a2的最大公因数，记为gcd(a**1,a2**)或简记(a1,a2)。对于k个数同理。
当(a**1, a2**)= 1，称a1, a2互素。

最大公因数的性质

对任意整数a,b,c有
(1) 有(a,b)=(b,a)= (-a,b)= (a,-b)
(2) 若a|b ，则(a,b)=|a|
(3) 对于任意两个整数a,b ，必有(a, b)|ax + by
(4) 若a = bq+c ，q是一个整数，则有(a,b)=(b,c)
(5) 若(a, c)=1 ， b|c ，则(a,b)= 1
(6) (a/(a+b),b(a+b)) = 1

公倍数

公倍数与最小公倍数

设a1,a2,l是三个整数，若a1|l,a2|l，则称l是整数a1,a2的公倍数。对于k个数同理。
设a1,a2是两个不全为零的整数，把a1,a2的所有公倍数中的最小正整数称为整数a1,a2的最小公倍数，记为lcm[a1, a2]或简记为[a1,a2]。对于k个数同理。

公倍数的性质

(1) 设a, b, m是整数，a |m, b|m ，则[a,b]|m

欧几里得算法及其扩展算法

辗转相除法（欧几里得算法）

这个算法用于求解给定整数a，b的最大公因数。
利用的核心性质是：若a = bq+c ，q是一个整数，则有(a,b)=(b,c)
算法过程如下：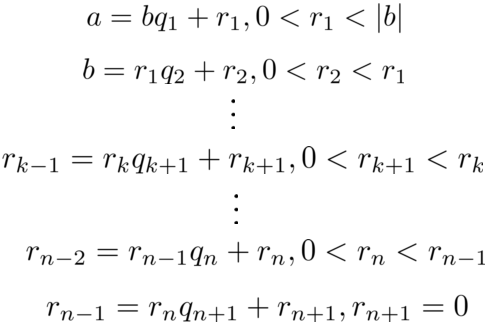

简单来说就是不断用b和b|a的余数r做带余除法。

经过有限步运算，必然存在n使得rn+1= 0，此时rn即为最大公因数。
求解4864 和 3458 的最大公因数。
4864 = 1 × 3458＋1406, q1 = 1,r1= 1406
3458 = 2 × 1406＋ 646， q2= 2,r2= 646
1406 = 2 × 646+114, q3 = 2,r3 = 114
646 = 5 × 114＋76, q4 = 5,r4 = 76
114 = 1 × 76＋38， q5 = 1,r5= 38
76 = 2 × 38 q6= 2,r6= 0
所以，最大公因数为：**38**

如果碰到带有负数求解最大公因数，可以利用性质(a,b)=(b,a)= (-a,b)= (a,-b)转换为对正数的求解。

重要定理

(1) 对于任意两个整数 a,b，存在整数x,y使得：
(a,b) = xa + yb
(1 推论) 设a, b,c为不等于0的整数，若c|a,c|b ，则c|(a,b)。
(2) 设a,b是两个不全为0的整数，则(a,b)=1当且仅当存在整数u,v使得
ua +vb = 1
(3) 设a,b,c为不等于0的整数：
① 若c|ab, (a,c)= 1，则c|b
② 若a|c,b|c且(a,b)=1 ，则ab|c
(4) 设a,b是两个正整数:
① 若a，b互素，则[a,b] = ab
② [a,b] = ab/(a,b) <=> a,b

扩展算法

求解 d =(a,b)与满足ax +by =d的整数x与y：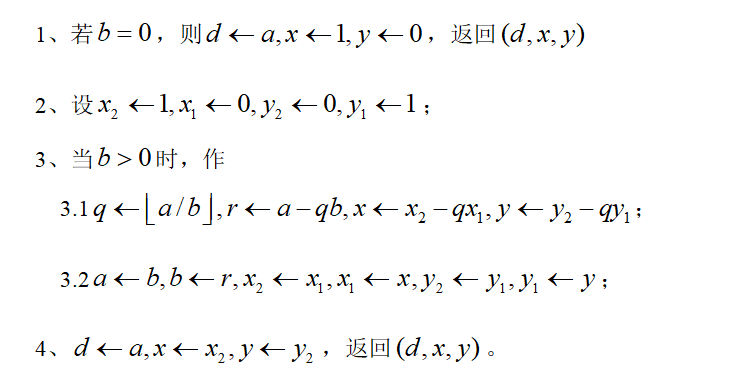

还是举个例子：
求解整数x，y使得(4864,3458) = 4864x + 3458y。
首先还是利用欧几里得算法求解最大公因数：
① 4864 = 1 × 3458＋1406, q1 = 1,r1= 1406
② 3458 = 2 × 1406＋ 646， q2= 2,r2= 646
③ 1406 = 2 × 646+114, q3 = 2,r3 = 114
④ 646 = 5 × 114＋76, q4 = 5,r4 = 76
⑤ 114 = 1 × 76＋38， q5 = 1,r5= 38
⑥ 76 = 2 × 38 q6= 2,r6= 0
易得，最大公因数为38
接下来依次从后往前反向表达最大公因数（从倒数第二个开始）：
38 = 114 - 76 ⑤
= 114 -(646-5×114) ④
= 646 +6 ×(1406 - 2×646) ③
= 6 ×1406 - 13×(3458-2 × 1406) - 13× 3458＋32× (4864 - 3458) ②
= 32× 4864 - 45× 3458 ①
所以x = 32，y = -45

素数算数的基本定理

素数

定义

n是一个整数,且 n≠0,n≠±1，若n只有平凡因数（±1和±n）,则称整数n为素数，否则称为合数。

性质

1. 设p是一个素数，a,b为任意整数。

(1）若p∤a，则p与a互素
(2）若p|ab ，则p|a或 p|b

1. 任一不为1的非零正整数n 均可唯一地表示为有限个素数的幂的积，即：

其中p和α都是素数。上式称为n的标准分解式。

定理

1. 素数有无穷多个
2. 形如4k-1素数有无穷多个。
3. 设n是一个正整数。如果对于所有的素数p≤，都有p∤n ，则n是素数。

   利用第三点可以快速判断一个数是否为素数。

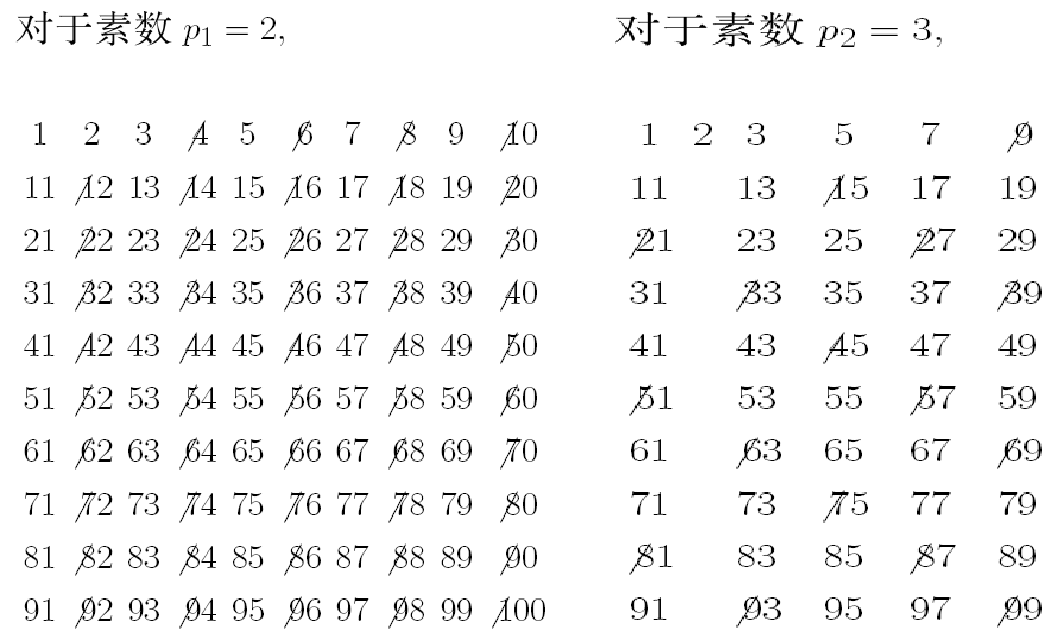
举个例子：求出100以内的所有素数。
由于小于=10的素数为2,3,5,7，所以只需要把这四个数可以整除的数全部去除即可

整数分解

整数分解问题指的是给定一个整数n，找到其素因子分解，即将n写成p1α1p2α2…pkαk的形式。
常用算法：

• 试除法
• Pollard rho 算法
• Pollard p-1算法
• 椭圆曲线算法
• 特殊数域筛法等

  特殊素数

  Mersenne 素数

  设n>1是一个正整数，若an -1是素数，则a = 2, n是为梅森数，梅森数为素数的时候，an -1为梅森素数。

  Fermat素数

  形如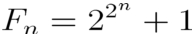的数称为Fermat数，当Fn是素数时，称为Fermat素数。
  如果2**n** + 1 是素数，那么n一定是2的方幂。

整数的表示

定义

如果b>2为整数，那么任意正整数a都可以唯一表示为: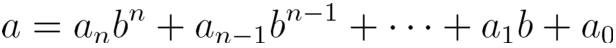

这种表示，称为a的基为b或者b进制的表示。
关于进制转换参见：
第一章：开关理论基础

b进制运算

遵循一个法则：满d进1，其余跟十进制相同。