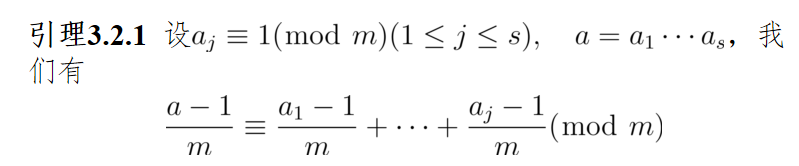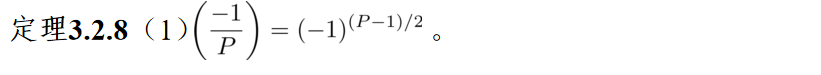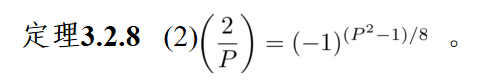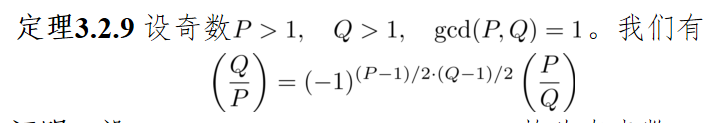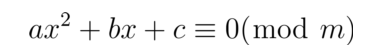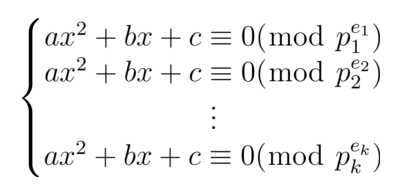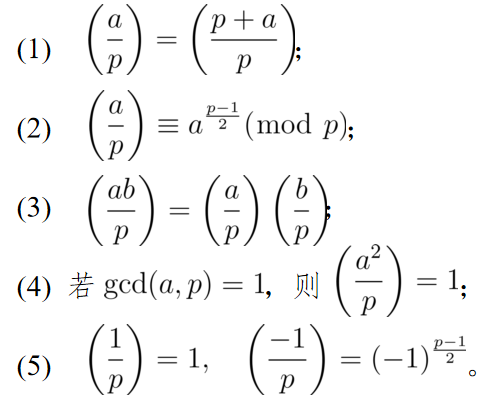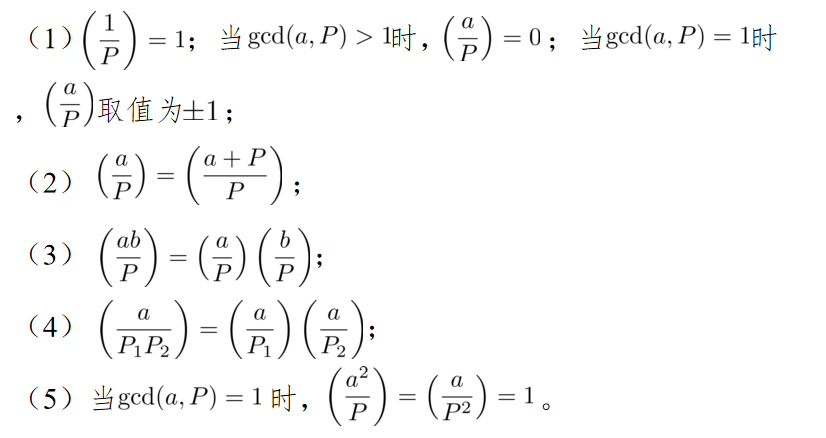同余方程和中国剩余定理
同余方程
什么是同余方程
同余方程的形式如下:
假设: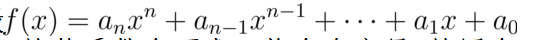
是一次数为**n**的整系数多项式,将含有变量**x**的同余式:
f(x) ≡ 0 (mod m)
就是一个同余方程,方程的解就是当f(c) ≡ 0 (mod m)时,c就是x 的一个解。
其中n就是f(x)的次数。
同余方程有解的充要条件
同余方程不一定有解的,如果同余方程**ax ≡ b(mod m)**有解,那么就有:
gcd(a,m) | b
解的数量就是:**gcd(a,m)**
注意:其实一般情况下同余方程的解是一个集合,数目是无穷多个,但是这里只需要求解在
0~m-1也就是小于m的正数解即可。
求解同余方程
求解步骤如下:
例如:求解9x ≡ 12(mod 15)
解答如下:
① 首先判断是否有解
根据上述的充要条件,可以计算出**gcd(9,15) = 3**,而3正好可以整除12,也就是3|12,所以可以得出同余方程有解,并且解的数量是**3个**。
② 所有的数除以计算出来的最大公因数
方程等价于**3x ≡ 4(mod 5)**。
同时两边同时乘以一个3模5的乘法逆元,也就是2,可得:6x ≡ 8(mod 5) => x ≡ 3(mod 5)
此时可以写出x的解集:x = 5k + 3,其中k为任意整数,在15以内的正整数有:{3,8,13}
所以这道题的解就是x=3,8,13
复杂的乘法逆元可以通过辗转相除法求解,参见
详细教学参见视频:
点击查看【bilibili】
中国剩余定理
定义
如果m1,m2,...,mk是两两互素的正整数,则同余方程组: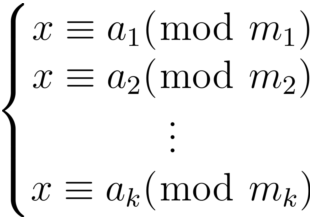
对模m = m1m2...mk有唯一解。设**M = m****1****m****2****...m****i-1****m****i+1****...m****k**,**M****i****'**为**M****i**对模整数**m**的逆元,方程组的解为: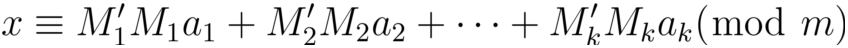
例题讲解
需要求解的同余方程如下: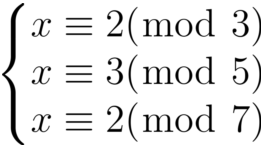
求解过程如下:
① 首先判断是否有解
模数分别是3/5/7,三个数两两互素,所以可以直接求解。
② 接着根据定义,求解**M**和**M'**即可M的求解:**M = m****1****m****2****...m****i-1****m****i+1****...m****k**
- m1 = 3,所以M1 = 5 * 7 = 35
- m2 = 5,所以M2 = 3 * 7 = 21
- m3 = 7,所以M3 = 3 * 5 = 15
M'的求解:**M****i****'**为**M****i**对模整数**m**的逆元
- m1 = 3,M1 = 35,所以M1’ = 2
- m2 = 5,M2 = 21,所以M2’ = 1
- m3 = 7,M3 = 15,所以M3’ = 1
③ 写出同余方程组的解:
a1 = 2 ,a2 = 3,a3 = 2
m = m1m2m3 = 3 5 7 = 105
x ≡ 2 35 2 + 1 21 3 + 1 15 2(mod 105)
x ≡ 23 (mod 105)
所以最终同余方程组的解就是**x ≡ 23 (mod 105)**
点击查看【bilibili】
定理
定理一:如果m1,m2,...,mk是两两互素的正整数,m = m1m2...mk,则同余方程: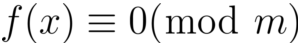
和同余方程组: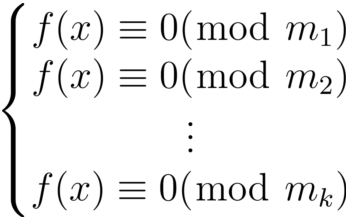
有相同的解。
这个定理可以在同余方程求解乘法逆元比较复杂的时候使用,例如下面这题:
23 和 140的乘法逆元求解需要用到辗转相除法,相对复杂,此时就可以转为同余方程组来求解。
注意,这里切记写出来的同余方程组的模数两两互素。
不互素的情况
前面的情况都是模数之间两两互素,如果有不互素的情况,例如:
处理方式如下:
根据上面所接触到的定理,可以把方程组的单个方程化为互素的方程组:
例如这里把10化为2和5,其余也是以此类推,接着再对这些方程组进行化简: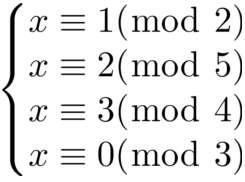
这里会返现模数里面还有2和4并不互素,由同余的定理:
x ≡ a (mod m) => x ≡ a(mod d) ,d|m
可得,由于2|4,所以模4的解一定是模2的解,所以又可以省略一个方程: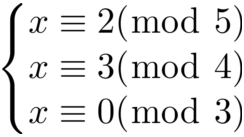
模重复平方算法
模重复平方算法用于解决**a****n****(mod m)**的计算,例如计算21000000(mod 77)。
运算的过程如下:
- 把
n转为二进制:n = n**020 + n**121 + … + n**k-1**2k-1 - 假设a = a,r = 1,遍历
ni的集合({n**0,n**1,…,n**k-1**})- 如果
i = 0,a不变;如果i ≠ 0, a = a2(mod m) (a2在模m下的余数) - 如果
ni = 0,r不变;如果ni = 1,r = r*a (mod m)
- 如果
- 遍历结束之后,r = an (mod m)
举个例子:计算21000000(mod 77)
① 首先根据欧拉定理进行化简:
φ(77) = φ(7) φ(11) = 6 10 = 60
由于gcd(2,77) = 1,所以260 ≡ 1 (mod 77),那么:21000000 = (260)16666 240 ≡ 240 (mod 77)
② 采用模重复平方算法:
由于40 = 1 23 + 1 25,所以可知:n**0,n1,n2,n4 = 0 , n3,n5**=1,假设a0 = a = 2,r = 1*
对n进行遍历可得:
- 由n0 = 0,i = 0,得:a0 = a = 2,r0 = r = 1
- 由n1 = 0,i = 1,得:a1 = a02(mod 77) = 4 ,r1 = r0 = 1
- 由n2 = 0,i = 2,得:a2 = a12(mod 77) = 16 ,r2 = r1 = 1
- 由n3 = 1,i = 3,得:a3 = a22(mod 77) = 25 ,r3 = r2 * a3 (mod 77)= 25
- 由n4 = 0,i = 4,得:a4 = a32(mod 77) = 9 ,r4 = r3= 25
- 由n5 = 1,i = 5,得:a5 = a42(mod 77) = 4 ,r5 = r4 * a5 (mod 77)= 23
所以综上,r5 = 23 = 240 (mod 77)
此题的解法二就是利用中国剩余定理的性质做的,这里放一下了解即可

二次同余方程和二次剩余
二次同余方程
二次同余
在了解方程之前,首先了解一下什么是二次同余(也叫二次剩余)。
当同余式满足:
x2 ≡ a (mod m) ,(a,m) = 1
此时a为模m下的二次同余(剩余),否则称a为模m的二次非剩余。
举个例子:求解模11的所有二次剩余和二次非剩余。
① 写出所以小于模11的正整数,依次求解平方后的余数:
| x | 1,10 | 2,9 | 3,8 | 4,7 | 5,6 |
|---|---|---|---|---|---|
| a ≡ x2(mod 11) | 1 | 4 | 9 | 5 | 3 |
② 所有求解出来的余数集合就是模11的所有二次剩余,所以
模11的二次剩余:1,3,4,5,9-
二次同余的定理
定理一:在
模p的一个既约剩余系中,恰有个
模 p的二次剩余,个
模 p的二次非剩余。
定理二:(欧拉判别法)设p为一个奇素数,gcd(a,p) = 1 。a是模p的二次剩余的充要条件是: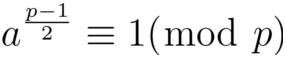
a是模p的二次非剩余的充要条件是: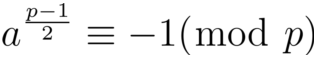
举个例子:判定8是不是17的二次剩余
这里就可以利用定理二,首先求解出(17 - 1)/2 = 8,88 ≡ 1(mod 17),所以是二次剩余。二次同余方程的定义
勒让德符号
定义
设
p是奇素数,a是整数,关于整变量a的函数:
称为模p的勒让德符号。性质
定理
定理一:(高斯引理),假设p为奇素数,a是整数,并且p不能整除a,再假设
1≤j≤p/2,那么如果:
tj ≡ ja(mod p), 0< tj < p
假设n为tj中大于p/2的数的个数,那么有:
定理二:设p是一个奇素数。符号[x]表示对x取整数部分- 当gcd(a,2p) = 1时,
,其中:
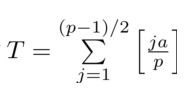
- (二次互反律)设p,q均为奇素数,p≠q,那么有
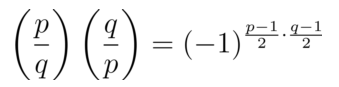
例题:计算
根据上面的二次互反律可得:
很容易根据勒让德符号的定义得出,(19/3) = (1/3),而1是模3的二次剩余,所以:
所以得出原式答案为-1。
判断同余方程是否有解
例如:判断同余方程x2 ≡ 7(mod 227)是否有解
判断的依据是**7**是否是**227**的二次剩余,如果是就代表有解,否则就是无解。
解题过程同上面那道例题,计算可得出(7/227) = 1,所以同余方程有解。
雅克比符号
定义
假设:奇数P > 1,P = p**1p2…pl,pi是素数**,定义: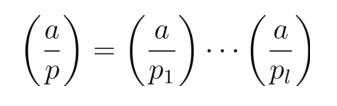
其中(a/pi)是a模pi勒让德符号,那么(a/p)是雅克比符号。
性质
定理