3.1 数据清洗

为什么要进行数据预处理

因为初始的数据可能会出现以下几种问题：
image.png
比较好理解，就不解释了。

数据预处理

数据预处理的步骤

  • 数据清洗
    • 填写缺失值，平滑噪声数据，识别或删除离群，并解决不一致问题
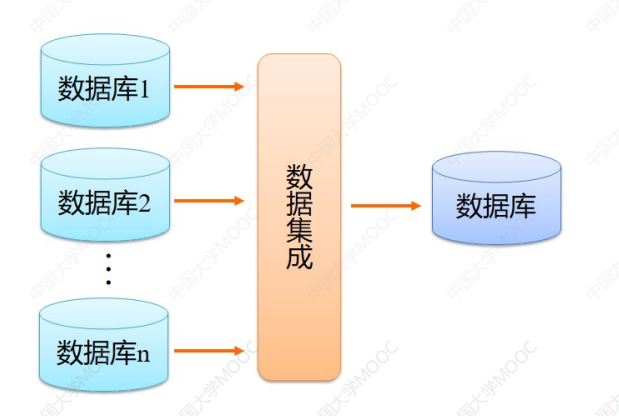
  • 数据集成
    • 整合多个数据库，多维数据集或文件
  • 数据缩减
    • 降维
    • Numerosity reduction（数据约减）
    • 数据压缩

  • 数据转换和数据离散化

    • 正常化（规范化）
    • 生成概念层次结构

      数据清洗

      我们获得的初始数据中可能存在如下几种情况：

  • “脏”数据:

    • 不完整的:缺少属性值，缺乏某些属性值，或只包含总数据
    • 例如，职业=“ ”(丢失的数据)
  • 含嘈杂的噪音，错误或离群
    • 例如，工资=“-10”(错误)
  • 不一致的代码或不符的名称
    • 年龄=“18”生日=“03/07/1997”
    • 曾经评级“1,2,3”，现在评级“A，B，C”

那我们清洗数据的时候就需要：

  • 填充或者删除脏数据
    • 在脏数据数目较小的时候可以直接删除
    • 脏数据数目较大就不可以，可以手动填写或者用属性的平均值自动填充
  • 去除或者修正杂音数据
    • 一般情况下都是直接删除
  • 更新不一致的名称
    • 计算推理
    • 全局替换，统一名称

      3.2 数据集成

      什么是数据集成

      将多个数据源的数据组合成一个连贯的数据源。
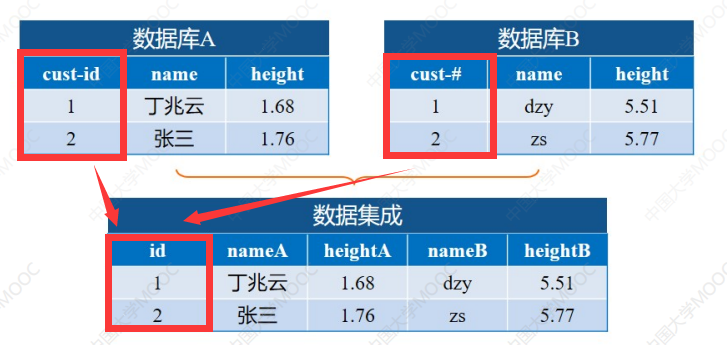
      image.png

      数据集成的要点

      模式集成

      比如两个数据库合并的时候，需要把意义相同的属性归并到一起：
      image.png

      这里的cust-id和cust-#很明显就是同一个意思，这里统一为id。

实体识别

上面的两个数据库中，名字的属性一个是中文名字，一个是中文名字首字母缩写，所以合并的时候需要进行一个统一：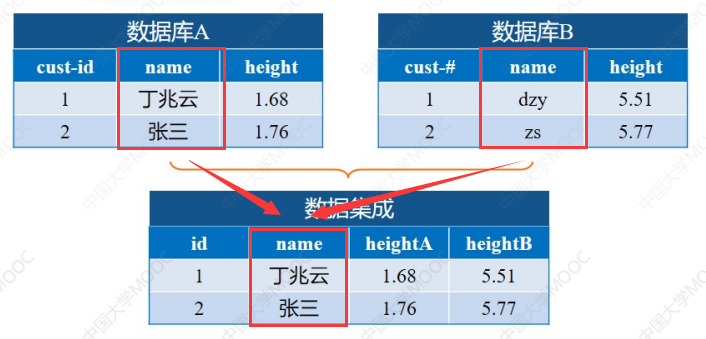
image.png

数据冲突和检测

发生的原因可能有两个：

  • 对于同一个真实世界的实体，来自不同源的属性值
  • 可能的原因:不同的表述，不同的尺度，例如，公制与英制单位

比如这里的两张表，一个单位肯定是米，另一个单位其实是英尺（课程里说的我也不知道是不是），所以集成在一个数据库的时候，需要统一单位。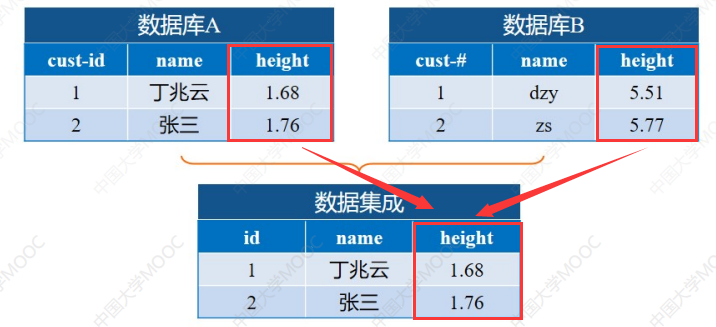
image.png
这里就是统一成“米”

冗余信息处理

整合多个数据库经常发生数据冗余

  • Object identification:相同的属性或对象可能有不同的名字在不同的数据库中
  • Derivable data:一个属性可能是“派生”的另一个表中的属性。

    第一个很好理解，类似于模式集成中的处理，第二个就好比有两个属性，一个是长度，一个是1/2的长度，显然只需要知道第一个就一定知道第二个属性，所以第二个属性就会被去除不做处理。

如果数据集比较大，特征数量比较多的情况下，怎么排查出冗余属性呢？
通过相关性分析和协方差分析可以检测到冗余的属性。

相关性分析——离散变量处理

相关性分析有如下公式（卡方检验）：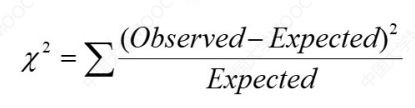
image.png
当X2的值越大，就表明越有可能两个变量（特征）是相关的。

注意这里的相关只是数据上的相关，并非实际因果关系上的相关，比如喜欢戴帽子的人和喜欢吃冰淇淋。

解释一下公式中的两个参数：

  • Expected：预期值
  • Observed：实际值

举个例子来解释：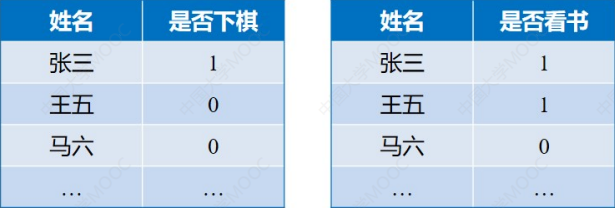
image.png
这里补充一下参数：

  • 1表示是，0表示否
  • 两个数据库数据总数相同，都为：1500
  • 下象棋的总人数：450
  • 看书的总人数：300

再加上其余的统计，我们可以绘制如下这张表：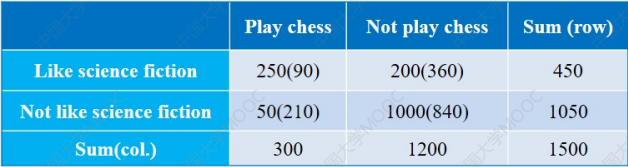
image.png

相信大家都看得懂英文，这里就类似于前面讲的二值属性邻近性度量。

重点关注这四个数据：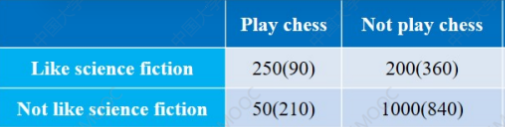
image.png
括号外面的是实际数据。

比如又下棋又看书的人是250

括号内部的是预期数据。

比如第一个括号里面的90，这个数据是由： 下棋的总人数（300）*看书的总人数（450）/数据总数（1500） = 90 其余的以此类推。

将上面表中的数据代入公式可得：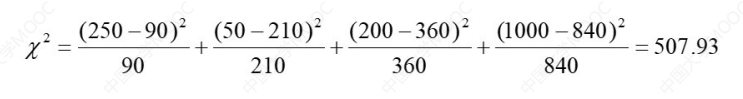
image.png
这就可以说明这两个数据相关度比较大了。

相关分析——连续变量的处理

连续变量的处理通常会涉及到一个相关系数的求解，我们称之为：皮尔逊相关系数。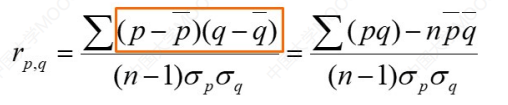
image.png
解释一下参数：

  • p和q是各自属性的具体值
  • p̄和q̄是各自属性的平均值
  • σp和σq是各自的标准差
  • n就是数据总数

我猜这里有人忘记标准差了，所以放一个标准差的计算公式：

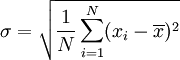
image.png

就不解释了，再看不懂去百度。

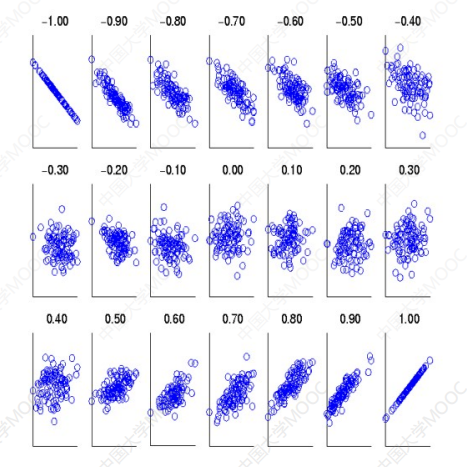
这个系数的含义如下：

  • 当r>0时，表示两变量正相关，r<0时，两变量为负相关。
  • 当r=1时，表示两变量为完全线性相关，即为函数关系。
  • 当r=0时，表示两变量间无线性相关关系。
  • 当0<r<1时，表示两变量存在一定程度的线性相关。且r越接近1，两变量间线性关系越密切;r越接近于0，表示两变量的线性相关越弱。
  • 一般可按三级划分:
    • r<0.4为低度线性相关;
    • 0.4≤r≤0.7为显著性相关;
    • 0.7<r<1为高度线性相关。

在散点图中的表示为：
image.png
与之相似的是协方差。

协方差

看一下协方差的公式：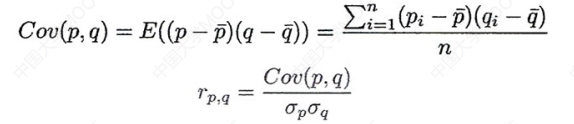
image.png
Cov还可以化简：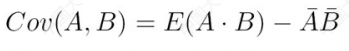
image.png

E是求解平均数

对比一下：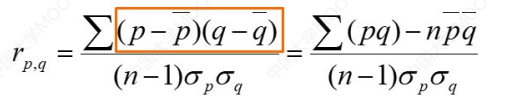
image.png
性质如下：

  • 正相关:cov(p,q)>0
  • 负相关:cov(p,q)<0
  • 独立性:cov(p,q)=0

接下来看个实例：
假设两只股票A和B具有在1个星期的以下值：


 第一天 第二天 第三天 第四天 第五天
股票A 2 3 5 4 6
** 5 8 10 11 14

问题:如果股票都受到同行业的趋势，他们的价格一起上升或下降?

首先分别计算两个股票的平均值：

  • E(A) = (2+3+5+4+6)/5 = 4
  • E(B) = (5+8+10+11+14)/5 = 9.6

由于只要看上升或者下降，就只需要计算Cov就可以了。
Cov(A,B) = ( 25 + 38 + 510 + 411 + 614)/4 - 49.6 = 4 >0

这里使用的是化简后的公式，是A和B对应属性值相乘求平均值 - 二者平均值相乘

所以很明显，价格一起上升。

3.3 数据规约

为什么要做数据规约

由于数据仓库可以存储TB级别的数据，因此在一个完整的数据集上运行时，复杂的数据分析可能需要一个很长的时间。
数据规约包含下面三个内容：

  • 降维
  • 降数据

  • 数据压缩

    降维

    什么是降维

    很简单，比如原始的数据集中有n个特征，降维就是通过把n个特征转化为m(m<n)个特征，来达到减少存储开销和计算时间的目的。

    为什么降维

  • 随着维数的增加，数据会变得越来越稀疏

    • 比如病例模型中，有些特征是和病因的关联不大，基本属于无效特征，所以需要降维减少这些无效特征。
  • 子空间的可能的组合将成倍增长（这个了解即可，后面会再讲相关概念）
    • 基于规则的分类方法，建立的规则将组合成倍增长
  • 类似神经网络的机器学习方法，主要需要学习各个特征的权值参数。特征越多，需要学习的参数越多，则模型越复杂
    • 机器学习训练集原则:模型越模型，需要更多的训练集来学习模型参数，否则模型将欠拟合。
    • 因此，如果数据集维度很高，而训练集数目很少，在使用复杂的机器学习模型的时候，首选先降维。
  • 维数太多，不便于可视化。

如何降维

一般采用的是PCA主成分分析法。
比如我们需要将下面的数据库进行降维：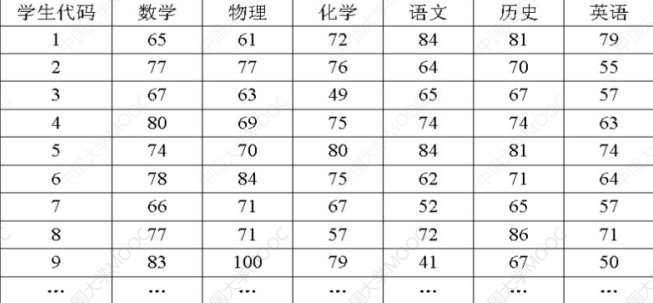
降维前 降维后
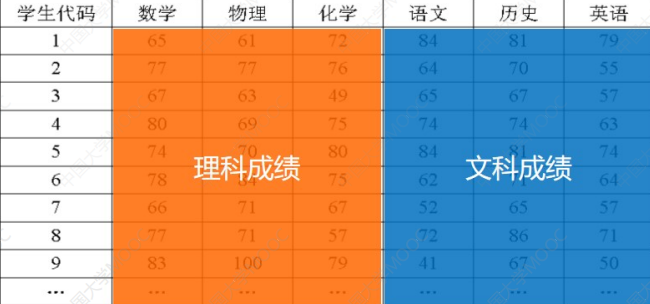
核心计算方法如下：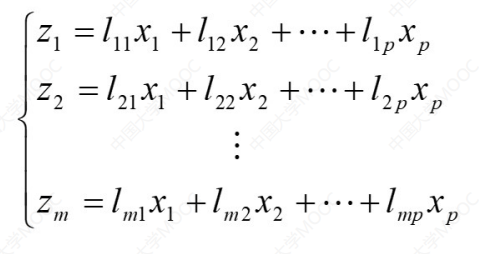
image.png
解释一下参数：

  • z是降维之后的新特征
  • x是降维前的特征
  • l是各个特征x对应的系数（视情况而定义）
  • 其中m一定是小于p的

    这里就是把前p个特征降维成为m个特征。

比如这里可以把理科成绩设置为z1，那么：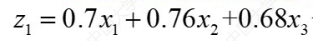
image.png
这里的x1，x2，x3就是数学，物理，化学。

这里的系数是通过算法得出的，详情可以参见下面这个视频。

点击查看【bilibili】

降数据

这个就很简单了，降数据的典型方法就是——抽样法：
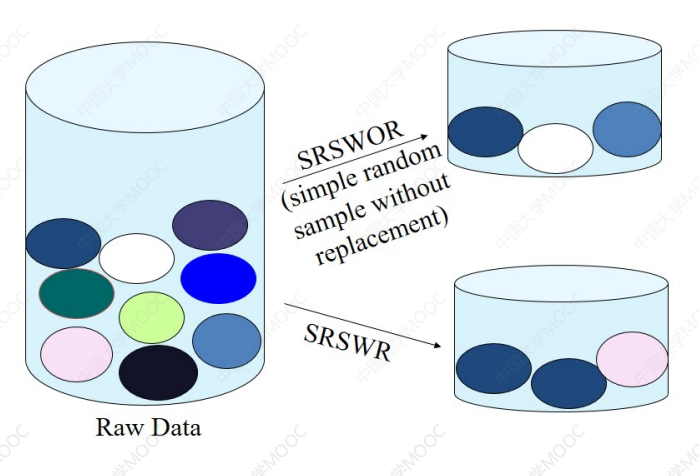
image.png

简单随机抽样

  • 相等的概率选择
  • 不放回抽样(Sampling without replacement)。
    • 一旦对象被选中，则将其删除

  • 有放回抽样(Sampling with replacement)

    • 选择对象不会被删除

      分层抽样

  • 每组抽相同个数

  • 用于偏斜数据

数据压缩

这个更简单了，就比如把图片的像素进行压缩，减少像素就减少了特征值。

3.4 数据转换

什么是数据转换

通过函数映射，指给定的属性值更换了一个新的表示方法，每个旧值与新的值可以被识别。
数据转换有两个方面：

  • 规范化
  • 离散化

规范化

为什么要规范化

假如我们需要研究学生的高考成绩，但是各个省份成绩的取值范围不一定相同，2020年江苏卷高考数学满分是200，全国卷数学满分是150，所以为了数据精准，我们需要把不同的范围规范到同一个范围当中。
规范化有三种常见方法：

  • 最小-最大规范化
  • Z-得分正常化
  • 小数定标规范化

最小-最大规范化

公式如下：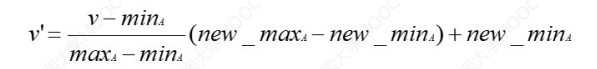
image.png
解释一下参数：

  • v：原先特征的值
  • v'：规范化之后特征的值
  • minA：原先特征A中的最小值
  • maxA：原先特征A中的最大值
  • new_minA：规范化后特征A中的最小值
  • new_maxA：规范化后特征A中的最大值

举个例子：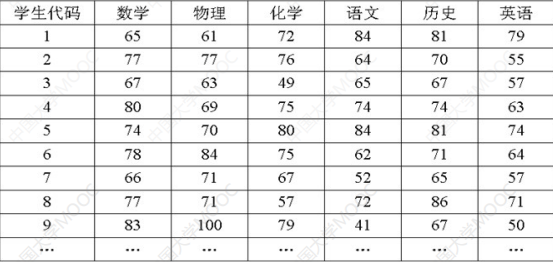
image.png
这里我们把分数都规范化，为了方便起见只取前面九个数据。
这里我们把分数规范化至0-1，所以new_minA=0那么new_maxA=1，以数学为例，minA=65，maxA=83。v就是65,77,67……

z-分数规范化

公式如下：
image.png
这个比较简单，就不讲解，具体讲一下什么时候用z-分数规范化：
在数据集是流式数据集的时候，也就是有源源不断的新数据进入数据集中，这个时候很难确定数据的最大值和最小值，所以通常用z-分数规范化。

小数定标

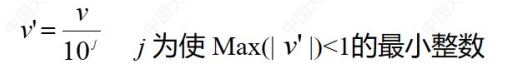
image.png
举个例子：假设一个特征的值的范围是300-10000，那么定标之后就是0.003-0.1。

最大的数定标之后刚好小于1即可。

离散化

为什么需要离散化

因为部分算法比较low，计算不了连续型，只能计算离散型，所以需要离散化
离散化有三种方法：

  • 等宽法
  • 等频法
  • 聚类

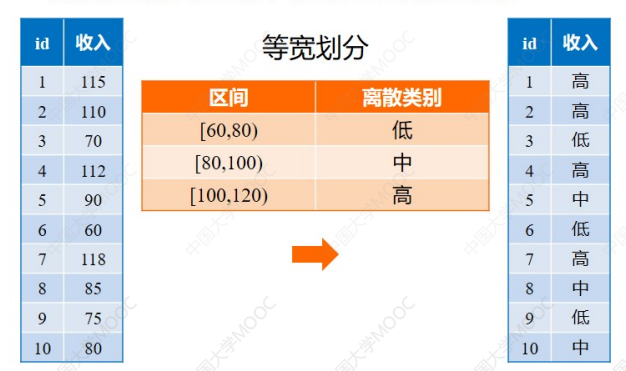
等宽法

根据属性的值域划分，使得每个区间的宽度相等：
image.png

等频法

根据取值出现的频数来划分，将属性的值域划分成个小区间,并且要求落在每个区间的样本数目相等：
image.png

这里一共十二个数据，需要分成三组，所以每组四个。

聚类

利用聚类将不同的类别划分成不同的离散类别。
比如原始的数据集如下：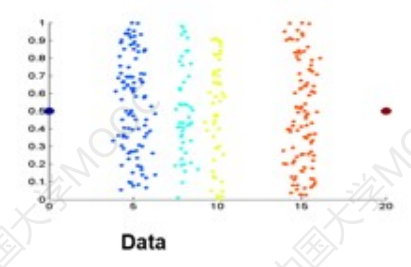
image.png
如果使用前两种方法：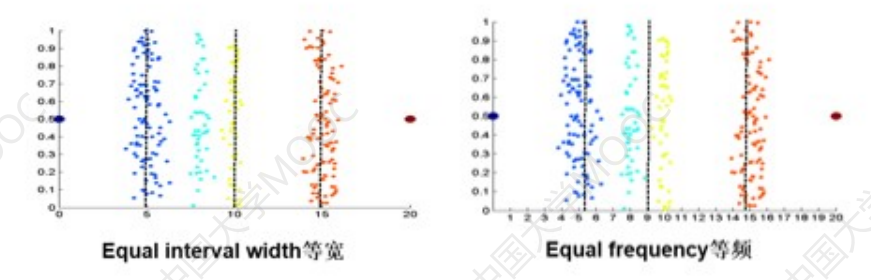
image.png
会发现分类的时候会把原本颜色离散的点分割开来，聚类的效果如下：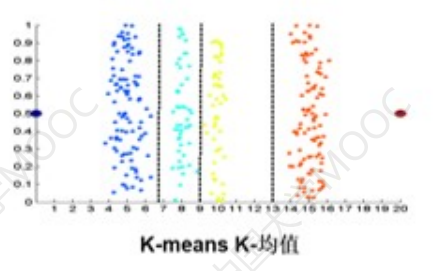
image.png

聚类是一个算法，这个算法后面会讲，这里只需要知道就可以。