数据结构与算法 - 第五章：树和二叉树 - 《计算机专业课笔记》

5.1 树的定义和基本术语
5.2 二叉树
5.3 二叉树的应用
5.4 树和森林
5.5 哈夫曼树（赫夫曼树）（重点）

5.1 树的定义和基本术语

树的递归定义

树是n(n>=0)个结点的有限集。它
（1）或者是一棵空树（n=0），空树中不包含任何结点
（2）或者是一棵非空树（n>0），此时有且仅有一个特定的称为根（root）的结点；当n>1时，其余结点可以分为m(m>0)个互不相交的有限集T1,T1,…,Tm，其中每一个本身又是一棵树，并且称为根的子树（subtree）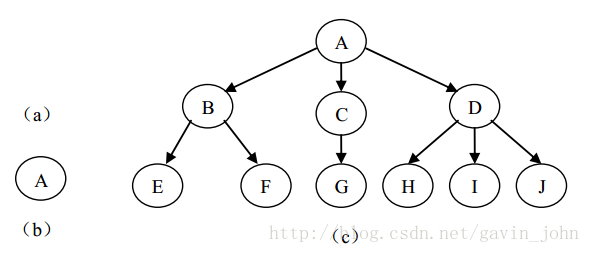
第五章：树和二叉树 - 图1

性质

树中的结点树等于树的边数加1，也等于所有结点的度数之和加1。
树中的结点数等于所有结点的度数加1
度为m的树中第i层上至多有m^(i-1)个结点(i>=1)
高度为h的m叉树至多有(m^h-1)/(m-1)个结点
具有n个结点的m叉树的最小高度为[logm(n*(m-1)+1)]

————————————————

版权声明：本文为CSDN博主「KLeonard」的原创文章，遵循CC 4.0 BY-SA版权协议原文链接：https://blog.csdn.net/gavin_john/article/details/72228937

5.2 二叉树

二叉树链表的表示方式

typedef struct BiNode{
    TElemType data;
    struct BiTNode * lchild,* rchild; //左右孩子指针，分别指向左右子树。
}BiNode,* BiTree;

遍历二叉树

代码实现：

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
typedef int TElemType;
typedef struct BiTNode{
     TElemType data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
void CreateBiTree(BiTree &T){
    TElemType ch;
    scanf("%d",&ch);
    if(ch == 0){
        T=NULL;
    }
    else {
        T = (BiTNode *)malloc(sizeof(BiTNode));
        T->data = ch;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    } 
};
void PreOrderTraverse(BiTree T) { 
//    printf("前序遍历的结果是：");
    if(T) 
    { 
        printf("%d",T->data);   
        PreOrderTraverse(T->lchild);   
        PreOrderTraverse(T->rchild);  
    } 
}
void InOrderTraverse(BiTree T){
//    printf("中序遍历的结果是："); 
    if(T) 
    { 
        InOrderTraverse(T->lchild); 
        printf("%d",T->data);  
        InOrderTraverse(T->rchild); 
    }  
}
void PostOrderTraverse(BiTree T) { 
//    printf("后序遍历的结果是：");
    if(T) 
    { 
        PostOrderTraverse(T->lchild); 
        PostOrderTraverse(T->rchild); 
        printf("%d",T->data); 
    } 
}
int main(){
    BiTree T;
    int n;
    printf("请创建一个二叉树：");
    CreateBiTree(T);
    while(n!=0){
        printf("前序遍历请输入1\n");
        printf("中序遍历请输入2\n");
        printf("后序遍历请输入3\n");
        printf("中止操作请输入0\n");
        scanf("%d",&n);
        if(n==1) {
            printf("前序遍历的结果是：");
            PreOrderTraverse(T);
            printf("\n");
        }
        if(n==2) {
            printf("中序遍历的结果是：");
            InOrderTraverse(T);
            printf("\n");
        } 
        if(n==3) {
            printf("中序遍历的结果是：");
            PostOrderTraverse(T);
            printf("\n");
        } 
        if(n==0) break;
    }
    return 0;
}

5.3 二叉树的应用

Status CountLeaf(BiTree T, int & count){
    if(T){
    if ((T->lchild==NULL)&&(T-> rchild==NULL)){
        count ++; return OK;
    }
    CountLeaf(T->lchild.count);
    //统计左子树中叶子结点个数
    CountLeaf(T-> rchild, count);
    //统计右子树中叶子结点个数
    }
    else return ERROR;
}

int Depth (BiTree T){
    if (!T) depthval = 0;
    else {
        depthLeft=Depth(T->lchild);
        depthRight=Depth(T->rchild);
        depthval = 1 + max(depthLeft,depthRight);
    }
    return depthval;
}

5.4 树和森林

5.4.1 树的存储结构-双亲表示法

树的顺序存储结构:用结构数组存放树的结点，每个结点含两个域:

数据域:存放结点本身信息
双亲域:指示本结点的双亲结点在数组中位置

树的双亲表存储描述:

#define MAX_TREE_SIZE 100
typedef struct PTNode {
    TElemtype data;
    int parent;
}PTNode;
typedef struct {
    PTNode nodes[MAX_ TREE_SIZE];
    int r,n;
}PTree;

优缺点：找双亲节点容易，找孩子节点难。

孩子链表的C语言描述

孩子结点结构:

typedef struct CTNode {
    int child;
    struct CTNode *next;
}*ChildPtr;

双亲结点结构

typedef struct {
    TElemType data;
    ChildPtr firstchild;//孩子链表头指针
}CTBox;

孩子链表结构:

typedef struct {
    CTBox nodes[MAX_TREE_SIZE];
    int n, r;//结点数和根结点的位置
}CTree;

优缺点：找孩子节点容易，找双亲节点难。为了解决找双亲节点难的问题，可以改进孩子链表。

改变双亲节点,双亲结点结构为:

typedef struct {
    int parent;
    TElemType data;
    ChildPtr firstchild;
}CTBox;

孩子兄弟表示法

树的二叉链表存储表示

typedef struct CSNode{
    ElemType data;
    struct CSNode *firstchild, *nextsibling;
}CSNode,*CSTree;

其中firstchild为该节点的第一个子节点，nextsibling是第一个兄弟节点。

优点：易于找到孩子节点
缺点：1.不宜查找双亲。2.破坏了树的层次。
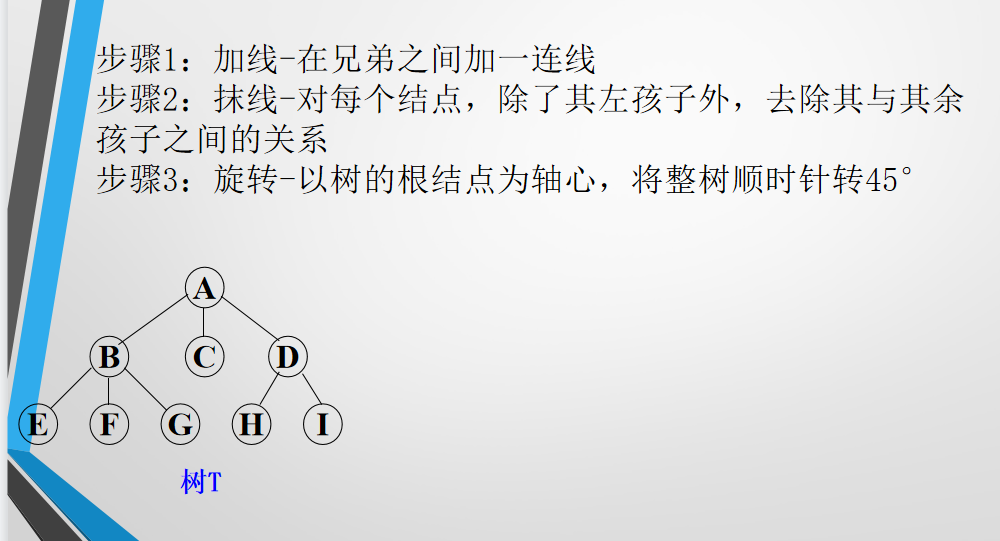
5.4.2 树转化成对应的二叉树

5.4.3 树的遍历
先根遍历:若树不空，先访问根结点，再依次先根遍历各棵子树
后根遍历:若树不空，先依次后根遍历各棵子树，再访问根结点

树的先根遍历相当于对应二叉树的先序遍历 树的后根遍历相当于对应二叉树的中序遍历

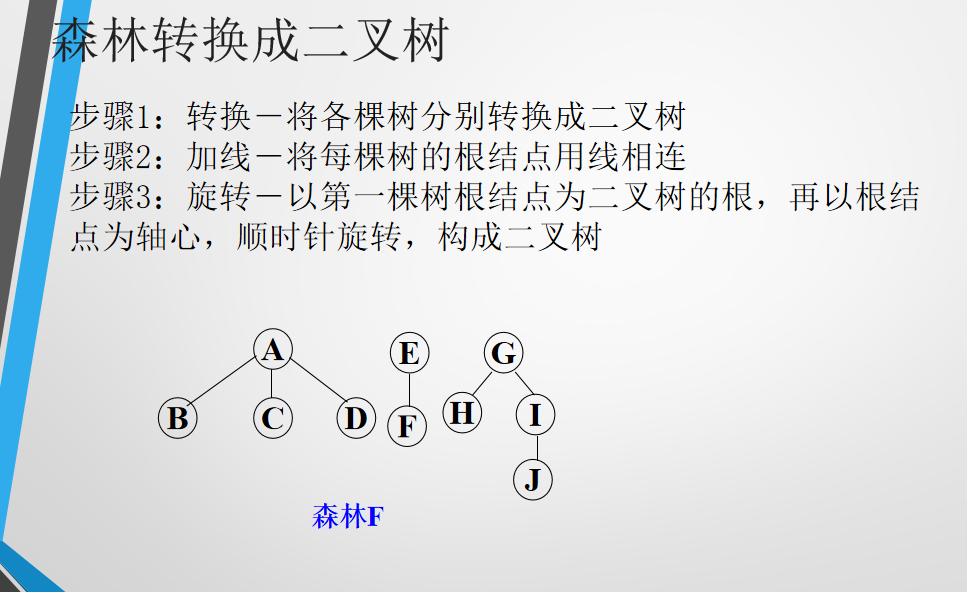
5.4.4 森林转化为二叉树（不重要）

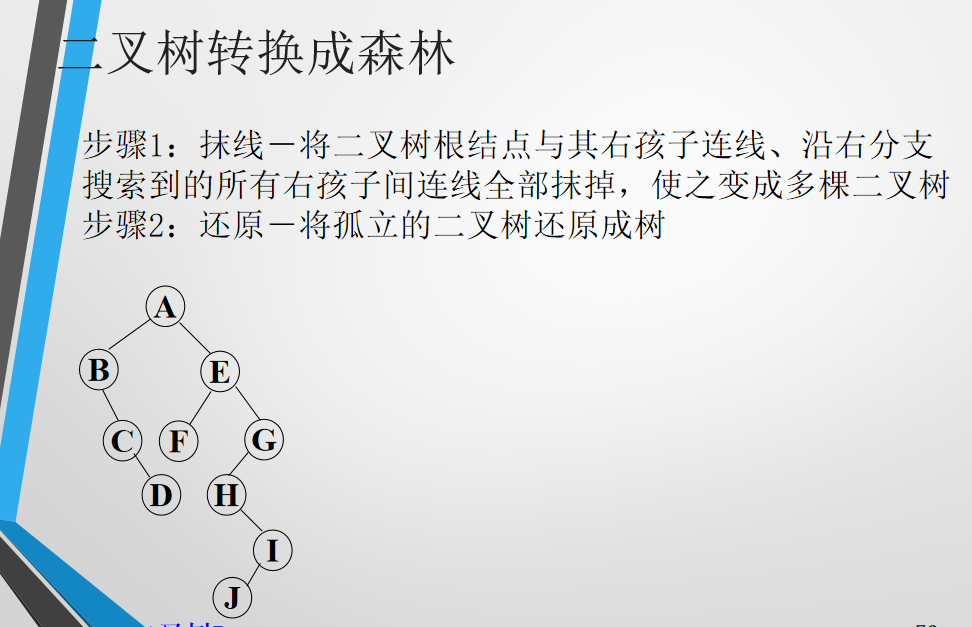
5.5 哈夫曼树（赫夫曼树）（重点）

前置定义：

两个结点间的路径:从树中一个结点到另一个结点之间的分支。
两个结点间的路径长度：路径上的分支数目。
树的路径长度：从树根到每个结点的路径长度之和。
权：一些有意义的实数
结点带权路径长度：从该结点到树根的路径长度与结点权的乘积
树的带权路径长度：树中所有叶子结点的带权路径长度之和

哈夫曼树（最优二叉树）：设n个权值{w1,w2,…wn}，构造一棵有n个叶子结点的二叉树，第i个叶子结点权值是wi，则其中带权路径长度最小的二叉树称为最优二叉树。
了解上述相关概念之后我们就可以直接开始构造最优二叉树（下面是重点中的重点）

方法：
步骤1：根据给定的n个权值{w1, w2, …, wn}，构造有n棵二叉树的森林F = {T1, T2, …, Tn}，Ti(1≤i≤n)中只有一个带权值wi的根结点，其左、右子树均为空。
步骤2：在F中选取两棵根结点权值最小和次小的二叉树作为左、右子树构造一棵新二叉树 Tk。Tk的根结点的权值为其左、右子树根结点的权值之和。

也就是说结点权值为1、2，组成行二叉树的节点权值为3。

步骤3：在F中删去这两棵二叉树（权值最小和次小的两个节点），把新的二叉树Tk加入F 。
步骤4：重复步骤2和步骤3, 直到F中仅剩下一棵二叉树为止，这棵二叉树就是最优二叉树。

说明：相同权值的叶子结点所构造的赫夫曼树不唯一，但带权路径长度之和相等。 在最优二叉树中没有度为1的结点，根据二叉树的性质3可知有n个叶子结点的二叉树有**n-1个非终端结点,共有2n-1个结点。

哈夫曼树的抽象存储结构

typedef struct{
    unsigned int weight;//权值
    unsigned int parent, lchild, rchild;//双亲结点，左、右孩子结点
}HTNode,*HuffmanTree;
typedef char ** HuffmanCode // 这里是一个指向char指针的指针

这里的unsigned指的是无符号，详细定义见

C语言中unsigned_bang152101的博客-CSDN博客_c语言unsigned
关于typedef char ** HuffmanCode
这里的HuffmanCode其实就是char**的别名，而char**是是一个指向char指针的指针类型，至于为什么要这么写，后面代码会再详细解释，这里理解是什么意思即可。

通常这种也叫作二级指针。

算法实现：

void HuffmanCoding ( HuffmanTree &HT, int *w,  int n )      
//这里传入了三个参数，一个是哈夫曼树HT，一个是权值w，一个是叶子节点的个数n
{  if (n<=1) return;
   //当叶子结点少于一个时候返回，因为本身就是一个哈夫曼树了。
   m=2*n-1;    
   //m用来表示结点的总个数
   HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode));
   //为哈夫曼树HT分配存储空间，m+1是因为数组下标都是从0开始的，而我们习惯从1开始表示结点，零位置空着不用，便于描述。
   for (p=HT, i=1; i<=n; ++i, ++p, ++w)  *p={*w,0,0,0}; 
   // 为叶子结点进行赋值，*w为该结点的权值，后面三个0分别为父节点，和左右子树。
   for ( ; i < =m; i++ ;++p)  *p={0,0,0,0};
   // 为非终端结点进行赋值，四个0分别表示结点的权值、父节点、左右子树
   for (i=n+1;i<=m;++i)
     {Select(HT,i-1,s1,s2);
     //挑选出权值最小的s1和权值次小的s2，这个算法在后面详细阐述
       HT[s1].parent=i; HT[s2].parent=i;
       //给权值最小和次小的结点的父结点进行赋值
       HT[i].lchild=s1; HT[i].rchild=s2; 
       //把这两个结点赋值给这个父结点的两个左右子树
       HT[i].weight=HT[s1].weight+HT[s2].weight;
       //父结点的权值是两个子树的权值之和
 }

完整代码：

#include<stdio.h> 
#include<stdlib.h>
#include<string.h>
#include<malloc.h>
# define MAX 1000
typedef struct{
    unsigned int weight;
    unsigned int parent,lchild,rchild;
}HTNode,*HuffmanTree;
typedef char **HuffmanCode;
void Select(HuffmanTree HT,int n,int &s1,int &s2){
    int i,change;
    int min1,min2;
    min1=MAX;
    min2=MAX;
    s1=0;
    s2=0;
    for(i=1;i<=n;i++)
    {
        if(HT[i].weight<min1&&HT[i].parent==0)
        {
            min2=min1; 
            s2=s1;
            min1=HT[i].weight;
            s1=i;
        }
        else if(HT[i].weight<min2&&HT[i].parent==0)
        {
            min2=HT[i].weight;
            s2=i;
        }
    }
    if(s1>s2)
    {
        change=s1;
        s1=s2;
        s2=change;
    }
}
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n){
    if(n<=1) return;
    int m,i,s1,s2,start,c,f;
    HuffmanTree p;
    char *cd;
    m =2*n-1;
    HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode));
    for(p=HT+1,i=1;i<=n;++i,++p,++w){
        *p={*w,0,0,0};
    }
    for(;i<=m;++i,++p){
        *p={0,0,0,0};
    }
    for(i=n+1;i<=m;++i){
        Select(HT,i-1,s1,s2);
        HT[s1].parent=i;HT[s2].parent=i;
        HT[i].lchild=s1;HT[i].rchild=s2;
        HT[i].weight=HT[s1].weight+HT[s2].weight;
    }
    HC=(HuffmanCode)malloc((n+1)*sizeof(char *));
    cd = (char *)malloc(n*sizeof(char));
    cd[n-1]='\0';
    for(i=1;i<=n;++i){
        start=n-1;
        for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent){
            if(HT[f].lchild==c) cd[--start]='0';
            else cd[--start]='1';
        }
        HC[i]=(char *)malloc((n-start)*sizeof(char));
        strcpy(HC[i],&cd[start]);
    }
    free(cd);
    printf("构建的赫夫曼树如下：\n");
    for(i=1;i<=m;i++)
    {
        printf("%d--%d--%d--%d\n",HT[i].weight,HT[i].parent,HT[i].lchild,HT[i].rchild);
    }
    for(i=1;i<=n;i++) printf("第%d个字符的编码是：%s\n",i,HC[i]);
}
int main()
{
    int *w;
    int n,i;
    HuffmanTree HT;
    HuffmanCode HC;
    printf("请输入叶子结点数目：");
    scanf("%d",&n);
    w=(int *)malloc(n*sizeof(int));
    printf("\n请依次输入%d个叶子结点的权值：",n);
    for(i=0;i<n;i++){
        scanf("%d",&w[i]);
    }
    HuffmanCoding(HT,HC,w,n);
    return 1;
}

更多关于赫夫曼树的讲解

哈夫曼树D_Double’s Journey-CSDN博客哈夫曼树

第五章： 树和二叉树