可算是到下一章了(>_>)
4.1 设计模式存在的问题
冗余存储:信息被重复存储,导致浪费大量存储空间。
更新异常:当重复信息的一个副本被修改,所有副本都必须进行同样的修改。因此当更新数据时,系统要付出很大的代价来维护数据库的完整性,否则会面临数据不一致的危险。
插入异常:只有当一些信息事先已经存放在数据库中时,另外一些信息才能存入数据库中。
删除异常:删除某些信息时可能丢失其它信息。
常见的就是这四大异常。
举个例子:
| studentNo | StudentName | courseNo | courseName | score |
|---|---|---|---|---|
| S0700001 | 李小勇 | C002 | 离散数学 | 82 |
| S0700001 | 李小勇 | C001 | 高等数学 | 98 |
| S0700001 | 李小勇 | C006 | 数据库系统原理 | 56 |
| S0700002 | 刘方晨 | C003 | 计算机原理 | 69 |
| S0700002 | 刘方晨 | C004 | C语言程序设计 | 87 |
| S0700002 | 刘方晨 | C005 | 数据结构 | 77 |
| S0700002 | 刘方晨 | C007 | 操作系统 | 90 |
| S0700003 | 王红敏 | C001 | 高等数学 | 46 |
| S0700003 | 王红敏 | C002 | 离散数学 | 38 |
| S0700003 | 王红敏 | C007 | 操作系统 | 50 |
冗余存储:学生姓名和课程名被重复存储多次;
例如:李小勇的名字被储存了三次,导致存储空间浪费。
更新异常:当修改某学生的姓名或某课程的课程名时,可能只修改了部分副本的信息,而其他副本未被修改到;
例如:刘方晨名字如果输入错误,需要修改,则需要修改四次,而如果其他表中含有刘方晨,但是其他表并没有修改,这就是更新异常。
插入异常:如果某学生没有选修课程,或某门课程未被任何学生选修时,则该学生或该课程信息不能存入数据库,因为主码值不能为空;
例如:新增了一门选修课名字为高等摸鱼学理论与实践,但是没有学生选修,而学生的学号在这个表作为主码不能为空,所以该课程不能插入这个表。
删除异常:当一学生的所有选修课程信息都被删除时,则该学生的信息将被丢失。对课程也是如此。
例如:删除
|S0700002 |刘方晨 |C003 |计算机原理 |69|,就会在表中丢失计算机原理的相关信息。
为了解释上述问题,可以对模式进行分解。
首先进行问题分析:SCE(studentNo, studentName, courseNo, courseName, score)模式产生问题的原因:
该模式中某些属性之间存在依赖关系
- studentNo→studentName(即学号决定姓名)
- courseNo→courseName(即课程编号决定课程名称)
- {studentNo, courseNo}→score(学生学号和课程号决定学生在该门课的成绩)
解决方法:
分解为三个关系模式 :
S(studentNo, studentName)C(courseNo, courseName)E(studentNo, courseNo, score)
模式分解存在的问题:(了解即可)
有损分解:
两个分解后的关系通过连接运算还原得到的信息与原来关系的信息不一致。
如果能够通过连接分解后所得到的较小关系完全还原被分解关系的所有实例,称之为无损分解(lossless decomposition),也称该分解具有无损连接特性。
依赖关系丢失:
依赖丢失就是存在依赖的丢失(这不废话嘛)。
如果被分解关系模式上的所有依赖关系都在分解得到的关系模式上保留,称该分解为依赖保持 (dependency preserving)分解。
4.2 规范化
4.2.1 几个基本概念
函数依赖
定义:函数依赖(functional dependency, 简称FD)是一种完整性约束,是现实世界事物属性之间的一种制约关系,它广泛地存在于现实世界之中。
简单的来讲就是 A->B,就是A能确定B,就说明AB存在函数依赖,B依赖于A。
几个函数依赖的类型
- 平凡函数依赖与非平凡函数依赖
- 完全函数依赖与部分函数依赖
- 传递函数依赖
定义1:在关系模式r(R)中,A⊆R,B⊆R。若A->B,但B不是A的子集,则称A->B是非平凡函数依赖。否则,若B⊆A, 则称A->B是平凡函数依赖。
对于任一关系模式,平凡函数依赖都是必然成立的,它不反映新的语义。所以我们一般都讨论非平凡函数依赖。
定义2:在关系模式r(R)中,A⊆R,B⊆R,且A->B。若对任意的C⊆A,C->B都不成立,则称A->B是完全函数依赖,简称完全依赖。
反之则称为部分函数依赖。
定义3:在关系模式r(R)中,A⊆R,B⊆R,B⊊A,C⊆R。若A->B,**B!->A(表示B不能确定A)**,B->C,则必存在函数依赖A->C,并称A->C是传递函数依赖,简称传递依赖。
注意:这里的条件
**B!->A(表示B不能确定A)**存在才成立传递函数依赖。
码
设K为R<U,F>中的属性或属性组合。若K->U为完全函数依赖,则K称为R的侯选码
这里的R表示关系集合,U表示所有的属性,F表示函数依赖关系的集合。K为U中的一个属性。 简单来讲就是:某一个属性或者多个属性的组合能函数确定所有属性的叫做候选码。 若候选码多于一个,则选定其中的一个做为主码。
主属性:包含在候选码中的属性。
非主属性:不包含在候选码中的属性。
4.2.2 范式(重点)
一定要把上面几个概念搞清楚再继续往后学习。
范式的种类:
- 第一范式(1NF)
- 第二范式(2NF)
- 第三范式(3NF)
- BC范式(BCNF)
- 第四范式(4NF)
- 第五范式(5NF)
重点是前四个范式,后面两个我也不会讲。 一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式的集合,这种过程就叫规范化
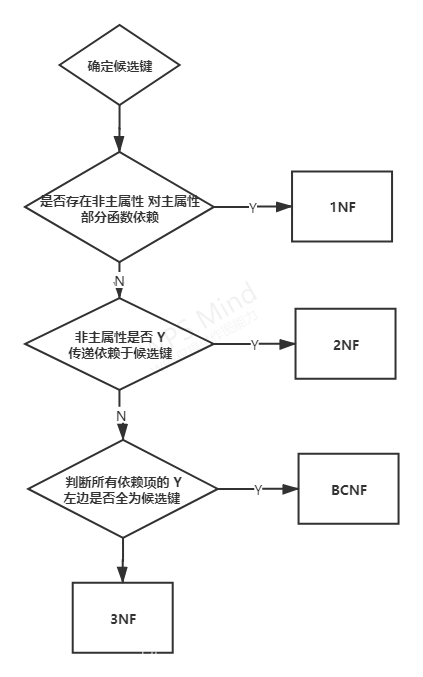
1NF(一范式)
定义: 如果一个关系模式R的所有属性都是不可分的基本数据项,则R∈1NF
简单的来讲就是表中不能再含有表 第一范式是对关系模式的最起码的要求。不满足第一范式的数据库模式不能称为关系数据库。 基本上后面遇到的范式最起码都是一范式。 基本上1NF都会存在上述四种异常。
例如:
| studentNo | StudentName | courseNo | courseName | score |
|---|---|---|---|---|
| S0700001 | 李小勇 | C002 | 离散数学 | 82 |
| S0700001 | 李小勇 | C001 | 高等数学 | 98 |
| S0700001 | 李小勇 | C006 | 数据库系统原理 | 56 |
| S0700002 | 刘方晨 | C003 | 计算机原理 | 69 |
| S0700002 | 刘方晨 | C004 | C语言程序设计 | 87 |
| S0700002 | 刘方晨 | C005 | 数据结构 | 77 |
| S0700002 | 刘方晨 | C007 | 操作系统 | 90 |
| S0700003 | 王红敏 | C001 | 高等数学 | 46 |
| S0700003 | 王红敏 | C002 | 离散数学 | 38 |
| S0700003 | 王红敏 | C007 | 操作系统 | 50 |
2NF(二范式)
定义: 若R∈1NF,且每一个非主属性完全函数依赖于码,则R∈2NF。
简单的来说就是在1NF的基础上消除了部分函数依赖。 就不存在属性,
A->B && AC->B。
例如:
| 学号 | 系名 | 系主任 |
|---|---|---|
| 1022211101 | 经济系 | 王强 |
| 1022211102 | 医学系 | 李思 |
| 1022511101 | 法律系 | 刘玲 |
这张表消除了部分函数依赖,但是
学号->系名,系名->系主任且系名!->学号,所以存在传递函数依赖。所以是一个二范式。
3NF(三范式)
定义:若R∈3NF,则每一个非主属性既不部分依赖于码也不传递依赖于码。
三范式就是在二范式的基础上在消除了传递函数依赖。
例如:
| 学号 | 系名 |
|---|---|
| 1022211101 | 经济系 |
| 1022211103 | 医学系 |
| 1022511101 | 法律系 |
或者
| 系名 | 系主任 | 工资 |
|---|---|---|
| 经济系 | 王强 | 5000 |
| 医学系 | 李思 | 6000 |
| 法律系 | 刘玲 | 7000 |
BCNF(BC范式)
定义:设F为模式R的依赖集,如果F中所有依赖X→A的左部(即X中)都包含了R一个候选关键字,则称R是Boyce—Codd范式,简记:BCNF。
(1)是BCNF的模式也必定是3NF,反之不一定。 (2)二元关系模式必定是BCNF (3)都是主属性的模式并非一定是BCNF。 (4)简单来讲就是在三范式的基础上,保证函数依赖左边的属性都是候选码
1NF↓ 消除非主属性对码的部分函数依赖消除决定属性 2NF集非码的非平 ↓ 消除非主属性对码的传递函数依赖凡函数依赖 3NF↓ 消除主属性对码的部分和传递函数依赖BCNF↓ 消除非平凡且非函数依赖的多值依赖4NF
4.3 Armstrong公理系统
下面几个记住即可:Armstrong公理系统: 设U为属性集总体,F是一组U上的函数依赖, X,Y,Z是属性集,对R(U,F) 有
- 自反律(reflexivity):若Y 包含于 X, 则X -> Y
- 增广律(augmentation):若X -> Y ,则XZ -> YZ
- 传递律(transitivity):若X -> Y,Y -> Z,则X -> Z
下面是推导:
(1)合并律(union rule)
若X -> Y,X -> Z,则X -> YZ
(2)分解律(decomposition rule)
若X -> Y Z 包含于 Y,则X -> Y,X -> Z
(3)伪传递律(pseudotransitivity rule)
若X -> Y,WY -> Z,则WX -> Z
逻辑蕴涵
定义:关系模式R(U,F),F是其函数依赖,X,Y是其属性子集,如果从F的函数依赖能够推出X->Y,则称F逻辑蕴涵X->Y,记作F├ X->Y。
如:
R(X, Y), F = {X->Y}能推出: X->X , X->XY
闭包
定义: 被F所逻辑蕴涵的函数依赖的全体所构成的集合,称作F的闭包,记作F+ = {X->Y | F├ X->Y}。(这里的+是在F的右上角)
例如:
R(X, Y), F = {X->Y}F+ = {X->空集, X->X, X->Y, X->XY,Y->空集, Y->YXY->空集,XY->X,XY->Y,XY->XY}
定义:如果X,Y是U的属性子集,X->Y能由Armstrong公理导出的所有Z的集合的并集就是X属性的闭包。
举个例子:
R< U, F >, U = (A, B, C, G, H, I), F = {A->B, A->C, CG->H, CG->I, B->H}求解AG属性的闭包
下面是求解过程:
- 首先AG能够确定自身,所以闭包里面包含了AG。
- 其次根据F直接的函数依赖有
A->B, A->C,可得闭包里面包含了ABCG。 - 在新的闭包里面继续根据函数依赖
CG->H, CG->I, B->H,可以确定HIG也是AG闭包的属性。 - 所以综上,AG 的闭包为
ABCGHI
注意一个是函数依赖的闭包,还有一个是属性的闭包 以上就是关于闭包的求解。
求解函数依赖的最小覆盖(重点)
首先看定义:
满足下列条件的函数依赖集F称为最小覆盖,记作Fmin:
(1)单属性化:F中任一函数依赖X -> A,A必是单属性(即A只能是X或者Y,不能是XY之类的组合属性)
(2)无冗余化:F中不存在这样的函数依赖X -> A,使得F与F-{X -> A}等价 (不包含冗余的函数依赖,这个很好理解)
(3)既约化:F中不存在这样的函数依赖X -> A,在X中有真子集Z,使得F与F - {X -> A} U {Z -> A}等价(简单来讲就是去除传递函数依赖)
来一个例子:
F = {A->BC,B->A,B->C, AB->C},求Fmin
- 首先逐个检查是否存在被确定属性不是单属性 的:
A->BC,将其拆分为A->B,A->C。 - 再检查是否存在冗余的函数依赖:
AB->C,所以将其去除。此时F = {A->B,B->A,A->C,B->C} - 接着检查是否存在传递函数依赖,从左往右检查会发现
A->B,A->C,B->C存在函数依赖,需要去除A->C。 - 所以最终
Fmin={A->B,B->A,B->C}
候选码的计算(重点)
首先要知道一个定义就是属性分类
- L类:只出现在函数依赖的左边的属性
- R类:只出现在函数依赖的右边的属性
- N类:在函数依赖的两边均未出现的属性
- LR类:出现在函数依赖的两边的属性
对候选码的判断:
- 如果X是L或N类属性,则X必为R的任一候选码的成员
- 如果X是R类属性,则X必不在任何候选码中
- 如果X是L和N类组成的属性组或者是L/N类其中一个,且X+包含了全部属性,则X是R的候选码
接下来介绍两种求算候选码的方法:
举个例子:
如设有关系模式R(U),其函数依赖集为F,其中:U={A,B,C,D,E},F={A->C,C->A,B->AC,D->AC}求R的候选码。
方法一:无脑计算闭包(慎用)
根据候选码的定义:设K为R<U,F>中的属性或属性组合。若K->U为完全函数依赖,则K称为R的侯选码
就是说有一个属性或者属性组K,K的闭包为所有属性的全集,那么K就是候选码。
所以我们就得到了一个暴力计算法:少到多把所有属性或者属性组的闭包求解出来,直到找到候选码为止
下面来求解
A+=ACC+=ACB+=ABCD+=ACDE+=EAB+=ABCAC+=ACAD+=ADC.....
最后可以求出候选码为:BDE
上述方法在属性比较少的时候可以用用,一般三四个就可以,五个及以上就用下面的方法。
方法二:快捷方法求候选码
首先根据候选码的判断:如果X是L或N类属性,则X必为R的任一候选码的成员。找出所有L和N类的属性(这边的属性是单属性,不是属性组)
不难得出就是:B D E
接下来对B D E求解闭包,根据候选码的判断可以依次增加属性求解闭包
B+=ABC,
(BD)+=ABCD,
(BDE)+=ABCDE,
发现有且仅有BDE就是属性的全集,所以直接得出BDE就是候选码,而且是唯一候选码。
如果把例题中关系模式R(U)中的属性E去掉,那么再求R的候选码的话可以根据得出
BD为R的唯一候选码。根据候选码的第一个判断,候选码一定包含了L或者N类,所以候选码必须有
BDE,如果BDE的闭包还不是U,那就逐步添加剩下的属性求解闭包。
为了方便讲解,这边再举一个例子:
R(ABCDEG)F={D->G,CD->E,E->D,A->B}
找出R类和N类可以得出:A C必然是候选码里面的属性。
求解AC闭包可得:AC+=ABC,发现并不等于U=ABCDEG
接下来添加的属性从U-AC+里面寻找,也就是从{D,E,G}中增加属性求闭包。
因为AC已经能够确定ABC了,所以不需要添加B就可以找到B。 (ACD)+={A,C,D,B,G,E} (ACE)+={A,C,E,B,D,G} (ACG)+={A,C,G,B} 这里不难看出已经找到了候选码,就是
ACD和ACE,所以本题答案就是ACD和ACE
候选码的求解基本方法集合shiter编写程序的艺术-CSDN博客求候选码
4.3+ 判断范式(重点)
现在要根据前三个小结的内容来学会怎么判断范式。
接下来是我的方法(有不对的请联系我纠正,有更好理解的欢迎补充)
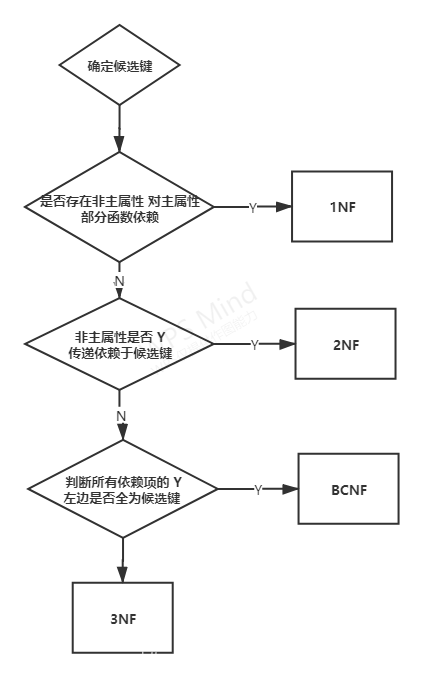
步骤:
- 首先求解关系中函数依赖的最小覆盖(去除多余的函数依赖,便于判断)。
- 接着判断关系中的候选码。
- 从1NF开始根据下面这张图往更高级别判断。
还是从例子开始看:
因为重点在于判断,所以这里我就把所有的函数依赖都已经写成最小覆盖,候选码也直接给出,读者可以自行求解一遍候选码。
R=(A,B,C),F={A→B,B→A,C→A}候选码:C
判断:
- 不包含表中表,所以肯定是1NF。
- 函数依赖的左边都是单属性,不存在部分函数依赖,所以肯定是一个2NF。
- 由
C->A,A->B可得出C->B,并且A!->C(这一点很重要),所以是存在传递函数依赖,所以不是3NF,只是一个2NF。
R=(A,B,C),F={A→B,A->C,C→A}候选码:A、C
判断:
- 不包含表中表,所以肯定是1NF。
- 函数依赖的左边都是单属性,不存在部分函数依赖,所以肯定是一个2NF。
- 由
C->A,A->B可得出C->B,但是A->C(这一点很重要),所以是不存在传递函数依赖,所以是3NF。 - 函数依赖的左边是
A、C,都是候选码,所以这是一个BCNF。
4.4 关系模式的分解
三种模式分解等价的定义
⒈ 分解具有无损连接性(保证分解后信息不丢失)⒉ 分解要保持函数依赖(减少各种异常情况)⒊ 分解既要保持函数依赖,又要具有无损连接性
满足上述三点,可以保证分解后的函数和原函数相等 。
模式分解的定义:把低一级的关系模式分解为若干个高一级的关系模式
一般情况下都是分解成三范式或者BC范式 把低一级的关系模式分解为若干个高一级的关系模式的方法不是唯一的 只有能够保证分解后的关系模式与原关系模式等价,分解方法才有意义
无损分解
关系模式R(U)的分解p={R1,R2},则p是一个无损连接分解的充要条件是 R1∩R2->(R1-R2)
简单来讲无损分解就是分解之后的模式通过等值连接可以恢复到原来的模式,那这个分解就是无损分解。
举个例子:
R=ABC, F={A -> B},p1={R1(AB), R2(AC)}R1∩R2 = A, R1-R2 = B由A -> B ,得到p1是无损连接分解P2={R1(AB), R2(BC)}R1∩R2 = B, R1-R2 = A, R2-R1 = CB->A, B->C均不成立,所以P2不是无损连接分解
这里只要会判断是不是无损分解就可以,因为我也不会怎么做到无损分解。
三范式分解
保持函数依赖的三范式分解
保持函数依赖通俗的来讲就是:如果F上的每一个函数依赖都在其分解后的某一个关系上成立,则这个分解是保持依赖的(这是一个充分条件)
算法描述
假设:关系模式R<U,F>,其中U属性集,F为属性集上的函数依赖,将其分解成3NF并保持函数依赖算法如下:
- 求F最小依赖集F’;
- 将既不在左部,又不在右部的属性,(就是N类属性)构成一个独立的一个关系模式K;
- 若有唯一依赖X->A,且XA=R,则分解只有一个R,结束;
- 将左部相同的所有函数依赖合并为一个新关系。每一个Xi->Ai,构成一个关系子模式Ri={XiAi}
- 关系模式K和所有的Ri就是保持函数依赖后的三范式分解
【例】关系模式R<U,F>,其中U={C,T,H,R,S,G},F={CS→G,C→T,TH→R,HR→C,HS→R},将其分解成3NF并保持函数依赖.
解:第一步: 求F的极小依赖集F’,F’={CS→G,C→T,TH→R,HR→C,HS→R}
第二步: 不存在既不在左部,又不在右部的属性;
第三步: 函数依赖左部相同的函数依赖合并,将合并后的每个函数依赖形成一个新的关系模式,
分解后ρ={R1(CSG),R2(CT),R3(THR),R4(HRC),R5(HSR)}
这里来对照一下最小函数依赖覆盖和分解后的范式一看就知道了。 F’={CS→G,C→T,TH→R,HR→C,HS→R} ρ={R1(CSG),R2(CT),R3(THR),R4(HRC),R5(HSR)} 假设U中增加了
AB两个属性,函数依赖F不变,那么只要再加一个R6(AB)就是分解后的模式集合。 下面是原题讲解
模式分解保持函数依赖3NF分解算法——数据库考试复习guoyp2126的博客-CSDN博客关系模式分解成3nf例题
既保证保持函数依赖又保证无损连接的三范式分解
直接上例题讲解:
【例】关系模型R<U,F>,U={A,B,C,D,E},F={A→BC,ABD→CE,E→D}
第一步:先将R转化3NF的保持函数依赖的分解,得出R1{A,B,C},R2{A,D,E},R3{E,D}。
第二步:求出F的候选码,得出候选码X为AD和AE。
第三步:将候选码单独组成关系得R4{A,D}和R5{A,E},然后与保持函数依赖后的分解取并集。得R1{A,B,C},R2{A,D,E},R3{E,D},R4{A,D},R5{A,E}。
第四步:观察新组成的分解模式中,是否存在包含关系,有则去掉被包含的。如R3{E,D},R4{A,D},R5{A,E}都包含于R2{A,D,E},则删去。
最终得到转化3NF的既有无损连接性又保持函数依赖的分解R1{A,B,C},R2{A,D,E}。
注意:这个分解的结果可能不唯一。 下面是原文章
数据库中转化为3NF的几个分解算法_Game_Zmh的博客-CSDN博客_3nf分解算法
BCNF分解
最后一个分解了
首先再来复习一遍BCNF的核心定义,在三范式的基础上保证函数依赖的左边都是主码
所以说只要保证分解后关系模式中函数依赖的左边都是主码,即可打到BCNF分解
算法
设r(R)为关系模式,r(R)不属于BCNF,若非平凡函数依赖A->B违反了BCNF的函数依赖
则将r(R)分解为r1(R1)和r2(R2),其中:
- R1=AB F1={A->B}
- R2=R-B F2为F上的投影
若r2(R2)不属于BCNF,则继续分解下去,直到所有结果模式都为BCNF。
关于F2是F上的投影,在原函数依赖中有且仅有R2属性的关系依赖的集合,的举个例子一看就懂 比如R={U(ABCD),F(A->B,C->D)} R1={U1(CD),F1(C->D)} R2={U2(AB),F2(A->B)}
下面照常举个例子:
[例]r(R)=r(A, B, C, D, G, H),F={A→BC, DG→H , D→A},r(R)是否属于BCNF范式?如果不是,则进行BCNF分解。
r(R)不属于BCNF(因为候选码为DG ,所以A→BC的决定属性A不是候选码)。按上述算法,r(R)可分解为
- r1(R1)=r1(A, B, C), F1={A→BC} —— A是候选码
- r2(R2)=r2(A, D, G, H),F2={DG→H , D→A}———DG是候选码
r2(R2)不属于BCNF(因为D→A的决定属性D不是候选码)。按上述算法,r2(R2)可分解为
- r21(R21)=r21(D, A), F21={D→A} —— D是候选码
- r22(R22)=r22(D, G, H), F22={DG→H} —— DG是候选码
最后, r1(A,B,C)、r21(D,A)和r22(D,G,H) 都属于BCNF。
所以BCNF分解之后就是 r1(A,B,C)、r21(D,A)和r22(D,G,H)
前前后后写了五个小时才把第四章笔记写完的,人麻了。