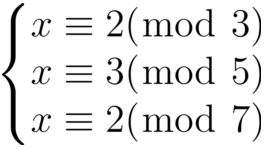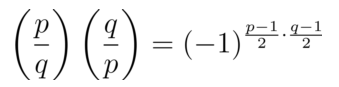期末复习题

整除

辗转相除法及其扩展算法

辗转相除法

题目：求解4864 和 3458 的最大公因数。

解答：利用的核心性质是：若a = bq+c ，q是一个整数，则有(a,b)=(b,c)

简单来说就是不断用b和b|a的余数r做带余除法。

4864 = 1 × 3458＋1406, q1 = 1,r1= 1406
3458 = 2 × 1406＋ 646， q2= 2,r2= 646
1406 = 2 × 646+114, q3 = 2,r3 = 114
646 = 5 × 114＋76, q4 = 5,r4 = 76
114 = 1 × 76＋38， q5 = 1,r5= 38
76 = 2 × 38 q6= 2,r6= 0
所以，最大公因数为：**38**

扩展算法

题目：求整数 x，y，使（4864，3458）=4864x+3458y

解答：
首先还是利用欧几里得算法求解最大公因数：
① 4864 = 1 × 3458＋1406, q1 = 1,r1= 1406
② 3458 = 2 × 1406＋ 646， q2= 2,r2= 646
③ 1406 = 2 × 646+114, q3 = 2,r3 = 114
④ 646 = 5 × 114＋76, q4 = 5,r4 = 76
⑤ 114 = 1 × 76＋38， q5 = 1,r5= 38
⑥ 76 = 2 × 38 q6= 2,r6= 0
易得，最大公因数为38
接下来依次从后往前反向表达最大公因数（从倒数第二个开始）：
38 = 114 - 76 ⑤
= 114 -(646-5×114) ④
= 646 +6 ×(1406 - 2×646) ③
= 6 ×1406 - 13×(3458-2 × 1406) - 13× 3458＋32× (4864 - 3458) ②
= 32× 4864 - 45× 3458 ①
所以x = 32，y = -45

证明题

题目：设(a, b)=1。证明：(d, ab)=(d, a)(d, b)

证明：

同余

大数据求模

题目：计算3801（mod 10）

解答:
采用以下性质：
若a1 ≡ a2 (mod m), b1 ≡ b2 (mod m)，则a1b1≡ a2b2(mod m)
这里的思路就是凑出余数为1的数，比如这里**3****4****(mod 10) = 1**。
可得**3****4 ****≡ 1 (mod 10) = 1**，根据以上性质，可得**（3****4****）200 ≡ 1200 (mod 10) = 1**

两边都是乘以自己。

那么原题可得：**（3****4****）200 + 1 ≡ 1200 * 3(mod 10) = 3**

求解欧拉函数

欧拉函数的定义

与m互素的剩余类的个数称为欧拉函数,记为φ(m)。
很显然，φ(m)的值就是一个完全剩余系里面与m互素的数的个数。

欧拉函数的性质

1. 设m,n是两个互素的整数，则φ(mn)= φ(m)φ(n)
2. 对于任意一个素数p，φ(p) = p-1
3. 
   

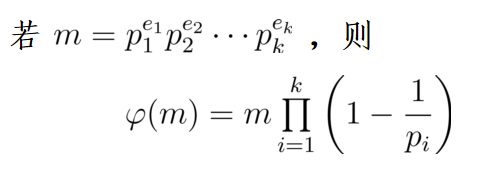
其中p为素数。

例题

题目：计算11，121，143和120的欧拉函数。

解答：
首先11是素数，有定理2可得，φ(11) = 11-1 = 10
121 = 11 11 = 112，所以根据定理3可得，φ(121) = 121 (1 - 1/11) = 110
143 = 13 11，可得13和11互素，所以φ(143) = φ(13) φ(11) = 12 10 = 120
120 = 23 3 5，根据定理三可得：φ(120) = 120 (1 - 1/2)(1 - 1/3)(1-1/5) = 32

注意分解的时候，每次保证p值为素数。

同余方程组

求解同余方程

求解步骤如下：

例如：求解9x ≡ 12(mod 15)

解答如下：
① 首先判断是否有解
根据上述的充要条件，可以计算出**gcd(9,15) = 3**，而3正好可以整除12，也就是3|12，所以可以得出同余方程有解，并且解的数量是**3个**。
② 所有的数除以计算出来的最大公因数
方程等价于**3x ≡ 4(mod 5)**。
同时两边同时乘以一个3模5的乘法逆元，也就是2，可得：6x ≡ 8(mod 5) => x ≡ 3(mod 5)
此时可以写出x的解集：x = 5k + 3，其中k为任意整数，在15以内的正整数有：{3,8,13}
所以这道题的解就是x=3,8,13

复杂的乘法逆元可以通过辗转相除法求解，参见

第二章： 同余

中国剩余定理

定义

如果m1,m2,...,mk是两两互素的正整数，则同余方程组：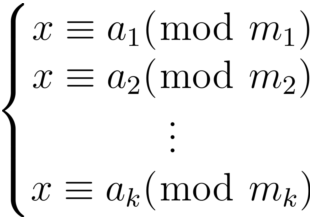

对模m = m1m2...mk有唯一解。设**M = m****1****m****2****...m****i-1****m****i+1****...m****k**,**M****i****'**为**M****i**对模整数**m**的逆元，方程组的解为：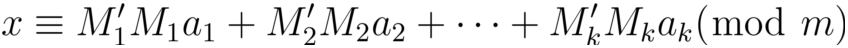

例题讲解

需要求解的同余方程如下：

求解过程如下：
① 首先判断是否有解
模数分别是3/5/7，三个数两两互素，所以可以直接求解。
② 接着根据定义，求解**M**和**M'**即可
M的求解：**M = m****1****m****2****...m****i-1****m****i+1****...m****k**

• m1 = 3，所以M1 = 5 * 7 = 35
• m2 = 5，所以M2 = 3 * 7 = 21
• m3 = 7，所以M3 = 3 * 5 = 15

M'的求解：**M****i****'**为**M****i**对模整数**m**的逆元

• m1 = 3，M1 = 35，所以M1’ = 2
• m2 = 5，M2 = 21，所以M2’ = 1
• m3 = 7，M3 = 15，所以M3’ = 1

③ 写出同余方程组的解：
a1 = 2 ,a2 = 3,a3 = 2
m = m1m2m3 = 3 5 7 = 105
x ≡ 2 35 2 + 1 21 3 + 1 15 2(mod 105)
x ≡ 23 (mod 105)
所以最终同余方程组的解就是**x ≡ 23 (mod 105)**
bilibili html5 player

同余方程转换同余方程组

定理

如果m1,m2,...,mk是两两互素的正整数，m = m1m2...mk，则同余方程：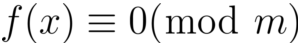

和同余方程组：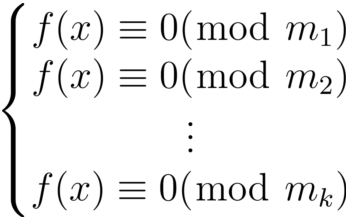

有相同的解。

例题

这个定理可以在同余方程求解乘法逆元比较复杂的时候使用，例如下面这题：

23 和 140的乘法逆元求解需要用到辗转相除法，相对复杂，此时就可以转为同余方程组来求解。

注意，这里切记写出来的同余方程组的模数两两互素。

不互素的情况

前面的情况都是模数之间两两互素，如果有不互素的情况，例如：

处理方式如下：
根据上面所接触到的定理，可以把方程组的单个方程化为互素的方程组：

例如这里把10化为2和5，其余也是以此类推，接着再对这些方程组进行化简：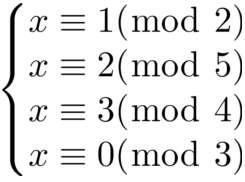

这里会返现模数里面还有2和4并不互素，由同余的定理：
x ≡ a (mod m) => x ≡ a(mod d) ,d|m
可得，由于2|4，所以模4的解一定是模2的解，所以又可以省略一个方程：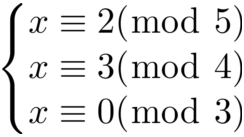

模重复平方算法

模重复平方算法用于解决**a****n****(mod m)**的计算，例如计算21000000(mod 77)。
运算的过程如下：

1. 把n转为二进制：n = n**020 + n**121 + … + n**k-1**2k-1
2. 假设a = a，r = 1，遍历ni的集合（{n**0,n**1,…,n**k-1**}）
   1. 如果i = 0，a不变；如果 i ≠ 0， a = a2(mod m) (a2在模m下的余数)
   2. 如果ni = 0，r不变；如果ni = 1，r = r*a (mod m)
3. 遍历结束之后，r = an (mod m)

举个例子：计算21000000(mod 77)

① 首先根据欧拉定理进行化简：
φ(77) = φ(7) φ(11) = 6 10 = 60
由于gcd(2,77) = 1，所以260 ≡ 1 (mod 77)，那么：21000000 = (260)16666 240 ≡ 240 (mod 77)
② 采用模重复平方算法：
由于40 = 1 23 + 1 25，所以可知：n**0,n1,n2,n4 = 0 , n3,n5**=1，假设a0 = a = 2,r = 1*
对n进行遍历可得：

1. 由n0 = 0,i = 0，得：a0 = a = 2，r0 = r = 1
2. 由n1 = 0,i = 1，得：a1 = a02(mod 77) = 4 ，r1 = r0 = 1
3. 由n2 = 0,i = 2，得：a2 = a12(mod 77) = 16 ，r2 = r1 = 1
4. 由n3 = 1,i = 3，得：a3 = a22(mod 77) = 25 ，r3 = r2 * a3 (mod 77)= 25
5. 由n4 = 0,i = 4，得：a4 = a32(mod 77) = 9 ，r4 = r3= 25
6. 由n5 = 1,i = 5，得：a5 = a42(mod 77) = 4 ，r5 = r4 * a5 (mod 77)= 23

所以综上，r5 = 23 = 240 (mod 77)

二次同余

二次同余的判定

定理一：在模p的一个既约剩余系中，恰有个模 p的二次剩余，个模 p的二次非剩余。
定理二：（欧拉判别法）设p为一个奇素数，gcd(a,p) = 1 。 a是模p的二次剩余的充要条件是：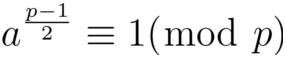

a是模p的二次非剩余的充要条件是：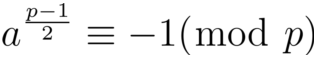

举个例子：判定8是不是17的二次剩余
这里就可以利用定理二，首先求解出(17 - 1)/2 = 8,88 ≡ 1(mod 17)，所以是二次剩余。

勒让德符号

定义

设p是奇素数，a是整数，关于整变量a的函数：

称为模p的勒让德符号。

二次互反律

（二次互反律）设p,q均为奇素数，p≠q，那么有

例题

题目：计算

根据上面的二次互反律可得：

很容易根据勒让德符号的定义得出，(19/3) = (1/3)，而1是模3的二次剩余，所以：

所以得出原式答案为-1。