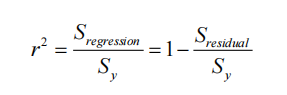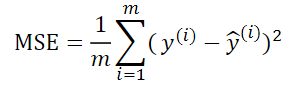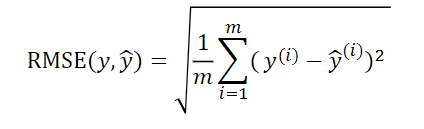线性回归

什么是线性回归

首先来普及一下监督学习的分类：

  • 回归
    • 主要是用于预测数值或者数值走向
  • 分类
    • 顾名思义就是划分种类，也是一种预测，预测种类。

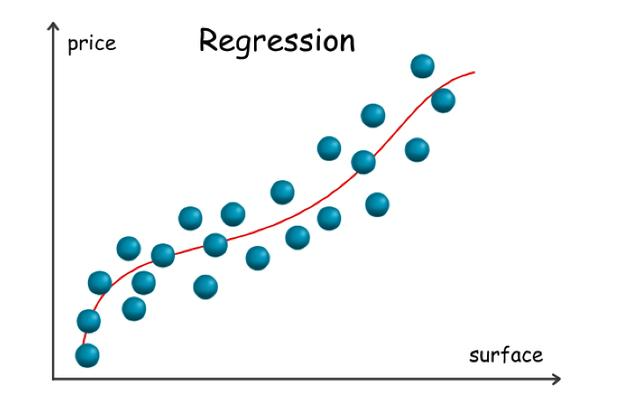
下面用两张图的来简单解释一下：
分类回归

图片源自：https://baijiahao.baidu.com/s?id=1667948615841074710&wfr=spider&for=pc

一看图就能明白：

  • 分类就是根据数据的不同种类，用一个函数分开多类数据
  • 回归就是根据数据的走向，用一个函数拟合数据的走向

那么这里的回归所求解出来的函数我们叫做目标函数，这个目标函数不一定能完全拟合所有的数据，所有肯定会有误差的存在，这个后面再讲。

符号约定

通常回归模型最基本的就是数据集：
T = {(x1,y1),(x2,y2),…..,(xn,yn)}
其中xi表示输入的变量，yi表示输出的应变量，T我们叫做训练集，一个(xi,yi)就代表了一个训练样本。

就分别代表在x轴和y轴上面的值，这个还是很好理解的。

还有以下需要申明的符号：

  • m：训练集中样本的数量
  • n：代表特征的数量
  • h：代表学习算法的解决方案或者函数（其实就是我们需要的目标函数）
  • h(x)：表示预测值

而上面的变量只有一个，所以我们一般称之为一元线性回归，但是实际上需要研究的变量不止一个，一个样本可能包含多个特征对结果有影响，也就是有多个变量，如下所示：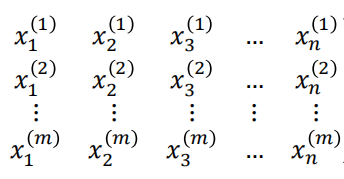
image.png
那么这里的下标**i**表示的是第i个特征，上标**j**表示第j个样本。
那么(x(j),y(j))表示的才是一个样本。
举个例子：
下面是建筑面积、总层数、楼层、实用面积关于房价的数据集：
image.png
红框中的数据可以表示为：
image.png

那么我们的预测函数h(x)是什么呢？
h(x) = w0 + w1x1 + w2x2 + … +wnxn
很明显就是一个关于所有特征的一个线性函数，其中：

  • w0：表示截距
  • wi：表示对应xi的回归系数

    我们由h(x)计算得出的值为预测值，数据集中给出的y为观测值（实际值），而观测值和预测值的差我们叫做残差。

代价函数和损失函数

首先我们要知道代价函数和损失函数都是基于目标函数h(x)的。我们知道我们给出的预测函数不一定是百分百准确的，肯定是多多少少存在误差的，这就衍生了这两个函数用来度量误差。
接下来看一下定义：

  • 损失函数：度量单样本预测的错误程度，损失函数值越小，模型就越好。
    • 0-1损失函数
    • 平方损失函数
    • 绝对损失函数
    • 对数损失函数等
  • 代价函数：度量全部样本集的平均误差。
    • 均方误差
    • 均方根误差
    • 平均绝对误差等。

      在有些情况这两个函数是没什么分别的，保证两个函数的最终值越小，得到的预测函数就越精准。

这两个函数最常用的计算方法就是平方损失函数和均方误差。

损失函数——平方损失函数

公式很简单：
image.png
简单来讲就是预测值减去实际值的平方。

代价函数——均方误差

公式也很简单：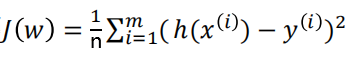
image.png
注意：这里的变量和损失函数是不一样的，损失函数变量是某一个样本的输入，而代价函数变量是所有的回归系数。
这里取平方有两个好处：

  • 由于残差可能是正的也可能是负的，所以可能存在不同样本之间的残差相互抵消，所以通过平方避免这种抵消。
  • 可以放大对结果影响较大的特征，缩小对结果影响较小的特征。

通过上述的了解，我们知道，如果想要求解出最精准的目标函数，就需要使得代价函数或者损失函数越小，那么这里有两个方法：

  • 最小二乘法
  • 梯度下降法

    两个方法

    一般情况下都是计算代价函数最小的时候，所以下面的方法都是针对代价函数。

    最小二乘法

    简单起见，假设特征变量只有一个，没有截距。也就是h(x) = wx
    我们把h(x(i)) = wxi代入均方误差公式当中，并拆开进行化简：
    image.png

    这里解释一下为什么是常数，因为所有的xi和yi都是数据集中给出的已知值。

所以不难看出，这个代价函数是一个一元二次函数，并且由于有平方的存在，所以a>0，也就是说这个二次函数是一个开口向上的函数，那么就可以得到：
image.png

也就是当红点到达最低点的时候，左侧的预测函数对数据的拟合度最高。

那么出现多个参数的时候：
image.png
核心的原理还是一样：寻找代价函数的最低点。

衍生到更高维度：
假设我们有的特征有n个，写成一个特征向量就是：
w=(w0,w1,w2,…,wn)
接下来写出样本的增广矩阵X，以及对应最后的结果Y：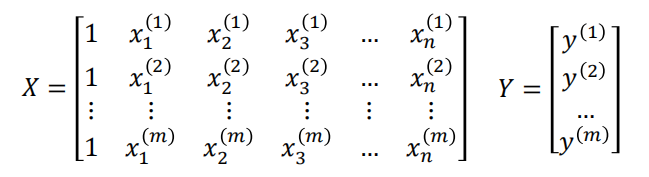
image.png
代价函数：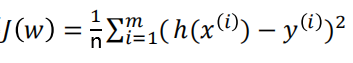
image.png
使用矩阵表示就是：
image.png
那么w的推导公式如下：
image.png
这里的推导有兴趣就自己看，这里只要记住最后的结果即可：
𝑤 = (𝑋T𝑋)-1 𝑋TY

本小节参考自：https://www.bilibili.com/video/BV1RL411T7mT/?spm_id_from=333.788 更多细节：https://zhuanlan.zhihu.com/p/38128785

梯度下降法

上面讲的是比较简单的情况，比如特征只有一个，且没有截距的时候，此时代价函数本质上是一个二次函数，那么可以通过高中的知识求出对称轴，从而直接获得最小的值。
然而实际的情况特征变量不止一个，这种情况就不能直接进行求解，这个时候就需要用到梯度下降。
那么什么是梯度下降？
还是举个最简单的例子：假设我们的代价函数就是上图所示的e = aw2 + bw + c
我们知道我们要需求的目标是代价函数的最低点，我们随机在代价函数上取一点，接下来我们就好比下山一样，需要一步一步向山脚走去。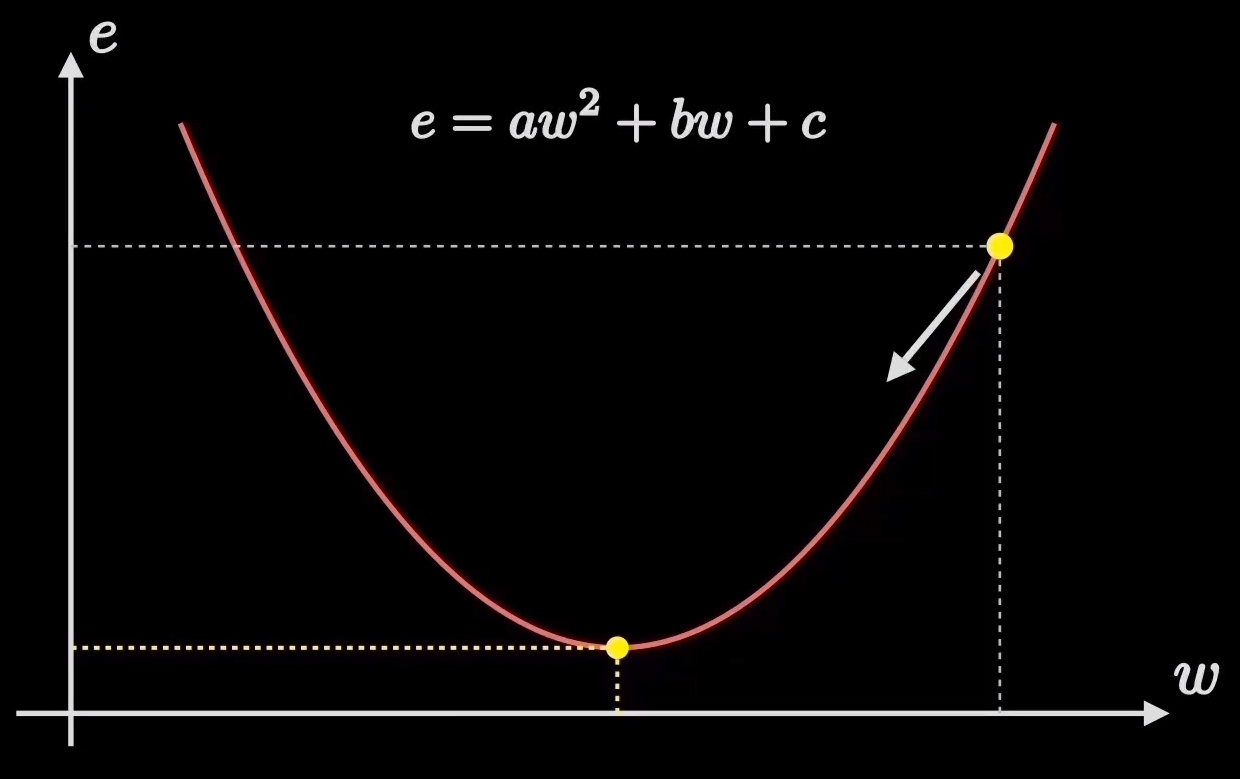
image.png
图中的黄点需要一次一次慢慢移动，一直到最低点，每次移动后两点之间的陡峭程度就是所谓的梯度。效果如下：
image.pngimage.pngimage.png
那么每次走多少就会影响最终找到最低点的速度，而这个我们称之为学习率𝛼。
学习率的大小会有如下影响：

  • 学习率过大：
    • 下降速度快
    • 难以在最低点收敛，大概率会在最低点附近左右横跳
  • 学习率过小：
    • 下降速度慢
    • 计算结果比较精准

所以一般情况下会设立适当的学习率。
每次下降之后都会更新**w**的值，那么：新w = 旧w - 斜率*学习率。

梯度下降又分为了三种形式：

  • 批量梯度下降（BGD）
    • 梯度下降的每一步中，都用到了所有的训练样本
  • 随机梯度下降（SGD）
    • 梯度下降的每一步中，用到一个样本，在每一次计算之后便更新参数 ，而不需要首先将所有的训练集求和
  • 小批量梯度下降（MBGD）
    • 梯度下降的每一步中，用到了一定批量的训练样本

详情可以参见：
梯度下降法的三种形式BGD、SGD以及MBGD - wyu123 - 博客园

本小节参考：https://www.bilibili.com/video/BV18P4y1j7uH/?spm_id_from=333.788

小结

  • 梯度下降：需要选择学习率𝛼，需要多次迭代，当特征数量𝑛大时也能较好适用，适用于各种类型的模型。
  • 最小二乘法：不需要选择学习率𝛼，一次计算得出，需要计算 𝑋𝑇𝑋 −1 ，如果特征数量𝑛较大则运算代价大因为矩阵逆的计算时间复杂度为𝑂(𝑛3)，通常来说当𝑛小于10000 时还是可以接受的，只适用于线性模型，不适合逻辑回归模型等其他模型。

正则化

为什么要正则化

在选模型的时候，需要选择的模型进度越高自然越好，但是如果选择的模型过于复杂，就可能会导致过于拟合，后续数据预测不一定都精准。
举个例子：
图片源自吴恩达机器学习视频课
上图中的拟合度从左到右精准度依次递增，复杂度也随之递增。

  • 第一张图：复杂度最小，精准度最低
  • 第二张图：复杂度适中，精准度适中
  • 第三张图：复杂度最高，精准度最高

一般情况下我们会采用第二个模型，保证了精准度的同时，也会放置模型过拟合。

只要记住，模型过于精准并不是一件好事，因为这个精准是针对训练数据的，测试数据并不一定能够符合这个模型，这种过于精准的模型我们称之过拟合。

所以为了防止模型过拟合，我们就引入了正则化项J(f)。
这个正则化项的作用就是用于约束模型的复杂程度。
这里有个新概念，我们称：

  • 模型的精准程度为经验风险
    • 经验风险越小，模型越精准
  • 模型的复杂程度为结构风险
    • 结构风险越小，模型越简单

那么我们综合要实现的线性回归函数就是：代价函数 + 正则化项，也就是我们需要同时优化经验风险和结构风险，才能得到一个最优的线性回归函数。
那么我们最终需要优化的函数就是：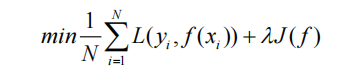
image.png
这里的λ是正则化的系数，也叫权重或者惩罚程度，这个值越大，说明惩罚程度越大，训练出来的模型越简单。
所以正则化的作用是选择风险与模型复杂度同时较小的模型。

L1正则化和L2正则化

这里我们需要知道我们所给的正则化项J(f)是一个关于w的函数，也就是模型中对应特征的系数。
最常见的两个正则化的方法就是L1正则化和L2正则化。

  • L1正则化可以使得模型变得更加平滑，并且使得模型稀疏化。
  • L2正则化可以使得模型变得更加平滑。

什么是平滑？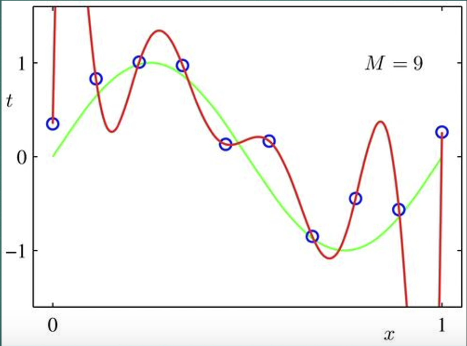
image.png
图中明显绿色的曲线更平滑，红色曲线更陡峭。

什么是稀疏化？
简单的来说，就是弱化甚至去除对预测结果影响较小的特征的系数w，从而达到降低复杂度的目的。

比如令y = w1x12 + w2x2 + w0中的w2=0，就降低了模型复杂度。

两个正则化项的计算公式如下：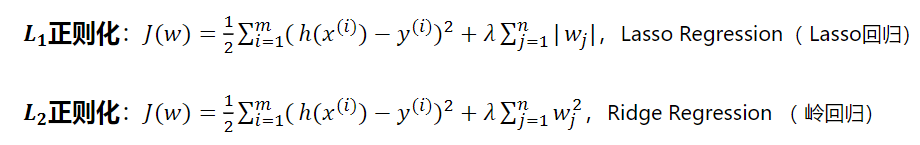
image.png
详细的原理以及推导过程参见：
点击查看【bilibili】
L1正则化与L2正则化

反正我是看不懂。

交叉检验

那么可以不可以不使用正则化来确定最终的模型呢，也是可以的，这里就可以使用交叉检验的方法。
如果给定的样本数据充足，进行模型选择的一种简单方法是随机地将数据集切分成三部分，分别为

  • 训练集
    • 训练接用来训练模型（简单来讲就是用于计算函数）
  • 验证集
    • 验证集用于模型的选择
  • 测试集
    • 用于最终对学习方法的评估

交叉检验又有一下三种方法：

简单交叉验证

首先随机第讲已给数据分为两部分，一部分作为训练集，另一部分作为测试集（例如，70%数据为训练
集，30%的数据为测试集）；然后用训练集在各种条件下（例如，不同的参数个数）训练模型，从而得到不同的模型；在测试集上评价各个模型的测试误差，选出测试误差最小的模型。

k折交叉验证

首先随机第将已给数据切分为K个互不相交、大小相同的子集；然后利用K-1个子集的数据选了模型，利用余下的子集测试模型；将这一过程对可能的K 种选择重复进行；最后选出 K 次评测中平均测试误差最小的模型。
image.png

留一交叉验证

K 折交叉验证的特殊情景是 S = N，称为留一交叉验证，往往在数据缺乏的情况下使用。这里 N 是给定数据集的容量。

模型的评价指标

假设我们已经通过计算得到了一个准确的模型（函数），那我们就需要一个指标，来衡量这个模型对数据预测的精准程度。
这个指标就是我们对模型的评价指标。

计算公式

一般我们使用r2来表示这个评价指标，它的计算公式如下：
image.png

参数解释

  • Sregression：回归平方和
  • Sy：总平方和
  • Sresidual：残差平方和

三个参数的计算公式如下：
image.png

这里的image.png表示的就是预测值。

还是很好理解的。
让
r2的取值范围是**[0,1]**，越接近0说明模型越不精准，越接近1说明模型越精准。

注意这里讲的模型精准是针对预测数据的精准。 上文中的经验风险相关的精准，是针对训练数据的精准。 模型对训练数据精准不代表对预测数据精准，这里注意辨别。

误差评价

MSE（均方误差）

image.png

RMSE（均方根误差）

image.png

MAE（平均绝对误差）

image.png
image.png

R^2误差

统计学里R^2表示什么_HOLD ON!的博客-CSDN博客_r值是什么

逻辑回归