4.1 数组的定义

在C语言中，一个二维数组类型可以定义为其分量类型为一维数组类型的一维数组类型。

  1. typedef Elemtype Array2[m][n];
  2. =>  typedef Elemtype Array1[n];
  3.     typedef Array1 Array2[m];

4.2数组的顺序表示和实现(重点）

特点:用一组地址连续的存储单元按照某种规则存放数组中的数据元素。

两种规则(顺序存储方式)∶

  • 以行序为主（低下标优先）—将数组元素按行排列，第i+1个行向量紧接在第i个行向量后。如:PASCAL、C。
  • 以列序为主（高下标优先）—将数组元素按列排列，第j+1个列向量紧接在第j个列向量后。如: FORTRAN。

用二维数组举个例子：

行序为主
a[0][0]
a[0][1]
a[0][2]
…
a[0][n-1]
a[1][0]
a[1][1]
a[1][2]
…
a[m-1][n-1]
列序为主
a[0][0]
a[1][0]
a[2][0]
…
a[n-1][0]
a[0][1]
a[1][1]
a[2][1]
…
a[m-1][n-1]

计算数组任一元素的地址

需要的三要素:

  1. 数组的起始地址（即基地址)
  2. 数组维数和各维的长度;
  3. 数组中每个元素所占的存储单元

[例1]已知二维数组Ab1*b2(即二维数组有b1行，b2列)，每个元素占L个存储单元，LOC(0,0)是第一个元素的起始地址，以行序为主存储，求LOC(i,j)。

  1. 行主序:LOC(i,j)= LOC(0,0)+(b2*i+j)*L
  2. 列主序:LOC(i,j)= LOC(0,0)+(b1*j+i)*L

解析：
二维数组存储结构如下：

  1. {
  2.     a[0][0],a[0][1],...a[0][b2-1]
  3.     a[1][0],a[1][1],...a[1][b2-1]
  4.     ...
  5.     a[b1-1][0],a[b1-1][1],...a[b1-1][b2-1]
  6. }

以行序列为例，在LOC(i,j)之前的行一共有i行(因为序列的索引是从0开始的)。 每一行都有b2个元素，所以一共有**b2*i个元素**。 在LOC(i,j)之前的列一共有j列 (因为序列的索引是从0开始的)。 所以这一列一共有j个元素。 每一个元素所占据的存储空间大小又是L。 所以地址为LOC(i,j)= LOC(0,0)+(b2*i+j)*L。


推广到n维数组(重点)

设各维长度分别为b1, b2, b3…，bn每个元素占L个存储单元，起始地址LOC(0,0,…,0)，求元素a[j1][j2]…[jn]的存储位置

  1. LOC(j1,j2,…jn )=LOC(0,0,....0)+
  2. (b2*b3*...*bn*j1 + b3*b4*...*bn*j2 + ……… + bn*jn-1 + jn )*L

现在我们把+后面的式子单独提出来讨论

  1. (b2*b3*...*bn*j1 + b3*b4*...*bn*j2 + ……… + bn*jn-1 + jn )*L

观察单独的每一项可以发现，**通式为；bi+1*bi+2*bi+3*....*bn*ji**,最后一项由于没有n+1项，所以是j**n。所有项再乘以一个L。
这里把L乘以到括号里面，再令`bi+1*bi+2*bi+3*….bnL = c**i,令cn = L。<br />不难发现一个规律：ci-1 = bi*ci`。
所以上述式子可以写成这个样子：

  1. LOC(j1,j2,…jn )=LOC(0,0,....0)+c1*j1+c2*j2+...+cn*jn;

这一块必须理解!


例题（重点）

数组M[1..10][-1..6][0..3]，起始地址是1000,每个元素占3个存储单元,数组元素个数是__，如采用行主序存储，那么M[2][4][2]的地址是__。

解：数组元素的个数：（10-1+1）（6-（-1）+1）（3-0+1）=320
LOC（M[2][4][2]）=1000+[48(2-1)+4(4+1)+2]3=1162

这道题会了就基本可以了。

4.3 数组结构体类型定义以及基本操作

  1. typedef struct {
  2.     ElemType *base  //存储空间基址
  3.     int dim         //数组维数
  4.     int *bounds     //数组维界基址
  5.     int *constants  //数组映象函数常量基址
  6. }Array

首先要了解的一个点是，我们可以定义n维数组，但是在计算机的存储中都是空间连续的一维数组。
现在来一个一个用人话解释一下这四个分别是什么。

  1. base：这个很好理解，就是把n维数组转换为一个一维数组，base是它需要的基地址。
  2. dim：字面意思，就是这个数组的维度。
  3. bounds：这个是一个一维数组，这个数组用来存放的每一个维度有多少个低一级维度的元素。

举个例子：二维数组a[m][n]，这就表示a数组有m个二维元素，每个二维元素有n个一维元素。 如果是n维数组：a[j1][j2]…[jn]，就表示a数组有j1个n维元素，每个n维元素有j2个n-1维元素，每个n-1维度又有j3个n-2维元素。 这里bounds的长度就是**dim**，那bounds[0]表示的就是dim维元素的个数，bounds[dim-1]表示的就是每个二维数组有多少个一维元素。

  1. constants:这个也是一个一维数组，这个数组用于存储上述表达式中的ci。

基本操作（可忽略）

  • 初始化操作
    1. Status InitArray(Array &A,int dim,....){                         //...表示这个是可变参数，至于这个是什么之后再讲
    2.   if(dim<1|[dim>MAX_ARRAY_DIM) return ERROR;                   //判断传入的参数是否符合规范，MAX_ARRAY_DIM是自定义的
    3.   A.dim=dim;
    4.   A.bounds=(int *)malloc(dim*sizeof(int));                     //给bounds数组的基地址赋值。
    5.   if(!A.bounds) exit(OVERFLOW);                    
    6.   elemtotal=1 ；                                               //elemtotal用于计算dim维数组的元素总个数。
    7.   va_tart(ap,dim);                                             //表示用ap指向dim后面的一个参数，就是...里面的参数
    8.   for(i=0;i<dim;++i){                                          //循环遍历每一个维度，获取每个维度的长度。
    9.       A.bounds[il=va_arg(ap,int);                              //定义...传入的参数是int类型，赋值给A.bounds[i]后，
    10.       if(A.bounds[i]<0) return UNDERFLOW;                      //ap指向下一个参数。
    11.       elemtotal*=A.bounds[i];                                  //n维元素的总个数就是每一维元素长度累计相乘。
    12.   }
    13.   va_end(ap);                                                  //结束可变参数函数参数的遍历
    14.   A.base=(ElemType*)malloc(elemtotal*sizeof(ElemType));        //给n维度数组的基地址赋值
    15.   if(!A.base) exit(OVERFLOW);
    16.   A.constants=(int*)malloc(dim*sizeof(int));                   //这里可以理解成给数组c的基地址赋值
    17.   if(!A.constants) exit(OVERFLOW);
    18.   A.constants[dim-1]=1;                                        //假设上述的L的值是1
    19.   for(i=dim-2,i>=0;--i)
    20.       A.constants[i]=A.bounds[i+1]*A.constants[i+1];           //等同上述表达式中的ci-1 = bi*ci
    21.   return OK;
    22. }

    这里的va_tart(ap,dim);和va_end(ap);必须绑定存在。

这里举个例子解释一下可变参数。
比如我要用初始化操作初始化一个二维数组，那我可以在代码里面这么写:

  1. Array A;
  2. InitArray(&A,2,3,4)；

&A是传入的未初始化的数组。 2表示维度，说明A数组是一个二维数组。 3和4可以看如下代码。

  1. va_tart(ap,dim);                                             //表示用ap指向dim后面的一个参数，就是...里面的参数
  2.     for(i=0;i<dim;++i){                                          //循环遍历每一个维度，获取每个维度的长度。
  3.         A.bounds[il=va_arg(ap,int);                              //定义...传入的参数是int类型，赋值给A.bounds[i]后，
  4.         if(A.bounds[i]<0) return UNDERFLOW;                      //ap指向下一个参数。
  5.         elemtotal*=A.bounds[i];                                  //n维元素的总个数就是每一维元素长度累计相乘。
  6.     }
  7.     va_end(ap);                                                  //结束可变参数函数参数的遍历

这里ap指向的的dim（也就是2这个参数）后面的参数，也就是3,所以bounds[0]=3，也就是A数组有3个二维元素。 经过一次遍历之后ap指向的的3这个参数后面的参数，也就是4，所以bounds[1]=4，也就是A数组有4个一维元素。 经过第二遍历后结束。 为什么写…，因为不同的dim需要后续传入的参数的个数是未知的。

小结：

  • n维数组的特点
    • n维数组中含有b个数据元素;
    • 数据元素同属于一种数据类型;
    • 数组一旦被定义，则维数和各维长度不能改变;
    • 数组是多维结构，但存储空间是一维结构。
  • 数组顺序表示的特点
    • 存储单元地址连续（需要一段连续空间)
    • 存储规则(以行（列）为主序）决定元素实际存储位置
    • 随机存取
    • 存储密度最大(100%)

4.4 压缩矩阵

  • 压缩存储:为多个值相同的元素只分配一个存储空间，对零元素不分配空间。
  • 目的:节省存储空间
  • 任务:压缩存储矩阵并使矩阵的运算有效进行。矩阵的存储:二维数组
  • 可压缩存储的矩阵有两类:
    • 特殊矩阵:值相同的元素或零元素在矩阵中分布有一定规律。如三角矩阵、对角矩阵。
    • 随机稀疏矩阵:值相同的元素或零元素在矩阵中分布没有一定规律

      特殊矩阵

      对称矩阵

      n阶矩阵A中元素满足性质a[i][j]=a[j][i](1≤i,j≤n)。
      image.png
      压缩存储:

      为每一对对称元素分配一个存储空间.n(n+1)/2 sa[k](O<k≤n(n+1)/2-1)为对称矩阵的压缩存储结构 这里的sa[k]表示把矩阵（类似一个二维数组）用一维数组来存储数据。

sa[k]结构：
image.png
a[i][j]在sa[k]结构里面的索引是：

  1. k = i(i-1)/2+j-1  (i≤j)(下三角元素)
  2. k = j(j-1)/2+i-1  (i<j)上三角元素)

上（下）三角矩阵

定义：矩阵下(上)三角(不含对角线)元素为常数c或0的n阶矩阵。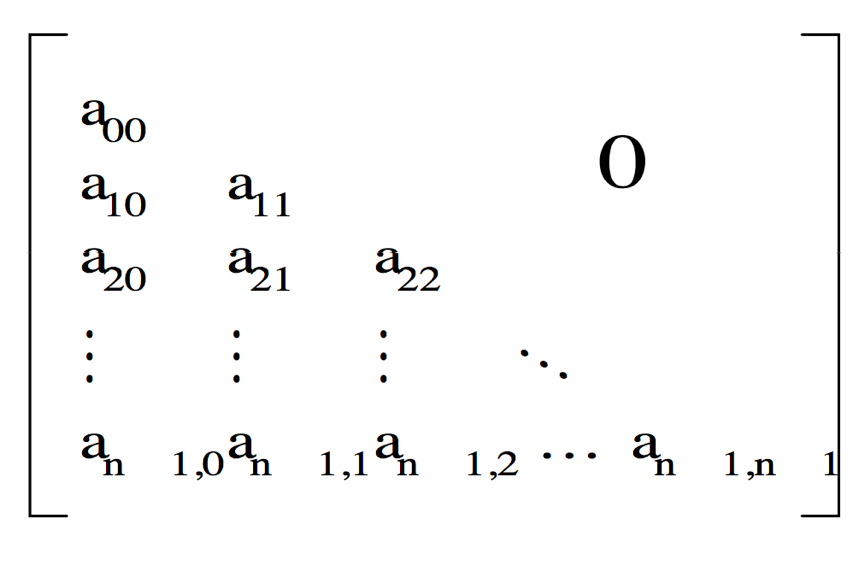
第四章：数组和广义表 - 图4
压缩存储:

存储上(下)三角中的元素和常数c。n(n+1)/2+1 sa[k](O<k≤n(n+1)/2)为上(下)三角阵的压缩存储结构 这里的0也可以是其他常数。

a[i][j]在sa[k]结构里面的索引是：

  1. //下三角矩阵
  2. k = i(i-1)/2+j-1  (i≤j)(下三角元素)
  3. k = n*(n+1)/2  (i<j)上三角元素)
  4. //上三角矩阵
  5. k = (i-1) (2n-i+2)/2+j-i (i≤j)
  6. k=n*(n+1)/2  (i>j)

对角矩阵

所有非零元素都集中在以主对角线为中心的带状区域。其他元素为0。
举个例子：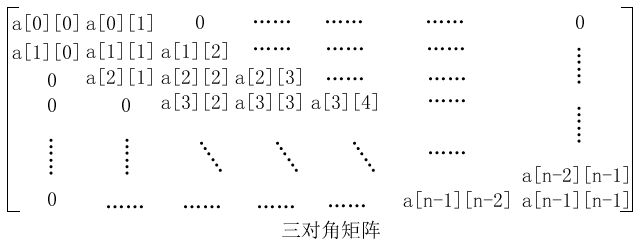
第四章：数组和广义表 - 图5
用行主序存储对角阵的元素。一共有**4＋3*(n-2)**个元素
sa[k](0≤k≤4+3*(n-2))为对角阵的压缩存储结构。

多一个是用于存储0。

不在第一行的非零元ai,j，它前面已经存储了前i-1行元素为2+3(i-2)

  • 若ai,j是本行需第1个存储的元素(ai,i-1)，k-3(i-1)-1，(j=i-1)
  • 若ai,j是本行需第2个存储的元素(ai,i)，k=3(i-1)，(i=j)
  • 若ai,j是本行需第3个存储的元素(ai,i+1)，k=3(i-1)+1，(j=i+1)

三式合并有k=2(i-1)+j-1。

练习题

1 设5对角矩阵A=(ai,j)2020(i，j从1开始)以行主序存放。按特殊矩阵压缩存储的方式将其5条对角线上的元素存入B[-10：m]中，计算元素a15,15的存储位置。
2 将一个A[1…100][1…100]的*三对角矩阵按行优先存于一维数组B[1,…298]中，A[66][65]在B中的位置为 。

解1：5对角阵A=(ai,j)2020第一行和第20行分别有3个元素，第二行和第19行有4个元素，其余各行分别有5个元素， a15,15是第**(31+41+512+3)=70个元素，存储位置70-10-1=59
解2：LOC(A[66][65])=2(i-1)+j-1+1=265+65=195**

这里的+1是因为数组B的索引是从1开始的。

稀疏矩阵

定义

image.png

模糊定义：就是一个矩阵中存在大量的0，所以用一个数组存储所有的非零元，用数组的最后一个元素来存储0。

image.png

由于有效的元素（也就是非零的元素）比较少，所以稀疏矩阵通常把有效元素在二维数组中的坐标i，j和其值e作为一个三元组存储。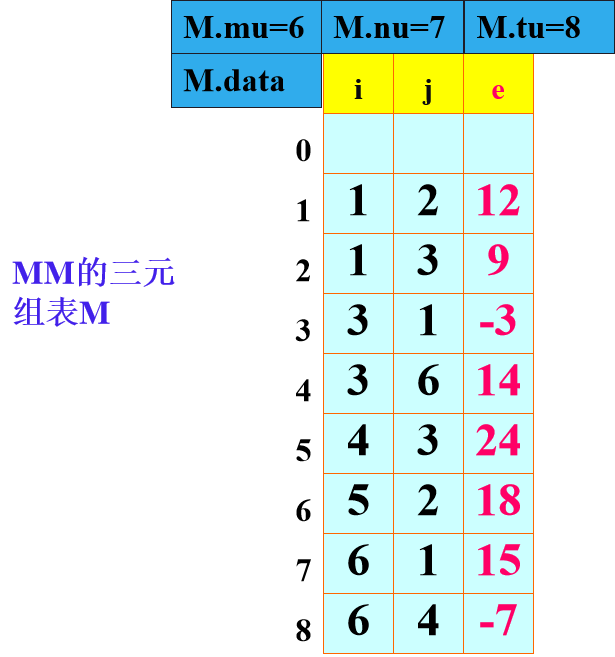
image.png
比如第1个就代表第1行第2列有个值为12的元素。

上面的6/7/8分别代表，数组有6行、7列以及三元组所需要的存储空间为8（因为0元素需要单独一个存储空间）。

三元组的C语言描述

  1. typedef struct {
  2.     int i,j;
  3.     ElemType e;
  4. }Triple

e表示的非零元的值 i,j分别为e元素的下标

三元组顺序表的C语言表述

  1. #define MAXSIZE 125000
  2. typedef struct{
  3.     Triple data[MAXSIZE+1]; //data[0]未用
  4.     int mu,nu,tu;
  5. }TSMatrix

mu，nu，tu分别表示的是矩阵的行数，列数，和非零元的个数。 data数组中每一个元素都是Triple类型的数据。

使用稀疏矩阵的三元组顺序表来实现矩阵的转置

  • 矩阵转置的经典算法

假设Tn*m是Mm*n的转置矩阵。

  1. for(col=1;col<=n;++col){
  2.     for(row=1;row<=m;++row){
  3.         T[col][row]=M[row][col];
  4.     }
  5. }
  • 转置步骤：
    • 将矩阵行列值(即m和n)相互交换
    • 将每个三元组中的i和j对换
    • 重排三元组的次序
  • 算法实现
    1. Status TransposeSMatrix(TSMatrix M,TSMatrix &T){            //传入被转置的矩阵M，已经一个空矩阵T作为转置后的矩阵
    2.   T.mu=M.nu;T.nu=M.mu;T.tu=M.tu;                          //使T矩阵的行数（列数）等于M矩阵的列数（行数）
    3.   if(T.tu){                                               //判断T矩阵为非零矩阵。
    4.       q=1;                                                
    5.       for(col=1;co<=M.nu;++col){                          //从列开始遍历，把每一列中的非零元赋值到T的相应的行的位置上。
    6.           for(p=1;p<=M.tu;++p){                           //遍历所有的非零元
    7.               if(M.data[p].j=col){                        //当M中第p个非零元的列数等于遍历的列数
    8.                   T.data[q].i=M.data[p].j;                //就把该元素进行转置操作
    9.                   T.data[q].j=M.data[p].i;
    10.                   T.data[q].e=M.data[p].e;
    11.                   ++q;                                    //T的压缩存储结构与M相同，所以从1开始给T的存储结构赋值
    12.                   }                                       //每赋值一次q++，用来赋值下一个元素。
    13.               }
    14.       }
    15.   return OK;
    16. }//TrvansposeSMatrix
    实例算法分析

    这里的&T是因为要修改T矩阵，所以要加上&

假设M矩阵如下，转置后矩阵T也如下

  1. M:
  2. {  1   0   0
  3.    0   0   1
  4.    0   0   0}
  5. T:
  6. {  1   0   0
  7.    0   0   0
  8.    0   1   0
  9. }

按照算法来分析：

  1. M矩阵的行数为3，列数为3，非零元有两个，所以M.nu=3,M.mu=3,M.tu=3,M.data={0,1,1}
  2. 遍历第i列，一共有nu（3）个数，要找出非零的元素进行转置，也就是只有在data中元素的列数=i，表示该元素在第i列上。
  3. 例如这里的第一列，一共三个数{1,0,0}，在data数组中只有a[1]=1符合条件，所以将a[1]进行转置。
  4. 反复遍历直至所有行和列都遍历完，也就完成了转置。

    缺点：只有在*tu远小于munu的时候才适合用。 算法复杂度：O(nutu)

4.5 广义表

定义

讲人话就是表里面嵌套表
举个例子：

  1. (1,2,(3,4,5),6,(7,(8,9)))
  • 表头(head):n>0时,表的第一个表元素
  • 表尾(tail):除去第一个表元素其它表元素组成的表
  • 空表:n=0的广义表。
  • 广义表的特性:
    • 有长度:n（最外面括号下面的元素或者表的个数的总和）
    • 有深度:广义表中括号的重数（最多的层数）
    • 可递归

      上述例子中，长度为5，深度为3。 非空列表表头可是原子或列表,表尾必定是列表

图形表示

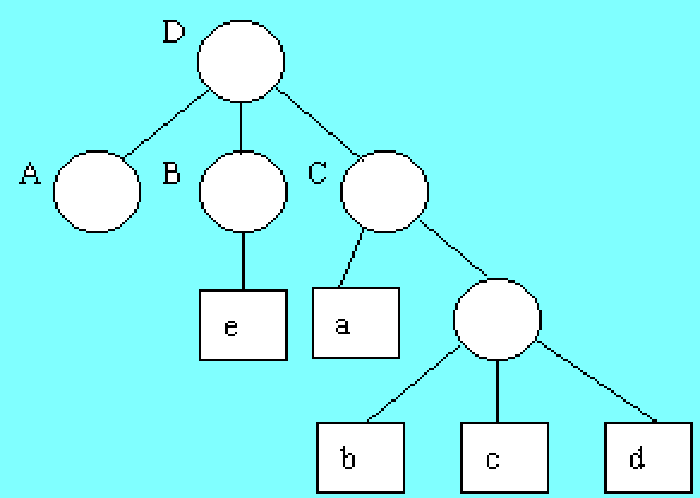
image.png
1、A=(/)
2、B=(e)
3、C=(a,(b,c,d))
4、D=(A，B，C)

注：○：表□：原子

什么是广义表、广义表及定义详解