第五章：分类

分类的基本概念

什么是分类

分类（classification）：分类任务就是通过学习得到一个目标函数（target funciton）f, 把每一个属性集 x 映射到一个预先定义的类标号y。目标函数也称为分类模型（classification model）。
举个缀简单的例子：有一批学生的数据集，通过学习得到了一个分辨男女生的目标函数，这里每一个学生就是x，男女分别是y1，y2，这个目标函数的目的就是把x映射到y = {y1,y2}，这个集合上。

如何进行分类

数据分类是一个两阶段的过程，包括学习阶段（构建分类器/模型）和分类阶段（使用模型预测给定数据的类标号）。
在第一阶段，建立描述预先定义的数据类和概念集的分类器。这是学习阶段（或训练阶段），其中分类算法通过分析或从训练接“学习”来构造分类器。训练集是有数据和与它相关联的类标号组成。分类过程的第一个阶段可以看成是学习一个映射或函数y=f(x) ，它可以预测给定数据 x 的类标号 y。
在第二个阶段，使用模型进行分类。使用有检验数据和与它们相关联的 类标号组成的检验集（test set）。

这就类似于一个初始的数据集，按照比例分为训练集和测试集（比如训练集占60%，测试集占40%）。
首先使用训练集进行学习，训练出来一个模型（函数）。
然后就是使用测试集来测试模型的精准度。

KNN算法介绍

基本原理

KNN是K Nearest Neighbor，意思是 **K**个最近的邻居，KNN的原理就是当预测一个新的值x 的时候，根据它距离最近的K个点是什么类别来判断x 属于哪个类别。如图所示：

原理非常的简单，比如上图中三角形和圆形是已经确定类型，假设数据集中只有这两种类别的数据，我们分别称之：

• 三角形：类别1
• 圆形：类别2

正方形是需要预测的类型，KNN算法的原理就是，当K=3的时候，寻找距离正方形最近的3个点，并且判别他们的类型，哪个类型多，那么正方形就越有可能是哪个类型。左图中很明显能看出来，距离正方形最近的三个点中，有两个是三角形，有一个是圆形，所以这里判定正方形的类型应该就是三角形的类型，也就是类别1。
这种谁多就是谁的方法，叫做多数表决规则。

KNN算法三要素

• 距离度量
• K值
• 分类决策规则

距离计算

欧式距离

这里最常用的也就是欧式距离：
二维平面上的时候

更高维度上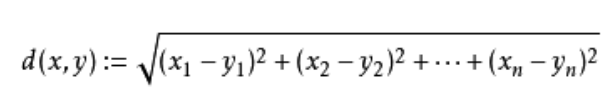

当然PPT上面介绍了很多花里胡哨的距离，这里就简单介绍一下：

曼哈顿距离

切比雪夫距离

二个点之间的距离定义是其各坐标数值差绝对值的最大值。

闵可夫斯基距离

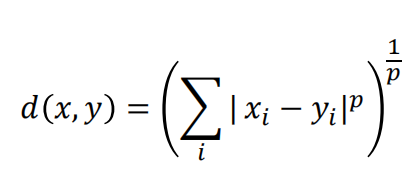
• 𝑝取1或2时的闵氏距离是最为常用的
• 𝑝 = 2即为欧氏距离，
• 𝑝 = 1时则为曼哈顿距离。
• 当𝑝取无穷时的极限情况下，可以得到切比雪夫距离

  K值选择

  不难看出，KNN算法里面最关键的就是K的取值，因为只有K的取值影响了最终判断的结果。而K的取值不是一下子就能确定的，需要不断的重复和尝试，尝试的方法就是交叉验证。
  将样本数据按照一定比例，拆分出训练用的数据和验证用的数据，比如6：4拆分出部分训练数据和验证数据，从选取一个较小（一般是1）的 K 值开始，不断增加 K 的值，然后计算验证集合（测试集）的错误率，最终找到一个比较合适的K 值。
  最终我们可以获得一张类似下面的图：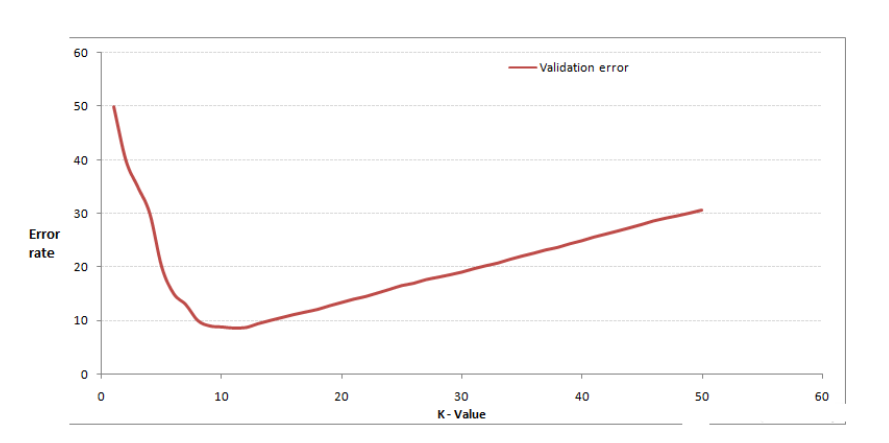
  
  很明显，这里当K=10的时候，错误率比较低，也就说准确率比较高，模型比较好，分类准确。

  就是咱也不知道就非要算错误率，直接算准确率不香嘛。

而这个错误率的计算就是下面模型评估的内容了。

模型评估与选择

模型评价指标

度量方法

所谓模型评估，简单来讲就是希望评估该分类器预测未来的数据（未经过训练的数据）的准确率。
模型评估通常常用的度量方法包括：

• 准确率（识别率 accuracy）
• 敏感度（或者成为召回率 recall）
• 特效性
• 精度（precision）
• F**1和Fβ**

正负元组

这些度量方法就需要引入一个定义：

• 正元组：感兴趣的主要类的元组（样本）
• 负元组：其他元组（样本）
• P：正元组数
• N：负元组数

定义很抽象，我举个例子就懂了：
还是上面的学生集区分男女生的例子，比如我们希望预测到的样本是男生，如果我们拿到一个男生的样本，这个样本就是所谓的正元组，如果我们拿到一个女生的样本，那么这个样本就是所谓的负元组，反过来也是一样的。
那如果拓展到多个类别，比如我们希望预测到的样本是类别A，如果我们拿到一个类别A的样本，这个样本就是所谓的正元组，如果我们拿到一个其他类别的样本，那么这个样本就是所谓的负元组。

其他概念

• 真正例/真阳性：是指被分类器正确分类的正元组。令 TP 为真正例的个数。
• 真负例/真阴性：是指被分类器正确分类的负元组。令 TN 为真负例的个数。
• 假正例/假阳性：是指被错误地标记为正元组的负元组。令 FP 为假正例的个数。
• 假负例/假阴性：是指被错误地标记为负元组的正元组。令 FN 为假负例的个数。

还是举个例子：
还是上面的学生集区分男女生的例子，比如我们希望预测到的样本是男生，那么：

• 正元组：男生
• 负元组：女生
• 真正例/真阳性：被分类器分辨为男生的男生。
• 真负例/真阴性：被分类器分辨为女生的女生。
• 假正例/假阳性：被分类器分辨为男生的女生。
• 假负例/假阴性：被分类器分辨为女生的男生。 | 实际值\ 预测值 | 男生 | 女生 | | —- | —- | —- | | 男生 | 真阳性 | 假阴性 | | 女生 | 假阳性 | 真阴性 |

计算性质如下：

• P+N = 样本总数
• TP + FN = P
• FP + TN = N

  度量方法的计算

  

  其中precision就是准确率。 其中recall就是召回率。

重点是这位重量级：

ROC曲线

ROC 曲线是一种比较两个分类模型有用的可视化工具。
ROC 曲线显示了给定模型的真正例率（TPR）和假正例率（FPR）之间的 权衡。给定一个检验集合模型:

• TPR 是该模型正确标记的正元组的比例；
• FPR 是该模型错误标记的负元组的比例。
• TPR = TP / P
• FPR = FP / N

如果有多组测试样本，就可以得到下面这张表：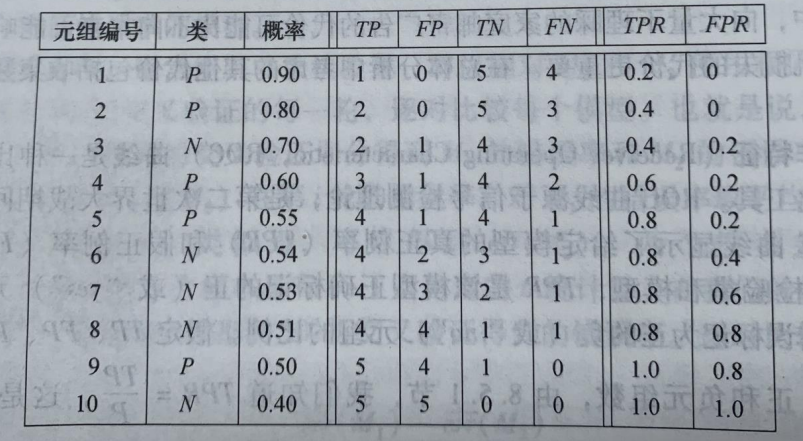

以FPR为X轴，TPR为Y轴，那么就可以得到下面这张图：

当曲线和X轴围成的面积越大的时候，模型越准确。

决策树分类

什么是决策树

定义

首先看一下官方定义：
决策树是一种类似于流程图的树结构，其中，每一个内部节点（非树叶节点）表示在一个属性上的测试，每个分支代表该测试的一个输出，而每个叶子结点（或中断结点）存放一个类标号。树的最顶层结点是根结点。
其实简单的来讲就是通过不断对特征进行判断对样本进行分类。

原理

下面这张图就很好的解释了决策树的原理，其中椭圆部分就是样本的特征：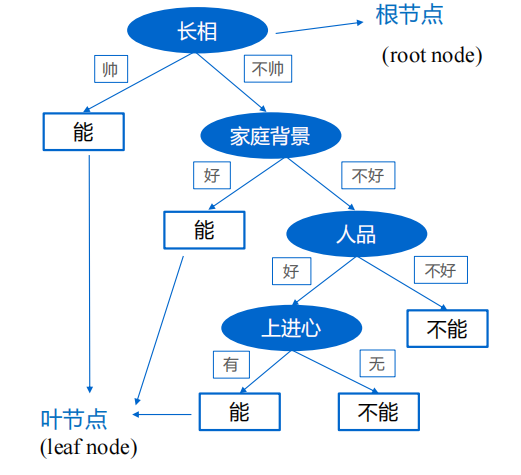

从上图中我们不难看出，一个样本的特征有四个，分别是长相，家庭背景，人品，上进心。

上面这张图非常的直观，我就不多介绍了。
决策树的决策过程就是从根节点开始，测试待分类项中对应的特征属性，并按照其值选择输出分支，直到叶子节点，将叶子节点的存放的类别作为决策结果。

在大概知道决策树的运算流程之后，我们能知道哪个特征作为根节点非常重要，这个在后面会讲解选择哪一个特征作为根节点。

相关概念

下面一张图解决：

决策树的性质

• 决策树属于判别模型
• 决策树算法属于监督学习方法
• 决策树归纳的基本算法是贪心算法，自顶向下来构建决策树
• 贪心算法：在每一步选择中都采取在当前状态下最好/优的选择
• 在决策树的生成过程中，分割方法即属性选择的度量是关键

决策树的特点

优点：

• 推理过程容易理解，计算简单，可解释性强。
• 比较适合处理有缺失属性的样本。
• 可自动忽略目标变量没有贡献的属性变量，也为判断属性变量的重要性，减少变量的数目提供参考。

缺点：

• 容易造成过拟合，需要采用剪枝操作。
• 忽略了数据之间的相关性。
• 对于各类别样本数量不一致的数据，信息增益会偏向于那些更多数值的特征

  信息论相关概念

  在学习具体的算法之前，需要知道信息论的相关概念。
  我们先用一个例子来方便后面的讲解：

  最后分类的结果是是否打球。

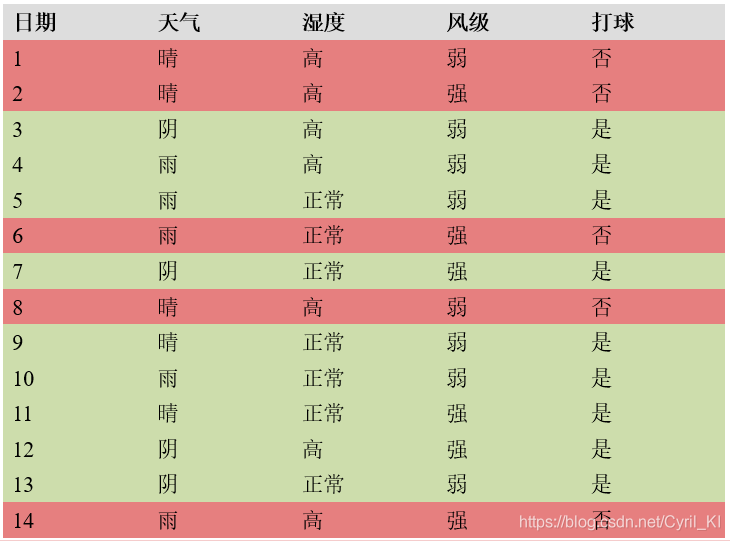
信息熵

所谓信息熵，就是用于描述信息的混乱程度的，信息熵越低的时候，说明信息越一致，也就是我们分类的目标。

首先申明一点，信息熵的计算有两种：

• 总体样本的信息熵
• 根据特征分类样本的信息熵

公式的解析：

• H(Y)：信息熵
• pi：简单来讲pi可以理解为事件的概率（后面例子中会讲）
• Y：目标值
• m：目标值离散值的最大个数（比如这里只能取是和否，所以m就是2）
• 通常log的底数是**2**，一般都省略

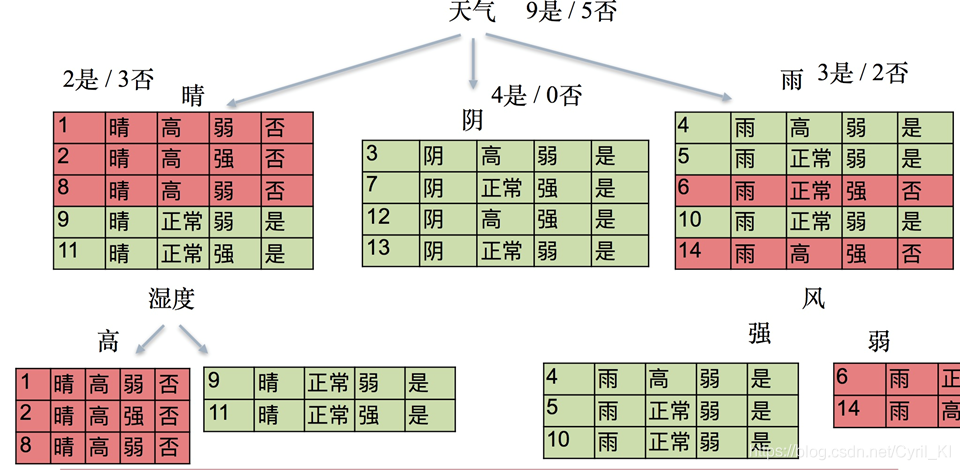
首先来看总体的信息熵：拿最开始还未分类的总体样本计算。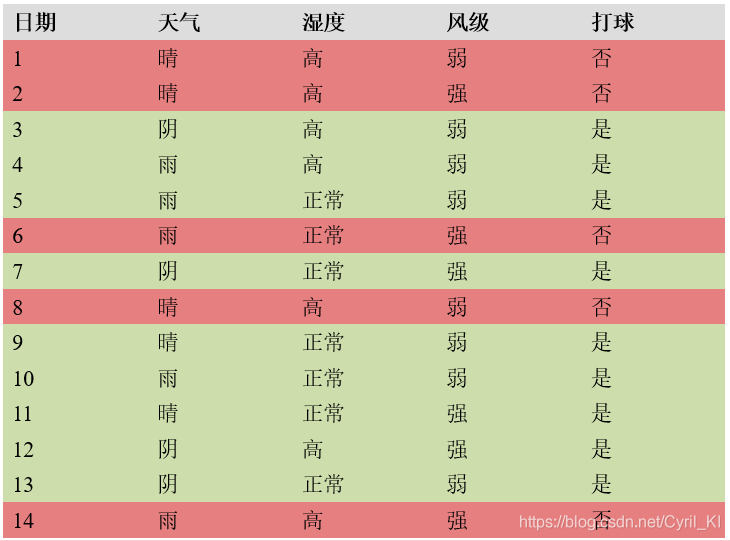

可以看到总样本量是14，结果为是的样本有9份，否的有5份。
那么p1 = 9/14，p2 = 5/14。
代入公式可得整体的信息熵为：
H0=−[(5/14)log5/14+(9/14)log9/14]=0.9403

那么同理，我们计算第一次分类之后的结果，计算根据天气分类之后的各组样本的信息熵：

• 晴：被分为5份，2是/3否，它的信息熵为：
  • H1 = −[(2/5)log2/5 + (3/5)lo3/5 ] = 0.9710
• 阴：被分为4份，4是/0否，它的信息熵为：
  • H2 = −[log1] = 0
• 雨：被分为5份，3是/2否，它的信息熵为：
  • H3 = − [(2/5)log2/5 + (3/5)log3/5 ] = 0.9710

    加权信息熵

    接着可以根据分类之后的样本量/分类之前的总样本量作为权重，获取加权信息熵：
    H′=5/14H1+4/14H2+5/14H3=0.6936
    这可以就可以作为第一次分类之后的总信息熵。

信息增益（重点）

g(D,A)就是信息增益，其中D表示的是总样本，A表示某一个特征。

其余的概念小节末会放置链接。

最直白概念，其实就是分类前的信息熵减去分类后的信息熵即可。
比如：
H0−H′=0.9403−0.6936=0.2467
也就是说当这个信息增益越大的时候，我们越容易得到更一致的数据。
其实这里也就解释了决策树的缺点里面的最后一点：信息增益会偏向于那些更多数值的特征。
因为当特征的取值较多时，根据此特征划分更容易得到纯度更高（也就是之前说的更加一致）的子集，因此划分之后的熵更低，由于划分前的熵是一定的，因此信息增益更大，因此信息增益比较偏向取值较多的特征。

信息增益率（重点）

也就是信息增益率 = 信息增益 / 分类后A特征的信息熵
注意，这里H函数的参数不是Y了而是A（特征值）。
还是用上面的举例子，那么A就是天气这个特征：
其中信息增益g(D,A) = 0.6936已经计算得出，接下来只要计算H(A)即可，这里的计算和上面对加权信息熵的计算很相似，只不过计算的标准从打球切换到了天气，计算过程类似：
H(A)=−[(5/14)log5/14+(4/14)log4/14+(5/14)log5/14]=1.5774
最后简单做一个除法即可：
gr(D,A)=g(D,A)/H(A)=0.2467/1.5774=0.1566

Gini系数（重点）

所谓Gini系数指的就是在样本集合中一个随机选中的样本被分错的概率。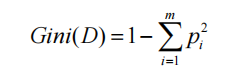

参数说明：

1. pi表示选中的样本属于第i类别的概率。
2. 样本集合中有m个类别，一个随机选中的样本可以属于这m个类别中的任意一个。
3. 易知，当样本属于每一个类别的概率都相等即均为**1/m**时，基尼系数最大，也就是说此时不确定度最小。

   这里就不做举例了，因为PPT讲义还有原文都没有计算，我也不想算哈哈哈哈。

本小节原文地址

决策树与随机森林(从入门到精通)Cyril_KI的博客-CSDN博客关于决策树与随机森林的描述正确的是

决策树三种算法

三种算法的核心都是根据各指标，进行需要划分特征的选择。

ID3算法

ID3算法采用的指标就是信息增益，特点如下:

• ID3 没有剪枝策略，容易过拟合；
• 信息增益准则对可取值数目较多的特征有所偏好，类似“编号”的特征,其信息增益接近于 1；
• 只能用于处理离散分布的特征；
• 没有考虑缺失值。

C4.5算法

C4.5算法采用的指标就是信息增益率，特点如下：

• 在决策树构造过程中进行剪枝。
• 对非离散数据也能处理。
• 能够对不完整数据进行处理。

CART算法

CART算法采用的指标就是基尼指数，特点如下：

• 顾名思义，CART算法既可以用于创建分类树，也可以用于创建回归树，两者在构建的过程中稍有差异。
• 如果目标变量是离散的，称为分类树。
• 如果目标变量是连续的，称为回归树。