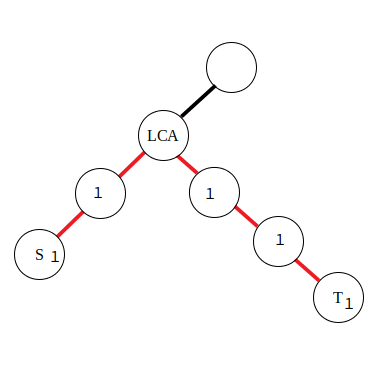
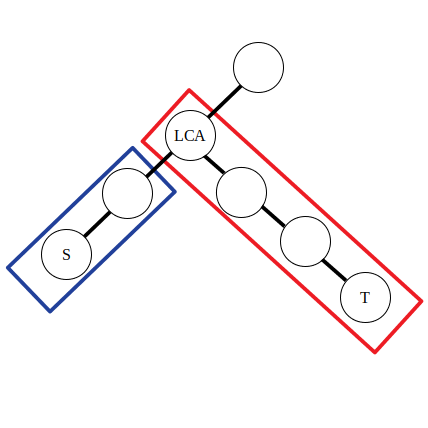
在“前缀和 与 差分”中，我们定义了一个序列的前缀和与差分序列，并通过差分技巧，把“区间”的增减转化为“左端点加1，右端点减1”。根据“差分序列的前缀和是原序列”这一原理，在树上可以进行类似的简化，其中“区间操作”对应为“路径操作”，“前缀和”对应为“子树和”。

树上差分可以理解为对树上的某一段路径进行差分操作，这里的路径可以类比一维数组的区间进行理解。例如在对树上的一些路径进行频繁操作，并且询问某条边或者某个点在经过操作后的值的时候，就可以运用树上差分思想了。

树上差分通常会结合 树基础 和 最近公共祖先 来进行考察。树上差分又分为 点差分 与 边差分，在实现上会稍有不同。

  1. 差分，通俗一点就是把区间的操作改为点操作，在点上记录变化量。

边差分

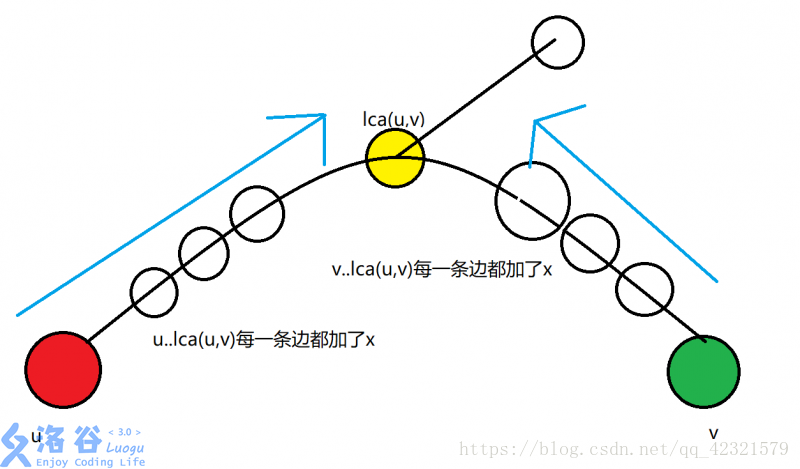
image.png

  1. 我们给树上每个结点一个初始为 0 的权值，
  2. 然后对结点 x 的权值加 1，结点 y 的权值加 1， 
  3. 结点LCA(x, y)的权值减 2.
  5. 最后对这棵生成树进行一次深度优先遍历，求出 F[x] 表示以 x 为根的子树中各结点的权值之和。 
  7. 时间复杂度是 O(n + m)
  1. 边差分：
  3. 边差分的话要把边的权值存在他连着的儿子节点上，
  4. 然后儿子节点的权值就是这条边的边权了，
  6. u至v路径上所有边的边权+1，
  7. 那么c[u]++,c[v]++,c[lca]-=2,可以在多次更新树链之后，得到某边权值。
  1. 例如，有一次操作是把红点（u）到绿点（v）之间的路径全部加x。
  2. 那么我就标记dlt[u]+=x,dlt[v]+=x。
  4. 这样在最后求解的时候，回溯的时候顺便算一下答案就出来了。
  6. 然后我们要在lca(u,v)处标记dlt[lca(u,v)]-=2x。
  8. 这样就使得加x的效果只局限在u..v，不会向lca(u,v)的爸爸蔓延。

image.png
image.png
image.png

例题，Fools and Roads

点差分

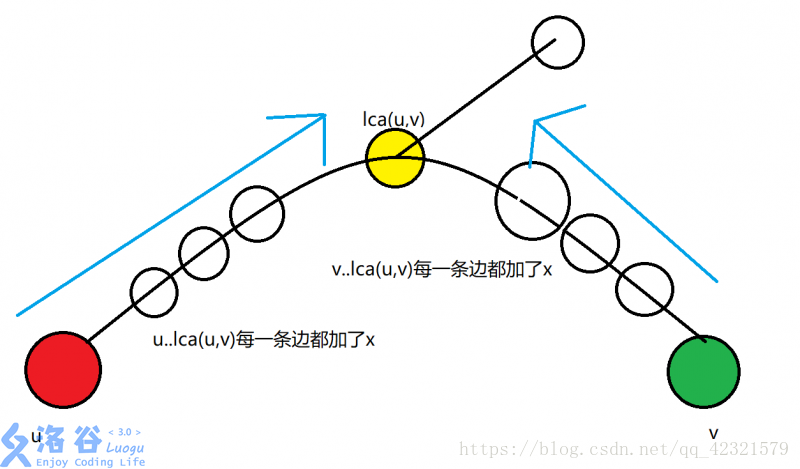
image.png

  1. 点差分：
  2. u至v路径上所有点点权+1，那么
  3. c[u]++,c[v]++,c[lca]--,c[fa[lca]]--,
  4. 可以在多次更新树链的点之后，得到某点权值
  6. 做法也是和边差分稍有不同，我们不在dlt[lca(u,v)]-=2x，
  7. 而是把dlt[lca(u,v)]-=x，并把dlt[fa[lca(u,v)]]-=x。
  9. 为什么呢？因为lca(u,v)也在u..v这条路径上，它同样需要被加x。
  11. 回溯的时候会从u和v两个方向都给lca(u,v)加一个x，而它只能加一个，因此dlt[lca(u,v)]-=x。
  12. 而lca(u,v)的爸爸则根本无法被加，在lca(u,v)已经只加一个x了，
  13. 因此dlt[fa[lca(u,v)]]-=x就能让lca(u,v)的爸爸不加x。

image.png
image.png

例题，P3128 [USACO15DEC]Max Flow P