depth-first search and breadth-first search. Both algorithms are given a starting node in the graph, and they visit all nodes that can be reached from the starting node. The difference in the algorithms is the order in which they visit the nodes.

Depth-first search深度优先遍历

Depth-first search always follows a single path in the graph as long as it finds new nodes. After this, it returns to previous nodes and begins to explore other parts of the graph. The algorithm keeps track of visited nodes, so that it processes each node only once.

The neighbors of node 5 are 2 and 3, but the search has already visited both of them, so it is time to return to the previous nodes. Also the neighbors of nodes 3 and 2 have been visited, so we next move from node 1 to node 4

The time complexity of depth-first search is O(n + m) where n is the number of nodes and m is the number of edges, because the algorithm processes each node and edge once.

vector<int> adj[N];
bool visited[N];
void dfs(int s) {
    if (visited[s]) return;
    visited[s] = true;
    // 遍历所有相邻的结点
    for (auto u: adj[s])
        dfs(u);
}

Breadth-first search宽度优先遍历

Breadth-first search (BFS) visits the nodes in increasing order of their distance from the starting node. Thus, we can calculate the distance from the starting node to all other nodes using breadth-first search.

Like in depth-first search, the time complexity of breadth-first search is O(n + m), where n is the number of nodes and m is the number of edges.

queue<int> q;
bool visited[N];
int distance[N];
visited[x] = true;
distance[x] = 0;
q.push(x);
while (!q.empty()) {
    int s = q.front(); q.pop();
    for (auto u : adj[s]) {
       if (visited[u]) continue;
       visited[u] = true;
       distance[u] = distance[s]+1;
       q.push(u);
    } 
}

例题，【例8.3】最少步数

//棋盘问题，最短路

例题，Dungeon Master

//棋盘问题，最短路

例题，仙岛求药

//棋盘问题，最短路，多组测试数据

洪水填充算法（floodfill）

例题，Lake Counting

//Flood Fill

例题，The Castle

//Flood Fill，位运算

Connectivity check图的连通性验证

从任意一个点出发，做dfs，可以判断这个图是否连通的。
通过这种方法，我们也可以用来统计图当中，有多少个独立的块。
从1…n遍历，如果一个点没遍历过，就dfs(bfs也可以)进去，遍历的时候进行标记。

A graph is connected if there is a path between any two nodes of the graph. Thus, we can check if a graph is connected by starting at an arbitrary(任意的) node and finding out if we can reach all other nodes. For example, in the graph a depth-first search from node 1 visits the following nodes: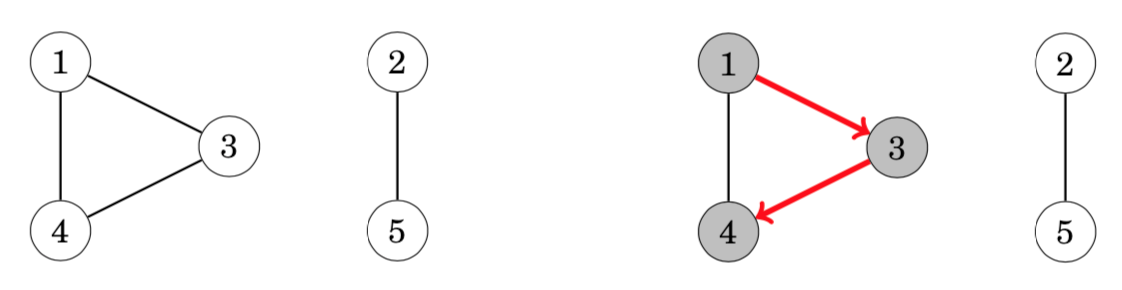

Since the search did not visit all the nodes, we can conclude that the graph is not connected. In a similar way, we can also find all connected components of a graph by iterating through the nodes and always starting a new depth-first search if the current node does not belong to any component yet.

Finding cycles判环

A graph contains a cycle if during a graph traversal, we find a node whose neighbor (other than the previous node in the current path) has already been visited. For example, the graph contains two cycles and we can find one of them as follows:

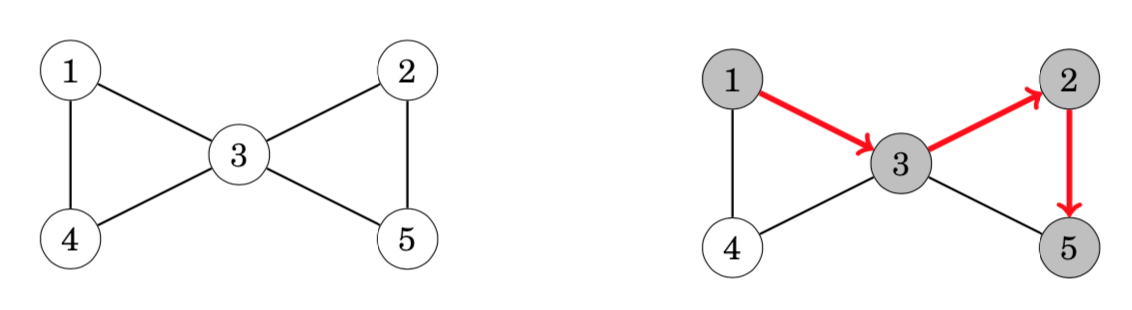
After moving from node 2 to node 5 we notice that the neighbor 3 of node 5 has already been visited. Thus, the graph contains a cycle that goes through node 3, for example, 3→2→5→3.

Another way to find out whether a graph contains a cycle is to simply calculate the number of nodes and edges in every component. If a component contains nodes and no cycle, it must contain exactly edges (so it has to be a tree). If there are _ _or more edges, the component surely contains a cycle.（如果 边数 >= n，那么 一定存在环）

Topological sorting拓扑序

A topological sort is an ordering of the nodes of a directed graph such that if there is a path from node a to node b, then node a appears before node b in the ordering. For example, for the graph one topological sort is [4,1,5,2,3,6]: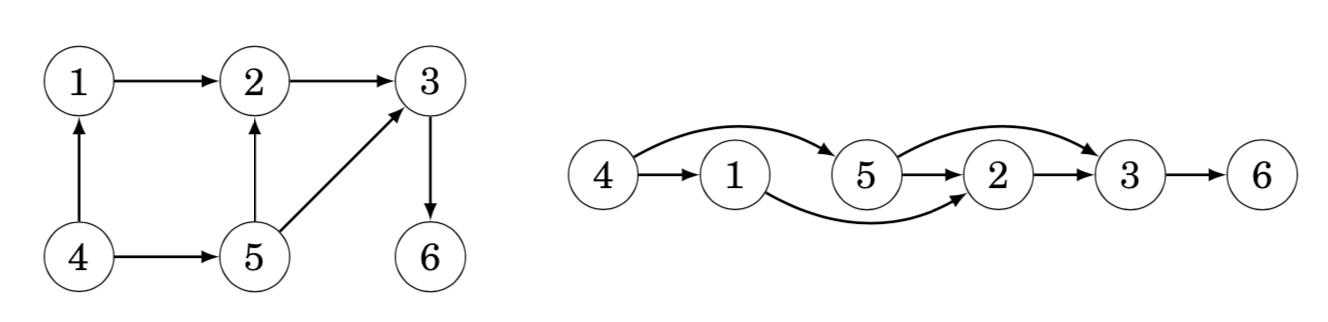

An acyclic(无环的) graph always has a topological sort. However, if the graph contains a cycle, it is not possible to form a topological sort, because no node of the cycle can appear before the other nodes of the cycle in the ordering. It turns out that depth-first search can be used to both check if a directed graph contains a cycle and, if it does not contain a cycle, to construct a topological sort.

1. topsort就是有向图的宽度优先遍历的应用
2. 拓扑序，不唯一
3. 如要要字典序最小的拓扑序，在遍历入度为0的点的时候，从1开始遍历，并入队
4. 有明显【层级关系】的问题，可以考虑用topsort()模型

例题，1964：【13NOIP普及组】车站分级

给出了m趟列车的停靠情况
每一个车站有一个级别
停靠的规则是，一旦停靠站A，那么后续经过的所有站，只要站的级别比A大，就要停靠
问，这n个车站，满足m趟停靠规则的前提下，最少需要区分出来几个级别
问题具有层级性

Paths and circuits路径和回路

An Eulerian path is a path that goes through each edge exactly once.
A Hamiltonian path is a path that visits each node exactly once.

While Eulerian and Hamiltonian paths look like similar concepts at first glance, the computational problems related to them are very different. It turns out that there is a simple rule that determines whether a graph contains an Eulerian path, and there is also an efficient algorithm to find such a path if it exists. On the contrary, checking the existence of a Hamiltonian path is a NP-hard problem, and no efficient algorithm is known for solving the problem.

什么是NP-hard问题?

Eulerian paths欧拉路径，一笔画问题

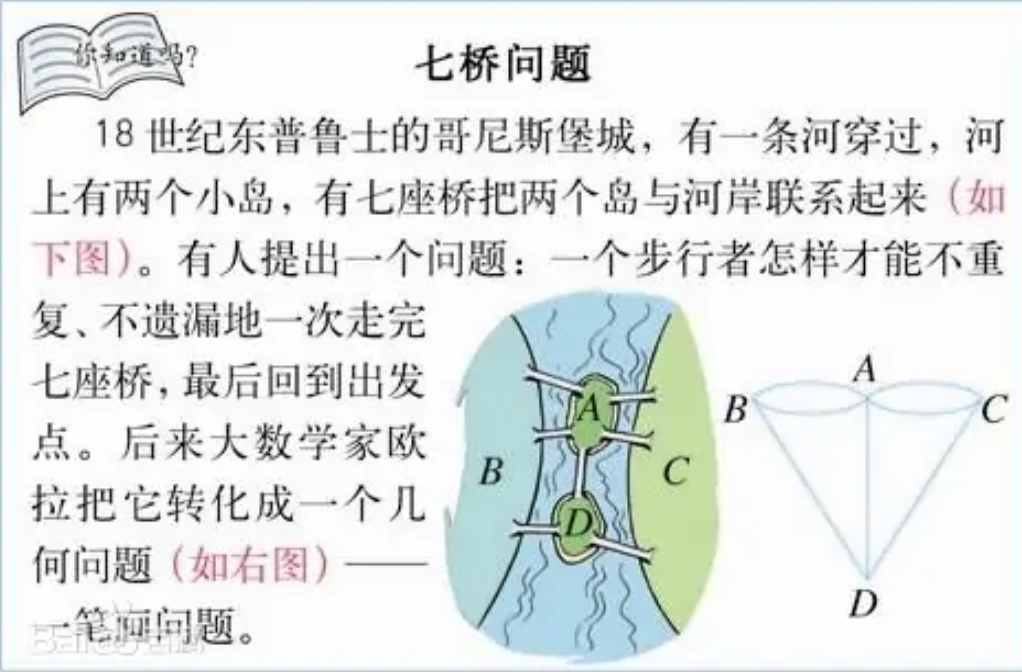
L. Euler studied such paths in 1736 when he solved the famous Königsberg bridge problem. This was the birth of graph theory.(七桥问题)

An Eulerian path(欧拉路径) is a path that goes exactly once through each edge of the graph. For example, the graph has an Eulerian path from node 2 to node 5:

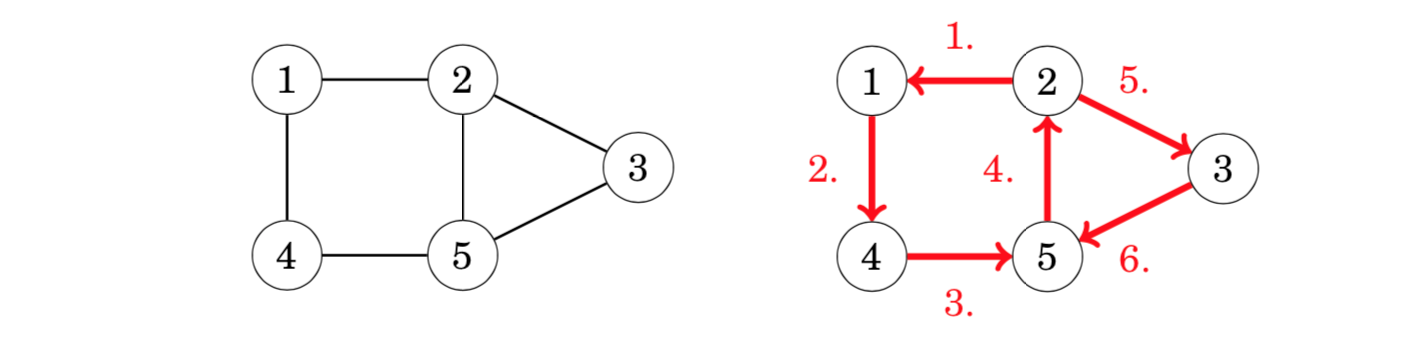
An Eulerian circuit(欧拉回路) is an Eulerian path that starts and ends at the same node. For example, the graph has an Eulerian circuit that starts and ends at node 1:

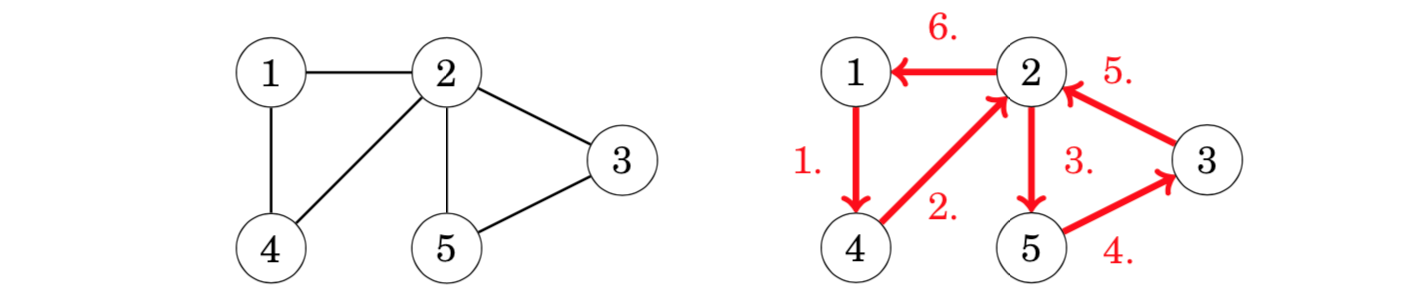
Existence

The existence of Eulerian paths and circuits depends on the degrees of the nodes. First, an undirected graph has an Eulerian path exactly when all the edges belong to the same connected component and

• the degree of each node is even(所有点的度数是偶数)(欧拉回路)
• the degree of exactly two nodes is odd, and the degree of all other nodes is even.(有两个点度数是奇数，其他所有点的度数是偶数)(欧拉路径)(奇数点就是起点)
• 以上两点满足其一

In the first case, each Eulerian path is also an Eulerian circuit. In the second case, the odd-degree nodes are the starting and ending nodes of an Eulerian path which is not an Eulerian circuit.

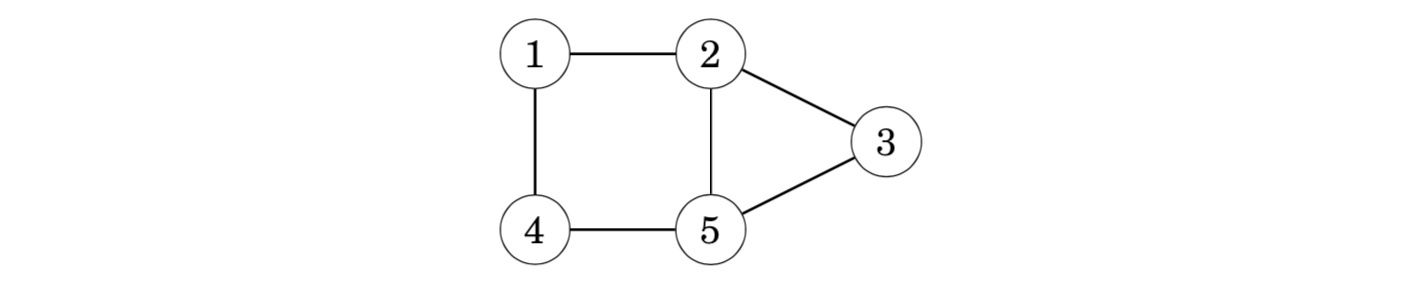
nodes 1, 3 and 4 have a degree of 2, and nodes 2 and 5 have a degree of 3. Exactly two nodes have an odd degree, so there is an Eulerian path between nodes 2 and 5, but the graph does not contain an Eulerian circuit.

In a directed graph, we focus on indegrees and outdegrees of the nodes. A directed graph contains an Eulerian path exactly when all the edges belong to the same connected component and

• in each node, the indegree equals the outdegree(所有点出度和入度相等)(欧拉回路)
• in one node, the indegree is one larger than the outdegree, in another node, the outdegree is one larger than the indegree, and in all other nodes, the indegree equals the outdegree.(一个点入度比出点大1，一个点出点比入度大1，其他点入度和出度相等)(欧拉路径)
• 以上两点满足其一

In the first case, each Eulerian path is also an Eulerian circuit, and in the second case, the graph contains an Eulerian path that begins at the node whose outdegree is larger and ends at the node whose indegree is larger.

nodes 1, 3 and 4 have both indegree 1 and outdegree 1, node 2 has indegree 1 and outdegree 2, and node 5 has indegree 2 and outdegree 1. Hence, the graph contains an Eulerian path from node 2 to node 5:

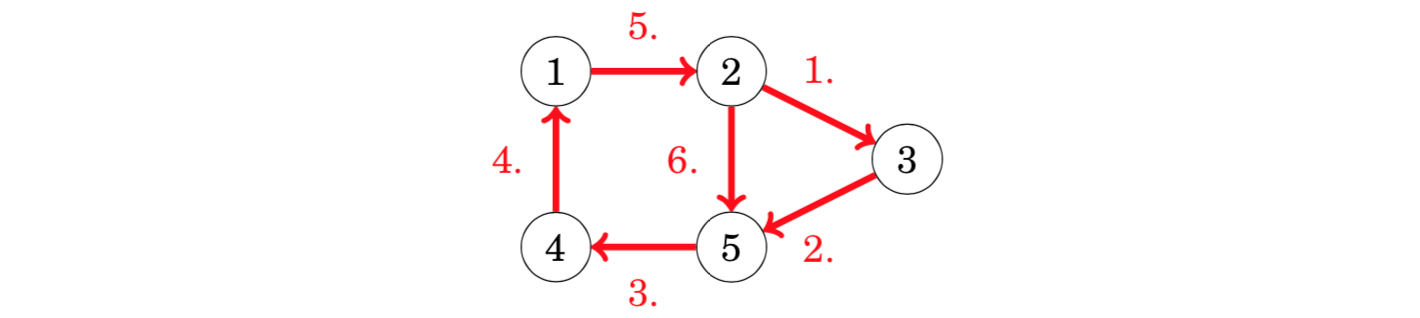
//示例代码，一笔画问题
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int g[N][N], in[N];
int n, m;
vector<int> path;
bool vis[N];
int circuit = 0;
void dfs(int u)
{
    path.push_back(u);
    for (int j = 1; j <= n; j++)
        if (g[u][j]){
            g[u][j] = g[j][u] = 0; //这条边画掉
            dfs(j);
            break;
        }
}
int main()
{
    cin >> n >> m;
    for (int i = 0; i < m; i++){
        int a, b;
        cin >> a >> b;
        g[a][b] = g[b][a] = 1;
        in[a]++; in[b]++;
    }
    int st = 1;
    for (int i = 1; i <= n; i++){
        if (in[i] & 1) {st = i;break;}
    }
    dfs(st);
    for (int i = 0; i < (int)path.size(); i++) printf("%d ", path[i]);
    puts("");
    return 0;
}

例题，【例题】一笔画问题

//寻找欧拉路/欧拉回路。
//找到入度是奇数的点，这个点作为出发点。否则就从1开始出发
//dfs()遍历图，一边走一遍划掉边

例题，铲雪车(snow)

//每条道路都是双向道路，题面说明可以遍历所有街道，那一定是欧拉回路的
//直接利用欧拉回路的性质解题
//需要注意的是时间有可能很大，不开LL见祖宗

例题，骑马修栅栏(fence)

//一笔画问题，一笔遍历完所有栅栏
//完成建图后，从度数是奇数的点出发，进行dfs()，一边走一边抹掉边
//题目中没有给出结点编号范围，在读入的时候，明确一下起始和终止结点编号

Hamiltonian paths哈密尔顿路径

A Hamiltonian path is a path that visits each node of the graph exactly once. For example, the graph contains a Hamiltonian path from node 1 to node 3:

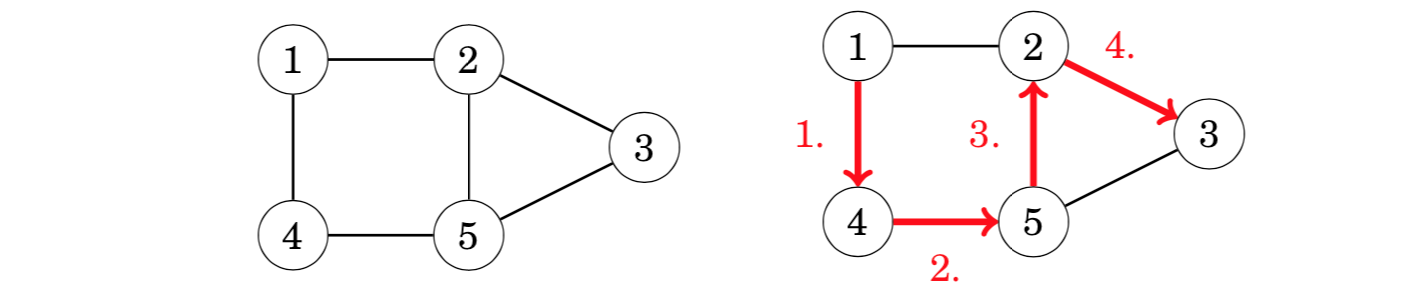
If a Hamiltonian path begins and ends at the same node, it is called a Hamiltonian circuit. The graph above also has an Hamiltonian circuit that begins and ends at node 1:

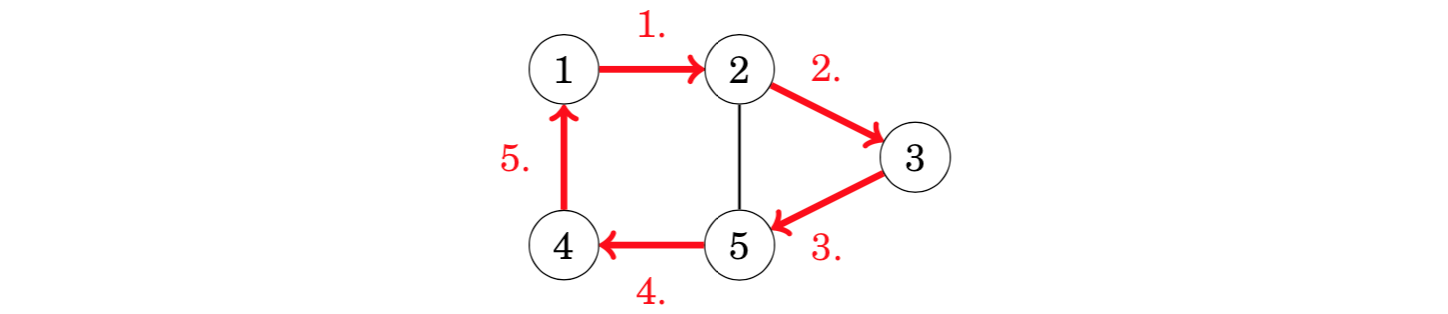
Construction

Since there is no efficient way to check if a Hamiltonian path exists, it is clear that there is also no method to efficiently construct the path, because otherwise we could just try to construct the path and see whether it exists.

A simple way to search for a Hamiltonian path is to use a backtracking algorithm that goes through all possible ways to construct the path. The time complexity of such an algorithm is at least , because there are different ways to choose the order of n nodes.(使用complete search + backtracking直接搜)

A more efficient solution is based on dynamic programming . The idea is to calculate values of a function possible (S, x), where S is a subset of nodes and x is one of the nodes. The function indicates whether there is a Hamiltonian path that visits the nodes of S and ends at node x. It is possible to implement this solution in .(使用状压dp)

例题，最短Hamilton路径

//求起点0到终点n-1的最短Hamilton路径
//使用了状压dp
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
int dp[1 << N][N], a[N][N], n;
int main(){
    cin >> n;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            cin >> a[i][j];
    memset(dp, 0x3f, sizeof dp);
    dp[1][0] = 0;  // 起点位置
    for (int mask = 1; mask < (1 << n); mask++)
        for (int end = 0; end < n; end++)    
            if (mask >> end & 1)    // 走过end
                for (int from = 0; from < n; from++){
                    // hamilton路径要求，到达from结点的状态中，不能经过end这个结点,
                    // 所以要把end这个点异或掉。从而，才能实现从from转移到end
                    if ((mask ^ (1 << end)) >> from & 1)  
                        dp[mask][end] = min(dp[mask][end],
                                            dp[mask ^ (1 << end)][from] + a[from][end]);
                }
    cout << dp[(1 << n) - 1][n - 1] << '\n';
    return 0;
}
/*
填表法 ：就是一般的动态规划，当前点的状态，可以直接用状态方程，根据之前点的状态推导出来。
刷表法：由当前点的状态，更新其他点的状态。需要注意：只用当每个状态所依赖的状态对它的影响相互独立。
上面那个是填表法
下面这个是刷表法
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
int dp[1 << N][N], a[N][N], n;
int main(){
    cin >> n;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            cin >> a[i][j];
    memset(dp, 0x3f, sizeof dp);
    dp[1][0] = 0;  // 起点位置
    for (int mask = 1; mask < (1 << n); mask++)
        for (int end = 0; end < n; end++)    
            if (mask >> end & 1)    // 走过end
                for (int nxt = 0; nxt < n; nxt++)
                    if (!(mask >> nxt & 1))
                        dp[mask | (1 << nxt)][nxt] = min(
                                dp[mask | (1 << nxt)][nxt],
                                dp[mask][end] + a[end][nxt]
                        );
    cout << dp[(1 << n) - 1][n - 1] << '\n';
    return 0;
}

大纲要求

•【4】图的深度优先遍历算法

•【4】图的宽度优先遍历算法

•【5】洪水填充算法（floodfill）