概念

学习使用递归的前提： 函数理解深入（带参的函数，有返回值的函数，函数的嵌套(就是“自身调用自身”)） 操作时，试验无限递归 递归的终止条件 “回溯时还原现场”保证执行前后程序面对问题的状态是相同的。

递归是程序遍历状态空间的基本方式。
以“原问题”为起点，尝试寻找把状态空间缩小到已知的“问题边界”的路线。
再通过该路线反向回溯的遍历方式，就是递归。

程序在每个步骤应该面对相同种类的问题，这些问题都是原问题的一个子问题，可能仅在规模或者某些限制条件上有所区别，并且能够使用“求解原问题的程序”进行求解。程序在执行变换操作执行三个操作：

  1. 缩小问题状态空间的规模。程序尝试寻找在 “原问题” 与 “问题边界” 之间的变换路线，并向正在探索的路线上迈进一步。
  2. 尝试求解规模缩小以后的问题，可能成功，可能失败。
  3. 如果成功，即找到了规模缩小后的问题的答案，那么将答案扩展到当前问题。如果失败，那么重新回到当前问题，程序可能会继续寻找当前问题的其他变换路线，直到最终确定当前问题无法求解。

在使用枚举算法蛮力搜索问题的整个“状态空间”时，经常需要递归。
枚举算法，就是遍历一遍，逐个举例。
初级的枚举很简单，就是for循环的应用，高级的就很难了，复杂在题目理解和遍历的操作方式

Thinking recursively is natural, but need good amount of training.

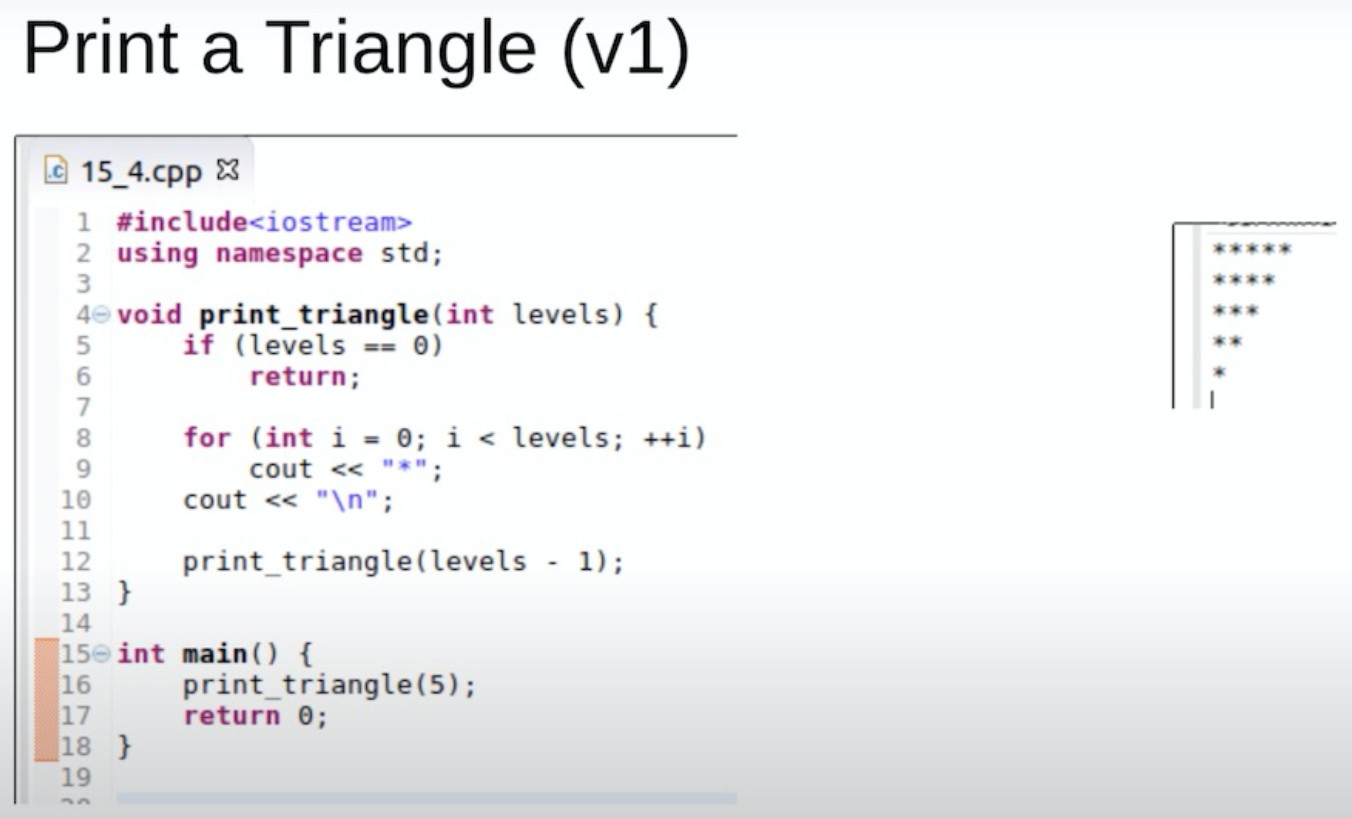
image.png

  1. void TriangleRev(int x) {
  2.    if (x <= 0) return;
  4.    for (int i = 1; i <= x; i++)
  5.         cout << "*";
  7.     cout << endl;
  9.     TriangleRev(x - 1);
  10. }
  12. /*
  13. Call TriangleRev(7)
  14. TriangleRev(7) <-- prints 7 stars & new line
  15.   TriangleRev(6) <-- prints 6 stars & new line
  16.     TriangleRev(5) <-- prints 5 stars & new line
  17.       TriangleRev(4) <-- prints 4 stars & new line
  18.         TriangleRev(3) <-- prints 3 stars & new line
  19.           TriangleRev(2) <-- prints 2 stars & new line
  20.             TriangleRev(1) <-- prints 1 star & new line
  21.               TriangleRev(0) <-- base case
  22.             TriangleRev(1)
  23.           TriangleRev(2)
  24.         TriangleRev(3)
  25.       TriangleRev(4)
  26.     TriangleRev(5)
  27.   TriangleRev(6)
  28. TriangleRev(7)
  30. The output will be:
  31. *******
  32. ******
  33. *****
  34. ****
  35. ***
  36. **
  37. *
  39. */

image.png

  1. void Triangle(int x) {
  2.    if (x <= 0) return;
  4.    Triangle(x - 1);
  6.    for (int i = 1; i <= x; i++)
  7.         cout << "*";
  8.    cout << endl;
  9. }
  12. /*
  13. Call Triangle(7)
  14. Triangle(7)
  15.   Triangle(6)
  16.     Triangle(5)
  17.       Triangle(4)
  18.         Triangle(3)
  19.           Triangle(2)
  20.             Triangle(1)
  21.               Triangle(0) <-- base case
  22.             Triangle(1) <-- prints 1 star & new line
  23.           Triangle(2) <-- prints 2 stars & new line
  24.         Triangle(3) <-- prints 3 stars & new line
  25.       Triangle(4) <-- prints 4 stars & new line
  26.     Triangle(5) <-- prints 5 stars & new line
  27.   Triangle(6) <-- prints 6 stars & new line
  28. Triangle(7) <-- prints 7 stars & new line
  30. The output will be:
  32. *
  33. **
  34. ***
  35. ****
  36. *****
  37. ******
  38. *******
  39. */

How to trace recursion

  1. // Factorial(n) = n * Factorial(n-1).        
  2. // Factorial(0) = Factorial(1) = 1
  4. int Fact(int n)
  5. {
  6.     if(n <= 1)
  7.         return 1;
  9.     return n * Fact(n-1);
  10. }
  12. /*
  13. Fact(4)
  14.     4* Fact(3)
  15.         3* Fact(2)
  16.             2* Fact(1)
  17.             2* 1 <-- 2
  18.         3* 2 <-- 6
  19.     4* 6 <-- 24
  20. */
  1. void printNumber(int n)    // for n > 0
  2. {    // 1234567
  3.     if(n)
  4.     {
  5.         printNumber(n/10);  // 214/10 = 21
  6.         cout<<n%10;         // 214%10 = 4
  7.     }
  8. }
  10. // E.g. 7 = 111        214 = 11010110
  11. // If number%2 get for us last bit in binray representation
  12. // If we could print last bit, we could print
  13. void printNumberBits(int n)    // for n > 0
  14. {
  15.     if(n)
  16.     {
  17.         printNumberBits(n/2);    // 214/2 = 1101011  last bit removed
  18.         cout<<n%2;              // 214%2 = 0
  19.     }
  20. }

入门例题

爬楼梯
  1. // 理解推导公式后，利用递归实现

菲波那契数列
  1. // 理解推导公式后，利用递归实现

Pell数列
  1. // 需要使用记忆化