本章面向区间动态规划展开
题目是从ACM训练内容上选用的,题面英文,内容较难
一本通上有几道区间dp的习题,模型比较类似,可以作为入门题
所谓区间问题,就是给出的问题是按区间的性质进行的,要么合并,要么分解为区间操作。《CCF中学生计算机程序设计》
区间DP的主要思想是先在小区间进行DP得到最优解,然后再利用小区间的最优解合并求大区间的最优解。《算法竞赛入门到进阶》
区间DP也属于线性DP中的一种,它以“区间长度”作为DP的“阶段”,使用两个坐标(区间的左、右端点)描述每个维度。在区间DP中,一个状态由若干个比它更小且包含于它的区间所代表的状态转移而来,因此,区间DP的决策往往就是划分区间的方法。区间DP的初态,一般由长度为1的“元区间”构成。这种向下划分、再向上递推的模式与某些树形结构,有很大的相似之处。《算法竞赛进阶指南》
区间类动态规划是线性动态规划的扩展,它在分阶段地划分问题时,与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。
令状态 f[i, j] 表示将下标位置 i 到 j 的所有元素合并能获得的价值的最大值,那么f[i, j] = max{f(i, k) + f(k + 1, j) + cost}
Nested Ranges Style(((a)(bc))(def))(ghijkl)Consecutive Ranges Style(ab)(cde)(fg)General Ranges Style回文串
Nested Ranges Style
例题,合并石子
在一个操场上一排地摆放着N堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆石子合并成新的一堆,并将新的一堆石子数记为该次合并的得分。计算出将N堆石子合并成一堆的最小得分。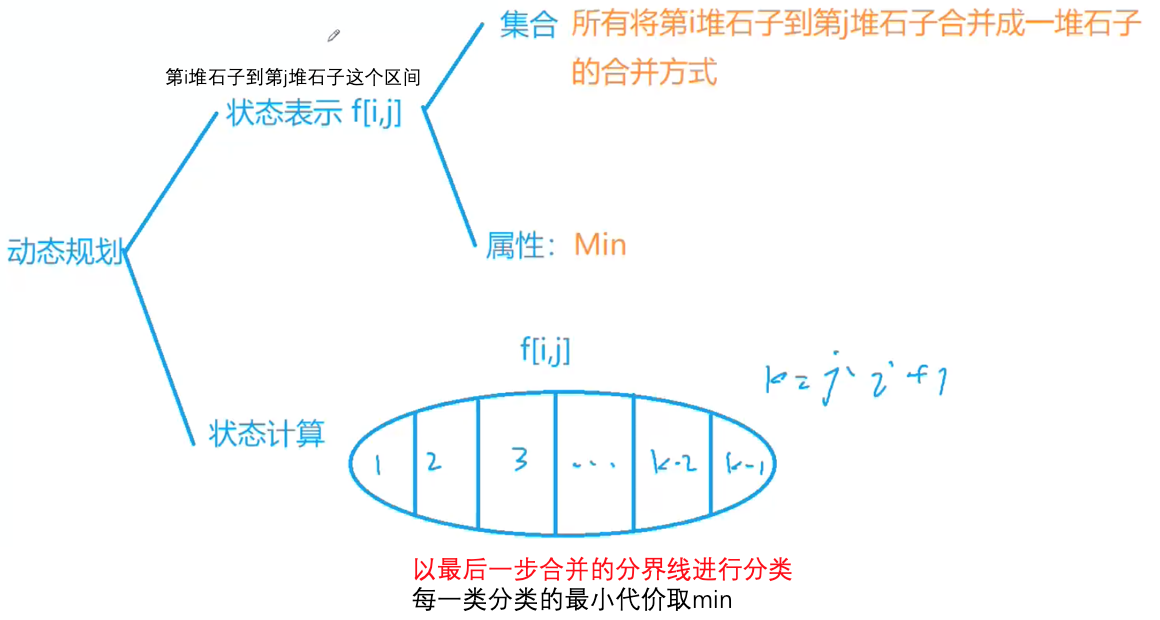

例题,【例9.18】合并石子
#include <bits/stdc++.h>using namespace std;const int N = 310;int a[N], s[N], n;int f[N][N]; // f[i][j]表示合并[i,j]区间的石子需要耗费的体力int main(){cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];s[i] = s[i - 1] + a[i];}memset(f, 0x3f, sizeof f);for (int i = 1; i <= n; i++) f[i][i] = 0; // 自己一个的时候,不用合并,耗费是0for (int len = 2; len <= n; len++) // 阶段,有两个石子才发生合并的行为for (int i = 1; i <= n - len + 1; i++){ // 状态 左端点iint j = i + len - 1; // 状态 右端点jfor (int k = i; k < j; k++)f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j]);f[i][j] += s[j] - s[i - 1];}cout << f[1][n] << '\n';return 0;}
例题,CasketOfStar



// my_code, cannot submit to Topcoder#include <bits/stdc++.h>using namespace std;const int N = 55;int weight[N], mem[N][N];int n;int best(int i, int j){if (j - i + 1 <= 2) return 0;if (j - i + 1 == 3) return weight[i] * weight[j];int &ret = mem[i][j];if (ret != -1) return ret;for (int k = i + 1; k < j; k++)ret = max(ret, best(i, k) + best(k, j) + weight[i] * weight[j]);return ret;}int main(){cin >> n;for (int i = 1; i <= n; i++) cin >> weight[i];memset(mem, -1, sizeof mem);cout << best(1, n) << '\n';return 0;}
例题,Cutting Sticks

// Cutting Sticks,请上机练习// 代码比较类似
例题,Optimal Array Multiplication Sequence

// 难度:提高+/省选-// 需要递归输出方案// 请上机操作,课后自行展开,提高代码能力
Consecutive Ranges Style
例题,Pearls
#include <bits/stdc++.h>using namespace std;const int N = 110, INF = 0x3f3f3f3f;int a[N], p[N], n, T;int mem[N][N];int best(int u, int last){if (u == n + 1) return 0;int &ret = mem[u][last];if (ret != INF) return ret;int sum = 10;for (int i = last; i <= u; i++) sum += a[i];//buy now, add to right now intervalret = min(ret, sum * p[u] + best(u + 1, u + 1));if (u != n) ret = min(ret, best(u + 1, last));return ret;}int main(){cin >> T;while (T--){cin >> n;for (int i = 1; i <= n; i++) cin >> a[i] >> p[i];memset(mem, 0x3f, sizeof mem);printf("%d\n", best(1, 1));}return 0;}
#include <bits/stdc++.h>using namespace std;const int N = 110, INF = 0x3f3f3f3f;int a[N], p[N], n, T;int mem[N][N];int s[N];int best(int u, int last){if (u == n + 1) return 0;int &ret = mem[u][last];if (ret != INF) return ret;int sum = 10 + s[u] - s[last - 1];//buy now, add to right now intervalret = min(ret, sum * p[u] + best(u + 1, u + 1));if (u != n) ret = min(ret, best(u + 1, last));return ret;}int main(){cin >> T;while (T--){cin >> n;for (int i = 1; i <= n; i++) cin >> a[i] >> p[i];memset(s, 0, sizeof s);for (int i = 1; i <= n; i++) s[i] += s[i - 1] + a[i];memset(mem, 0x3f, sizeof mem);printf("%d\n", best(1, 1));}return 0;}
#include <bits/stdc++.h>using namespace std;const int N = 110, INF = 0x3f3f3f3f;int a[N], p[N], n, T, s[N];int dp[N];int main(){cin >> T;while (T--){memset(s, 0, sizeof s);memset(dp, 0x3f, sizeof dp);cin >> n;for (int i = 1; i <= n; i++) cin >> a[i] >> p[i];for (int i = 1; i <= n; i++) s[i] += s[i - 1] + a[i];dp[0] = 0;for (int i = 1; i <= n; i++)for (int j = 1; j <= i; j++)dp[i] = min(dp[i], dp[j - 1] + (s[i] - s[j - 1] + 10) * p[i]);cout << dp[n] << '\n';}return 0;}
General Ranges Style
例题,String to Palindrome

// 递归写法,my 10739_1.cpp# include<vector># include<string># include<iostream>using namespace std;string A, B;const int MAX = 1000+9;int memo[MAX][MAX];int best(int i, int j){if(i >= j)return 0;int &ret = memo[i][j];if(ret != -1)return ret;ret = best(i+1, j-1) + (A[i] != A[j]);ret = min(ret, best(i+1, j)+1);ret = min(ret, best(i, j-1)+1);return ret;}int main() {int num;cin >> num;for (int i = 1; i <= num; i++) {cin >> A;memset(memo, -1, sizeof memo);cout << "Case " << i << ": " << best(0, (int)A.size()-1) << endl;}return 0;}
// 循环写法#include<iostream>#include<string>using namespace std;int min(int a, int b, int c){if(b < a) a = b;if(c < a) a = c;return a;}int A[1001][1001]; /* The cost of substring A[i][j] */int main(){int i, j, k, len, cases, diag;string str;cin>>cases;for (k = 1; k <= cases; k++){cin>>str;for (i=0; i<str.size(); i++) /* Base case in diagonal */A[i][i] = 0; /* Empty string */for (len = 2; len <= str.size(); len++) /* O(n^2) */{ /* when len = 2 --> Special case */for (i = 0; i+len<=str.size(); i++){j = i + len - 1, diag = 0;if (str[i] != str[j])diag = 1;if( i+1 <= j-1 ) /* at least j-i > 1 */A[i][j] = min(A[i+1][j]+1, A[i][j-1]+1, A[i+1][j-1]+diag);else /* Undefined Stage (Not in base case) i = j+1 */A[i][j] = diag; /* j=i+1Tow char string */}}cout<<"Case "<<k<<": "<<A[0][str.size()-1]<< "\n";}return 0;}// by zqiceberg#include <bits/stdc++.h>using namespace std;const int N = 1010;int T, idx;int dp[N][N];char s[N];int main(){cin >> T;while (T--){scanf("%s", s);int LEN = strlen(s);for (int i = 0; i < LEN; i++) dp[i][i] = 0;for (int len = 2; len <= LEN; len++)for (int i = 0; i + len <= LEN; i++){int j = i + len - 1;int flag = 0;if (s[i] != s[j]) flag = 1;if (i + 1 <= j - 1){dp[i][j] = dp[i + 1][j - 1] + flag;dp[i][j] = min(dp[i][j], dp[i + 1][j] + 1);dp[i][j] = min(dp[i][j], dp[i][j - 1] + 1);}else dp[i][j] = flag;}printf("Case %d: %d\n", ++idx, dp[0][LEN - 1]);}return 0;}
例题,Cheapest Palindrome
#include <iostream>#include <cstdio>using namespace std;const int N = 2010;char s[N];int w[N], dp[N][N]; // dp[i][j]表示 子区间[i...j]变成回文的最小花费int n, m;int main(){cin >> n >> m;scanf("%s", s);for (int i = 0; i < n; i++){char c;int x, y;cin >> c >> x >> y;w[c - 'a'] = min(x, y);}// 枚举的区间是从小区间扩展到大区间for (int i = m - 1; i >= 0; i--)for (int j = i + 1; j < m; j++){if (s[i] == s[j]){dp[i][j] = dp[i + 1][j - 1];}else{dp[i][j] = min(dp[i + 1][j] + w[s[i] - 'a'],dp[i][j - 1] + w[s[j] - 'a']);}}cout << dp[0][m - 1] << '\n';return 0;}
例题,【例9.20】编辑距离
//Tips: 对比一下最短编辑距离
例题代码
// 例题,Cutting Sticks#include <bits/stdc++.h>using namespace std;const int N = 55;int a[N], l, n;int mem[N][N];int best(int i, int j){if (j - i <= 1) return 0;if (j - i == 2) return a[j] - a[i];int &ret = mem[i][j];if (ret != 0x3f3f3f3f) return ret;for (int k = i + 1; k < j; k++){ret = min(ret, best(i, k) + best(k, j) + a[j] - a[i]);}return ret;}int main(){while (cin >> l){if (l == 0) break;cin >> n;for (int i = 1; i <= n; i++) scanf("%d", &a[i]);a[0] = 0, a[n + 1] = l;memset(mem, 0x3f, sizeof mem);printf("The minimum cutting is %d.\n", best(0, n + 1));}return 0;}
// 例题,Optimal Array Multiplication Sequence#include <bits/stdc++.h>using namespace std;typedef pair<int, int> PII;const int N = 20, INF = 0x3f3f3f3f;PII a[N];int path[N][N];int n, idx;int mem[N][N];void print(int i, int j){if (j == i){printf("A%d", i);return ;}if (j - i == 1){printf("(A%d x A%d)", i, j);return ;}int k = path[i][j];printf("(");print(i, k);printf(" x ");print(k + 1, j);printf(")");}int best(int i, int j){if (j - i == 0) return 0;if (j - i == 1) return mem[i][j] = a[i].first * a[i].second * a[j].second;if (mem[i][j] != INF) return mem[i][j];int &ret = mem[i][j];for (int k = i; k < j; k++){int t = best(i, k) + best(k + 1, j) + a[i].first * a[k].second * a[j].second;if (t < ret){ret = t;path[i][j] = k;}}return ret;}int main(){while (cin >> n && n){idx++;for (int i = 1; i <= n; i++){cin >> a[i].first >> a[i].second;}memset(mem, 0x3f, sizeof mem);best(1, n);printf("Case %d: ", idx);print(1, n);puts("");}return 0;}

