DP Illustration

例题，Wedding shopping UVA-11450

// 先读题

Complete Search(TLE)

Top-Down DP(AC)

#include <bits/stdc++.h>
using namespace std;
int T, M, C;
int price[25][25];
int memo[25][210];
int shop(int u, int remain){
    if (remain < 0) return -1;
    if (u == C) return M - remain;
    int &ret = memo[u][remain];
    if (ret != -1) return ret;
    for (int model = 1; model <= price[u][0]; model++)
        ret = max(ret, shop(u + 1, remain - price[u][model]));
    return ret;
}
int main(){
    cin >> T;
    while (T--){
        cin >> M >> C;
        for (int i = 0; i < C; i++){
            cin >> price[i][0];  // 个数
            for (int j = 1; j <= price[i][0]; j++) cin >> price[i][j];
        }
        memset(memo, -1, sizeof memo);
        int ret = shop(0, M);
        if (ret < 0) cout << "no solution" << '\n';
        else cout << ret << '\n';
    }
    return 0;
}

Bottom-Up DP(AC)

#include <bits/stdc++.h>
using namespace std;
int T, M, C;
int price[25][25];
bool reachable[25][210];
int main(){
    cin >> T;
    while (T--){
        cin >> M >> C;
        for (int i = 0; i < C; i++){
            cin >> price[i][0];
            for (int j = 1; j <= price[i][0]; j++)
                cin >> price[i][j];
        }
        memset(reachable, false, sizeof reachable);
        // base cases
        for (int j = 1; j <= price[0][0]; j++)
            if (M - price[0][j] >= 0) reachable[0][M - price[0][j]] = true;
        for (int i = 1; i < C; i++)
            for (int money = 0; money < M; money++)
                if (reachable[i - 1][money]){                // 第i-1层的剩余money是可达的
                    for (int j = 1; j <= price[i][0]; j++)
                        if (money >= price[i][j])            // 剩余money够买第j个物品的
                            reachable[i][money - price[i][j]] = true;
                }
        int money = 0;
        while (money <= M && !reachable[C - 1][money]) money++;
        if (money == M + 1) cout << "no solution" << '\n';
        else cout << M - money << '\n';
    }
    return 0;
}

// 利用滚动数组优化
#include <bits/stdc++.h>
using namespace std;
int T, M, C;
int price[25][25];
bool reachable[2][210];
int main(){
    cin >> T;
    while (T--){
        cin >> M >> C;
        for (int i = 0; i < C; i++){
            cin >> price[i][0];
            for (int j = 1; j <= price[i][0]; j++)
                cin >> price[i][j];
        }
        memset(reachable, false, sizeof reachable);
        // base cases
        for (int j = 1; j <= price[0][0]; j++)
            if (M - price[0][j] >= 0) reachable[0 & 1][M - price[0][j]] = true;
        for (int i = 1; i < C; i++){
            // 当前第i层的可达状态清空一下，避免和之前的混用
            memset(reachable[i & 1], false, sizeof reachable[i & 1]);  
            for (int money = 0; money < M; money++)
                if (reachable[(i - 1) & 1][money]){                // 第i-1层的剩余money是可达的
                    for (int j = 1; j <= price[i][0]; j++)
                        if (money >= price[i][j]){                // 剩余money够买第j个物品的
                            reachable[i & 1][money - price[i][j]] = true;
                        }
                }
        }
        int money = 0;
        while (money <= M && !reachable[(C - 1) & 1][money]) money++;
        if (money == M + 1) cout << "no solution" << '\n';
        else cout << M - money << '\n';
    }
    return 0;
}
// Note that for this problem, the memory savings are not significant. 
// For harder DP problems, 
// for example where there might be thousands of garment models instead of 20, 
// this space saving trick can be important.

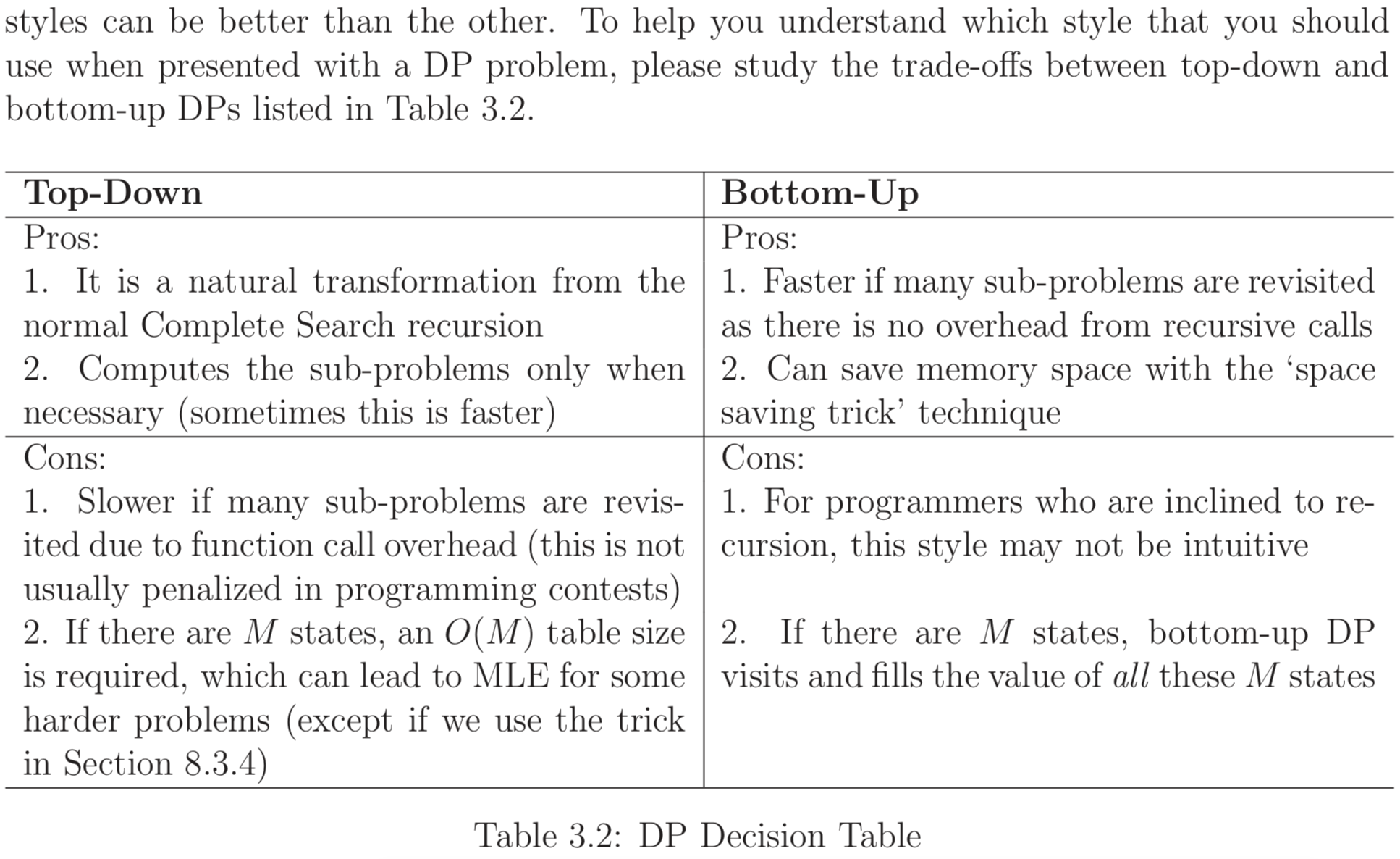
Top-Down verus Bottom-Up Dp

Displaying the Optimal Solution

#include <bits/stdc++.h>
using namespace std;
int T, M, C;
int price[25][25];
int memo[25][210];
int shop(int u, int remain){
    if (remain < 0) return -1;
    if (u == C) return M - remain;
    int &ret = memo[u][remain];
    if (ret != -1) return ret;
    for (int model = 1; model <= price[u][0]; model++)
        ret = max(ret, shop(u + 1, remain - price[u][model]));
    return ret;
}
void print_shop(int u, int remain){
    if (remain < 0 || u == C) return ;
    for (int model = 1; model <= price[u][0]; model++){
        if (shop(u + 1, remain - price[u][model]) == memo[u][remain]){
            printf("%d%c", price[u][model], u == C  - 1 ? '\n' : ' ');
            print_shop(u + 1, remain - price[u][model]);
            break;
        }
    }
}
int main(){
    cin >> T;
    while (T--){
        cin >> M >> C;
        for (int i = 0; i < C; i++){
            cin >> price[i][0];  // 个数
            for (int j = 1; j <= price[i][0]; j++) cin >> price[i][j];
        }
        memset(memo, -1, sizeof memo);
        int ret = shop(0, M);
        if (ret < 0) cout << "no solution" << '\n';
        else cout << ret << '\n';
        print_shop(0, M);
    }
    return 0;
}

Remarks Aboubt Dynamic Programming in Programming Contests