本章，主要是面向记忆化展开
递归+记忆化，是非常实用的方法， 尤其是刚进入普及组算法阶段，递归还是比较好想，好写的
本讲介绍一些关于套路的东西， 对于套路，套路的用法是：先走进去，再走出来
和三四年级刚开始写作文的时候，感觉类似，都是模仿套路 到了五六年级，有能力写一些郊游游记，表达一些自己的想法


本章中的内容，大多已经学习过 材料中给出的示例代码并不是推荐的代码风格和写法 目的在于锻炼大家阅读一下的能力，别看了别人代码就看不懂的白学地步 同时，也给大家开阔视野，成人的代码，风格就大概类似了，也并不代码谁好谁坏 适合当下的自己，就是最好的，兼容并包更优美的写法，是比较靠谱的 也不可执着于自己的见识，敢于尝试新的事物，多吸纳新的事物

动态规划解题核心框架

动态规划是什么？解决动态规划问题有什么技巧？如何学习动态规划？

首先，动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列，最小编辑距离等等（动态规划问题的场景，有三种：求最大值，求最小值，求方案数）。

既然是要求最值，核心问题是什么呢？求解动态规划的核心问题是穷举。因为要求最值，肯定要把所有可行的答案穷举出来，然后在其中找最值。

动态规划这么简单，就是穷举就完事了？我们看到的动态规划问题都很难啊！

首先，动态规划的穷举有点特别，因为这类问题存在“重叠子问题”，
如果暴力穷举的话效率会极其低下，所以需要记忆数组来优化穷举过程，避免不必要的计算。

而且，动态规划问题一定会具备“最优子结构”，才能通过子问题的最值得到原问题的最值。

另外，虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，只有列出正确的“状态转移方程”，才能正确地穷举。

以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。在实际的算法问题中，写出状态转移方程是最困难的(我感觉，状态的设计，才是第一难)，这也就是为什么很多朋友觉得动态规划问题困难的原因，我来提供我研究出来的一个思维框架，辅助你思考状态转移方程：

  1. 明确 base case 
  2. |
  3. |
  4. v
  5. 明确「状态」
  6. |
  7. |
  8. v
  9. 明确「选择」
  10. |
  11. |
  12. v 
  13. 定义 dp 数组/函数的含义

按上面的套路走，最后的结果就可以套这个框架：

  1. # 初始化 base case
  2. dp[0][0][...] = base
  4. # 进行状态转移
  5. for 状态1 in 状态1的所有取值：
  6.     for 状态2 in 状态2的所有取值：
  7.         for ...
  8.             dp[状态1][状态2][...] = 求最值(选择1，选择2...)

下面通过斐波那契数列问题和凑零钱问题来详解动态规划的基本原理。
前者主要是让你明白什么是重叠子问题（斐波那契数列没有求最值，所以严格来说不是动态规划问题）
后者主要举集中于如何列出状态转移方程。

斐波那契数列

只有简单的例子才能让你把精力充分集中在算法背后的通用思想和技巧上，而不会被那些隐晦的细节问题搞的莫名其妙。

1、暴力递归

  1. // 斐波那契数列的数学形式就是递归的，写成代码就是这样：
  2. int fib(int N) {
  3.     if (N == 1 || N == 2) return 1;
  4.     return fib(N - 1) + fib(N - 2);
  5. }

我们也知道这样写代码虽然简洁易懂，但是十分低效，低效在哪里？假设 n = 20，请画出递归树：
image.png

PS：但凡遇到需要递归的问题，最好都画出递归树，这对你分析算法的复杂度，寻找算法低效的原因都有巨大帮助。

这个递归树怎么理解？就是说想要计算原问题 f(20)，我就得先计算出子问题 f(19) 和 f(18)，然后要计算 f(19)，我就要先算出子问题 f(18) 和 f(17)，以此类推。最后遇到 f(1) 或者 f(2) 的时候，结果已知，就能直接返回结果，递归树不再向下生长了。

递归算法的时间复杂度怎么计算？就是用子问题个数乘以解决一个子问题需要的时间。

首先计算子问题个数，即递归树中节点的总数。显然二叉树节点总数为指数级别，所以子问题个数为 O(2^n)。

然后计算解决一个子问题的时间，在本算法中，没有循环，只有 f(n - 1) + f(n - 2) 一个加法操作，时间为 O(1)。

所以，这个算法的时间复杂度为二者相乘，即 O(2^n)，指数级别，爆炸。

观察递归树，很明显发现了算法低效的原因：存在大量重复计算，比如 f(18) 被计算了两次，而且你可以看到，以 f(18) 为根的这个递归树体量巨大，多算一遍，会耗费巨大的时间。更何况，还不止 f(18) 这一个节点被重复计算，所以这个算法及其低效。

这就是动态规划问题的第一个性质：重叠子问题。下面，我们想办法解决这个问题。

2、带备忘录的递归解法(记忆化)

明确了问题，其实就已经把问题解决了一半。即然耗时的原因是重复计算，那么我们可以造一个「备忘录」，每次算出某个子问题的答案后别急着返回，先记到「备忘录」里再返回；每次遇到一个子问题先去「备忘录」里查一查，如果发现之前已经解决过这个问题了，直接把答案拿出来用，不要再耗时去计算了。

一般使用一个数组充当这个「备忘录」，当然你也可以使用哈希表（字典），思想都是一样的。

  1. public int fib(int N) {
  2.     // 备忘录全初始化为 0
  3.     int[] memo = new int[N + 1];
  4.     // 进行带备忘录的递归
  5.     return helper(memo, N);
  6. }
  8. private int helper(int[] memo, int n) {
  9.     // base case
  10.     if (n == 0 || n == 1) return n;
  11.     // 已经计算过，不用再计算了
  12.     if (memo[n] != 0) return memo[n];
  13.     memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
  14.     return memo[n];
  15. }
  17. // 这个代码示例，代码风格和现在的，不是很一样
  18. // 这个代码是一个工作后的人写的，写给成人教学的代码
  19. // 风格是这样，我认为，这里面有很多多余

现在，画出递归树，你就知道「备忘录」到底做了什么。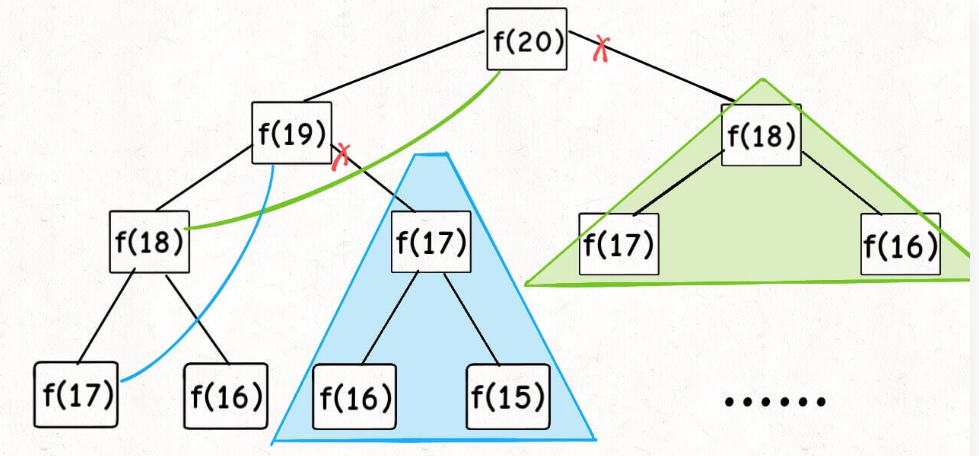
image.png

实际上，带「备忘录」的递归算法，把一棵存在巨量冗余的递归树通过「剪枝」，改造成了一幅不存在冗余的递归图，极大减少了子问题（即递归图中节点）的个数。
image.png

递归算法的时间复杂度怎么计算？就是用子问题个数乘以解决一个子问题需要的时间。

子问题个数，即图中节点的总数，由于本算法不存在冗余计算，子问题就是 f(1), f(2), f(3) … f(20)，数量和输入规模 n = 20 成正比，所以子问题个数为 O(n)。

解决一个子问题的时间，同上，没有什么循环，时间为 O(1)。

所以，本算法的时间复杂度是 O(n)。比起暴力算法，是降维打击。

至此，带备忘录的递归解法的效率已经和迭代的动态规划解法一样了。实际上，这种解法和迭代的动态规划已经差不多了，只不过这种方法叫做「自顶向下」，动态规划叫做「自底向上」。

啥叫「自顶向下」？注意我们刚才画的递归树（或者说图），是从上向下延伸，都是从一个规模较大的原问题比如说 f(20)，向下逐渐分解规模，直到 f(1) 和 f(2) 这两个 base case，然后逐层返回答案，这就叫「自顶向下」。

啥叫「自底向上」？反过来，我们直接从最底下，最简单，问题规模最小的 f(1) 和 f(2) 开始往上推，直到推到我们想要的答案 f(20)，这就是动态规划的思路，这也是为什么动态规划一般都脱离了递归，而是由循环迭代完成计算。

3、DP数组的循环写法

有了上一步「备忘录」的启发，我们可以把这个「备忘录」独立出来成为一张表，就叫做 DP table 吧，在这张表上完成「自底向上」的推算岂不美哉！（DP table就是我们常说的状态表示）

  1. public int fib(int N) {
  2.     if (N == 0) return 0;
  3.     int[] dp = new int[N + 1];
  4.     // base case
  5.     dp[0] = 0; dp[1] = 1;
  6.     // 状态转移
  7.     for (int i = 2; i <= N; i++) {
  8.         dp[i] = dp[i - 1] + dp[i - 2];
  9.     }
  11.     return dp[N];
  12. }

image.png

画个图就很好理解了，而且你发现这个 DP table 特别像之前那个「剪枝」后的结果，只是反过来算而已。实际上，带备忘录的递归解法中的「备忘录」，最终完成后就是这个 DP table，所以说这两种解法其实是差不多的，大部分情况下，效率也基本相同。

这里，引出「状态转移方程」这个名词，实际上就是描述问题结构的数学形式：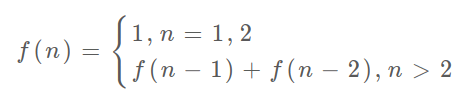
image.png
为啥叫「状态转移方程」？其实就是为了听起来高端。
你把 f(n) 想做一个状态 n，这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来，
这就叫状态转移，仅此而已。

你会发现，上面的几种解法中的所有操作，例如 return f(n - 1) + f(n - 2)，dp[i] = dp[i - 1] + dp[i - 2]，以及对备忘录或 DP table 的初始化操作，都是围绕这个方程式的不同表现形式。

可见列出「状态转移方程」的重要性，它是解决问题的核心。
而且很容易发现，其实状态转移方程直接代表着暴力解法。

千万不要看不起暴力解，
动态规划问题最困难的就是写出这个暴力解，即状态转移方程。
只要写出暴力解，优化方法无非是用备忘录或者 DP table，再无奥妙可言。

这个例子的最后，讲一个细节优化。
根据斐波那契数列的状态转移方程，当前状态只和之前的两个状态有关，
其实并不需要那么长的一个 DP table 来存储所有的状态，只要想办法存储之前的两个状态就行了。
所以，可以进一步优化，把空间复杂度降为 O(1)：

  1. // 这个代码就和我们学习循环的时候，写的代码一样了
  2. // 用三个变量迭代完成
  3. int fib(int n) {
  4.     if (n < 1) return 0;
  5.     if (n == 2 || n == 1) 
  6.         return 1;
  7.     int prev = 1, curr = 1;
  8.     for (int i = 3; i <= n; i++) {
  9.         int sum = prev + curr;
  10.         prev = curr;
  11.         curr = sum;
  12.     }
  13.     return curr;
  14. }

这个技巧就是所谓的「状态压缩」，如果我们发现每次状态转移只需要 DP table 中的一部分，那么可以尝试用状态压缩来缩小 DP table 的大小，只记录必要的数据

上述例子就相当于把DP table 的大小从 n 缩小到 2。后续的动态规划章节中我们还会看到这样的例子，一般来说是把一个二维的 DP table 压缩成一维，即把空间复杂度从 O(n^2) 压缩到 O(n)。

有人会问，动态规划的另一个重要特性「最优子结构」，怎么没有涉及？下面会涉及。斐波那契数列的例子严格来说不算动态规划，因为没有涉及求最值，以上旨在说明重叠子问题的消除方法，演示得到最优解法逐步求精的过程。下面，看第二个例子，凑零钱问题。

凑零钱问题, 第一部分

先看下题目：

  1. 给你 k 种面值的硬币，
  2. 面值分别为 c1, c2 ... ck，每种硬币的数量无限，
  3. 再给一个总金额 amount，
  4. 问你最少需要几枚硬币凑出这个金额，
  5. 如果不可能凑出，算法返回 -1 。

算法的函数声明(定义了函数的输入输出)如下：

  1. // coins 中是可选硬币面值，amount 是目标金额
  2. int coinChange(int[] coins, int amount);

比如说 k = 3，面值分别为 1，2，5，总金额 amount = 11。
那么最少需要 3 枚硬币凑出，即 11 = 5 + 5 + 1。

你认为计算机应该如何解决这个问题？显然，就是把所有可能的凑硬币方法都穷举出来，然后找找看最少需要多少枚硬币。

1、暴力递归

首先，这个问题是动态规划问题，因为它具有「最优子结构」的。
要符合「最优子结构」，子问题间必须互相独立。
啥叫相互独立？你肯定不想看数学证明，我用一个直观的例子来讲解。

比如说，假设你考试，每门科目的成绩都是互相独立的。你的原问题是考出最高的总成绩，那么你的子问题就是要把语文考到最高，数学考到最高…… 为了每门课考到最高，你要把每门课相应的选择题分数拿到最高，填空题分数拿到最高…… 当然，最终就是你每门课都是满分，这就是最高的总成绩。

得到了正确的结果：最高的总成绩就是总分。
因为这个过程符合最优子结构，“每门科目考到最高”这些子问题是互相独立，互不干扰的。

但是，如果加一个条件：你的语文成绩和数学成绩会互相制约，数学分数高，语文分数就会降低，反之亦然。这样的话，显然你能考到的最高总成绩就达不到总分了，按刚才那个思路就会得到错误的结果。因为子问题并不独立，语文数学成绩无法同时最优，所以最优子结构被破坏。

回到凑零钱问题，为什么说它符合最优子结构呢？
比如你想求 amount = 11 时的最少硬币数（原问题），
如果你知道凑出 amount = 10 的最少硬币数（子问题），
你只需要把子问题的答案加一（再选一枚面值为 1 的硬币）就是原问题的答案。
因为硬币的数量是没有限制的，所以子问题之间没有相互制，是互相独立的。

那么，既然知道了这是个动态规划问题，就要思考如何列出正确的状态转移方程？

1、确定 base case，这个很简单，显然目标金额 amount 为 0 时算法返回 0，因为不需要任何硬币就已经凑出目标金额了。

2、确定「状态」，也就是原问题和子问题中会变化的变量。由于硬币数量无限，硬币的面额也是题目给定的，只有目标金额会不断地向 base case 靠近，所以唯一的「状态」就是目标金额 amount。

3、确定「选择」，也就是导致「状态」产生变化的行为。目标金额为什么变化呢，因为你在选择硬币，你每选择一枚硬币，就相当于减少了目标金额。所以说所有硬币的面值，就是你的「选择」。

4、明确 dp 函数/数组的定义。我们这里讲的是自顶向下的解法，所以会有一个递归的 dp 函数，一般来说函数的参数就是状态转移中会变化的量，也就是上面说到的「状态」；函数的返回值就是题目要求我们计算的量。就本题来说，状态只有一个，即「目标金额」，题目要求我们计算凑出目标金额所需的最少硬币数量。

所以我们可以这样定义 dp 函数：
dp(n) 的定义：输入一个目标金额 n，返回凑出目标金额 n 的最少硬币数量。

搞清楚上面这几个关键点，解法的伪码就可以写出来了：

  1. // 伪码框架
  2. public int coinChange(int[] coins, int amount) {
  3.     // 题目要求的最终结果是 dp(amount)
  4.     return dp(coins, amount)
  5. }
  7. // 定义：要凑出金额 n，至少要 dp(coins, n) 个硬币
  8. int dp(int[] coins, int n) {
  9.     // 做选择，选择需要硬币最少的那个结果
  10.     for (int coin : coins) {
  11.         res = min(res, 1 + dp(n - coin))
  12.     }
  13.     return res
  14. }

根据伪码，我们加上 base case 即可得到最终的答案。显然目标金额为 0 时，所需硬币数量为 0；当目标金额小于 0 时，无解，返回 -1：

  1. // 示例代码写的比较繁琐，看下思路即可
  2. // 代码风格不推荐
  4. public int coinChange(int[] coins, int amount) {
  5.     // 题目要求的最终结果是 dp(amount)
  6.     return dp(coins, amount)
  7. }
  9. private int dp(int[] coins, int amount) {
  10.     // base case
  11.     if (amount == 0) return 0;
  12.     if (amount < 0) return -1;
  14.     int res = Integer.MAX_VALUE;
  15.     for (int coin : coins) {
  16.         // 计算子问题的结果
  17.         int subProblem = dp(coins, amount - coin);
  18.         // 子问题无解则跳过
  19.         if (subProblem == -1) continue;
  20.         // 在子问题中选择最优解，然后加一
  21.         res = Math.min(res, subProblem + 1);
  22.     }
  24.     return res == Integer.MAX_VALUE ? -1 : res;
  25. }
  1. // 扩展一下
  2. // 数组作为函数参数的写法
  3. #include <bits/stdc++.h>
  5. using namespace std;
  7. int a[] = {1, 2, 3, 4, 5, 6};
  8. int n = 6;
  10. int cal(int A[]){
  11.     int sum = 0;
  12.     for (int i = 0; i < n; i++) sum += A[i];
  13.     return sum;
  14. }
  16. int cal02(int *A){
  17.     int sum = 0;
  18.     for (int i = 0; i < n; i++) sum += *(A + i);
  19.     return sum;
  20. }
  22. int main(){
  23.     cout << cal02(a) << '\n';
  25.     return 0;
  26. }

至此，状态转移方程其实已经完成了，以上算法已经是暴力解法了，以上代码的数学形式就是状态转移方程：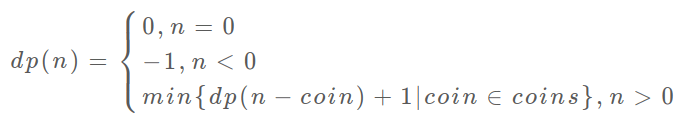
image.png

至此，这个问题其实就解决了，只不过需要消除一下重叠子问题，比如 amount = 11, coins = {1,2,5} 时画出递归树看看：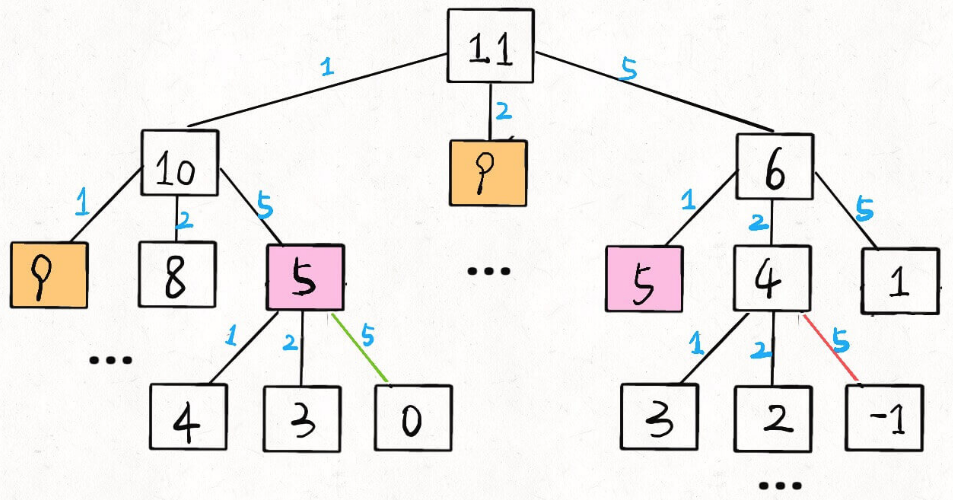
image.png

递归算法的时间复杂度分析：子问题总数 * 每个子问题的时间。

子问题总数为递归树节点个数，这个比较难看出来，是 O(n^k)，总之是指数级别的。
每个子问题中含有一个 for 循环，复杂度为 O(k)。所以总时间复杂度为 O(k * n^k)，指数级别。

2、带备忘录的递归解法(记忆化)

类似之前斐波那契数列的例子，只需要稍加修改，就可以通过备忘录消除子问题：

  1. int[] memo;
  3. public int coinChange(int[] coins, int amount) {
  4.     memo = new int[amount + 1];
  5.     // dp 数组全都初始化为特殊值
  6.     Arrays.fill(memo, -666);
  8.     return dp(coins, amount);
  9. }
  11. private int dp(int[] coins, int amount) {
  12.     if (amount == 0) return 0;
  13.     if (amount < 0) return -1;
  14.     // 查备忘录，防止重复计算
  15.     if (memo[amount] != -666)
  16.         return memo[amount];
  18.     int res = Integer.MAX_VALUE;
  19.     for (int coin : coins) {
  20.         // 计算子问题的结果
  21.         int subProblem = dp(coins, amount - coin);
  22.         // 子问题无解则跳过
  23.         if (subProblem == -1) continue;
  24.         // 在子问题中选择最优解，然后加一
  25.         res = Math.min(res, subProblem + 1);
  26.     }
  27.     // 把计算结果存入备忘录
  28.     memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res;
  29.     return memo[amount];
  30. }

不画图了，很显然「备忘录」大大减小了子问题数目，完全消除了子问题的冗余，所以子问题总数不会超过金额数 n，即子问题数目为 O(n)。处理一个子问题的时间不变，仍是 O(k)，所以总的时间复杂度是 O(kn)。

3、dp 数组的循环写法

当然，我们也可以自底向上使用 dp table 来消除重叠子问题，关于「状态」「选择」和 base case 与之前没有区别，dp 数组的定义和刚才 dp 函数类似，也是把「状态」，也就是目标金额作为变量。不过 dp 函数体现在函数参数，而 dp 数组体现在数组索引：

dp 数组的定义：当目标金额为 i 时，至少需要 dp[i] 枚硬币凑出。

根据我们文章开头给出的动态规划代码框架可以写出如下解法：

  1. // 写法繁琐，看下思路
  3. public int coinChange(int[] coins, int amount) {
  4.     int[] dp = new int[amount + 1];
  5.     // 数组大小为 amount + 1，初始值也为 amount + 1
  6.     Arrays.fill(dp, amount + 1);
  8.     // base case
  9.     dp[0] = 0;
  10.     // 外层 for 循环在遍历所有状态的所有取值
  11.     for (int i = 0; i < dp.length; i++) {
  12.         // 内层 for 循环在求所有选择的最小值
  13.         for (int coin : coins) {
  14.             // 子问题无解，跳过
  15.             if (i - coin < 0) {
  16.                 continue;
  17.             }
  18.             dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
  19.         }
  20.     }
  21.     return (dp[amount] == amount + 1) ? -1 : dp[amount];
  22. }

image.png

上面这个图，是不是让你想起了递推的题目 fibo，上台阶

PS：为啥 dp 数组初始化为 amount + 1 呢，因为凑成 amount 金额的硬币数最多只可能等于 amount（全用 1 元面值的硬币），所以初始化为 amount + 1 就相当于初始化为正无穷，便于后续取最小值。为啥不直接初始化为 int 型的最大值 Integer.MAX_VALUE 呢？因为后面有 dp[i - coin] + 1，这就会导致整型溢出。

计算机解决问题其实没有任何奇技淫巧，它唯一的解决办法就是穷举。
数学的优美，在计算机里就很少体现了，计算机直接利用物理属性(CPU的强大)，开启计算模式
哐哐算，然后就没了。

所以，我们规定好方法，让计算机卖苦力就可以了。
当物理上限达到后，就是TLE，开始动动脑筋，进行优化改进算法，进而在规定时间内解决问题。

用空间换时间的思路，是降低时间复杂度的不二法门
这个思路在生活中，也很常见。比如，Chrome浏览器，别看他快，占用空间也超级多

练习每个题目和解法时，多往「状态」和「选择」上靠，才能对这套框架产生自己的理解，运用自如。

凑零钱问题, 第二部分

1、递归解法Recursive formulation

image.png
image.png
image.png
image.png

  1. // 代码如下，但这个写法不是很高效(加上记忆化就好了)
  3. int solve(int x) {
  4.     if (x < 0) return INF;  //INF代表一个无穷大的值
  5.     if (x == 0) return 0;
  7.     int best = INF;
  8.     for (auto c : coins){   //枚举可以使用的硬币 这是C++11的写法
  9.        best = min(best, solve(x-c)+1);
  10.     }
  12.     return best;
  13. }

2、有向图Directed graphs

image.png
image.png

记忆化memoization

image.png

  1. //下面就是加记忆化的写法
  2. //The time complexity of the algorithm is O(nk), 
  3. //where n is the target sum and k is the number of coins.
  5. //题目背景，凑够n元，最少需要几枚硬币
  6. int solve(int x) {
  7.     if (x < 0) return INF;
  8.     if (x == 0) return 0;
  10.     if (ready[x]) return value[x];
  12.     int best = INF;
  13.     for (auto c : coins) {
  14.        best = min(best, solve(x-c)+1);
  15.     }
  17.     value[x] = best;
  18.     ready[x] = true;
  20.     return best;
  21. }
  23. //这份代码，并不是模板，理解明白就行

image.png

  1. // 下面是循环的写法
  3. value[0] = 0;
  4. for (int x = 1; x <= n; x++) {     //枚举sum
  5.     value[x] = INF;
  6.     for (auto c : coins) {         //枚举硬币 
  7.        if (x-c >= 0) {
  8.            value[x] = min(value[x], value[x-c]+1);
  9.         } 
  10.     }
  11. }
  13. // 这份代码，并不是模板，理解明白就行
  14. // value[n]

image.png

When we solve a recursive problem that its sub-problems overlaps(重叠), hence calling sub-problems. More than once and repeating its calculation in nature that typically makes the order exponentials!

When the original space is small enough to be memorized, then saving these sub-problems makes order small too, as sub-problems calculated once.

General Rules:
1- Recursive Function
2- Sub-calls Overlap
3- Small Search Space, so putting in memory is doable

加记忆化的例子，【Luogu P5017】Noip2018-T3 摆渡车题解

接下来加记忆化。其实在写记忆化搜索的时候，我个人认为加记忆化是最简单的，只要爆搜写好并且写对，加记忆化易如反掌。哪里有 return ，哪里加记忆化。最后代码如下（由于其余部分相同，这里只给出 dfs 代码）

加记忆化的例子，聊聊动态规划与记忆化搜索【特别经典】

  • 不依赖任何 外部变量
  • 答案以返回值的形式存在, 而不能以参数的形式存在(就是不能将 dfs 定义成 dfs(pos ,tleft , nowans ), 这里面的 nowans 不符合要求).
  • 对于相同一组参数, dfs 返回值总是相同的

加记忆化方法总结：

  1. 写出这道题的暴搜程序(最好是dfs)
  2. 将这个dfs改成”无需外部变量”的dfs
  3. 添加记忆化数组

“道法术”，改成无需外部变量，这些都是”术”层面的东西，当做一个新的角度来理解，是好的。不可从这个角度去死记硬背，因为这不是根源。

DP need good recursive mentality, that views answer in term of recursion!
So develop your skills!

Many DPs follow a certain pattern (style), we will investigate some of them.

最优子结构详解

「最优子结构」是某些问题的一种特定性质，并不是动态规划问题专有的。也就是说，很多问题其实都具有最优子结构，只是其中大部分不具有重叠子问题，所以我们不把它们归为动态规划系列问题而已。

我先举个很容易理解的例子：假设你们学校有 10 个班，你已经计算出了每个班的最高考试成绩。那么现在我要求你计算全校最高的成绩，你会不会算？当然会，而且你不用重新遍历全校学生的分数进行比较，而是只要在这 10 个最高成绩中取最大的就是全校的最高成绩。

我给你提出的这个问题就符合最优子结构：可以从子问题的最优结果推出更大规模问题的最优结果。让你算每个班的最优成绩就是子问题，你知道所有子问题的答案后，就可以借此推出全校学生的最优成绩这个规模更大的问题的答案。

你看，这么简单的问题都有最优子结构性质，只是因为显然没有重叠子问题，所以我们简单地求最值肯定用不出动态规划。

再举个常见但也十分简单的例子，求一棵二叉树的最大值，不难吧（简单起见，假设节点中的值都是非负数）：

  1. int maxVal(TreeNode root) {
  2.     if (root == null)
  3.         return -1;
  4.     int left = maxVal(root.left);
  5.     int right = maxVal(root.right);
  6.     return max(root.val, left, right);
  7. }

你看这个问题也符合最优子结构，以 root 为根的树的最大值，可以通过两边子树（子问题）的最大值推导出来，结合刚才学校和班级的例子，很容易理解吧。

当然这也不是动态规划问题，旨在说明，最优子结构并不是动态规划独有的一种性质，能求最值的问题大部分都具有这个性质；但反过来，最优子结构性质作为动态规划问题的必要条件，一定是让你求最值的，以后碰到那种恶心人的最值题，思路往动态规划想就对了，这就是套路。

动态规划不就是从最简单的 base case 往后推导吗，可以想象成一个链式反应，不断以小博大。但只有符合最优子结构的问题，才有发生这种链式反应的性质。(这里的链式反应，就是在描绘DAG)

找最优子结构的过程，其实就是证明状态转移方程正确性的过程，方程符合最优子结构就可以写暴力解了，写出暴力解就可以看出有没有重叠子问题了，有则优化，无则 OK。这也是套路，经常刷题的朋友应该能体会。

DP数组的遍历方向

做动态规划问题时，肯定会对DP数组的遍历顺序有些头疼。我们拿二维数组来举例，有时候我们是正向遍历

  1. int dp[N][N];
  2. for (int i = 0; i < m; i++)
  3.     for (int j = 0; j < n; j++)
  4.         // 计算 dp[i][j]

有时候我们反向遍历：

  1. for (int i = m - 1; i >= 0; i--)
  2.     for (int j = n - 1; j >= 0; j--)
  3.         // 计算 dp[i][j]

有时候可能会斜向遍历：

  1. // 斜着遍历数组
  2. for (int l = 2; l <= n; l++) {
  3.     for (int i = 0; i <= n - l; i++) {
  4.         int j = l + i - 1;
  5.         // 计算 dp[i][j]
  6.     }
  7. }

那么，如果仔细观察的话可以发现其中的原因的。你只要把住两点就行了：
1、遍历的过程中，所需的状态必须是已经计算出来的。
2、遍历的终点必须是存储结果的那个位置。

下面来具体解释上面两个原则是什么意思。

比如编辑距离这个经典的问题，edit distance编辑距离，我们通过对dp数组的定义，确定了 base case 是dp[..][0]和dp[0][..]，最终答案是dp[m][n]；

而且我们通过状态转移方程知道dp[i][j]需要从dp[i-1][j], dp[i][j-1], dp[i-1][j-1]转移而来，如下图：

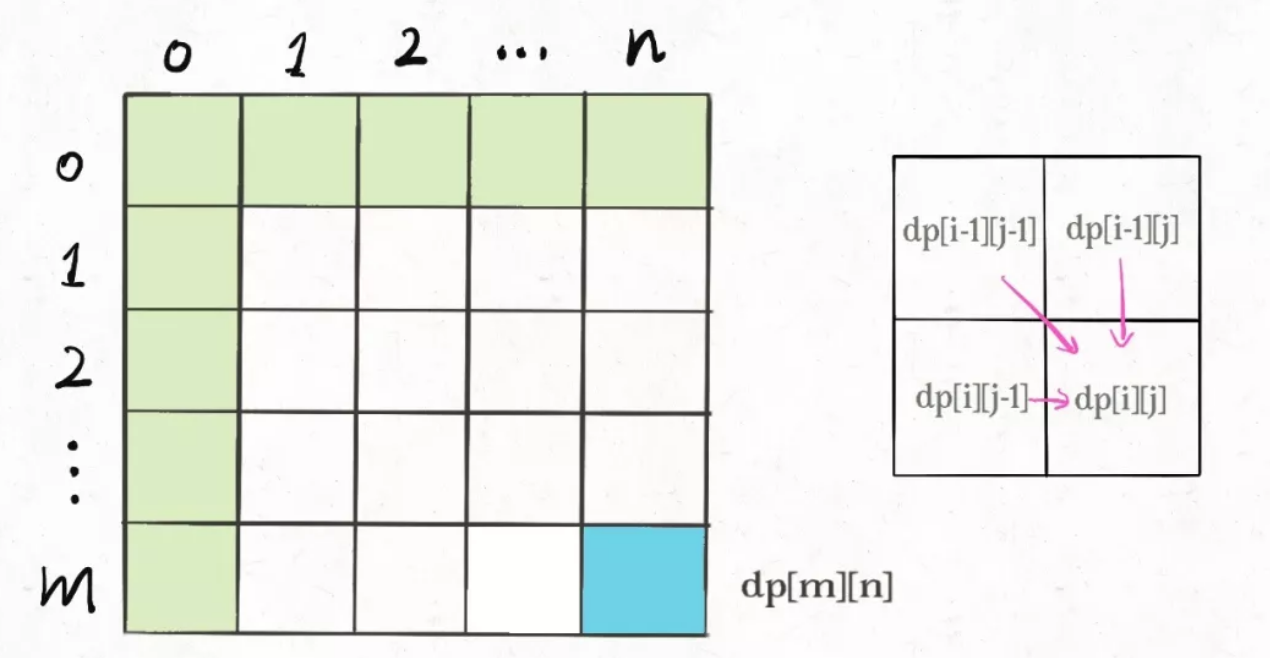
image.png

那么，参考刚才说的两条原则，你该怎么遍历dp数组？肯定是正向遍历：

  1. for (int i = 1; i < m; i++)
  2.     for (int j = 1; j < n; j++)
  3.         // 通过 dp[i-1][j], dp[i][j-1], dp[i-1][j-1]
  4.         // 计算 dp[i][j]

因为，这样每一步迭代的左边、上边、左上边的位置都是 base case 或者之前计算过的，而且最终结束在我们想要的答案dp[m][n]。

现在，你应该理解了这两个原则，主要就是看 base case 和最终结果的存储位置，保证遍历过程中使用的数据都是计算完毕的就行，有时候确实存在多种方法可以得到正确答案，可根据个人口味自行选择。

关于遍历顺序，需要结合实际情况分析 比如，在01背包中，正向和反向的意义完全不同，这是理解的核心 上文这段对遍历顺序的描述，其本质，就是状态转移方程的设计

参考：#手把手刷动态规划

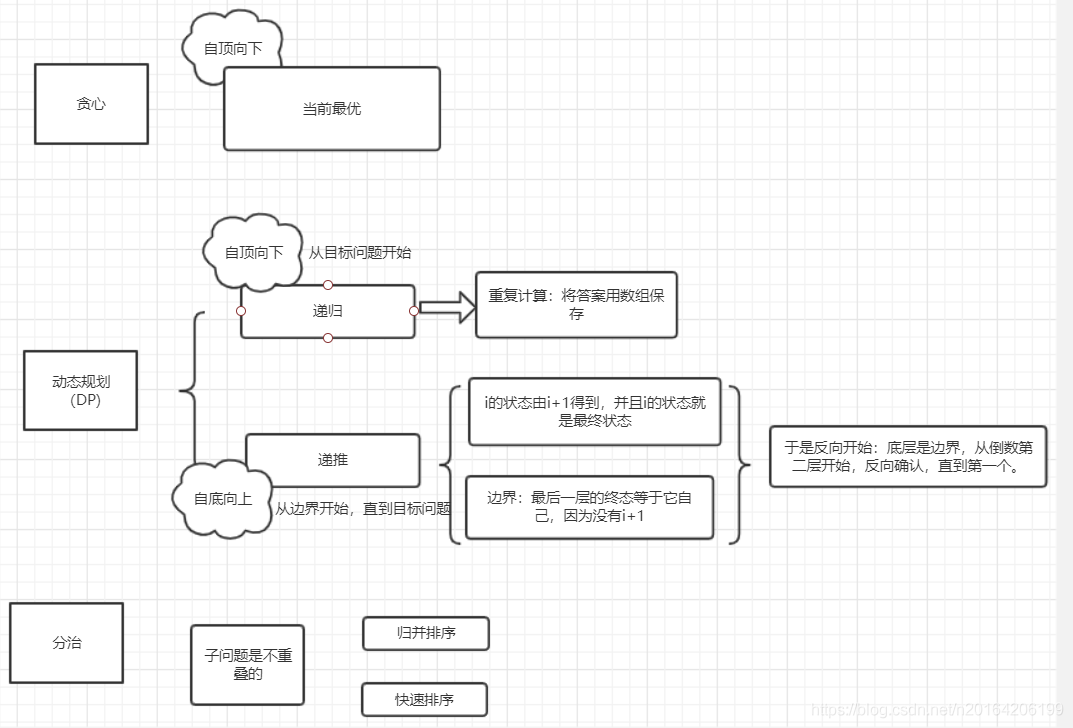
DP与贪心

贪心算法的策略是每次取最大值，但并不是每一次都有效。我们下面看看，

反例，
背包体积是10，有三个物品
体积9，价值100
体积3，价值60
体积7，价值70

如果是贪心，贪心思路是优先选价值大的，会选择100的，占用9体积，就不能选其他了
如果是dp，选择体积是3+7的方案，获得价值130

DP与分治

Do we need to apply DP for merge sort? NEVER, a call will never be repeated! like most of Divide-and-Conquer Algorithm.

分治与dp，两者都是将问题划分为子问题，然后求解子问题。
当子问题不会被求解多次的时候，应该用分治；被求解多次的，就dp。
例如，二叉查找，用分治；求fibo，用dp。

Dynamic Programming most typical cases: Minimization, Maximization and Counting. But could have adhock usages. In fact, above code is not called DP, it is call Memoization (NOT Memorization). It is a technique when we have a recusive function and save calls).

DP is to build bottom up according to recurrence while Memoization is top-down.

  1. int dp_fib(int n)
  2. {
  3.     int fib[MAX];
  4.     fib[0] = fib[1] = 1;    // base case
  6.     for(int i = 2; i <= n; ++i)
  7.         fib[i] = fib[i-1] + fib[i-2];    // bottom up according to recurrence
  9.     return fib[n];
  10. }

image.png

Writing Memoization is much more natural, although there are cases when DP is a must.

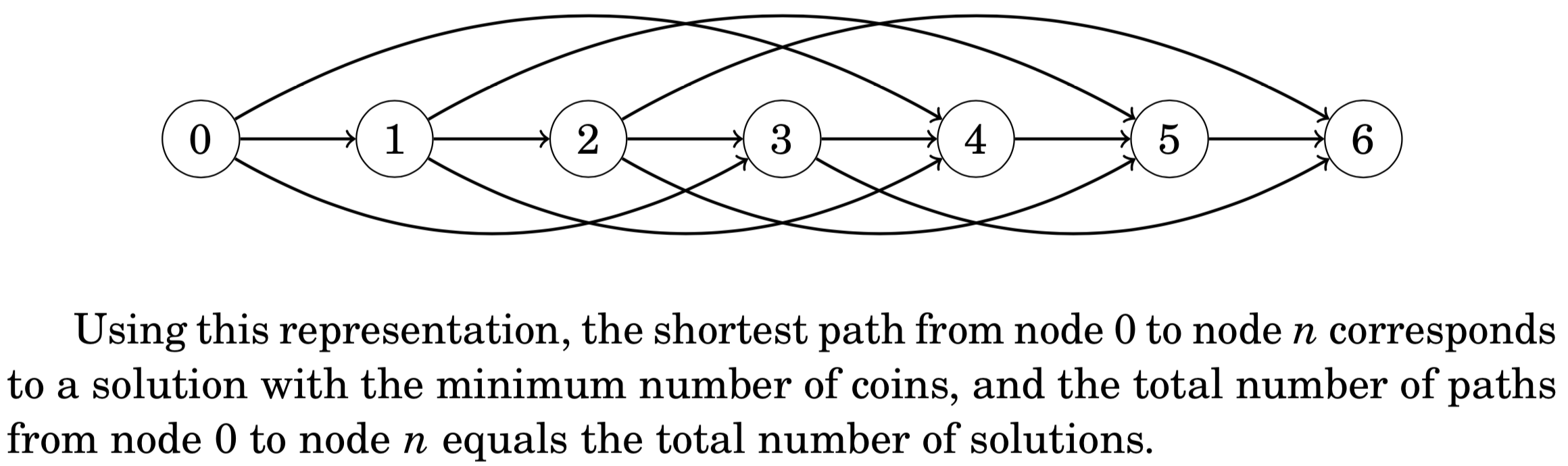
打印方案Constructing a solution

image.png
dp问题当中，有很多情况，不仅让你求最值，还让你输出最值情况下的方案是什么（如果有多种方案，输出一种即可，oj会做special judge）

  1. //we can declare another array that indicates for each sum of money 
  2. //the first coin in an optimal solution:
  4. value[0] = 0;
  5. for (int x = 1; x <= n; x++) {      //枚举体积
  6.     value[x] = INF;
  7.     for (auto c : coins) {          //枚举硬币
  8.        if (x-c >= 0 && value[x-c]+1 < value[x]) {
  9.            value[x] = value[x-c]+1;
  10.            first[x] = c;
  11.         }
  12.     }
  13. }
  15. // 循环输出方案
  16. while (n > 0) {
  17.     cout << first[n] << "\n";
  18.     n -= first[n];
  19. }
  1. // 完整代码
  2. #include <iostream>
  4. using namespace std;
  6. int n, m, a[15];
  7. int value[15];
  8. int first[15];
  10. int main()
  11. {
  12.     memset(value, 0x3f, sizeof value);
  14.     cin >> n >> m;
  15.     for (int i = 1; i <= n; i++) cin >> a[i];
  17.     value[0] = 0;
  18.     for (int x = 1; x <= m; x++){            //枚举体积
  19.         for (int i = 1; i <= n; i++)         //枚举硬币
  20.             if (x - a[i] >= 0 && value[x - a[i]] + 1 < value[x]){
  21.                 value[x] = value[x - a[i]] + 1;
  22.                 first[x] = a[i];            //记录方案
  23.             }
  24.     }
  26.     int sum = m;
  27.     while (sum > 0){
  28.         cout << first[sum] << ' ';
  29.         sum -= first[sum];
  30.     }
  31.     puts("");
  33.     return 0;
  34. }
  36. /*
  37. 3 10
  38. 1 3 4
  39. */

输出方案，我们更多的，还可以用递归输出方案

  1. // 递归输出方案
  2. void print(int x)
  3. {
  4.     if (x == 0) return ;
  5.     printf("%d ", first[x]); //这两行的顺序，决定了先递归再输出当前，还是先输出当前，再递归
  6.     print(x - first[x]);
  7. }
  9. int main()
  10. {
  11.     //..........
  13.     print(10);
  14.     puts("");
  16.     return 0;
  17. }
  1. // 完整代码
  2. #include <iostream>
  4. using namespace std;
  6. int n, m, a[15];
  7. int value[15];
  8. int first[15];
  10. void print(int x)
  11. {
  12.     if (x == 0) return ;
  13.     printf("%d ", first[x]);
  14.     print(x - first[x]);
  15. }
  17. int main()
  18. {
  19.     memset(value, 0x3f, sizeof value);
  21.     cin >> n >> m;
  22.     for (int i = 1; i <= n; i++) cin >> a[i];
  24.     value[0] = 0;
  25.     for (int x = 1; x <= m; x++){            // 枚举体积
  26.         for (int i = 1; i <= n; i++)         // 枚举硬币
  27.             if (x - a[i] >= 0 && value[x - a[i]] + 1 < value[x]){
  28.                 value[x] = value[x - a[i]] + 1;
  29.                 first[x] = a[i];             // 记录方案
  30.             }
  31.     }
  33.     print(m);
  34.     puts("");
  36.     return 0;
  37. }
  39. /*
  40. 3 10
  41. 1 3 4
  42. */

统计方案数Counting the number of solutions

image.png
image.png

  1. count[0] = 1;
  2. for (int x = 1; x <= n; x++) {     //枚举sum
  3.     for (auto c : coins) {         //枚举硬币
  4.        if (x-c >= 0) {
  5.            count[x] += count[x-c];
  6.            //count[x] %= m;
  7.        }
  8.     } 
  9. }

image.png

  1. #include <iostream>
  3. using namespace std;
  5. int n, m, a[15];
  6. int value[15];
  7. int cnt[15];
  9. int main()
  10. {
  11.     memset(value, 0x3f, sizeof value);
  13.     cin >> n >> m;
  14.     for (int i = 1; i <= n; i++) cin >> a[i];
  16.     cnt[0] = 1;                              //体积为0有一种方案
  17.     for (int x = 1; x <= m; x++){            //枚举sum，从小到大枚举
  18.         for (int i = 1; i <= n; i++)         //枚举硬币
  19.             if (x - a[i] >= 0){
  20.                 cnt[x] += cnt[x - a[i]];
  21.             }
  22.     }
  24.     cout << cnt[m] << '\n';
  26.     return 0;
  27. }
  29. /*
  30. 输入
  31. 3 5
  32. 1 3 4
  35. 输出
  36. 6
  37. */

Now we have discussed all basic ideas of dynamic programming.

《一本通》清单

【例9.2】数字金字塔
  1. //数字三角形模型

【例9.3】求最长不下降序列
  1. //LIS

【例9.4】拦截导弹(Noip1999)
  1. //LIS

【例9.5】城市交通路网
  1. //LIS

【例9.6】挖地雷
  1. //LIS

【例9.7】友好城市
  1. //LIS

【例9.8】合唱队形
  1. //LIS

【例9.9】最长公共子序列
  1. //LCS

【例9.10】机器分配
  1. //dp[i][j]前i个公司，分配j台设备的最大价值
  2. //递归打印方案，这个输出方案的方案，需要多学习

最长上升子序列
  1. //LIS

最大子矩阵
  1. //最大子段和 + 前缀和，O(n^3)

登山
  1. //LIS

摘花生
  1. //数字三角形模型

最大上升子序列和
  1. //LIS

怪盗基德的滑翔翼
  1. //LIS

最低通行费
  1. //LIS

三角形最佳路径问题
  1. //数字三角形模型

拦截导弹
  1. //LIS
  2. //如果要拦截所有导弹最少要配备多少套这种导弹拦截系统

【例9.11】01背包问题
  1. //01背包

【例9.12】完全背包问题
  1. //完全背包

【例9.13】庆功会
  1. //多重背包

【例9.14】混合背包
  1. //混合背包

【例9.15】潜水员
  1. //这个题目注意一个瓶子里的氧气和氮气，不是完整的用，可以只用一部分从而满足工作需要。

https://www.acwing.com/solution/content/7438/

背包问题中 体积至多是 j ，恰好是 j ，至少是 j 的初始化问题的研究

【例9.16】分组背包
  1. //分组背包，每组里只能选一个物品

【例9.17】货币系统
  1. //完全背包，求方案数

采药
  1. //01背包，noip原题

数字组合
  1. //01背包，求方案数

宠物小精灵之收服
  1. //小智的精灵球数量和皮卡丘的初始体力
  2. //二维费用背包
  3. //输出，收服C个小精灵时皮卡丘的剩余体力值最多为R。这个最后输出剩余体力值的方法也很聪明

买书
  1. //完全背包，求方案数
  2. //和 数字组合 ，比较像

Charm Bracelet
  1. //01背包

装箱问题
  1. //任取若干个装入箱内，使箱子的剩余空间为最小
  2. //01背包，输出V-dp[V]

开餐馆
  1. //LIS模型，i接在1..i-1谁后面的时候，注意判断距离问题

【例9.18】合并石子
  1. //区间dp

【例9.19】乘积最大
  1. //int dp[N][M]; //前i个数，插入了j个乘号
  2. //先预处理出来数字的问题，更好一些

https://www.acwing.com/solution/content/18940/

【例9.20】编辑距离
  1. //编辑距离，经典问题

【例9.21】方格取数
  1. //从左上走到右下，走了两次，问能取到的最大值
  2. //定义一个四维的状态，dp[N][N][N][N]，经过发现，可以优化到三维

【例9.22】复制书稿(book)
  1. //输出具体方案，用了一个贪心的策略去设计输出答案的过程
  2. //以下两种设计都可行，请体验体验
  3. //设计状态dp[i][j] i个人，抄前j本书的复制时间
  4. //设计状态dp[i][j] i个本书，有前j个人去抄

【例9.23】橱窗布置(flower)
  1. //dp[i][j] 前i朵花插在前j个花瓶里

【例9.24】滑雪
  1. //记忆化

公共子序列
  1. //LCS

计算字符串距离
  1. //编辑距离

糖果
  1. //《1195：判断整除》这道递推类似，请回忆。

鸡蛋的硬度
  1. //特别经典的一道题目，很难的，基本自己想不出来的，可以思考二十分钟试一试
  2. //有两种设计状态的方法
  3. //dp[i][j] 测量长度i层楼，用j个鸡蛋，最坏情况下需要扔的次数，O(n^2*m)
  4. //dp[i][j] 用j个鸡蛋测i次，最多能测量的区间长度，O(nm)

大盗阿福
  1. //从一个商店，可以被盗，也可以不被盗的两种情况入手，思考状态的设计dp[N][2]
  2. //还有一种思路，线性dp的思路，状态只有一维，类似最大字段和的O(n)操作

股票买卖
  1. //dp，状态机模型
  2. //ybt的第8个测试点，跑起来不稳定，有可能会TLE这个点
  3. //dp[N][3][2]; //dp(i,j,0)第i天，买卖j次，当前没有股票；dp(i,j,1)当前有股票

鸣人的影分身
  1. //分苹果->鸣人的影分身->数的划分
  2. //本题可以从分苹果入手，实现记忆化搜索的版本
  3. //然后，再改成循环版本
  4. //最后，再重新的，从集合角度出发，分析 (最小值为0 | 最小值不为0) 的推导过程

数的划分
  1. //先从鸣人的影分身，变形一下，实现第一个版本，trick一下就可以
  2. //重新的，从集合角度出发，分析(.... | .....)

Maximum sum
  1. //这段题目求的是，两个不重合的最大子段和
  2. //最大子段和，这个会写的
  3. //如何表示两个不重合的最大子段和呢？ 多画图看一看就会找到线索

最长公共子上升序列
  1. //LIS+LCS，非常好的题目，这个题面还要求输出方案。
  2. //有O(n^4), O(n^3), O(n^2)的写法，都需要深入思考，琢磨实现

[

](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzAxODQxMDM0Mw==&action=getalbum&album_id=1318881141113536512&scene=173&from_msgid=2247491172&from_itemidx=1&count=3&nolastread=1#wechat_redirect)