backtracking回溯

回溯法是一种经常被用在深度深度优先搜索（DFS）和广度优先搜索（BFS）的技巧。其本质是：走不通就回头。关键词：恢复现场。

例题:八皇后问题

As an example, consider the problem of calculating the number of ways n queens can be placed on an n × n chessboard so that no two queens attack each other. For example, when n = 4, there are two possible solutions: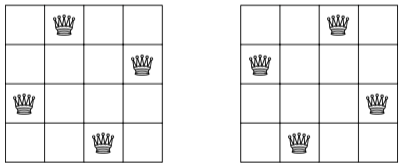

The problem can be solved using backtracking by placing queens to the board row by row. More precisely, exactly one queen will be placed on each row so that no queen attacks any of the queens placed before. A solution has been found when all n queens have been placed on the board.

For example, when n = 4, some partial solutions generated by the backtracking algorithm are as follows: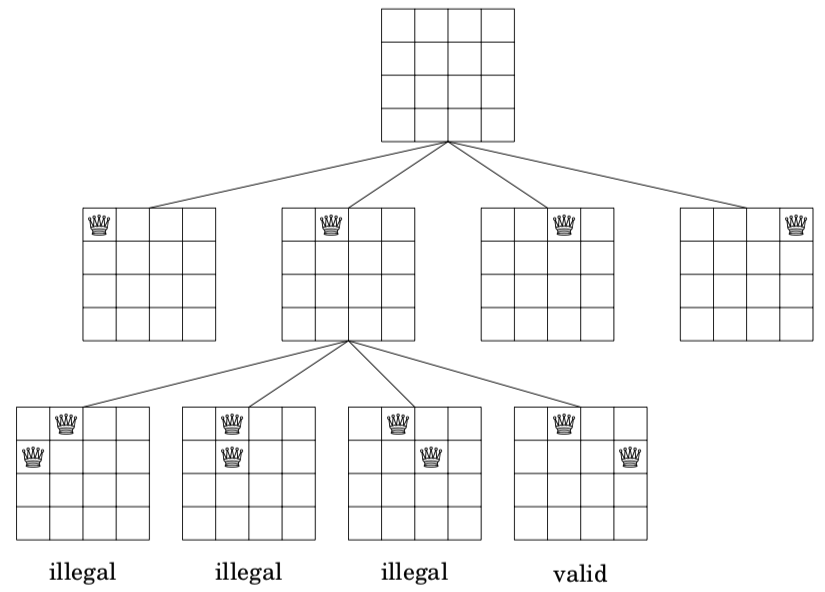

At the bottom level, the three first configurations are illegal, because the queens attack each other. However, the fourth configuration is valid and it can be extended to a complete solution by placing two more queens to the board. There is only one way to place the two remaining queens.

void search(int y) {
    if (y == n) {
        count++;
        return; 
    }
    for (int x = 0; x < n; x++) {
        if (column[x] || diag1[x+y] || diag2[x-y+n-1]) continue;
        column[x] = diag1[x+y] = diag2[x-y+n-1] = 1;
        search(y+1);
        column[x] = diag1[x+y] = diag2[x-y+n-1] = 0;
    }
}
search(0); //调用

Let denote the number of ways to place n queens on an n × n chessboard. The above backtracking algorithm tells us that, for example, 。（记住：八皇后问题有92种方案）

// 按行枚举
//（1）反对角线 y=x+b, 截距 b=y−x，因为我们要把 b 当做数组下标，所以 b 不能是负的
// 所以我们 +n，保证是结果是正的
//（2）而对角线 y=−x+b, 截距是 b=y+x，这里截距一定是正的，所以不需要加偏移量
// 反对角线，左上到右下
// 对角线，左下到右上
// 反对角线udg[n−u+i]，对角线 dg[u+i]中的下标
// n−u+i，u+i 表示的是截距
#include <iostream>
using namespace std;
const int N = 20;
// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// g[N][N]用来存路径
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u)
{
    // u == n 表示已经搜了n行，故输出这条路径
    if (u == n)
    {
        for (int i = 0; i < n; i ++ ) puts(g[i]);   // 等价于cout << g[i] << endl;
        puts("");  // 换行
        return;
    }
    //对n个位置按行搜索
    for (int i = 0; i < n; i ++ )
        //剪枝(对于不满足要求的点，不再继续往下搜索)
        //udg[n - u + i]，+n是为了保证大于0
        if (!col[i] && !dg[u + i] && !udg[n - u + i])
        {
            g[u][i] = 'Q';
            col[i] = dg[u + i] = udg[n - u + i] = true;
            dfs(u + 1);
            // 恢复现场 这步很关键
            col[i] = dg[u + i] = udg[n - u + i] = false;
            g[u][i] = '.';
        }
}
int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';
    dfs(0);
    return 0;
}

// 按每个元素进行枚举
#include <iostream>
using namespace std;
const int N = 20;
// 因为是一个个搜索，所以加了row
int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N];
// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{
    // 处理超出边界的情况
    if (y == n) y = 0, x ++ ;
    // 说明已经放好了n个皇后，表示枚举完 n^2 个了
    if (x == n)
    {
        if (s == n)
        {
            for (int i = 0; i < n; i ++ ) puts(g[i]);
            puts("");
        }
        return;
    }
    // 不放皇后  就往下搜下一个位置
    dfs(x, y + 1, s);
    // 放皇后
    if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n])
    {
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
        dfs(x, y + 1, s + 1);
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
        g[x][y] = '.';
    }
}
int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';
    dfs(0, 0, 0);
    return 0;
}

参考https://www.acwing.com/solution/content/2820/